л4_27 Функции

1.

Дисциплина «МАТЕМАТИКА»
Тема 4. Введение в математический анализ
Занятие 27. Функции

2.

Результаты текущей успеваемости 1 года обучения
за сентябрь месяц
Шипачев В.С. «Высшая математика», М.: «Высшая
школа», 2005 – 479 с. – С. 69-73.

3.

Результаты текущей успеваемости 1 года обучения
за сентябрь месяц
1. Функция, ее область определения и множество
значений. Сложная функция.
2. Способы задания функций.
3. Основные элементарные функции, их свойства,
графики.

4.

Количество
проведенных
1. Функция,
ее область
определения и
контрольных проверок
множество значений. Сложная функция
«функция»
(от латинского functio совершение, выполнение)
Впервые употреблено в 1673 г.
Функция – «отрезок, длина
которого меняется по какомунибудь определенному закону»
Готфрид Вильгельм
Лейбниц
(1646-1716)
немецкий философ,
математик, физик

5.

Количество
проведенных
1. Функция,
ее область
определения и
контрольных проверок
множество значений. Сложная функция
«функцией переменной
величины называют количество,
образованное каким угодно
способом из этой переменной
величины и постоянных»
Иоганн Бернулли
(1677-1748)
швейцарский математик

6.

Количество
проведенных
1. Функция,
ее область
определения и
контрольных проверок
множество значений. Сложная функция
«Функция переменного
количества есть аналитическое
выражение, составленное
каким-либо образом из этого
количества и чисел или
постоянных количеств»
Леонард Эйлер
(1707-1783)
математик, физик,
механик и астроном
Обозначение:
(x)

7.

Количество
проведенных
1. Функция,
ее область
определения и
проверок функция
множество контрольных
значений. Сложная
Пусть X = {x} - числовое множество.
Определение.
Если каждому значению переменной x Є X
поставлено в соответствие по некоторому
правилу одно определенное значение
другой переменной y, то y есть функция
от переменной x.
Обозначение:
y=f(x).

8.

Количество
проведенных
1. Функция,
ее область
определения и
проверок функция
множество контрольных
значений. Сложная
Определение.
Совокупность всех значений аргумента, при
которых соответствующее значение функции
выражается действительным числом, называется
областью существования или областью
определения функции.
Обозначение:
D(f)

9.

Количество
проведенных
1. Функция,
ее область
определения и
проверок функция
множество контрольных
значений. Сложная
Определение.
Графиком функции y=f(x) называется
множество всех точек плоскости (XOY),
абсциссами которых являются значения
аргумента x, а ординатами - соответствующие
значения y=f(x).

10.

Количество
проведенных
1. Функция,
ее область
определения и
проверок функция
множество контрольных
значений. Сложная
Определение.
Если y есть функция от u, т.е. y=f(u), а u, в
свою очередь, есть функция от x, т.е. u= (x),
то y=f( (x))
называется
сложной функцией
от x
(функцией от функции или суперпозицией функций).
y=cos3x,
y=cosu,
y=lnsin(x-2),
y=lnu,
u=3x;
u=sinv, v=x-2.

11.

Количество проведенных
2. Способы
задания
функций
контрольных
проверок
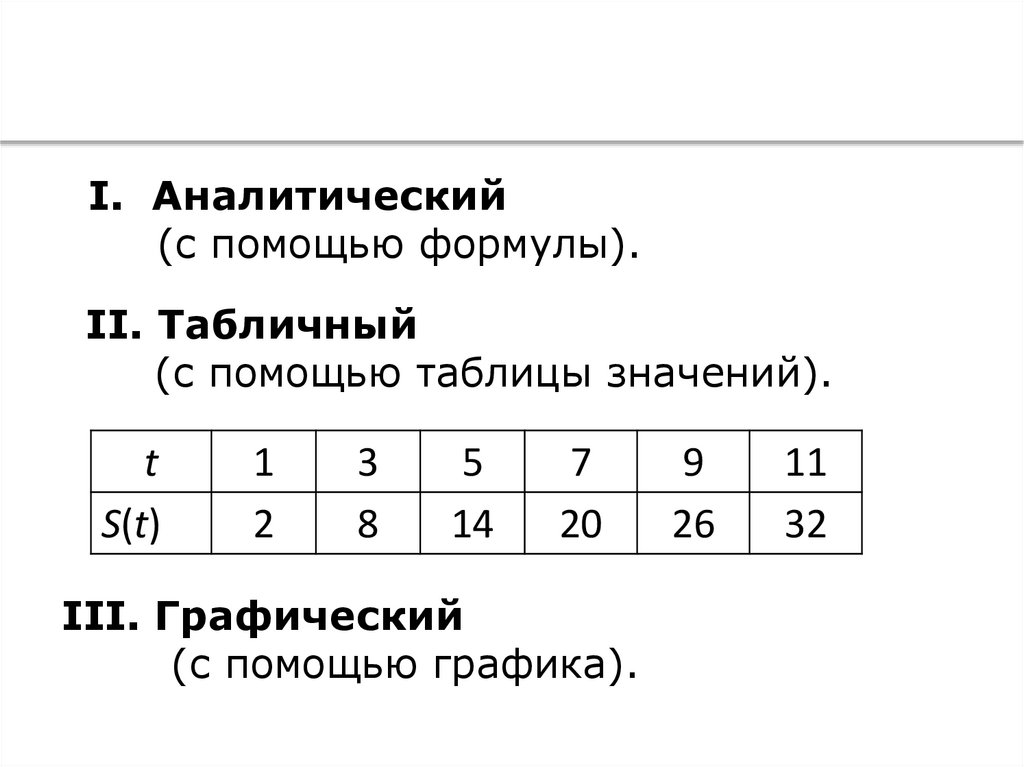
I. Аналитический
(с помощью формулы).
II. Табличный
(с помощью таблицы значений).
t
S(t)
1
2
3
8
5
14
7
20
III. Графический
(с помощью графика).
9
26
11
32

12.

Количество проведенных
3. Основные элементарные
контрольныхфункции,
проверок их свойства,
графики.
Основные элементарные функции:
а)
Степенная функция: у = х ,
где — действительное число.
б) Показательная функция: у = aх,
где основание степени
a —положительное число, a≠1.
в)
Логарифмическая функция: у = logax,
где основание логарифмов
a — положительное число, a≠1.

13.

Количество проведенных
контрольных проверок
Основные элементарные функции:
г) Тригонометрические функции:
y=sinx, y=cosx, y=tgx,
y=ctgx, y=secx, y=cosecx.
д) Обратные тригонометрические функции:
y=arcsin x,
y=arccos x, y=arctg x,
y=arcctg x,
y=arcsec x,
y=arccosecx.

14.

Количество проведенных
контрольных проверок
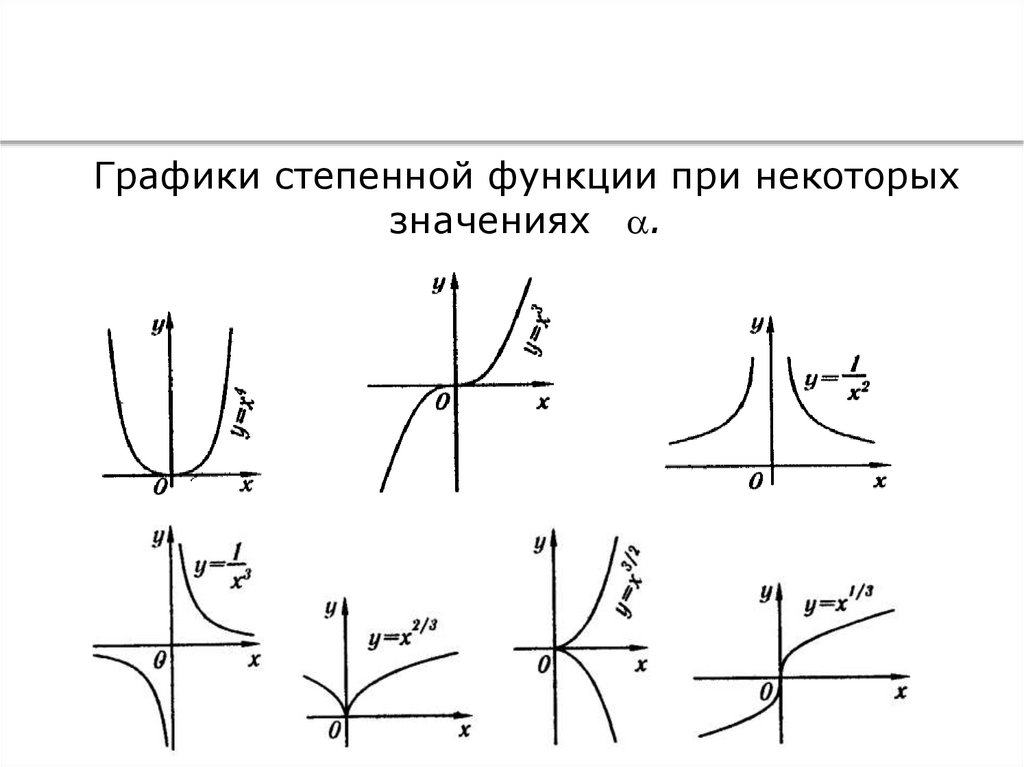
Графики степенной функции при некоторых
значениях .

15.

Количество проведенных
контрольных проверок
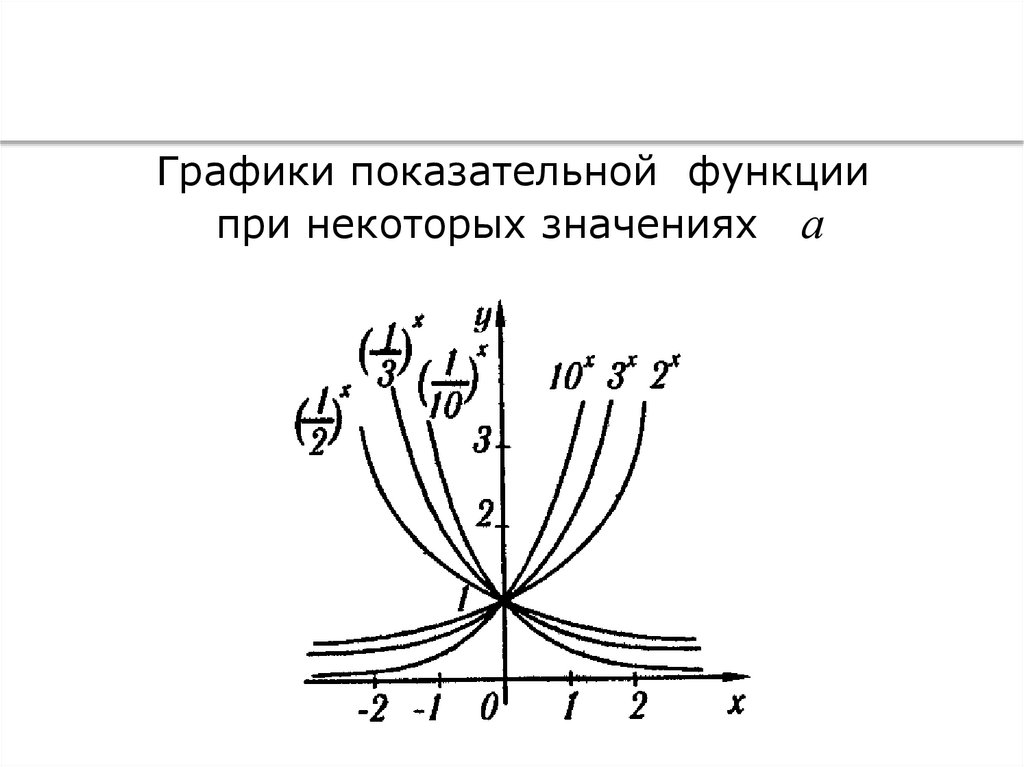
Графики показательной функции
при некоторых значениях а

16.

Количество проведенных
контрольных проверок
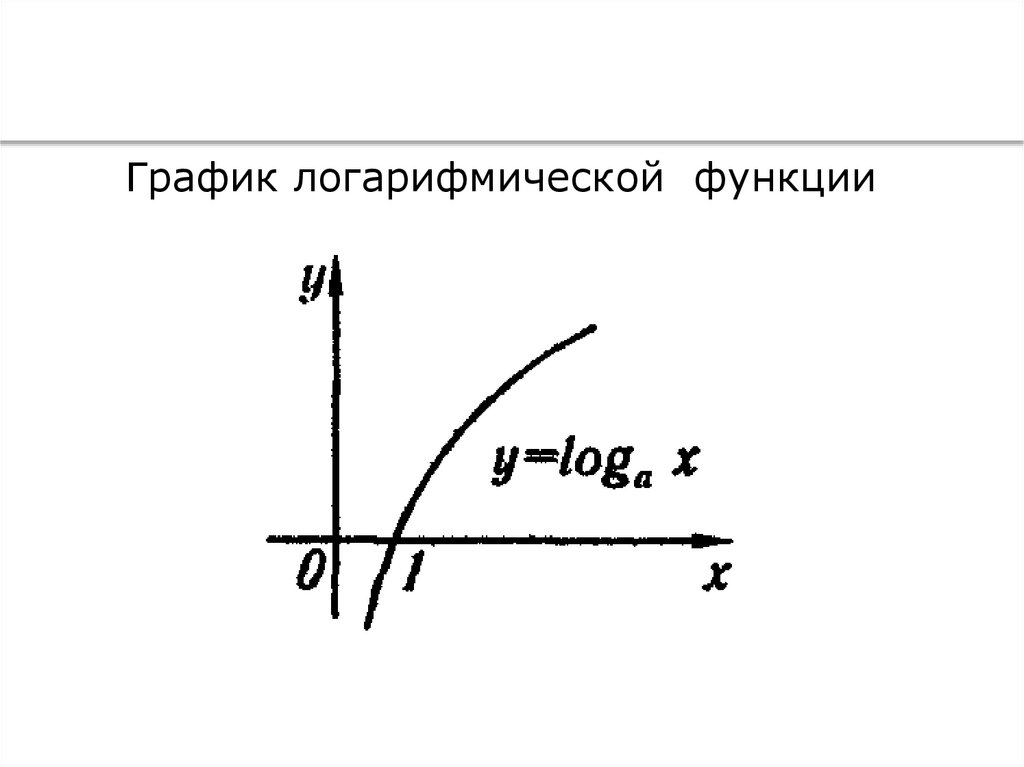
График логарифмической функции

17.

Количество проведенных
контрольных проверок
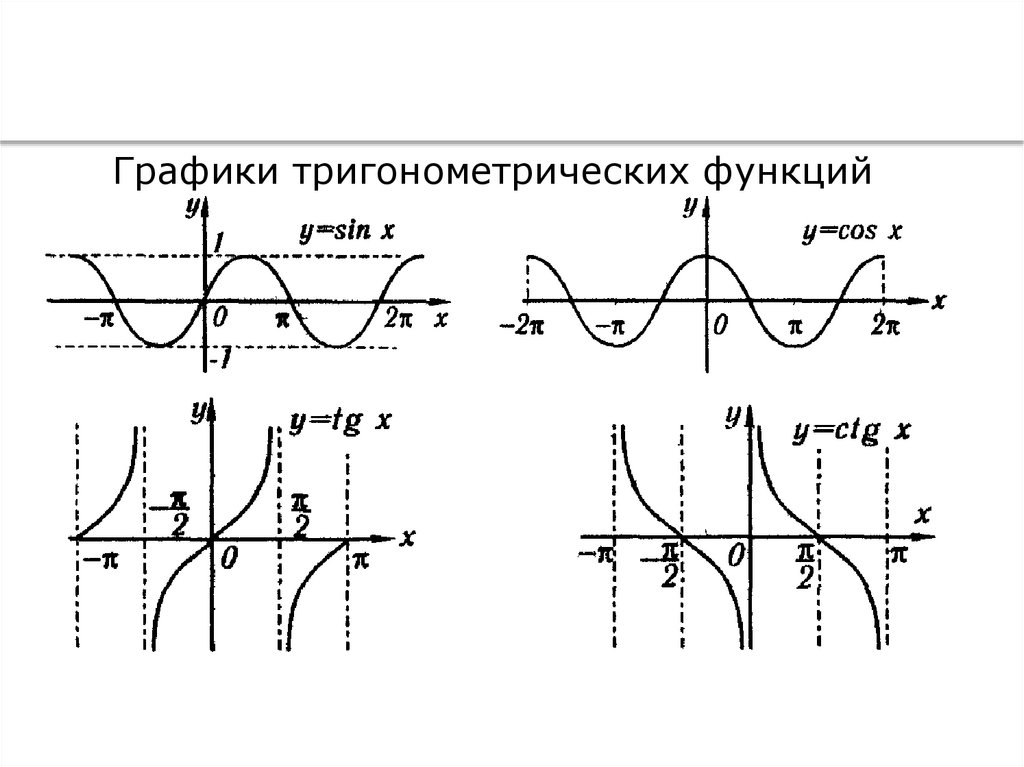
Графики тригонометрических функций

18.

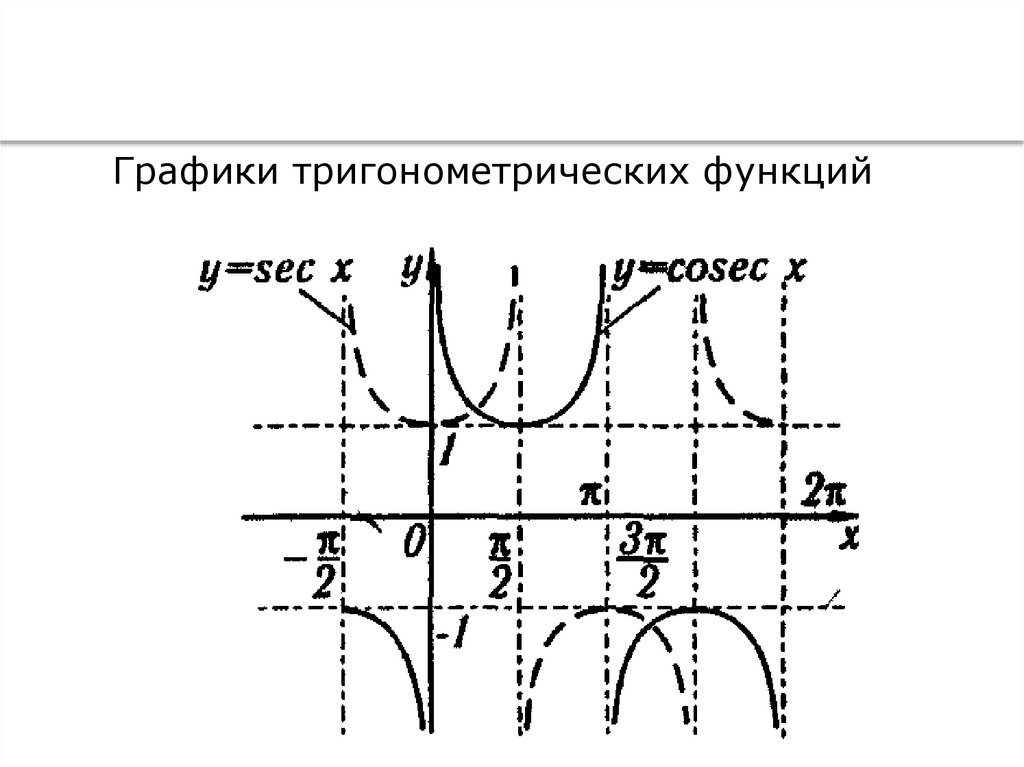
Количество проведенных
контрольных проверок
Графики тригонометрических функций

19.

Количество проведенных
контрольных проверок
Алгебраические функции
а). Целая рациональная функция
или многочлен
y a0 x
n
a1 x
n 1
... a n
б). Дробная рациональная функция
a 0 x n a 1 x n 1 ... a n
y
b 0 x m b 1 x m 1 ... b m

20.

Количество проведенных
контрольных проверок
Элементарные функции
Иррациональная функция
Примеры иррациональных функций:
y
2x x
2
1 5x 2
,
y x

21.

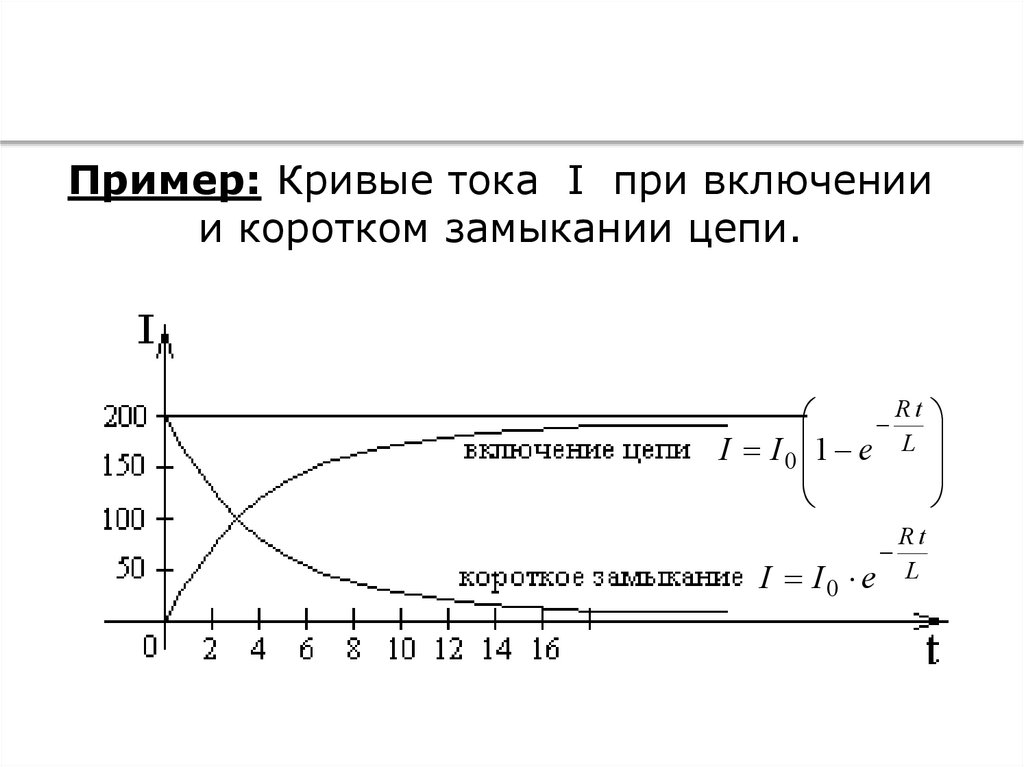
Количество проведенных
контрольных проверок
Пример: Кривые тока I при включении
и коротком замыкании цепи.
Rt
I I 0 1 e L
I I0 e
Rt
L

22.

Количество проведенных
Элементы
поведения
функции
контрольных
проверок
I. Четность, нечетность функции.
II. Периодичность функции.
III. Монотонность функции.
IV. Ограниченность функции.
V. Наибольшее и наименьшее значения
функции.
VI. Нули функции.