поверхности_концентр_сферы_лекция12

1. Пересечение поверхностей

Нажмите клавишу F5

2. Методы построения линии пересечения кривых поверхностей

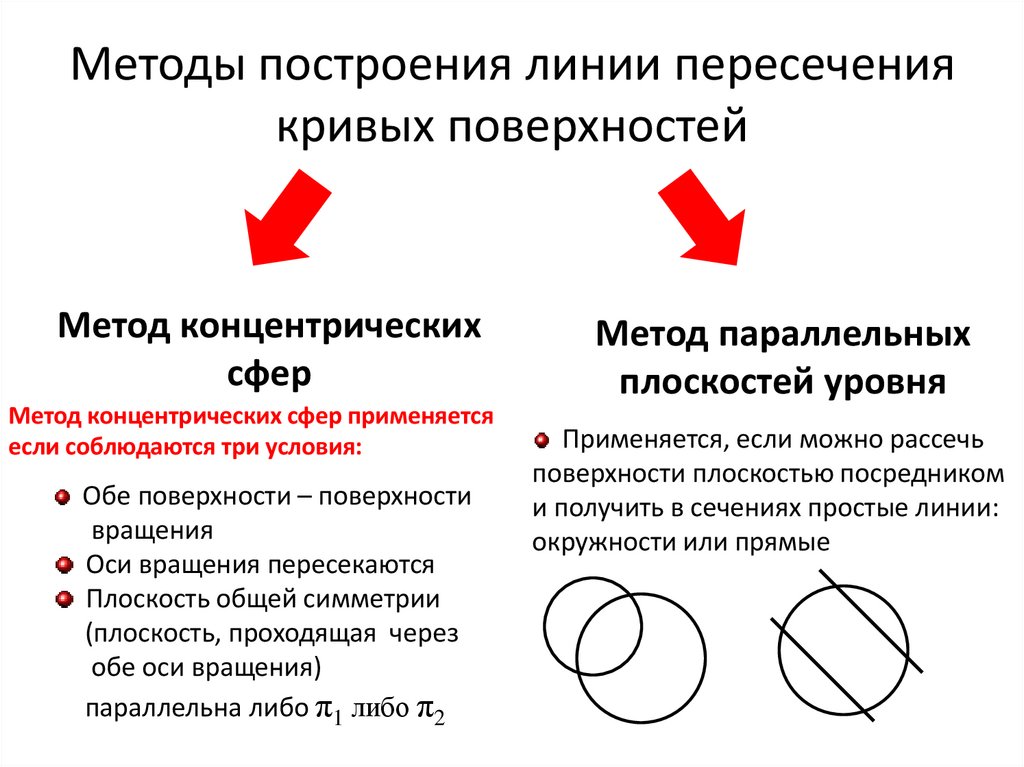
Метод концентрических
сфер
Метод концентрических сфер применяется
если соблюдаются три условия:
Обе поверхности – поверхности
вращения
Оси вращения пересекаются
Плоскость общей симметрии
(плоскость, проходящая через
обе оси вращения)
параллельна либо π1 либо π2
Метод параллельных
плоскостей уровня
Применяется, если можно рассечь
поверхности плоскостью посредником
и получить в сечениях простые линии:
окружности или прямые

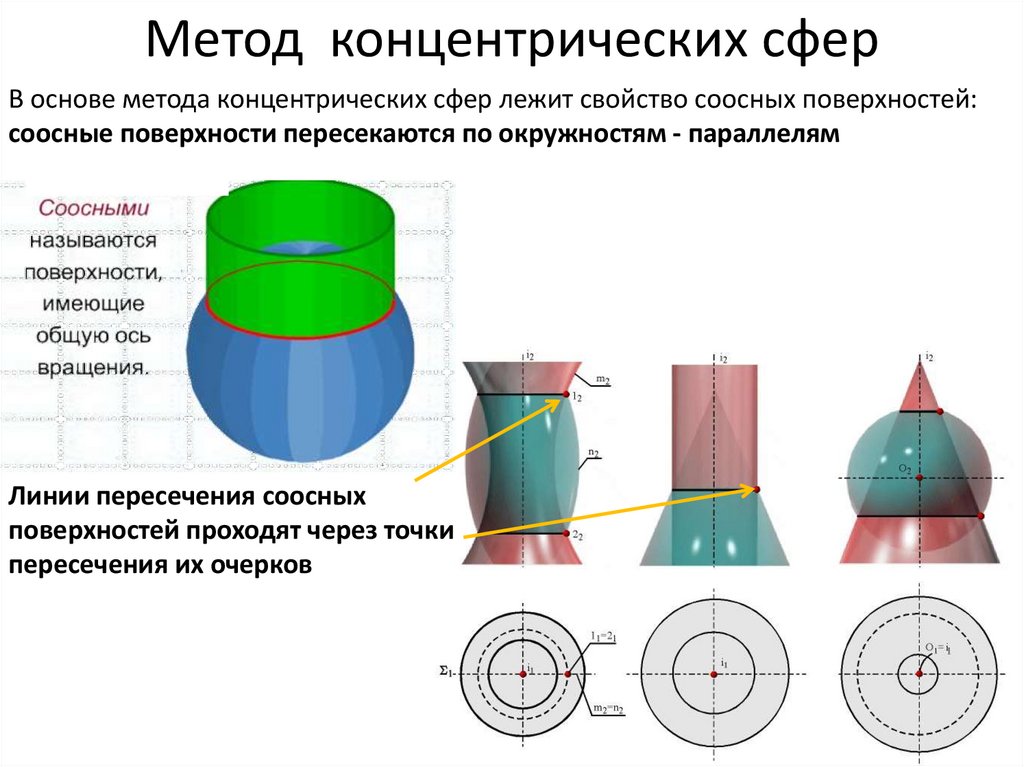
3. Метод концентрических сфер

В основе метода концентрических сфер лежит свойство соосных поверхностей:
соосные поверхности пересекаются по окружностям - параллелям
Линии пересечения соосных
поверхностей проходят через точки
пересечения их очерков

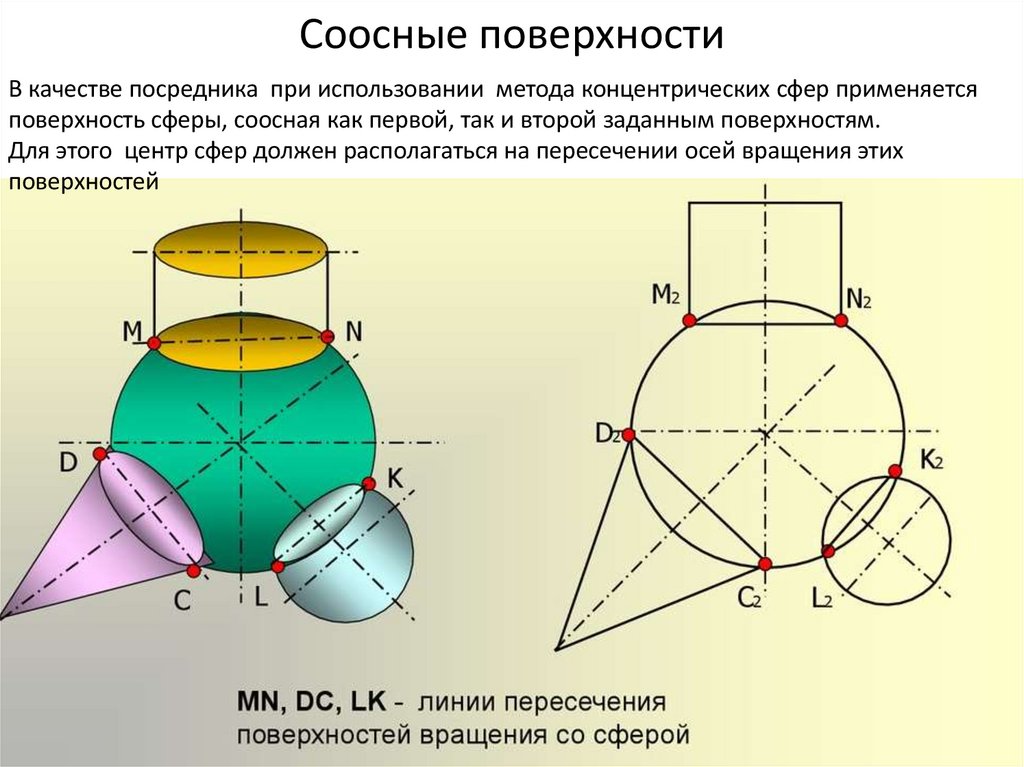
4. Соосные поверхности

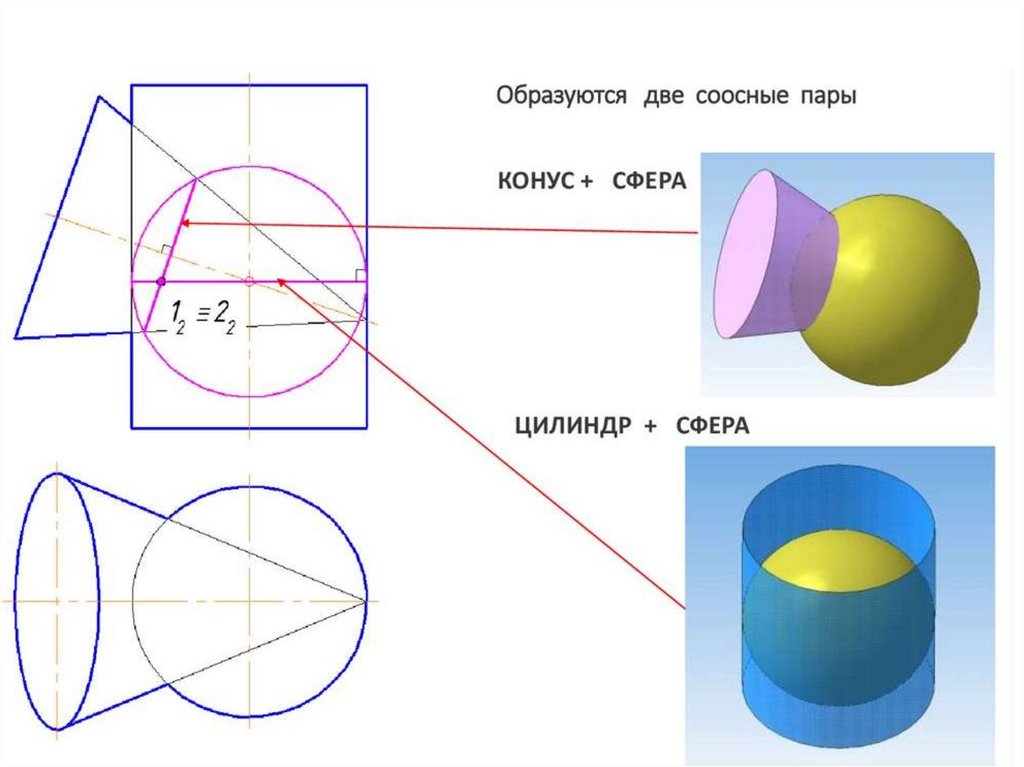
В качестве посредника при использовании метода концентрических сфер применяется
поверхность сферы, соосная как первой, так и второй заданным поверхностям.
Для этого центр сфер должен располагаться на пересечении осей вращения этих
поверхностей

5.

6. Метод концентрических сфер

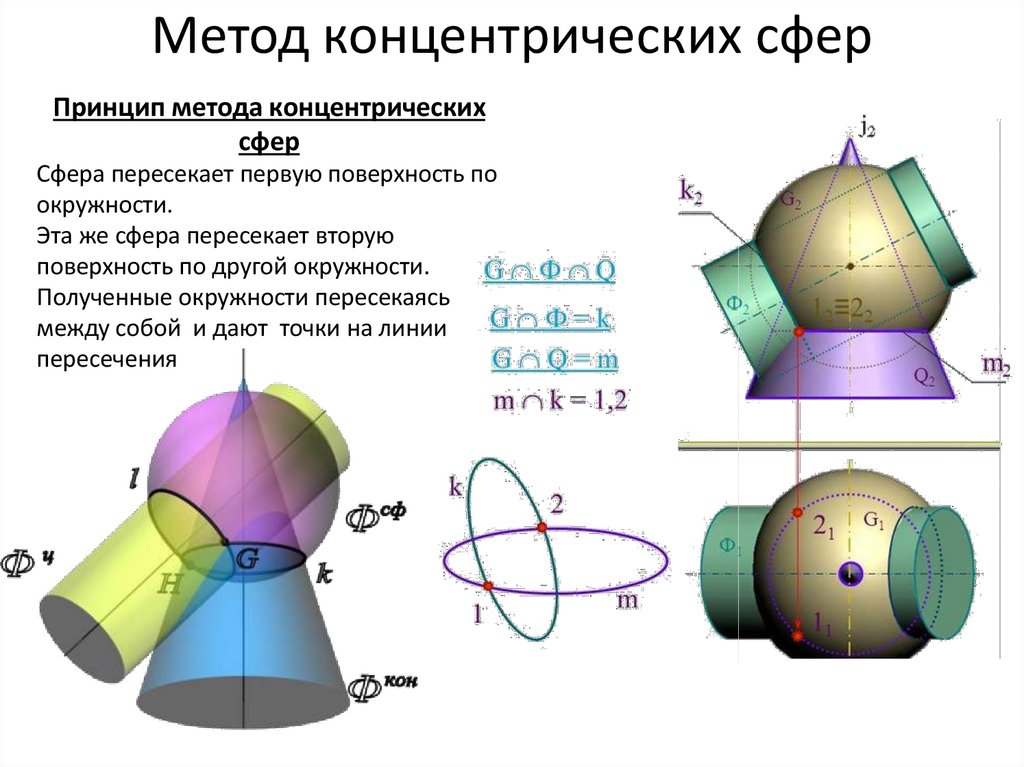
Принцип метода концентрических
сфер
Сфера пересекает первую поверхность по
окружности.
Эта же сфера пересекает вторую
поверхность по другой окружности.
Полученные окружности пересекаясь
между собой и дают точки на линии
пересечения

7.

8.

9.

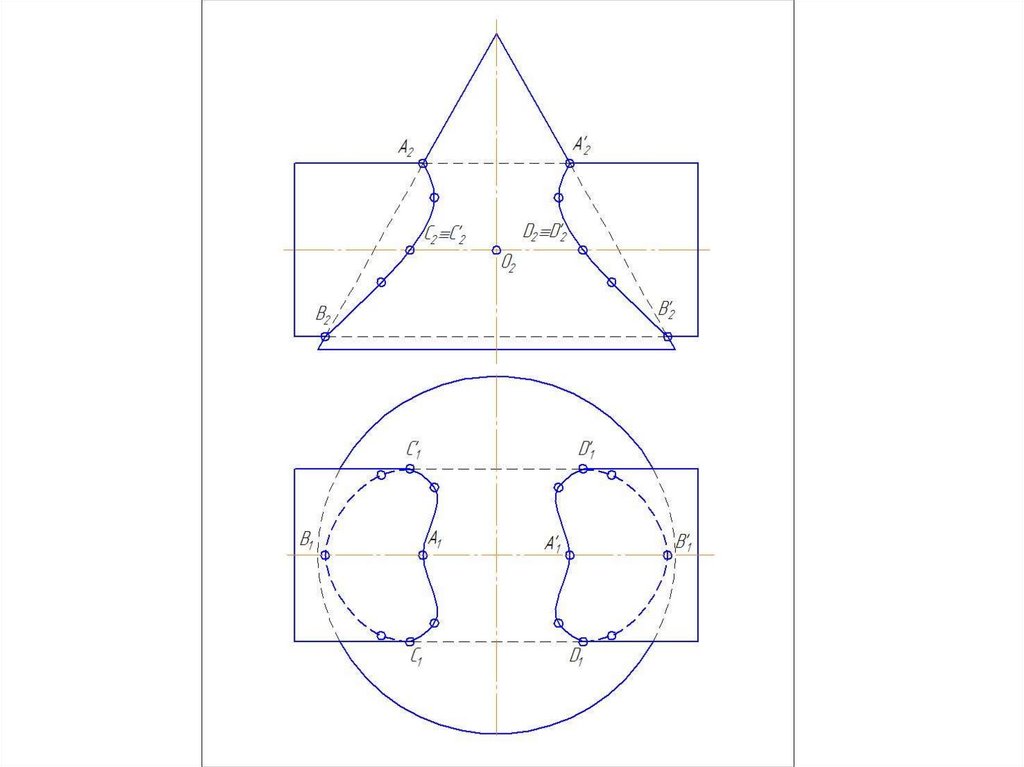
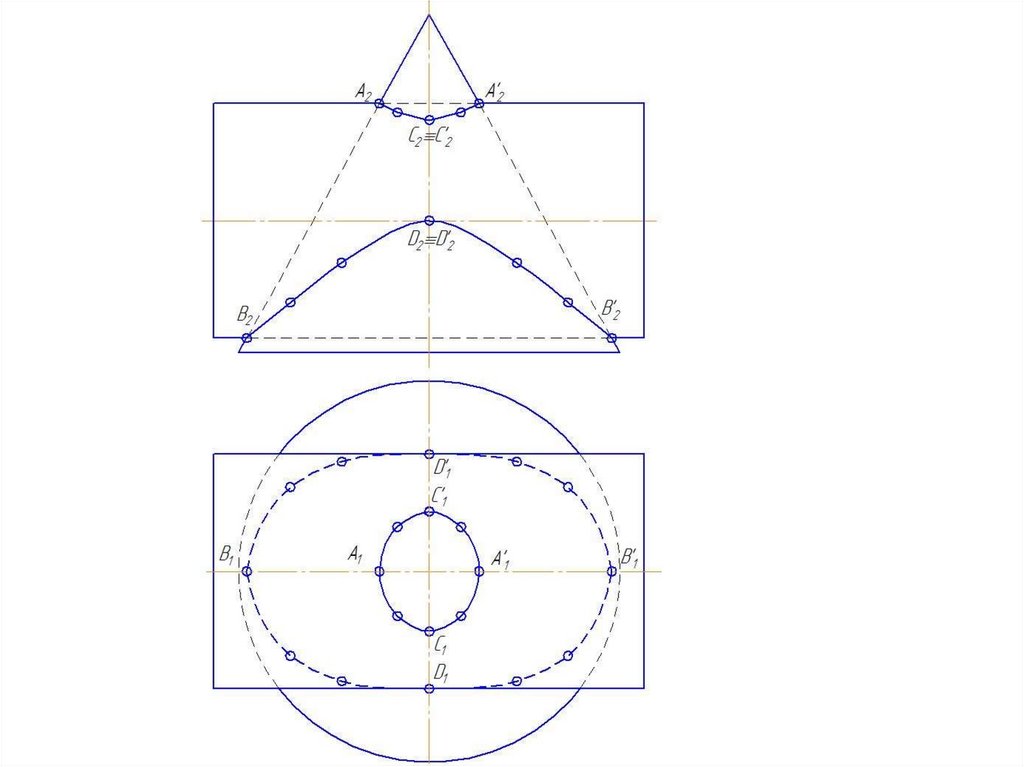
Алгоритм решения
Построения ведутся на той плоскости проекции,
которой параллельна плоскость общей симметрии
(на том где оси вращения проецируются как две
прямые линии)
1. Найти центр сфер (на пересечении осей
вращения)
2. Найти экстремальные точки (на пересечении
очерков)
3. Построить сферу максимального радиуса Rmax
(она проходит через наиболее удаленную от
центра сфер экстремальную точку)
4. Построить сферу минимального радиуса Rmin
Она lдолжна касаться одной поверхности и
пересекать вторую. Радиус вписанной сферы – это
перпендикуляр, опущенный из центра сфер на очерк
поверхности (из двух возможных радиусов выбирают
наибольший .
Сфера пересекает поверхность тора по кружности
проходящей через точку касания очерка сферы и
очерка тора (окружность лежит в плоскость
перпендикулярной оси вращения тора).
Эта же сфера пересекает конус по окружности,
проходящей через точки пересечения очерков
сферы и конуса (окружность лежит в плоскость
перпендикулярной оси вращения конуса).
Окружности пересекаясь дают искомые точки на
линии пересечения поверхностей

10.

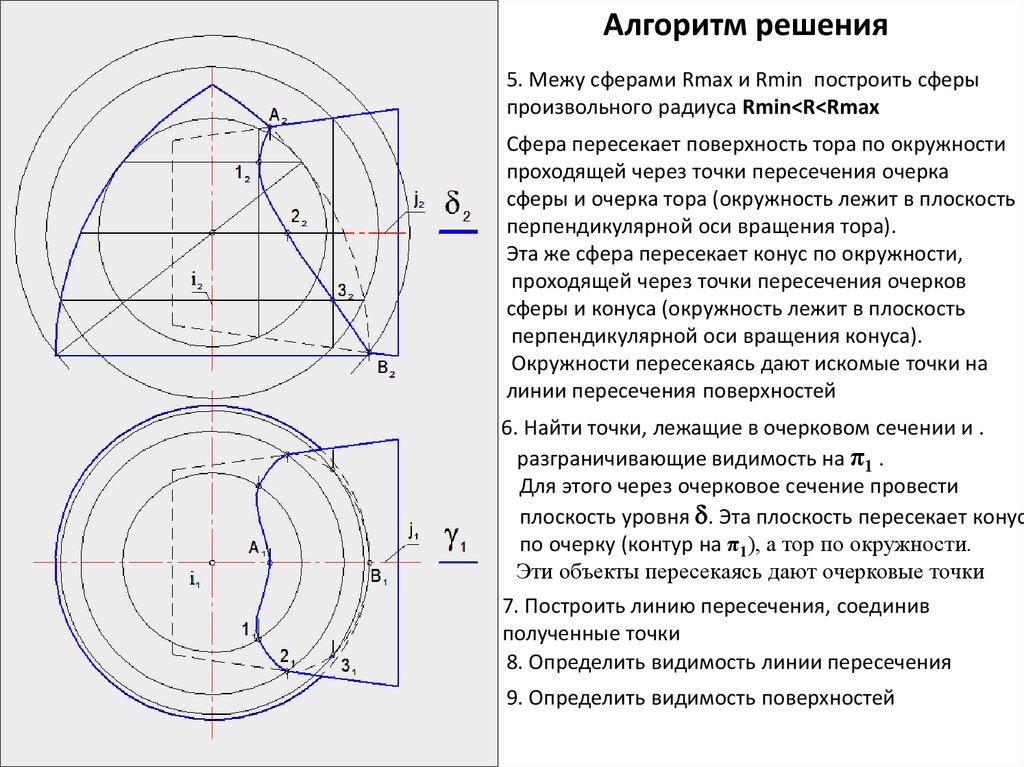
Алгоритм решения
5. Межу сферами Rmax и Rmin построить сферы
произвольного радиуса Rmin<R<Rmax
Сфера пересекает поверхность тора по окружности
проходящей через точки пересечения очерка
сферы и очерка тора (окружность лежит в плоскость
перпендикулярной оси вращения тора).
Эта же сфера пересекает конус по окружности,
проходящей через точки пересечения очерков
сферы и конуса (окружность лежит в плоскость
перпендикулярной оси вращения конуса).
Окружности пересекаясь дают искомые точки на
линии пересечения поверхностей
6. Найти точки, лежащие в очерковом сечении и .
разграничивающие видимость на π1 .
Для этого через очерковое сечение провести
плоскость уровня . Эта плоскость пересекает конус
по очерку (контур на π1), а тор по окружности.
Эти объекты пересекаясь дают очерковые точки
7. Построить линию пересечения, соединив
полученные точки
8. Определить видимость линии пересечения
9. Определить видимость поверхностей