Похожие презентации:
Взаимное пересечение поверхностей. Лекция 8
1.
Взаимное пересечениеповерхностей
2.
Для построения линиипересечения поверхностей
используют вспомогательные
плоскости (посредники). Их задают
так, чтобы они пересекали данные
поверхности по наиболее простым
линиям.
3.
Далее строят линии пересечениявспомогательных плоскостей с
каждой поверхностью и
отмечают точки пересечения
границ сечений.
Эти точки принадлежат
искомой линии сечения.
4.
Способ вспомогательныхсекущих плоскостей
5.
Пересечение поверхностей может быть полным – «проницание» (приэтом образуется две замкнутые линии пересечения); или не полным –
«врезка» (образуется одна замкнутая линия пересечения).
6.
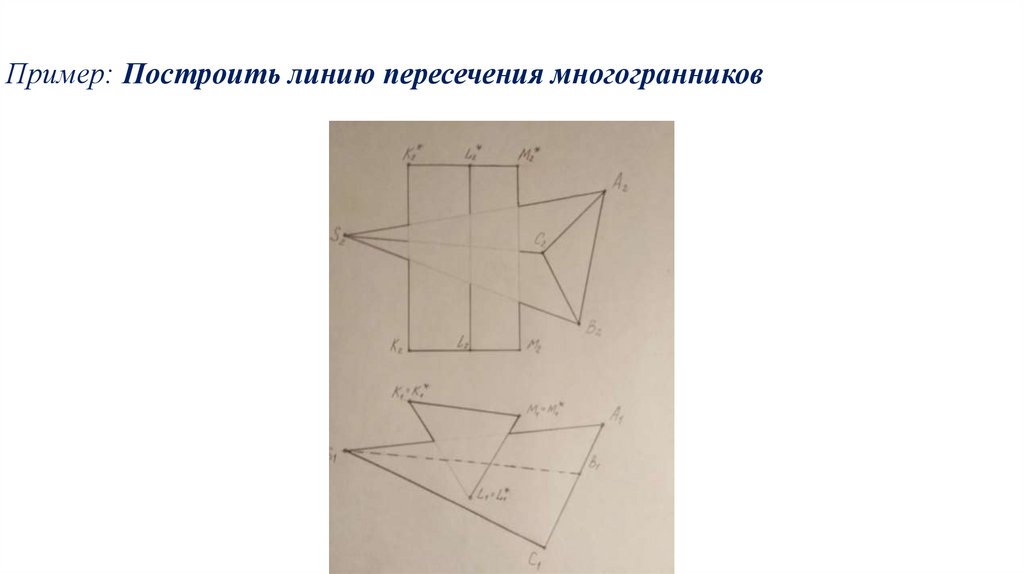
Пример: Построить линию пересечения многогранников7.
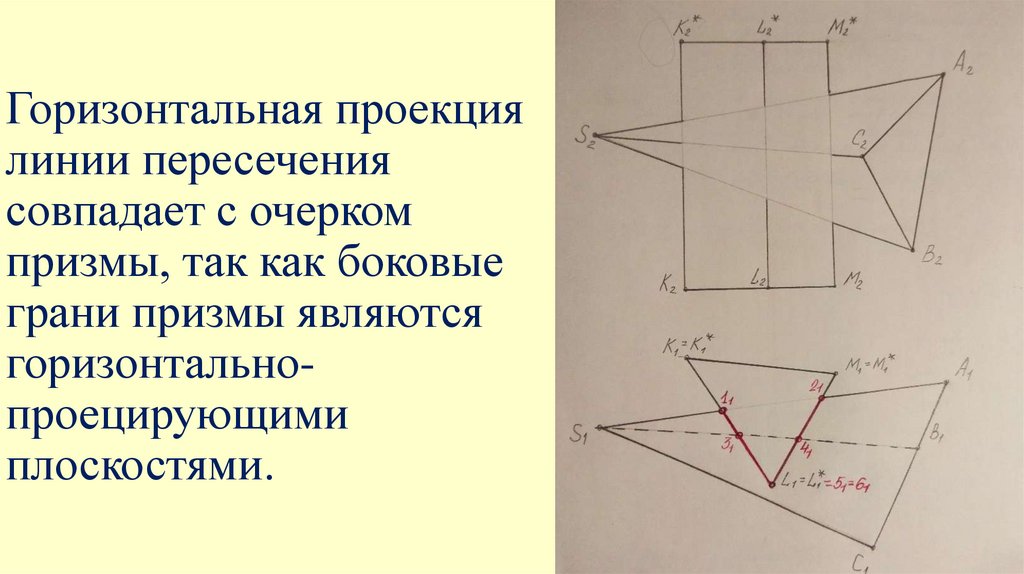
Горизонтальная проекциялинии пересечения
совпадает с очерком
призмы, так как боковые
грани призмы являются
горизонтальнопроецирующими
плоскостями.
8.
Точки 1, 2, 3, 4 являютсяточками пересечения ребер
пирамиды SA и SB с
гранями призмы.
9.
Точки 5 и 6 построены как точкипересечения ребра В призмы с
гранями пирамиды. Для этого
через вершину пирамиды S
задана вспомогательная
плоскость, которая пересекает
пирамиду по треугольнику SMN.
Точки 5 и 6 есть результат
пересечения линий SM и SN с
ребром В. Видимыми отрезками
линии пересечения будут те,
которые принадлежат видимым
граням.
10.
Пример. Построить линию пересечения конуса ицилиндра.
11.
Цилиндр занимает фронтальнопроецирующее положение,
поэтому линия пересечения на
фронтальной проекции
совпадает с контуром
цилиндра.
Построение начинают с
определения точек
пересечения очерковых линий
(точки 1 и 2).
12.
Задают вспомогательнуюплоскость, которая
пересекает конус по
окружности, а цилиндр по
прямым линиям. Точки
пересечения этих линий
лежат на линии пересечения
поверхностей.
Соединяем полученные
точки на горизонтальной
проекции.
13.
Некоторые особые случаи пересеченияповерхностей вращения
14.
Соосные поверхности вращенияпересекаются по окружностям,
которые лежат в плоскостях,
перпендикулярных оси вращения.
Соосными называют поверхности,
имеющие общую ось вращения.
15.
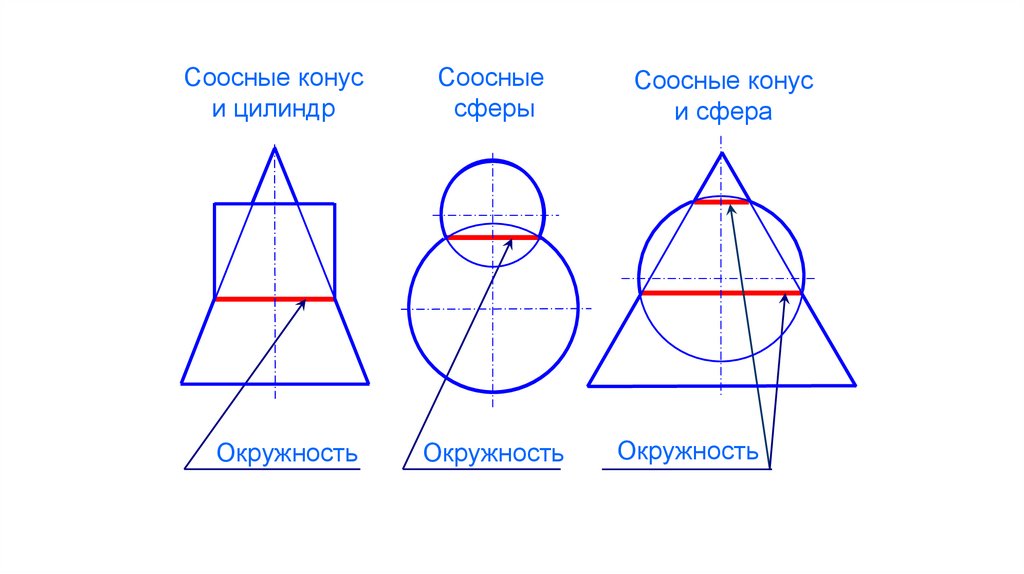
Соосные конуси цилиндр
Окружность
Соосные
сферы
Окружность
Соосные конус
и сфера
Окружность
16.
ТЕОРЕМА МОНЖАЕсли две поверхности вращения описаны
вокруг общей сферы, то линия пересечения
этих поверхностей распадается на две
плоские кривые второго порядка (эллипсы).
17.
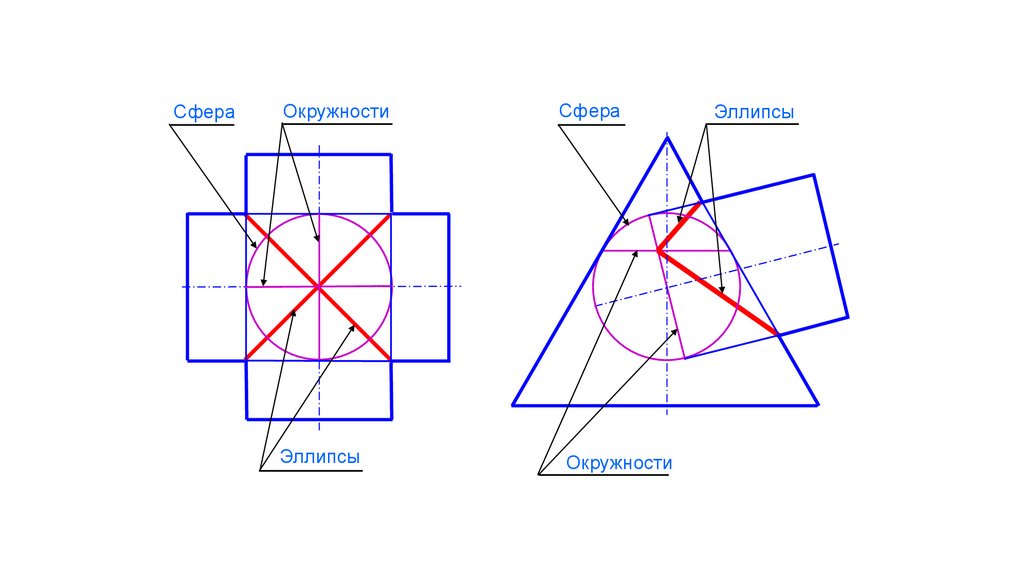
СфераОкружности
Эллипсы
Сфера
Окружности
Эллипсы
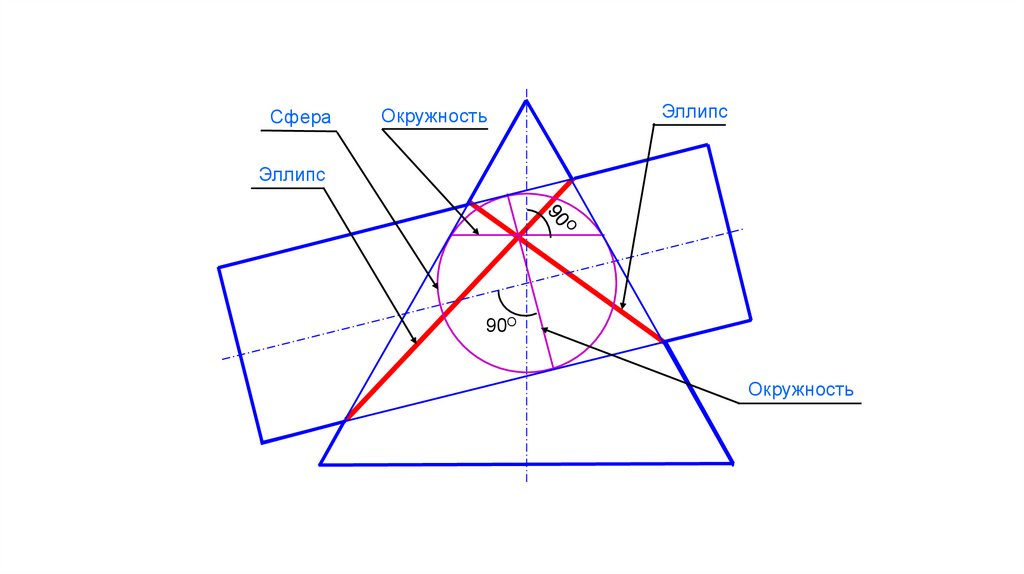
18.
СфераОкружность
Эллипс
Эллипс
90О
Окружность
19.
•Приведены примеры пересечения двухцилиндров
и цилиндра с конусом.
•Линией пересечения этих
поверхностей являются эллипсы.
20.
Способ вспомогательных концентрическихсфер
Способ концентрических сфер применяется если:
1. Обе данные поверхности - поверхности вращения.
2. Оси поверхностей должны пересекаться.
3. Оси их должны быть параллельны одной из
плоскостей проекций.
21.
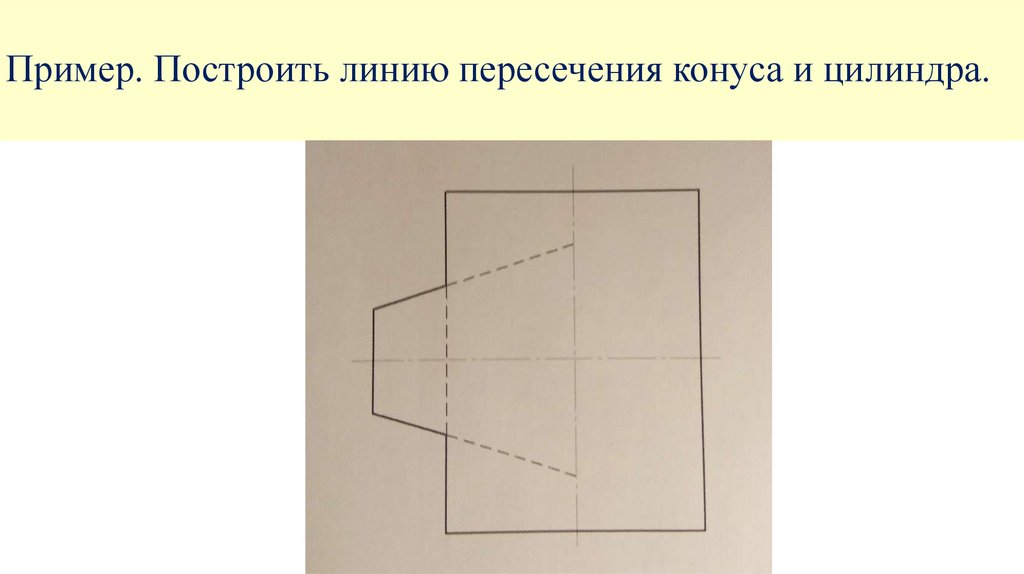
Пример. Построить линию пересечения конуса и цилиндра.22.
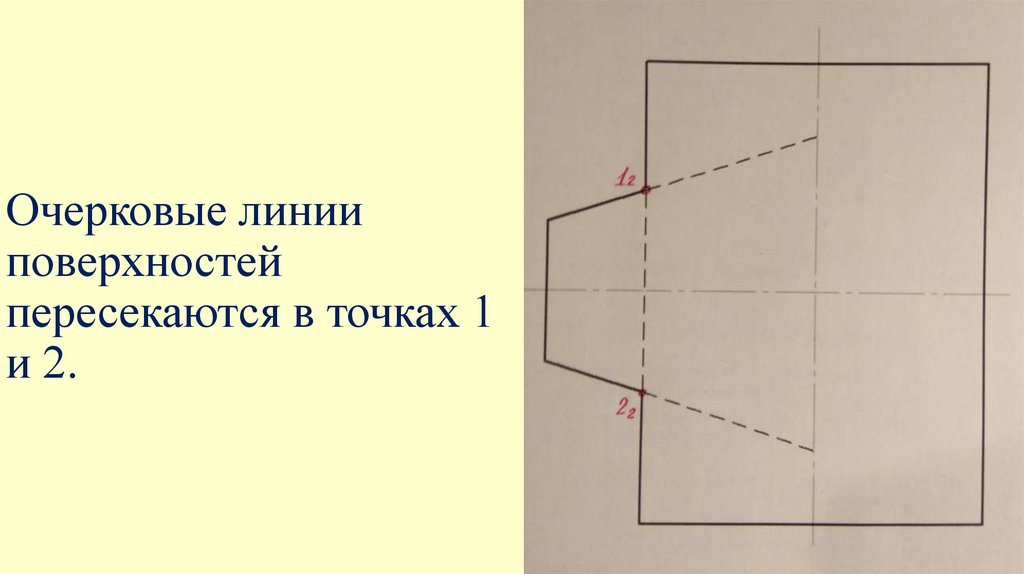
Очерковые линииповерхностей
пересекаются в точках 1
и 2.
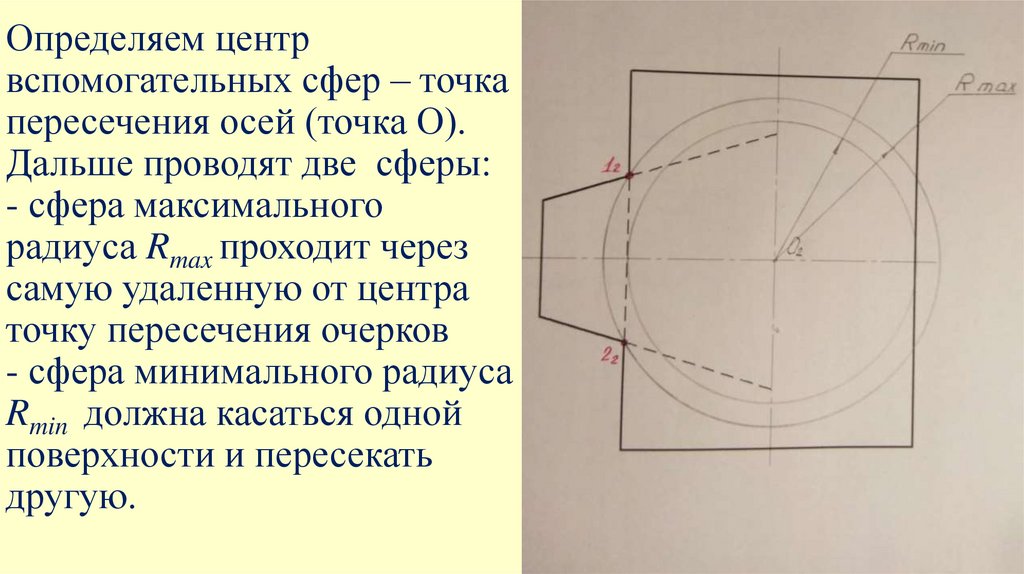
23.
Определяем центрвспомогательных сфер – точка
пересечения осей (точка О).
Дальше проводят две сферы:
- сфера максимального
радиуса Rmax проходит через
самую удаленную от центра
точку пересечения очерков
- сфера минимального радиуса
Rmin должна касаться одной
поверхности и пересекать
другую.
24.
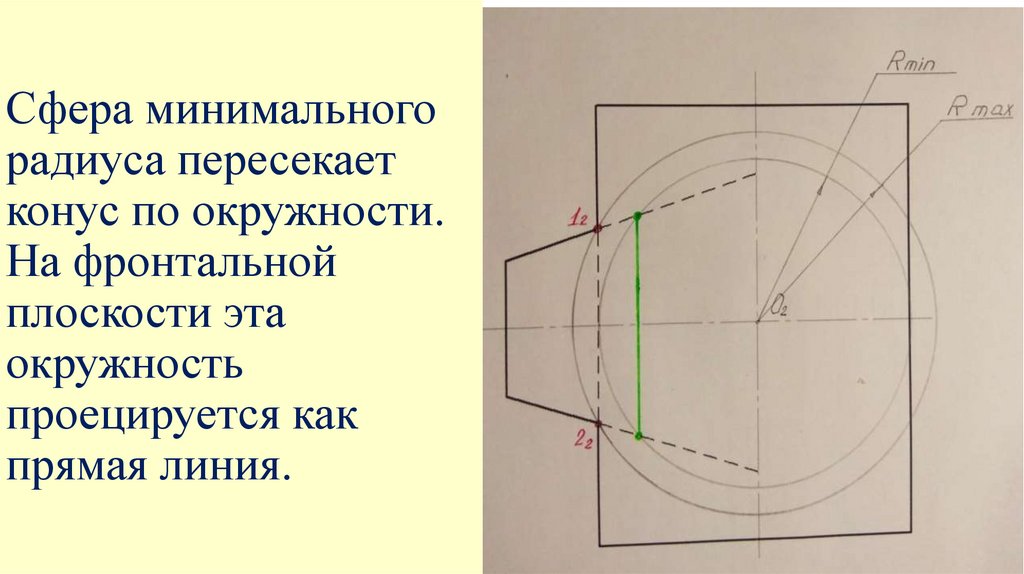
Сфера минимальногорадиуса пересекает
конус по окружности.
На фронтальной
плоскости эта
окружность
проецируется как
прямая линия.
25.
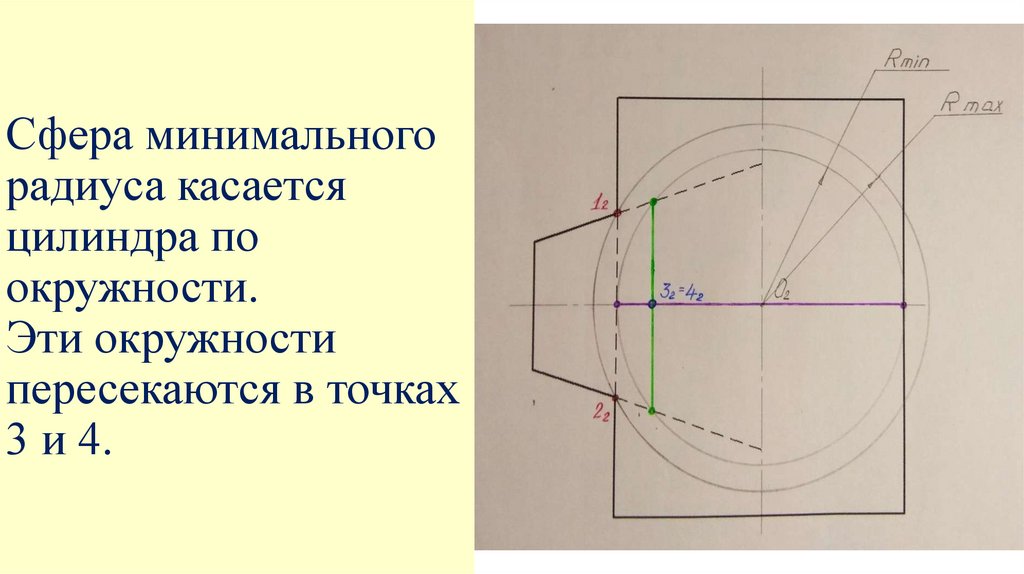
Сфера минимальногорадиуса касается
цилиндра по
окружности.
Эти окружности
пересекаются в точках
3 и 4.
26.
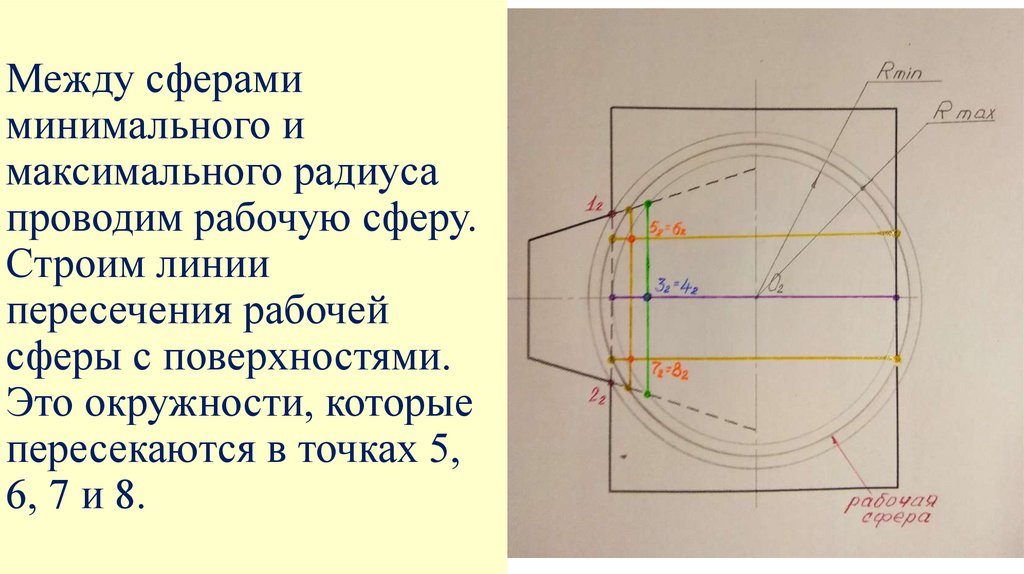
Между сферамиминимального и
максимального радиуса
проводим рабочую сферу.
Строим линии
пересечения рабочей
сферы с поверхностями.
Это окружности, которые
пересекаются в точках 5,
6, 7 и 8.
27.
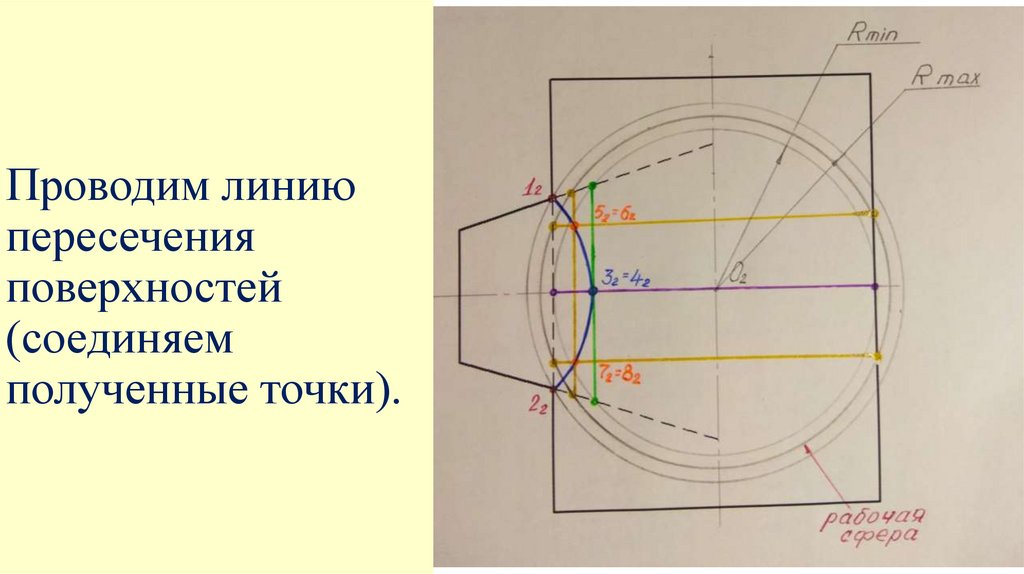
Проводим линиюпересечения
поверхностей
(соединяем
полученные точки).
















 Математика
Математика








