13. Взаимное пересечение 2021

1.

ГАПОУ СО «Уральский колледж строительства, архитектуры и
предпринимательства» (УКСАП)
Преподаватель
Н.С. Оконишникова

Тема «Взаимное пересечение поверхностей геометрических тел» является
завершающей в ряду позиционных задач (пересечение прямых, плоскостей,
поверхности с плоскостью), решение которых сводится к одним и тем же
действиям:
• найти общие точки исходных геометрических тел;
• соединив общие точки, построить линию взаимного пересечения;
• определить видимость.
Задачи на взаимное пересечение поверхностей бывают двух типов:
а - когда сохранены оба
пересекающихся тела
б - когда одно из
тел вырезано
Ход решения таких задач
различается только на этапе
определения видимости

3.

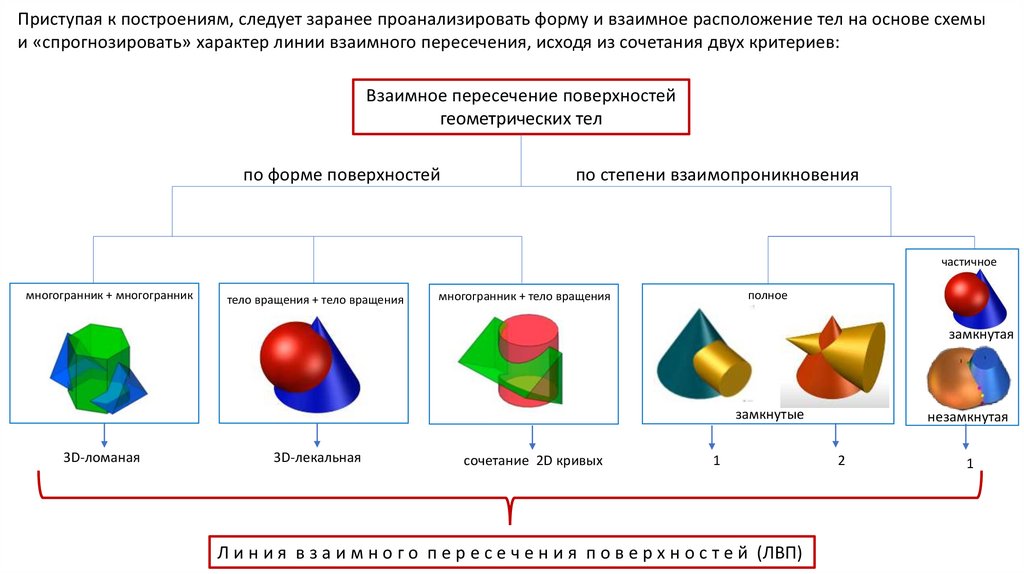
Приступая к построениям, следует заранее проанализировать форму и взаимное расположение тел на основе схемы
и «спрогнозировать» характер линии взаимного пересечения, исходя из сочетания двух критериев:
Взаимное пересечение поверхностей
геометрических тел
по форме поверхностей
по степени взаимопроникновения
частичное
многогранник + многогранник
тело вращения + тело вращения
полное
многогранник + тело вращения
замкнутая
замкнутые
3D-ломаная
3D-лекальная
cочетание 2D кривых
1
Л и н и я в з а и м н о г о п е р е с е ч е н и я п о в е р х н о с т е й (ЛВП)
незамкнутая
2
1

4.

Способы построения линии взаимного пересечения
1.
2.
Способ вспомогательных секущих плоскостей (универсальный)
Способ вспомогательных концентрических секущих сфер; он может применяться, если:
оба пересекающихся тела – тела вращения;
оси вращения тел – пересекающиеся прямые.
Способ (2) основан на свойстве сферы пересекаться с любой соосной
с ней поверхностью вращения по окружности.

5.

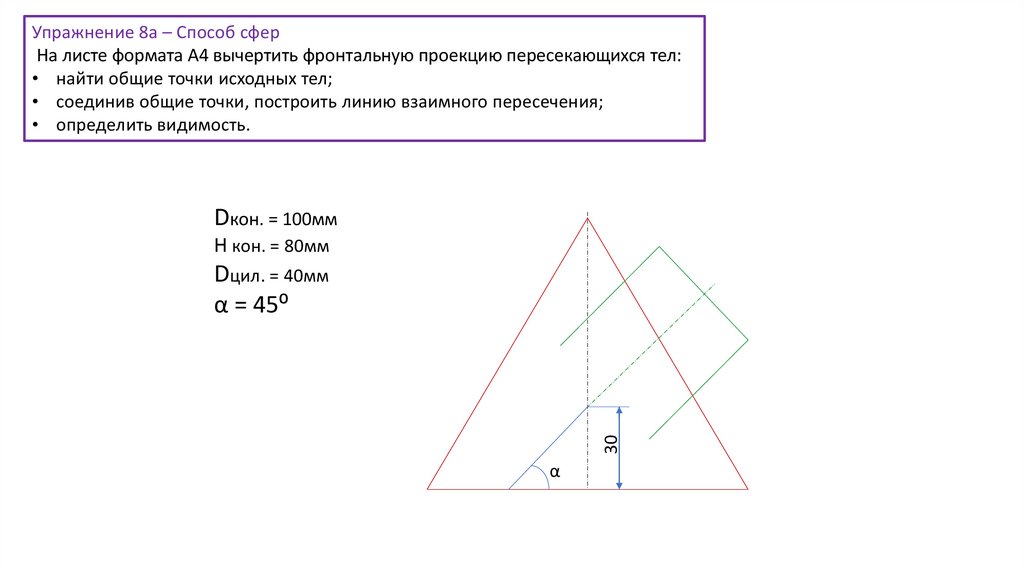
Упражнение 8а – Способ сфер
На листе формата А4 вычертить фронтальную проекцию пересекающихся тел:
• найти общие точки исходных тел;
• соединив общие точки, построить линию взаимного пересечения;
• определить видимость.
Dкон. = 100мм
Н кон. = 80мм
30
Dцил. = 40мм
α = 45⁰
α

6.

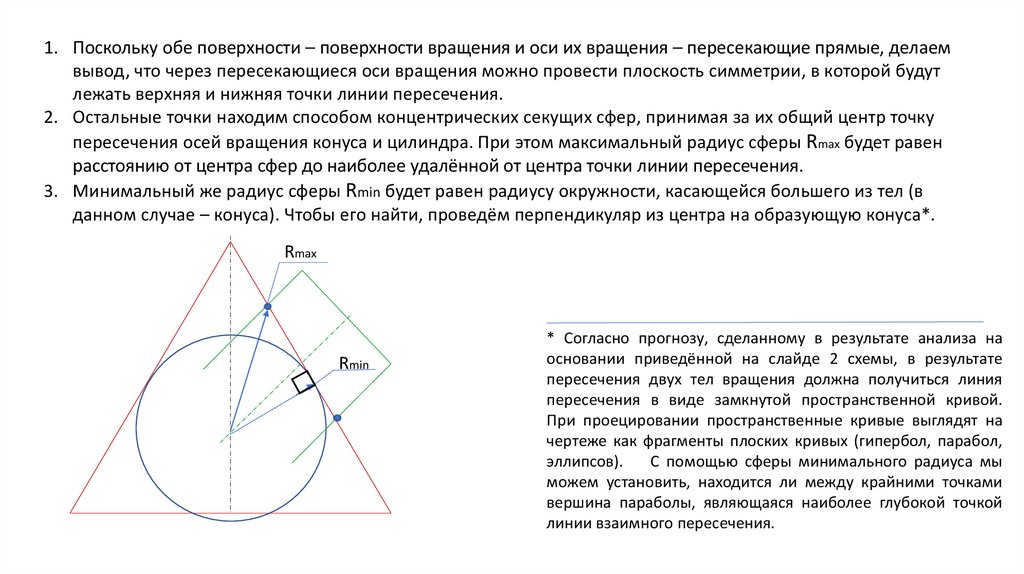
1. Поскольку обе поверхности – поверхности вращения и оси их вращения – пересекающие прямые, делаем
вывод, что через пересекающиеся оси вращения можно провести плоскость симметрии, в которой будут
лежать верхняя и нижняя точки линии пересечения.
2. Остальные точки находим способом концентрических секущих сфер, принимая за их общий центр точку
пересечения осей вращения конуса и цилиндра. При этом максимальный радиус сферы Rmax будет равен
расстоянию от центра сфер до наиболее удалённой от центра точки линии пересечения.
3. Минимальный же радиус сферы Rmin будет равен радиусу окружности, касающейся большего из тел (в
данном случае – конуса). Чтобы его найти, проведём перпендикуляр из центра на образующую конуса*.
Rmax
Rmin
* Согласно прогнозу, сделанному в результате анализа на
основании приведённой на слайде 2 схемы, в результате
пересечения двух тел вращения должна получиться линия
пересечения в виде замкнутой пространственной кривой.
При проецировании пространственные кривые выглядят на
чертеже как фрагменты плоских кривых (гипербол, парабол,
эллипсов).
С помощью сферы минимального радиуса мы
можем установить, находится ли между крайними точками
вершина параболы, являющаяся наиболее глубокой точкой
линии взаимного пересечения.

7.

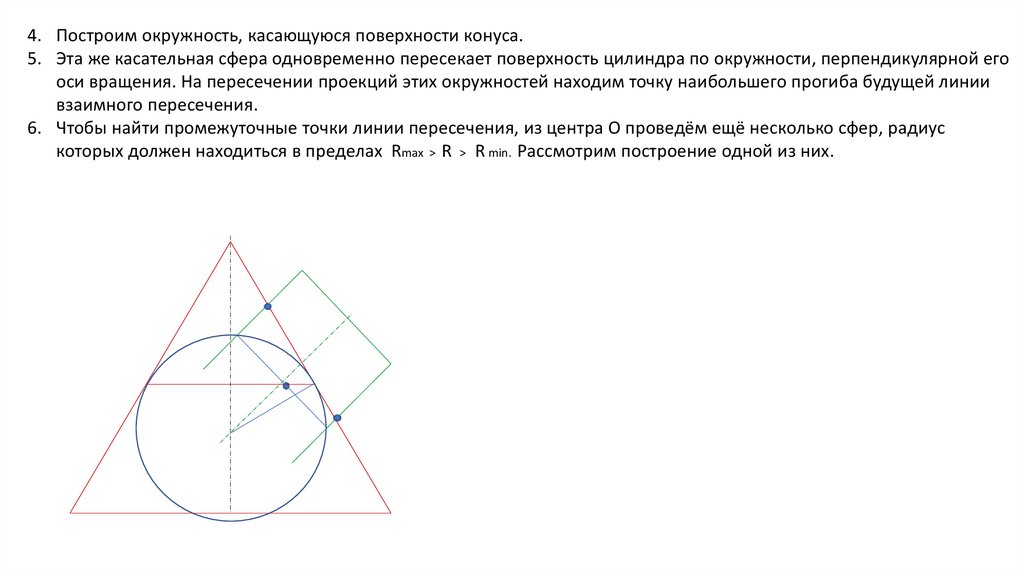
4. Построим окружность, касающуюся поверхности конуса.
5. Эта же касательная сфера одновременно пересекает поверхность цилиндра по окружности, перпендикулярной его
оси вращения. На пересечении проекций этих окружностей находим точку наибольшего прогиба будущей линии
взаимного пересечения.
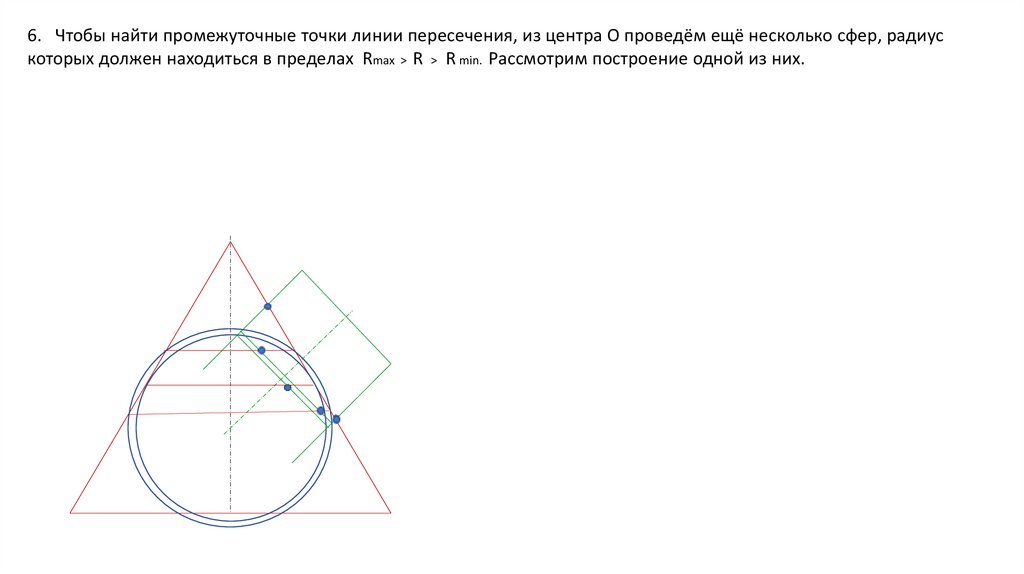
6. Чтобы найти промежуточные точки линии пересечения, из центра О проведём ещё несколько сфер, радиус
которых должен находиться в пределах Rmax > R > R min. Рассмотрим построение одной из них.

8.

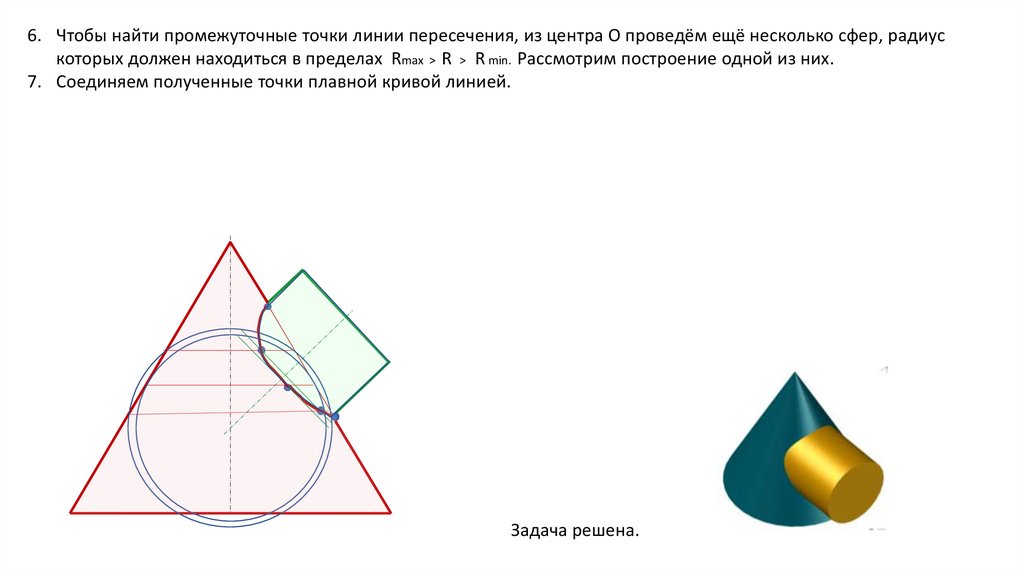
6. Чтобы найти промежуточные точки линии пересечения, из центра О проведём ещё несколько сфер, радиус
которых должен находиться в пределах Rmax > R > R min. Рассмотрим построение одной из них.

9.

10.

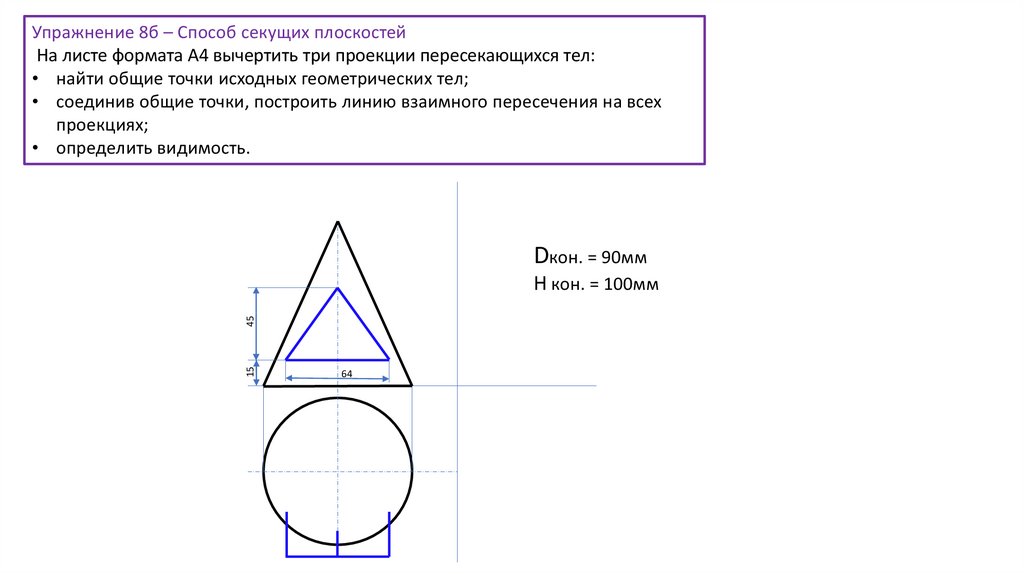
Упражнение 8б – Способ секущих плоскостей
На листе формата А4 вычертить три проекции пересекающихся тел:
• найти общие точки исходных геометрических тел;
• соединив общие точки, построить линию взаимного пересечения на всех
проекциях;
• определить видимость.
Dкон. = 90мм
15
45
Н кон. = 100мм
64

11.

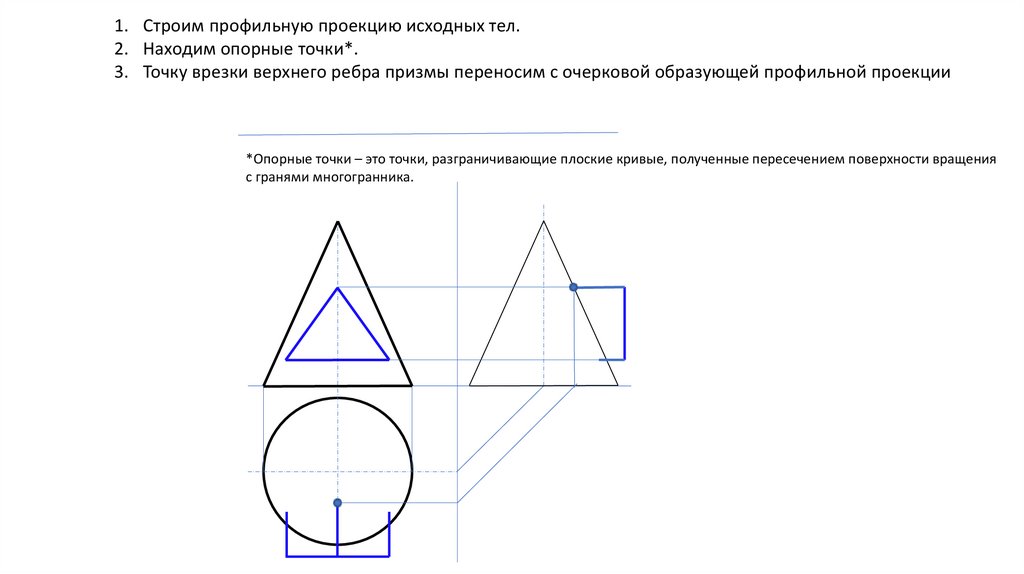
1. Строим профильную проекцию исходных тел.
2. Находим опорные точки*.
3. Точку врезки верхнего ребра призмы переносим с очерковой образующей профильной проекции
*Опорные точки – это точки, разграничивающие плоские кривые, полученные пересечением поверхности вращения
с гранями многогранника.

12.

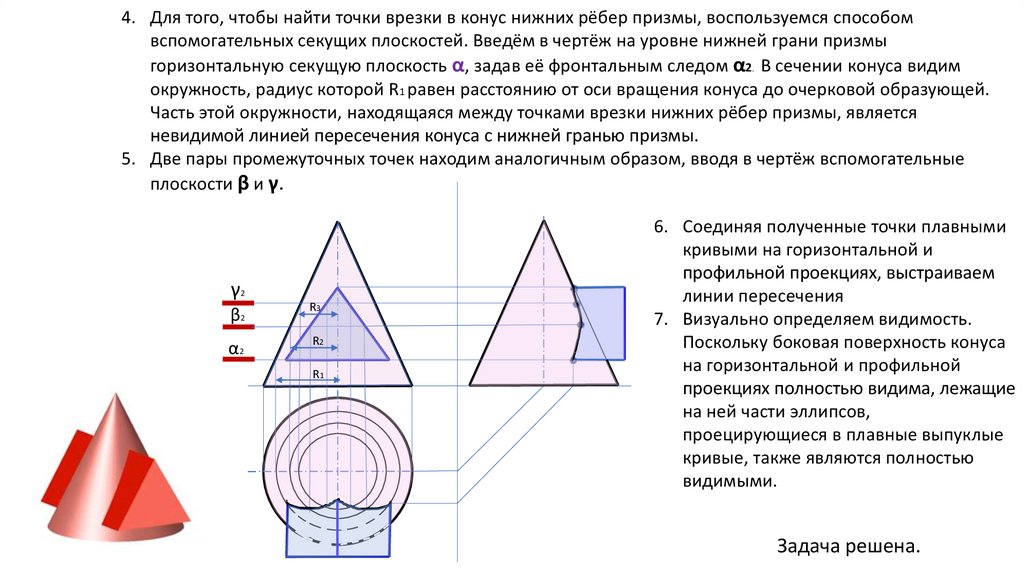
4. Для того, чтобы найти точки врезки в конус нижних рёбер призмы, воспользуемся способом
вспомогательных секущих плоскостей. Введём в чертёж на уровне нижней грани призмы
горизонтальную секущую плоскость α, задав её фронтальным следом α2. В сечении конуса видим
окружность, радиус которой R1 равен расстоянию от оси вращения конуса до очерковой образующей.
Часть этой окружности, находящаяся между точками врезки нижних рёбер призмы, является
невидимой линией пересечения конуса с нижней гранью призмы.
5. Две пары промежуточных точек находим аналогичным образом, вводя в чертёж вспомогательные
плоскости β и γ.
γ2
β2
R3
α2
R2
R1
6. Соединяя полученные точки плавными
кривыми на горизонтальной и
профильной проекциях, выстраиваем
линии пересечения
7. Визуально определяем видимость.
Поскольку боковая поверхность конуса
на горизонтальной и профильной
проекциях полностью видима, лежащие
на ней части эллипсов,
проецирующиеся в плавные выпуклые
кривые, также являются полностью
видимыми.
Задача решена.

13.

Методические указания к графическим работам
Работы 4а и 4б выполняются с использованием способа вспомогательных секущих плоскостей,
положение которых выбирается студентом самостоятельно, исходя из следующих принципов:
В сечении должны получаться достаточно простые геометрические фигуры (многоугольники,
окружности), которые, пересекаясь между собой, позволяют найти общие для обеих пересекающихся
поверхностей точки, принадлежащие линии взаимного пересечения.
Многогранники пересекаются по пространственной ломаной линии, вершины которой находятся там, где рѐбра
одного многогранника входят в рѐбра и грани другого.
При пересечении многогранника с телом вращения линия взаимного пересечения представляет собой сочетание
плоских кривых, переходящих одна в другую в характерных точках, где рѐбра многогранника входят в тело
вращения. Эти точки определяют в первую очередь, а затем переходят к нахождению промежуточных точек.
Соединяя все найденные точки между собой, получают линию взаимного пересечения, разграничивающую тела.
Особое внимание нужно уделить определению видимости на чертеже, когда линия пересечения уходит за очерки
тел.
При построении изометрической проекции точки, принадлежащие линии пересечения находят по координатам,
снятым с ортогонального чертежа. При этом нужно следить, чтобы точки не выходили за очерки тел (овалы,
лежащие в основании тел вращения, нужно чертить по изученному ранее «удлинѐнному» способу).

14.

Графическая работа 4а - Пересечение многогранников
(формат А3)
Содержание задания
1. Построить три проекции группы из двух пересекающихся многогранников, сохранив их взаимное
расположение*.
2.
Выполнить изометрическую проекцию.
3.
Построить на всех проекциях линию взаимного пересечения поверхностей тел. Определить видимость.
*Варианты задания размещены в
приложении 1
Пример выполнения работы

15.

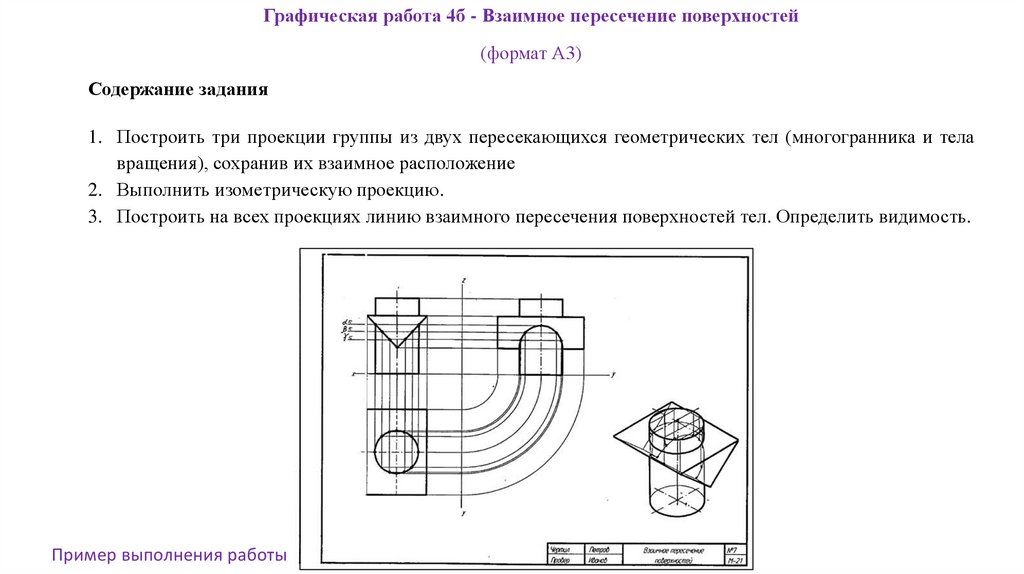
Графическая работа 4б - Взаимное пересечение поверхностей
(формат А3)
Содержание задания
1. Построить три проекции группы из двух пересекающихся геометрических тел (многогранника и тела
вращения), сохранив их взаимное расположение
2. Выполнить изометрическую проекцию.
3. Построить на всех проекциях линию взаимного пересечения поверхностей тел. Определить видимость.
Пример выполнения работы

16.

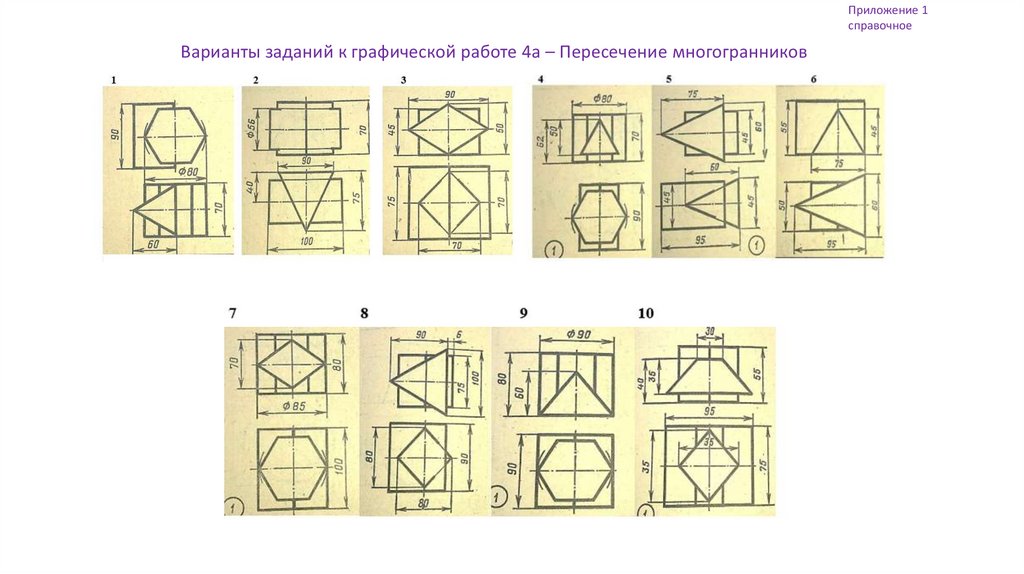
Приложение 1
справочное
Варианты заданий к графической работе 4а – Пересечение многогранников

17.

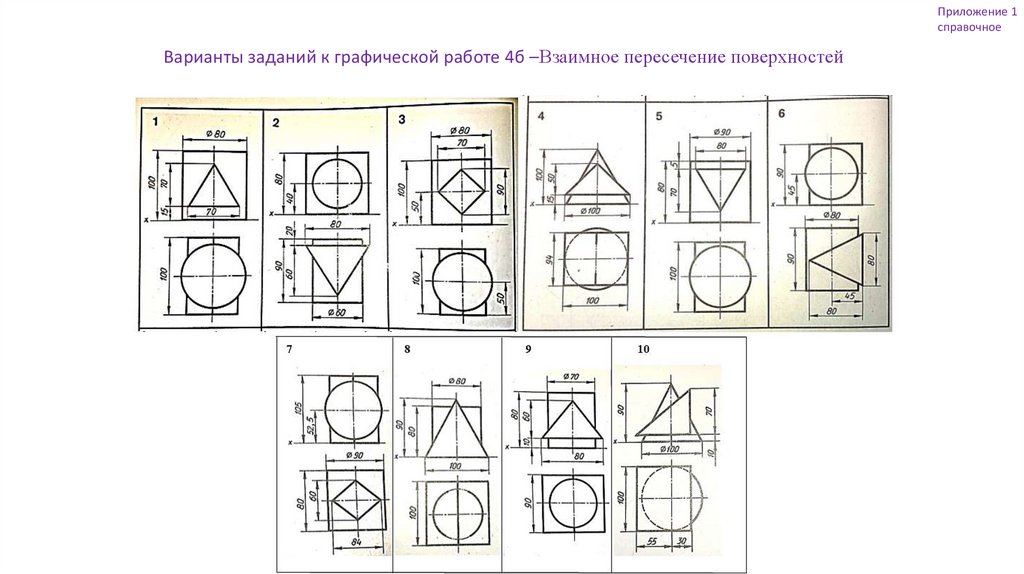
Приложение 1
справочное
Варианты заданий к графической работе 4б –Взаимное пересечение поверхностей

18.

Библиография
Основные источники:
1. Томилова, С.В. Инженерная графика. Строительство: Учебник для студ. СПО.
М.: Академия, 2012
Тема 1.6 – с.140-149;
Тема 1.7 – с.179-187.
Дополнительные источники:
1. Миронов, Б.Г., Миронова, Р.С. Сборник заданий по инженерной графике. – М.: Академия, 2012
Интернет – источники:
http://www.monographies.ru/67
http://grafika.stu.ru/wolchin/umm/in_graph/ig/003/000.htm
https://www.youtube.com/watch?v=9XIZ8HrXQJk

English Русский Правила