Лекция_1_Программа_и_Математические_методы

1. Лекция 1. Введение в динамику вязкой жидкости и газа

Доктор физико-математических наук,
профессор Владимир Иванович Шалаев
1

2. 1-й семестр: Динамика вязкой жидкости

3. Программа курса, 1-й семестр

1. Математический аппарат динамики сплошной среды.
Скалярные функции, векторы и тензоры второго ранга
для описания движения сплошной среды. Дифференциальная алгебра работы со скалярными, векторными и тензорными функциями. Асимптотический подход к решению систем дифференциальных уравнений с малым
параметром: метод сращиваемых асимптотических
разложений
2. Задачи динамики сплошной среды. Движение по
каналам и трубам, понятие вязкого сопротивления. Движение атмосферы, движение со свободными границами
в реках, морях и океанах, влияние на климат. Гидромеханика движения надводных и подводных судов в средах
со свободными границами; использование движения атмосферы как механизма движения. Аэромеханика
движения летательных аппаратов в атмосфере,
подъёмная сила, сила сопротивления, момент вращения.

4. Программа курса , 1-й семестр

3. Физические основы механики жидкости и газа: молекулярная
структура и способы ее описания. Молекулярная теория
структуры жидкостей и газов, движение молекул и их
взаимодействие. Кинетическая теория движения молекул
вязкого газа, функция распределения молекул по скоростям,
взаимодействие молекул при движении, кинетическое
уравнение. Средние параметры движения молекул: средняя
скорость среды, давление и температура среды, внутренние
напряжения.
4. Концепция сплошной среды. Основные законы сохранения и
уравнения механики сплошной среды. Гипотезы Навье-Стокса
для внутренних напряжений в сжимаемой сплошной среде.
Уравнения Навье-Стокса для движения вязкой сжимаемой
сплошной среды
и краевые условия. Безразмерные
переменные в задачах механики сжимаемой сплошной среды.
Законы и параметры подобия для течений. 1’) В 1 см3 при
атмосферном давлении находится 1019 молекул, а на высоте 300 км— 109 молекул. В
самых совершенных вакуумных установках в 1 см3 находится 107 —108 молекул.

5.

Программа курса , 1-й семестр
7. Уравнения Стокса для несжимаемой среды в векторной
форме. Свойства и параметры подобия.
8. Уравнения Стокса в декартовых координатах,
Аналитические решения: скользящее течение КуэттаПуазейля, течение жидкости по наклонной пластине,
задача Пуазейля для прямоугольного канала, течение в
слое жидкости в открытом наклоненном прямоугольном
лотке, течение в эллиптической трубе, течение слоя
жидкости в эллиптическом лотке.
9. Уравнения Стокса в цилиндрических координатах.
Аналитические решения: течение Куэтта-Пуазейля,
течение Тэйлора-Куэтта между двумя вращающимися
цилиндрами, диффузия вихря (вихрь Озина), вихрь
Бюргерса,

6.

Программа курса , 1-й семестр
10. Особенности течений вязкой жидкости при больших
числах Рейнольдса. Понятие пограничного слоя. Вывод
уравнений двухмерного пограничного слоя, преобразование Блазиуса и функция тока.
11. Свойства уравнений двухмерного пограничного слоя,
функция тока. Автомодельные решения и условия их
существования, пограничные слои с нулевым градиентом
давления: течение около пластины, пограничный слой
Блазиуса; плоская струя в однородном газе, пристеночная струя, слой смешения, дальний след за телом.
12. Интегральные уравнения сохранения. Метод КарманаПольгаузена решения интегральных уравнений.
13.Осесимметричные пограничные слои. Преобразование Степанова-Манглера. Пограничный слой на цилиндре, круглая струя, след за цилиндром. Интегральный
метод для осесимметричного пограничного слоя.

7.

14. Второе приближение в теории пограничного слоя,
вязко-невязкое взаимодействие. Задачи взаимодействующих течений: ближний след (задача Месситера), отрыв
с гладкой поверхности.
15. Неустойчивость ламинарных течений вязкой
жидкости
и
ламинарно-турбулентный
переход.
Различные типы неустойчивостей в двухмерных и
трехмерных течениях. Физические механизмы ламинарнотурбулентного перехода.
16. Турбулентные течения вязкой жидкости . Уравнения
Рейнольдса для вязкого совершенного газа. Методы
замыкания уравнений Рейнольдса: модели турбулентной
вязкости различного уровня, моделирование напряжений
Рейнольдса.
7

8. Программа курса , 1-й семестр

17.
Современные
методы
моделирования
турбулентных течений: метод прямого численного
моделирования, метод крупных вихрей. Примеры.
21. Трехмерные пограничные слои. Численные методы
решения уравнений трехмерного пограничного слоя.
Асимптотический
подход
к
решению
уравнений
трехмерного пограничного слоя на крыльях и фюзеляжах
летательных аппаратов.

9. Литература

1.Лойцянский Л.Г. Механика жидкости и газа. М.: Дрофа,
2003, 840 с.
2.Лойцянский Л.Г. Ламинарный пограничный слой. М.:
Физматлит, 1962, 480 с.
3. Шлихтинг Г. Теория пограничного слоя.
4.H. Schlichting, R. Gersten. Boundary layer theory. Springer,
2000, 801 p.
5. В.И. Шалаев. Применение аналитических методов в
современной аэромеханике. Часть 1. Теория пограничного
слоя. М.: МФТИ, 2011, 360 с.

10. Создатели механики сплошной среды

10

11.

Исаа́к Нью́то́н; (25.12.1642-20.03.1727)
Предложил формулу для закона сопротивления тела в
разреженной среде (метод Ньютона) и на её основе
рассмотрел одну из первых задач об оптимальной форме
обтекаемого тела. Этот подход используется до сих пор
для оценки сопротивления гиперзвуковых аппаратов и
проектирования тел наименьшего сопротивления. Исаа́к
Нью́то́н также ввел понятие вязкости жидкости.

12.

Жозе́ф Луи́
Лагра́нж ( 25.01.1736
, Турин -10.04.1813,
Париж) Французский
математик, астроном
и механик итальянского происхождения.
Наряду с Эйлером — крупнейший математик XVIII века.
Автор классического трактата «Аналитическая механика»,
в котором установил фундаментальный «принцип возможных перемещений» и завершил математизацию механики.
Его работы – основа современной математики и механики.
В механике жидкости и газа метод Лагранжа – один из
основных подходов расчета течений.

13.

Дании́л
Берну́лли
(
(8.02.1700
—
17.031782)
швейцарский, физик, механик и математик, один из
создателей кинетической теории газов, гидродинамики
и математической физики. Главный труд монография
«Гидродинамика» (опубликована в 1738 году, закон
Бернулли). Формула Бернулли для давления – одна из
наиболее используемых в современной аэромеханике

14.

Леона́рд Эйлер 15.04.1707
Базель , Швейцария —
7 (18) .09 1783, СанктПетербург, Россия)
Швейцарский, прусский и российский математик и механик,
внёсший фундаментальный
вклад в развитие этих наук. Наряду с Лагранжем — крупнейший математик XVIII века, считается одним из величайших
математиков в истории. Эйлер — автор более чем 850
работ[по математическому анализу, дифференциальной
геометрии, теории чисел, приближённым
вычислениям небесной механике ,математической физике,
оптике, баллистике корабле-строению, теории музыки и др. .
Изучал медицину, химию, ботанику, воздухоплавание,
теорию музыки, множество языков. Уравнения Эйлера,
подход Эйлера в описании невязкой газовой динамики
одни из основных в современном мире

15.

Сэр Джордж Габрие́ль Стокс
13.08.1819-01.02.1903) английский математик, механик и
физик-теоретик ирландского
происхождения.
Работал
в
Кембриджском
университете,
внёс
значительный вклад в гидро- и газодинамику (уравнения
Навье
—
Стокса),
математическую
физику.
Член Лондонского королевского общества (1851), его
секретарь в 1854—1885 гг. и президент в 1885—1890 гг.
Уравнения Навье - Стокса, Стоксовы отношения, линия
Стокса, теорема Стокса, Стоксов сдвиг, закон Стокса –
это все широко используется в современном мире

16.

Лю́двиг
Бо́льцман
(20.02.1844,Вена,
5.09.1906
Дуино, Австро-Венгрия) — австрийский физик-теоретик,
основатель статистической механики и молекулярнокинетической теории. Его результаты – основа
современной статистической физики и теории газов

17.

О́сборн Рейнольдс
(23.08.1842, Белфаст — 21
02.1912 , Уотчет) –
английский механик, физик и
инженер, специалист в области
гидромеханики и гидравлики.
Член Лондонского королевского общества (1877).
Основоположник теории турбулентности в гидродинамике
Уравнения Рейнольдса – предмет ежедневного
обсуждения в аэромеханике.

18.

Людвиг Прандтль ( 4 февраля 1875
года, Фрайзинг — 15 августа 1953
года, Гёттинген).
Немецкий механик и физик. Внёс существенный вклад в
основы
гидродинамики
и
разработал
теорию
пограничного слоя. В честь его назван один из критериев
подобия, а также гидроаэрометрическое устройство,
ставшее
классическим
приёмником
воздушного
давления для самолётов и вертолётов.

19.

Никола́й Его́рович Жуко́вский (5 [17] января 1847,
Орехово Владимирская губерния — 17 марта 1921
г. Москва — русский учёный-механик, основоположник
гидро- и аэродинамики в России, создатель теории
подъемной силы. Стоял в основании ЦАГИ

20.

Серге́й Алексе́евич Чаплыгин
(24 марта [5 апреля] 1869, Раненбург, Р
язанская губерния — 8 октября 1942,
Новосибирск) – механик и математик,
один из основоположников
современной аэромеханики и аэродинамики, академик АН СССР(1929),
Герой Социалистического Труда (1941),
заслуженный деятель науки РСФСР
(1929). В конце 1918 года
привлечён Жуковским к организации ЦАГИ, где после Жуковского занял
руководящее положение (1921-1930 гг.
—председатель коллегии, 1928-1931
годах — директор-начальник).
В научно-теоретическом семинаре ЦАГИ под руководством
С. А. Чаплыгина вырос цвет отечественной механической науки
(М. А. Лаврентьев, М. В. Келдыш, Н. Е. Кочин, Л. И. Седов, Г. И. Петров,
Л. С. Лейбензон, С. А. Христианович и др.). В1931—1941 гг Чаплыгин
руководил созданием крупнейших аэродинамических
лабораторий ЦАГИ (

21.

Владимир Васильевич
Струми́нский (1914 — 1998) —учёный в
области аэродинамики, летательных
аппаратов и теоретических основ
самолётостроения. Академик АН СССР.
Лауреат Ленинской премии и двух Сталинских
премий. Разработал теорию трёхмерного
пограничного слоя и вихревую теорию крыла, общие принципы аэродинамической компоновки стреловидных и треугольных крыльев. Один из создателей транс- и сверхзвуковой реактивной авиации. Имеет фундаментальные работы по нелинейной теории устойчивости, динамической теории турбулентности, кинетической теории газов, по ламинаризации обтекания самолётов . Дтн (1947), член-корреспондент (1958), академик АН СССР (1966), первый заместитель начальника ЦАГИ (1953-1963), директор ИТПМ СОАН
(1966-1971)

22. Математический аппарат динамики сплошной среды

Системы координат. Скалярные, функции,
векторы и тензоры второго порядка для
описания движения сплошной среды.
Дифференциальные операторы работы со
скалярными, векторными и тензорными
функциями. Асимптотический подход к
решению систем дифференциальных
уравнений с малым параметром:
сращиваемые асимптотические
разложения
22

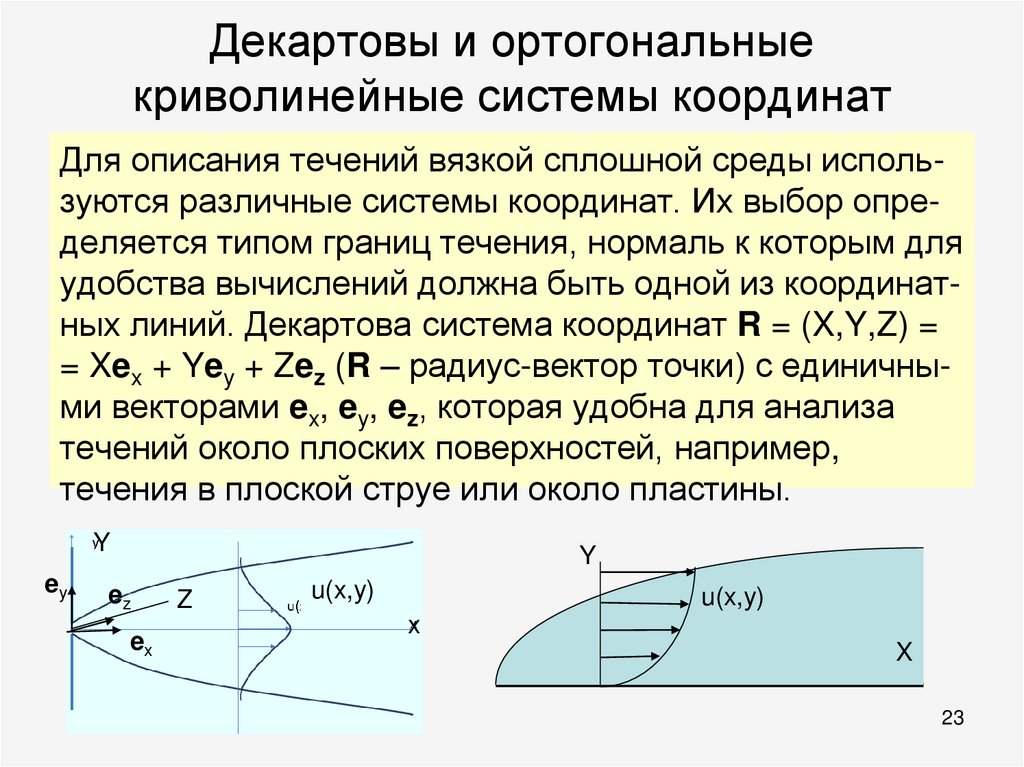
23. Декартовы и ортогональные криволинейные системы координат

Для описания течений вязкой сплошной среды используются различные системы координат. Их выбор определяется типом границ течения, нормаль к которым для
удобства вычислений должна быть одной из координатных линий. Декартова система координат R = (X,Y,Z) =
= Xex + Yey + Zez (R – радиус-вектор точки) с единичными векторами ex, ey, ez, которая удобна для анализа
течений около плоских поверхностей, например,
течения в плоской струе или около пластины.
Y
ey
Y
ez
ex
Z
u(x,у)
u(x,у)
x
X
23

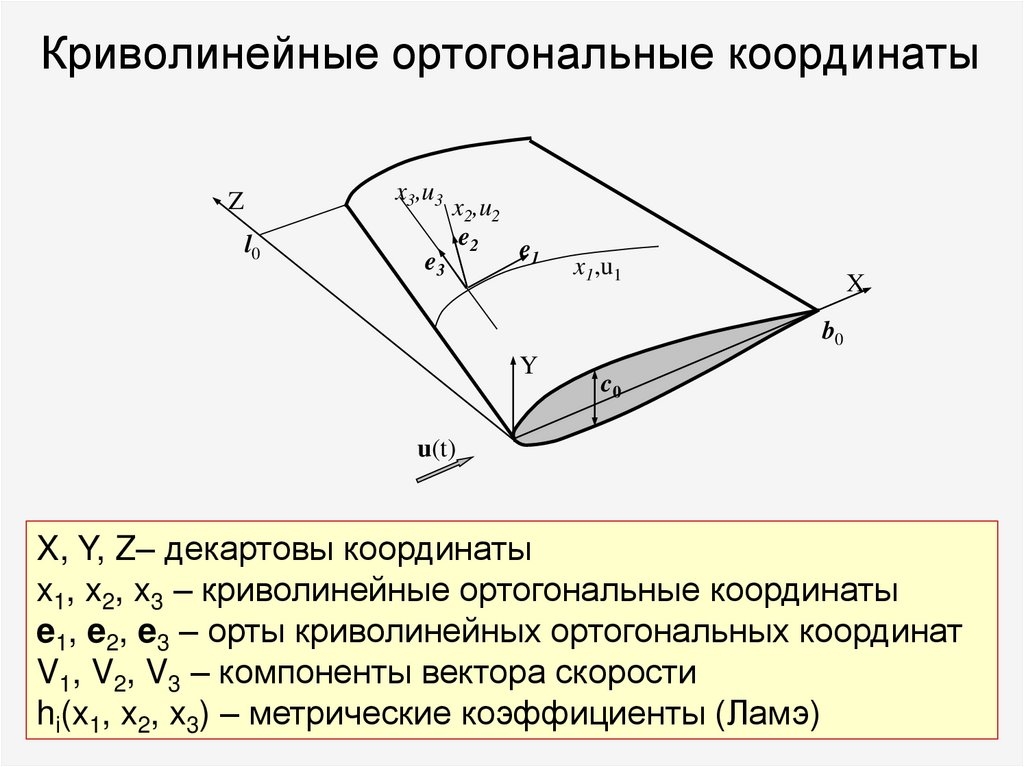
24. Криволинейные ортогональные координаты

Обычно используются при анализе обтекания тел с криволинейной поверхностью, например, крыла самолета.
x3,u3
Z
e3
x2,u2
e2 e1
x1,u1
X
b0
Y
e2 – единичный вектор
нормали к поверхности
e1 и e3 – параллельны
поверхности
c0
u(t)
X, Y, Z– декартовы координаты; x1, x2, x3 – криволинейные
ортогональные координаты; e1, e2, e3 – единичные векторы
(орты) криволинейных ортогональных координат;
u1(x1, x2, x3), u2(x1, x2, x3), u3(x1, x2, x3) – компоненты вектора
скорости; h1(x1, x2, x3), h2(x1, x2, x3), h3(x1, x2, x3) –
метрические коэффициенты (коэффициенты Ламэ)

25. Криволинейные ортогональные координаты

Радиус-вектор R x1 , x2 , x3
Z
l0
x3,u3
e3
x2,u2
e2 e1
Y
определяется уравнениями:
x1,u1
X
R x1 , x2 , x3 X , Y , Z
b0
Или: X R1 x1 , x2 , x3 ,
Y R2 x1 , x2 , x3 ,
c0
Z R3 x1 , x2 , x3
u(t)
Длина дифференциала радиус-вектора R :
dR e1h1dx1 e 2 h2 dx2 e3 h3 dx3 e1ds1 e2 ds2 e3 ds3
dR 2 h12 dx12 h22 dx22 h32 dx32 ; ei , i = 1,2,3 - единичные вектора (орты)
2
2
2
X Y Z
h
, i 1, 2,3 - коэффициенты Ламэ
xi xi xi
dsi hi dxi длины дуг дифференциалов координатных линий xi
2
i

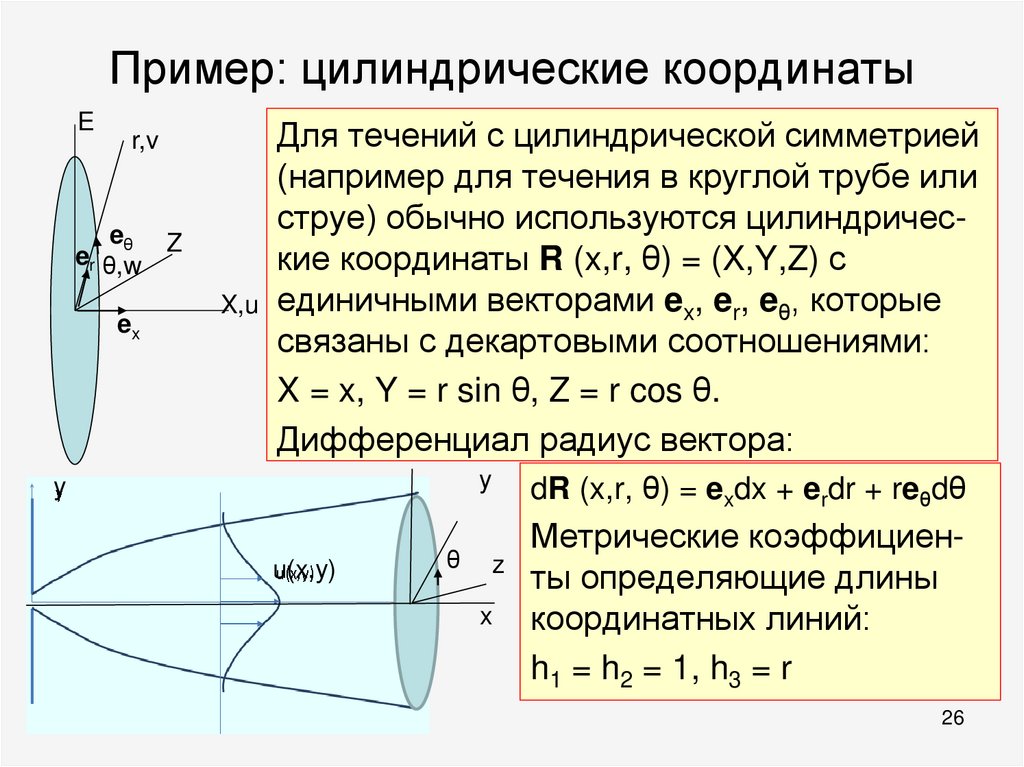
26. Пример: цилиндрические координаты

E
r,v
eθ
er θ,w Z
ex
Для течений с цилиндрической симметрией
(например для течения в круглой трубе или
струе) обычно используются цилиндрические координаты R (x,r, θ) = (X,Y,Z) с
X,u единичными векторами ex, er, eθ, которые
связаны с декартовыми соотношениями:
X = x, Y = r sin θ, Z = r cos θ.
Дифференциал радиус вектора:
y
y
u(x,у)
θ
dR (x,r, θ) = exdx + erdr + reθdθ
z
x
Метрические коэффициенты определяющие длины
координатных линий:
h1 = h2 = 1, h3 = r
26

27. Скалярные функции, характеризующие течения вязкой сжимаемой среды

Термодинамические переменные:
• Давление p(t,x1,x2,x3),
• Плотность ρ(t,x1,x2,x3)
• Температура Т(t,x1,x2,x3)
• Энтальпия h(t,x1,x2,x3) = cpT,
cp – теплоемкость при постоянном давлении.
В совершенном газе эти функции связаны уравнением
состояния
1
p RT
h
γ = cp/ cv, cv – теплоемкость при постоянном объеме газа.
μ (t,x1,x2,x3) и λ (t,x1,x2,x3) – коэффициенты вязкости и
27
теплопроводности

28. Векторы , характеризующие течения вязкой сжимаемой среды

Радиус-вектор
R x1 , x2 , x3 X , Y , Z
V(t,x1,x2,x3) – вектор скорости; F(t,x1,x2,x3) – вектор
внешних сил, например, вектор силы тяжести;
D(t,x1,x2,x3) – вектор силы сопротивления
движения тела в сплошной среде и др.
V V1 ,V2 ,V3 e1V1 e2V2 e3V3 eiVi
F F1 , F2 , F3 e1 F1 e2 F2 e3 F3 ei Fi
D D1 , D2 , D3 e1 D1 e2 D2 e3 D3 ei Di

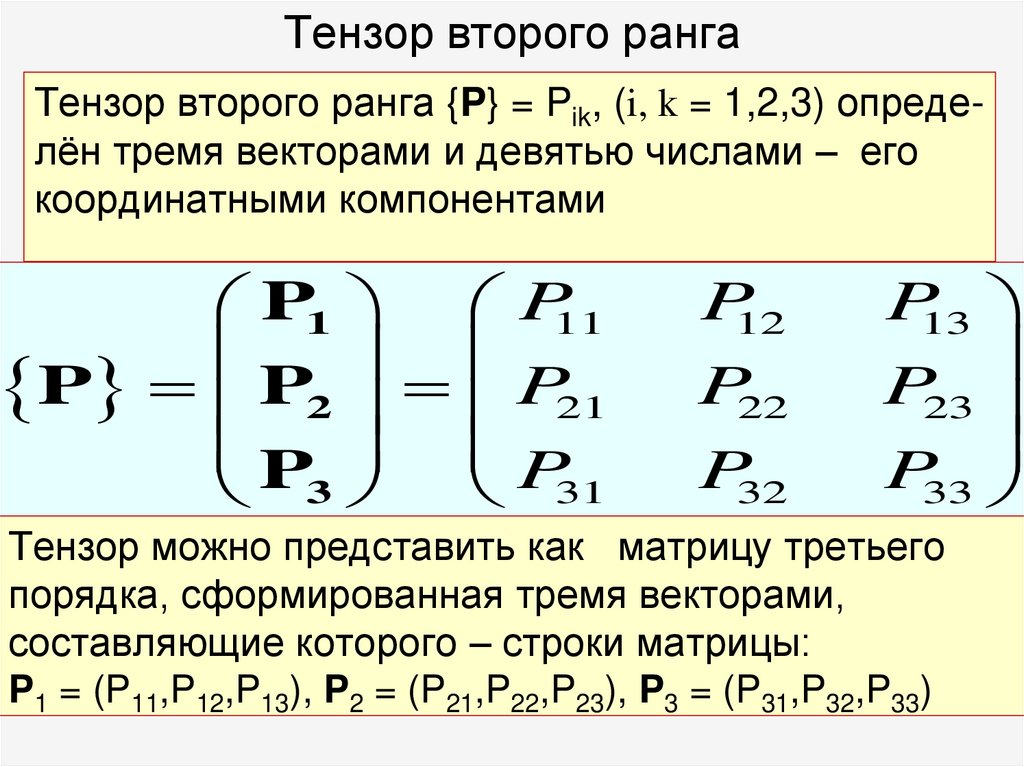
29. Тензор второго ранга

Тензор второго ранга {P} = Pik, (i, k = 1,2,3) определён тремя векторами и девятью числами – его
координатными компонентами
P1 P11
P P2 P21
P P
3 31
P12
P22
P32
P13
P23
P33
Тензор можно представить как матрицу третьего
порядка, сформированная тремя векторами,
составляющие которого – строки матрицы:
P1 = (P11,P12,P13), P2 = (P21,P22,P23), P3 = (P31,P32,P33)

30. Транспонированный тензор

Транспонированный тензор {Pт} тензора {P} , у
которого элементы отражены симметрично
относительно диагонали: Pтik = Pki:
P11
P
P
21
P
31
P12
P22
P32
P13
P23
P33
P11
T
P P12
P
13
P21
P22
P23
P31
P32
P33

31. Симметричный и антисимметричный тензоры

Симметричный тензор {PS}:
симметричные
относительно диагонали
компоненты равны
PSik = PSki;
P11
PS P12
P
13
P12
P22
P23
Антисимметричный тензор
{PA}: диагональные элементы PAii = 0, симметричные
относительно диагонали
компоненты имеют разные
знаки: PAik = -PAki
P0
ik = -Pki P
P
P13
P23 PA P12
P
P33
13
12
0
P23
P23
0
13
Произвольный тензор {P} = Pik разлагается на сумму
симметричной и антисимметричной частей:
{P} = { PS } + { PA }, { Ps}: PSik = PSki, { PA}: PAik= - PAki

32. Разложение произвольного тензора { P} = Pik на симметричную { PS} и антисимметричную {PA} части: {P} = {PS} + {PA}

P11 P12
P P
P
21 22
P P
31 32
P13
1
1
T
P23 P P P PT PS PA
2
2
P33
P12 P21 P13 P31
2 P11
1
PS P12 P21 2 P22 P23 P32 ;
2
P
P
P
P
2
P
33
13 31 23 32
0
1
PA P21 P12
2
P31 P13
P12 P21
0
P32 P23
P13 P31
P23 P32
0

33. Тензор диады – тензорное произведение векторов

Для векторов a и b существуют три вида умножений: скалярное s = a ∙ b, v = a ∙ b и диада,
{D} = a ● b, Dik = aibk, - тензорное произведение
векторов a = (a1,a2,a3) и b =(b1,b2,b3):
D11
D D21
D
13
D12
D22
D23
D13 a1b1
D23 a2b1
D33 a3b1
a1b2
a2b2
a3b2
a1b3
a2b3 Ds Da
a3b3

34. Симметричная и несимметричная части диады {D}

D Ds Da
a1b2 a2b1 a1b3 a3b1
2a1b1
1
2a2b2
a2b3 a3b2
Ds a1b2 a2b1
2
a
b
a
b
a
b
a
b
2
a
b
2 3
3 2
3 3
13 31
0
a1b2 a2b1 a1b3 a3b1
1
0
a2b3 a3b2
Da a2b1 a1b2
2
a
b
a
b
a
b
a
b
0
3 2
2 3
31 13

35. Антисимметричная часть диады {Da}

Антисимметричная часть диады {Da} состоит из
компонент векторного произведения производящих векторов c = [a, b]
0
a1b2 a2b1 a1b3 a3b1
1
0
a2b3 a3b2
Da a2b1 a1b2
2
a
b
a
b
a
b
a
b
0
31 13 3 2 2 3
c3 c2
0
1
c3 0
c1
2
c
c
0
1
2
c a b e1 (a2b3 a3b21 ) e2 (a3b1 a1b3 ) e3 (a1b2 a2b1 )

36. Внутреннее умножение вектора V = Vi на тензор {P}= Pik

Вектор умножается на тензор слева ({Π = V∙{P}) или
справа (Π* = {P} ∙ V) в соответствии с формулами:
k V P k Vi Pik ,
i
k P V k Vi Pki V Т P
Π V P PT V ,
i
Π P V V PT
V1 P11 P12 P13 V1P11 V2 P12 V3 P13
V P V P V P
Π V2
P
P
P
22
23
2 22
3 23
21
1 21
V P
3 31 P32 P33 V1P31 V2 P32 V3 P33
P11 P12 P13 V1P11 V2 P21 V3 P31
Π V1 ,V2 ,V3 P21 P22 P23 V1P12 V2 P22 V3 P32
P
V P V P V P
P
P
31
32
33
2 23
3 33
1 13
Результаты умножения – векторы Π и Π*

37. Умножение вектора d = di на диаду {D} = a●b

Произведение вектора на тензор это умножение
вектора на матрицу. Разложим диаду на
симметричную и несимметричную составляющие :
Π d D d ( Ds Da )
Из симметрии первого слагаемого получим:
d D s D s d d D D d
s
s
Для второго слагаемого:
1
1
d D D d c d a b d, c a b
2
2
c e1 (a2b3 a3b21 ) e2 (a3b1 a1b3 ) e3 (a1b2 a2b1 )
a
a

38. Инварианты тензора {P}= Pik относительно линейных преобразований координат

Инвариант – это функция элементов тензора, которая
не меняется при линейных преобразованиях координат
Инвариант 1: След тензора - сумма диагональных
элементов:
J1 P11 P22 P33 3 p
Инвариант 2: Квадрат тензора:
J 2 P P Pik2
i ,k
Инвариант 3: Детерминант тензора:
P11
J 3 det P P21
P31
P12
P22
P32
P13
P23
P33

39. Разложение тензора внутренних напряжений {P} на сферическую и девиаторную часть

С помощью первого инварианта можно получить разложение :
P11
P P21
P
31
P12
P22
P32
J1
0
0
P13
(s)
(d )
P23 J1 E P J1 E P P
P33
0 0 P11 J1
P12
P13
J1 0 P21
P22 J1
P23
0 J1 P31
P32
P33 J1
Первое слагаемое {Ps} сферически симметричное (p = -J1/3
– давление), второe {Pd} – тензор сдвиговых напряжений,
который описывает отклонение {P} от этой симметрии.

40. Главные оси и главные значения симметричного тензора {S}

Векторы по главным осям тензора {S} не
меняют направления в пространстве при
линейном преобразовании координат.
Если е = (е1,е2,е3) единичный вектор вдоль
такой оси, он должен удовлетворять уравнению:
S e e S E e 0
λ – собственные значения тензора {S}

41. Уравнение для собственных значений симметричного тензора {S}

S11 e1 S12e2 S13e3 0
S12e1 S22 e2 S23e3 0
S13e1 S23e2 S33 e3 0
Для нетривиального решения детерминант системы
обращается в ноль и получаем уравнение для собственных
значений λ
S11
S12
S13
S12
S 22
S23
S13
S 23 0
S33

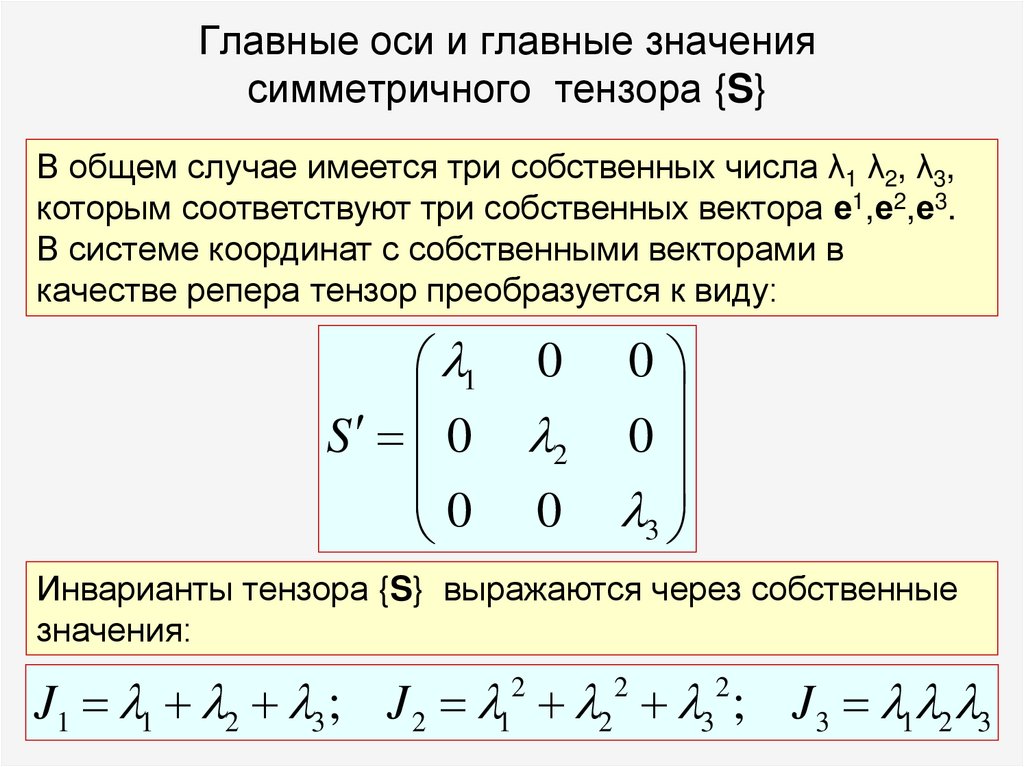
42. Главные оси и главные значения симметричного тензора {S}

В общем случае имеется три собственных числа λ1 λ2, λ3,
которым соответствуют три собственных вектора е1,е2,е3.
В системе координат с собственными векторами в
качестве репера тензор преобразуется к виду:
1 0
S 0 2
0 0
0
0
3
Инварианты тензора {S} выражаются через собственные
значения:
J1 1 2 3 ; J 2 2 3 ; J 3 1 2 3
2
1
2
2

43. Дифференциальные операции со скалярами, векторами и тензорами

Дифференцирование скалярного φ и векторного V
полей. Дифференцирование тензорного поля {Р}. Дифференциальные операторы в декартовых координатах.
Алгебра дифференциальных операторов. Дифференцирование векторных полей. Декартовы координаты (x,y,z)
с единичными векторами i, j, k: Дифференциальная
диада поля скорости V, симметричная и несимметричная части.
43

44. Тензор диады – тензорное произведение векторов

Для векторов a и b существуют три вида умножений: скалярное s = a ∙ b, v = a ∙ b и диада,
{D} = a ● b, Dik = aibk, - тензорное произведение
векторов a = (a1,a2,a3) и b =(b1,b2,b3):
D11 D12 D13 a1b1 a1b2 a1b3
D D21 D22 D23 a2b1 a2b2 a2b3 Ds Da
D
a b a b a b
D
D
23
33
3 2
3 3
13
31
Введение вектора дифференцировая
1 1 1
,
,
h1 x1 h2 x2 h3 x3
Позволяет достаточно просто проводить дифференциальные операции с разными переменными, включая тензоры.

45. Дифференцирование скалярного φ и векторного V полей

Все операции дифференцирования определены как
пределы отношений интегралов по поверхности σ,
ограничивающей объем → 0 (n – внешняя нормаль к σ):
1 1 1
1
,
,
n d ,
, grad lim
0
h1 x1 h2 x2 h3 x3
1
1
divV V lim n Vd , rotV V lim n Vd
0
0
Векторная
производная
вектора
дифференциальной диады {DV} :
1
–
тензор
n Vd
DV GradV V lim
0

46. Дифференцирование тензорного {Р} поля, вектор дивергенции тензора

Векторная производная вектора V – тензор дифференциальной диады {DV} и транспонированная диада - градиент:
dV
1
dV
n Vd ; GradV
DV V lim
0
dR
dR
T
1 dV dV
S
2 dR dR
T
{S} – симметричная часть диады вектора скорости – тензор
скоростей деформаций. Вектор D дивергенции тензора {Р}:
D Div P P lim
0
1
n P d ,

47. Правила дифференцирования векторных полей

divV divV Vgrad , divrotV 0
rot V rotV grad V,
div V U =UrotV VrotU,
rot V U U V V U VdivU UdivV
grad V U U V V U V rotU U rotV
graddivV V V
Оператор конвективного переноса
1
1
2
2
V V V V V gradV V rotV
2
2

48. Дифференциальные операторы в декартовых координатах

Градиент скаляра, дивергенция d вектора V, ротор ω
вектора V: по повторяющимся индексам предполагается суммирование
e1 i, e2 j, e1 k ,
Vi Vi
V V1 ,V2 ,V3 i ei
eV
d divV
,
i i,
xi
xi
i xi
Vl Vk
Vl
ω rotV V i ikl
ei
i k l i
xk
k ,l
xk xl
i
x
u
j
y
v
k
V3 V2
V2 V1
V1 V3
e1
e2
e3
z
z
x
z
y
x y
w

49. Дифференциальные операторы в декартовых координатах

Дифференциальная диада {D} вектора V:
Vi
dV
D Dij
dR
x j
Вектор дивергенции D тензора {P}
Pki Pki
D Div P P i
xk
k xk
Здесь и далее предполагается, что по повторяющимся
индексам происходит суммирование

50. Декартовы координаты (x,y,z) с единичными векторами i, j, k

Дивергенция тензора {P}
Pik
T iT1 jT2 kT3 DivP P k
i xi
P11 P21 P31 P12 P22 P32
P13 P23 P33
i
j
k
x
y
z
x
y
z
x
y
z
Действия над векторами
V iu jv kw; i
j
k
x
y
z
u v w
divV
,
x y z
2 2 2
2 2 2
x
y
z
w v u w
v u
ω =rotV i
j
i x j y k z
k
50
y z z x
x y

51. Декартовы координаты Дифференциальная диада поля скорости V

u
x
u
DV V
y
u
z
v
x
v
y
v
z
w
x
w
S
A
y
w
z

52. Симметричная часть диады {S} – тензор скоростей деформаций поля скоростей V

u
2 x
1 u v
S
2 y x
u w
z x
v u
x y
v
2
y
v w
z y
w u
S 1 Vi Vk
ik
x z
2 xk xi
w v
, x1 x, x2 y, x3 z
y z
V1 u , V2 v, V3 w
w
z

53. Антисимметричная часть дифференциальной диады выражается через компоненты вектора вихря ω = rotV;

0
1 u v
A
2 y x
u w
z x
w u
x z
3 2
0
w v 1
0
3
0
1
y z 2
0
2
1
v w
0
z y
w v
u w
v u
ω rotV, 1
, 2
, 3
y z
z x
x y
v u
x y

54. Деформация поля вектора скорости V(x1,x2,x3)

Дифференциал вектора V имеет вид:
Vi
d V i dx j D ji dx j ( S ji Aji )dx j
j x j
j
j
1
d V S dR A dR S dR ω dR
2
Это соотношение описывает различие скоростей в соседних
точках. Здесь:
S тензор скоростей деформаций – симметричная часть
дифференциальной диады;
А – антисимметричная часть дифференциальной диады;
ω = rot V.
54
Первое слагаемое соответствует деформации поля, второе –
вращению с угловой скоростью Ω = 0,5 ω.

55. Криволинейные ортогональные координаты

x3,u3
Z
l0
x2,u2
e2
e1
e
3
x1,u1
X
b0
Y
c0
u(t)
X, Y, Z– декартовы координаты
x1, x2, x3 – криволинейные ортогональные координаты
e1, e2, e3 – орты криволинейных ортогональных координат
V1, V2, V3 – компоненты вектора скорости
hi(x1, x2, x3) – метрические коэффициенты (Ламэ)

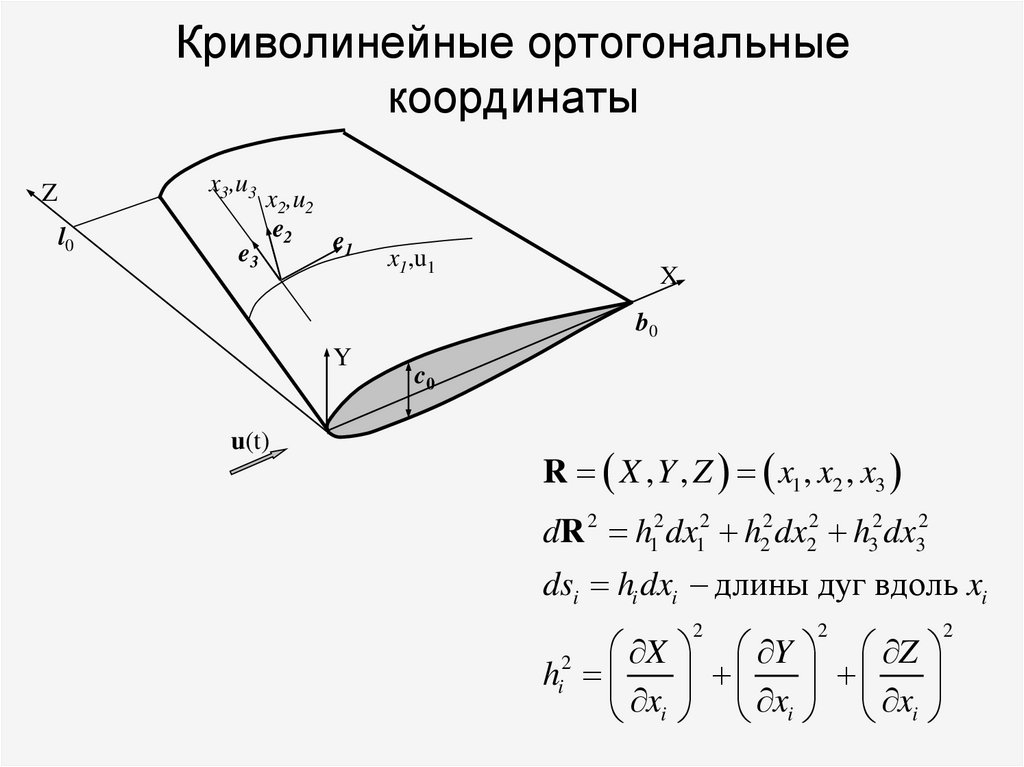
56. Криволинейные ортогональные координаты

x3,u3
Z
l0
x2,u2
e2
e1
e
3
x1,u1
X
b0
Y
u(t)
c0
R X , Y , Z x1 , x2 , x3
dR 2 h12 dx12 h22 dx22 h32 dx32
dsi hi dxi длины дуг вдоль xi
2
2
X Y Z
h
x
x
x
i i i
2
i
2

57. Алгебра дифференциальных операторов в ортогональных криволинейных координатах

Вектор дифференцирования (градиент) . По
повторяющимся индексам происходит суммирование
1 1 1
,
,
h1 x1 h2 x2 h3 x3
e1 e 2 e3
ei ei
,
h1 x1 h2 x2 h3 x3
hi xi
i hi xi
Вектор градиента скаляра φ
1 1 1
,
,
h1 x1 h2 x2 h3 x3

58. Алгебра дифференциальных операторов в ортогональных криволинейных координатах

Дивергенция вектора V, оператор Лапласа скаляра φ
1 h2 h3V1 h1h3V2 h1h2V3
divV V
h1h2 h3 x1
x2
x3
Опрератор Лапласа: divgrad 2
1 h2 h3 h1h3 h1h2
h1h2 h3 x1 h1 x1 x2 h2 x2 x3 h3 x3

59. Дифференциальная алгебра в криволинейных ортогональных координатах

e1 e2 e3
V e1u1 e2u2 e3u3 , grad
;
h1 x1 h2 x2 h3 x3
1 h2 h3 h1h3 h2 h1
;
h1h2 h3 x1 h1 x1 x2 h2 x2 x3 h3 x3
1 V1h2 h3 V2 h1h3 V3h2 h1
Q divV
h1h2 h3 x1
x2
x3
ω e1 1 e 2 2 e3 3 rotV
e1 V3h3 V2 h2 e2 V1h1 V3h3 e3 V2 h2 V1h1
h2 h3 x2
x3 h1h3 x3
x1 h1h2 x1
x2

60. Тензор скоростей деформаций в криволинейных ортогональных координатах

1 dV
S
GradV ;
2 dR
dV
D - дифференциальная диада D вектора скорости V
dR
T
dV
GradV
- транспонированная дифф. диада вектора скорости
dR
1 1 Vi 1 Vk
Vi kik Vk kki , i k ;
2 hk xk hi xi
Sik
1 Vi k V k V k V k V i k ;
ii i
i1 1
i2 2
i3 3
h x
k k
1 hi
kik
- кривизны координатных линий
hi hk xk

61. Дивергенция тензора {Р} в криволинейных ортогональных координатах

1 P11h2 h3 P21h1h3 P31h2 h1
Div P 1 h h h x x x
1 2 3
1
2
3
k12 P12 k13 P13 k21 P22 k31 P33
1 P21h2 h3 P22 h1h3 P23h2 h1
Div P 2 h h h x x x
1 2 3
1
2
3
k21 P21 k23 P23 k12 P11 k32 P33
P31 H 2 H 3 P32 H1 H 3 P33 H 2 H1
1
Div P 3 H H H x x x
1 2 3
1
2
3
k31 P31 k32 P32 k13 P11 k23 P22

62. Асимптотический подход к решению систем дифференциальных уравнений с малым параметром: сращиваемые асимптотические разложения

Найфэ A.Х. Введение в методы возмущений, М.: Мир,
1984. 535 с. Introduction to perturbation Techniques. J. Wiley
& Sons. New York, 1981
Дж.Д. Коул. Методы возмущений в прикладной
математике. М.: Мир. 1972.274 с.
М. Ван-Дайк. Методы возмущений в механике жидкости.
М.: Мир. 1967. 311 с.
62

63. Малые параметры в физике

lp= 10-33 cм – длина Планка определяет масштабы, когда
многоразмерность и закрученность физического
пространства становится очевидной
ae=2.82 · 10-13 cм – радиус электрона; на этих масштабах
структура электрона (кварки) важна
a0=h/(2πme2) = 0.529 ·10-8см – радиус Бора; на этих
масштабах важна структура атома
1/с =1/3 ·10-8s/m, c – скорость света; при таких скоростях
релятивистские эффектры важны
~ 10-5см – длина свободного пробега молекул в газе; на
таких масштабах важны молекулярные эффекты в газе
1/Re ~10-6-10-9 (Re – число Рейнольдса) – порядок
вязких членов в уравнениях Навье- Стокса
63

64. Разделы физики, определяемые малыми параметрами

r/lp = О(1) – Физика суперструн;
r/ae = О(1) – Физика кварков;
r /a0 = О(1) – Атомная физика
v/c = О(1) – Релятивисткая физика
r /a0 << /r = О(1) – Молекулярная физика,
кинетическая теория
/r << 1 – Сплошная среда, аэродинамика
1/Re << 1 – Теория пограничного слоя.
Последние две области – это наш курс!
64

65. Асимптотический анализ. Регулярные (внешнее) асимптотическое разложение

dy
Рассмотрим задачу
y 0, y 0 a, 1
dt
Решение ищем в виде ряда по малому параметру
y y0 t y1 t y2 t ... yn t ...
2
n
dy0
dy1
0, y0 t a;
y0 0, y1 t at ;
dt
dt
2
n
dy2
t
t
y1 0, y2 t a ; yn t a
dt
2
n!
t
y a
a exp t Это точное решение!!
n
n!
65

66. Малый параметр при старшей производной. Сингулярное асимптотическое разложение,

Задача Коши
dy
y 0,
dt
y 0 a, 1;
t
y a exp
Регулярное разложение не дает решения!
y y0 t y1 t 2 y2 t ... n yn t ...; all yn 0!
Попробуем вести новую переменную:
t
, y y ;
dy
y 0,
d
t
y a exp a exp
И снова получили точное решение!!
66

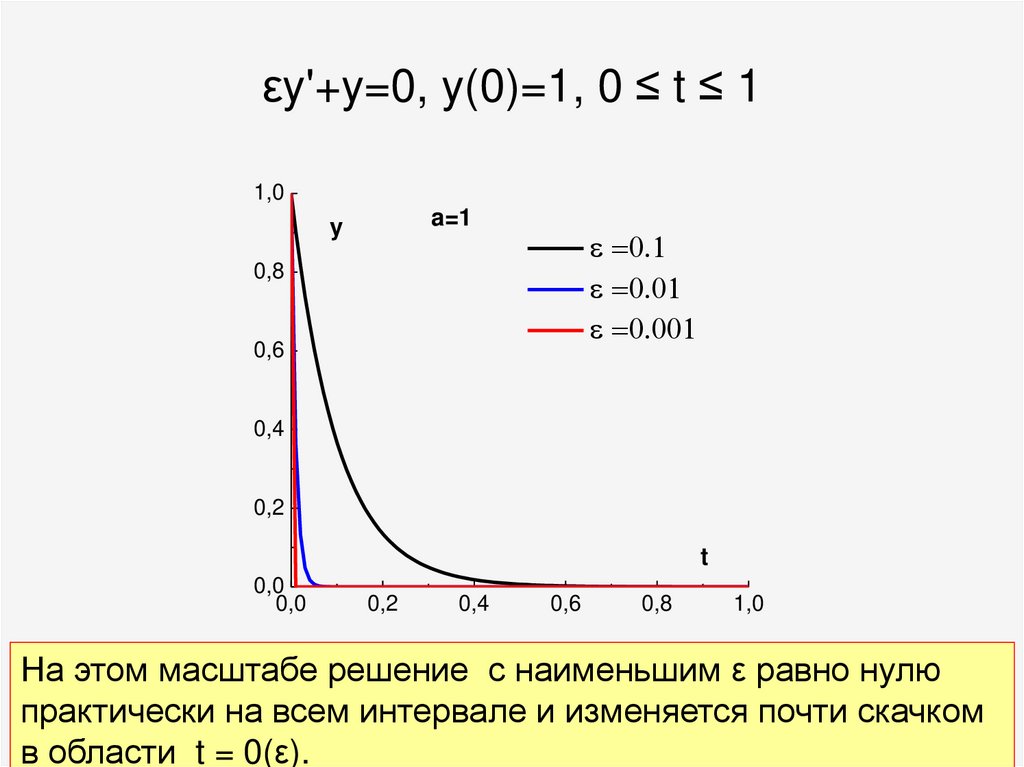
67. εy'+y=0, y(0)=1, 0 ≤ t ≤ 1

1,0
a=1
y
0,8
0,6
0,4
0,2
t
0,0
0,0
0,2
0,4
0,6
0,8
1,0
На этом масштабе решение с наименьшим ε равно нулю
практически на всем интервале и изменяется почти скачком
67
в области t = 0(ε).

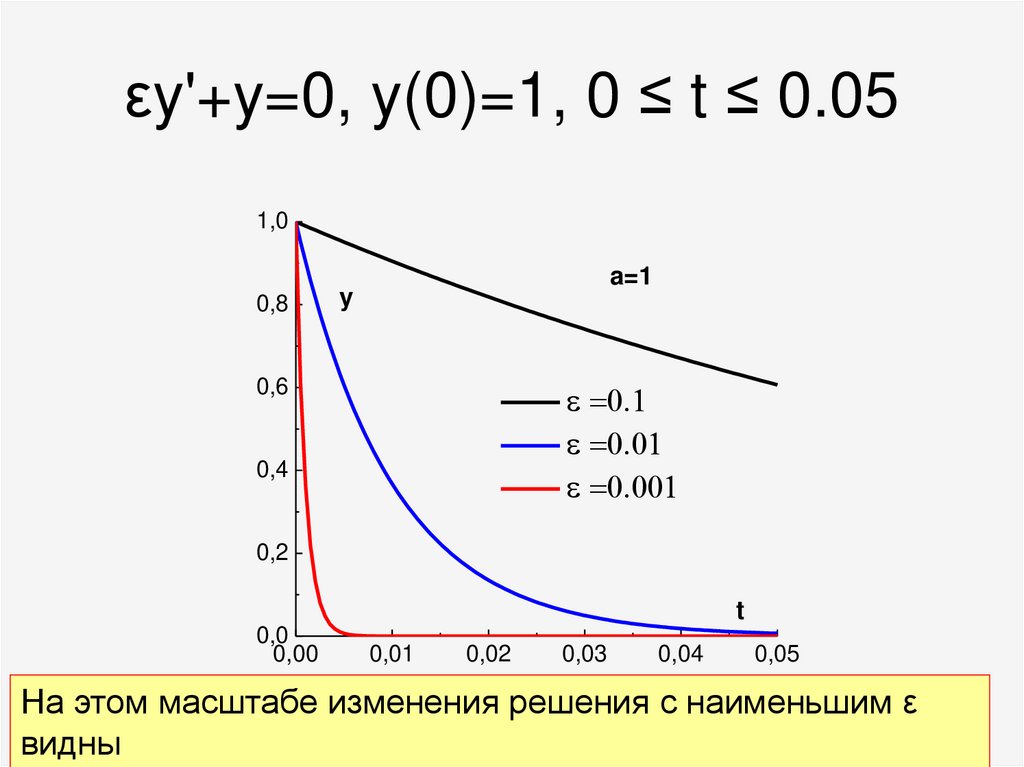
68. εy'+y=0, y(0)=1, 0 ≤ t ≤ 0.05

1,0
0,8
a=1
y
0,6
0,4
0,2
t
0,0
0,00
0,01
0,02
0,03
0,04
0,05
На этом масштабе изменения решения с наименьшим ε
видны
68

69. Двухточечная краевая задача

Постановка задачи
d 2T dT
2
0, T 0 a, T 1 b, 1;
dx
dx
Точное решение и его свойства в пределе ε→ 0
1
b a exp
x
a
b
T x, A exp B, A
, B
1
1
1 exp
1 exp
x 1
1
a
b
exp
b a exp
T x,
0
1
1 exp
1
x 1
b a exp
a O e
0
69

70. Двухточечная краевая задача. Асимптотическое решение

Регулярное (внешнее) разложение:
0 : T ( x) T0 ( x) T0 ( x) ... Tn ( x) ...
n
dT0
0, T0 a;
dx
2
dTn d Tn 1
, Tn 0
2
dx
dx
Сингулярное (внутреннее) разложение
x 1
, T x, t ; 0
d 2t
a, t 0 b
t
0,
t
2
d
0
t b a e a T x, 0 ,
70

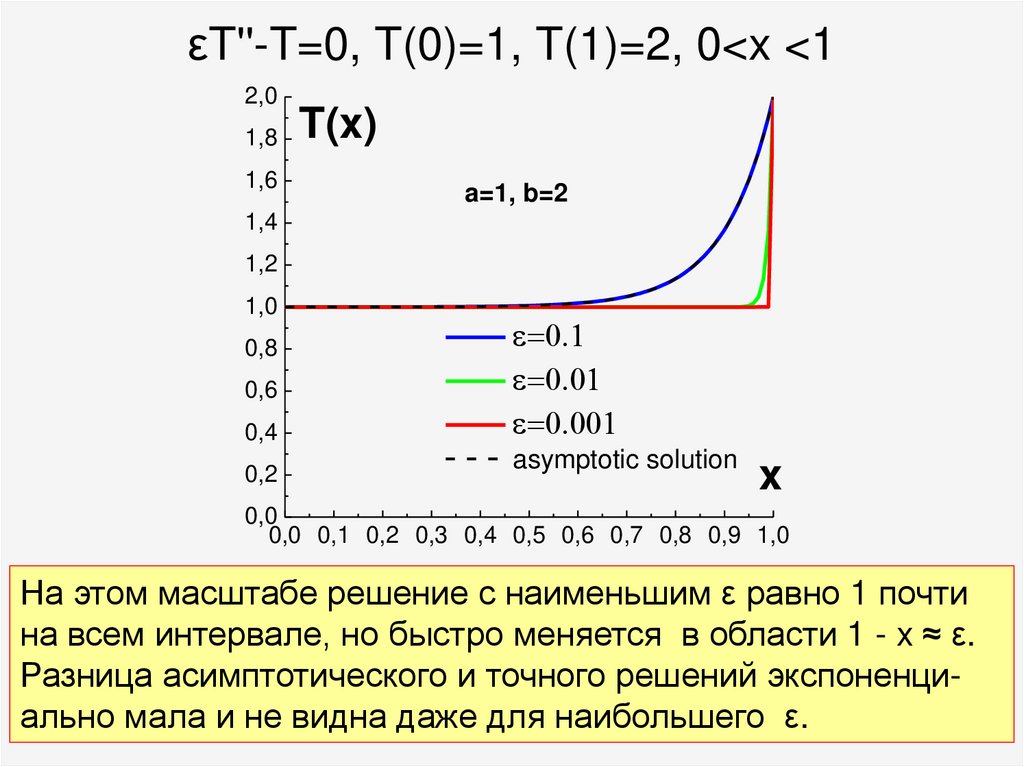
71. εT''-T=0, T(0)=1, T(1)=2, 0<x <1

εT''-T=0, T(0)=1, T(1)=2, 0<x <1
2,0
1,8
1,6
T(x)
a=1, b=2
1,4
1,2
1,0
0,8
0,6
0,4
0,2
asymptotic solution
x
0,0
0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0
На этом масштабе решение с наименьшим ε равно 1 почти
на всем интервале, но быстро меняется в области 1 - x ≈ ε.
Разница асимптотического и точного решений экспоненци71
ально мала и не видна даже для наибольшего ε.

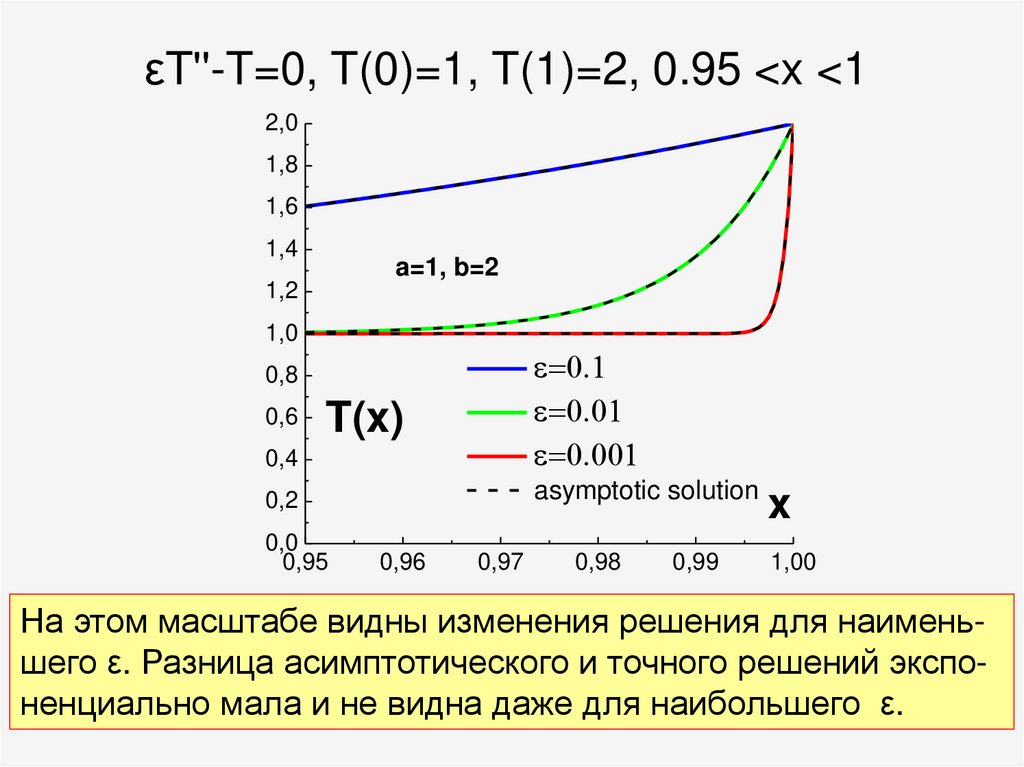
72. εT''-T=0, T(0)=1, T(1)=2, 0.95 <x <1

εT''-T=0, T(0)=1, T(1)=2, 0.95 <x <1
2,0
1,8
1,6
1,4
a=1, b=2
1,2
1,0
0,4
0,2
asymptotic solution
0,8
0,6
T(x)
0,0
0,95
0,96
0,97
0,98
0,99
x
1,00
На этом масштабе видны изменения решения для наименьшего ε. Разница асимптотического и точного решений экспоненциально мала и не видна даже для наибольшего ε. 72

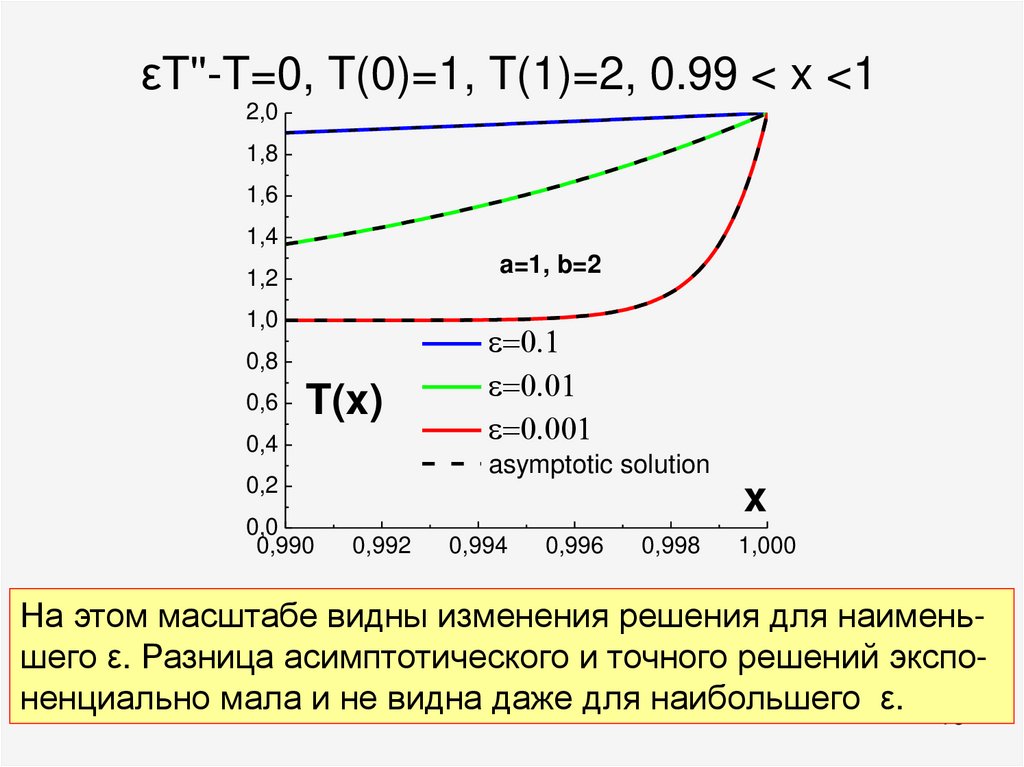
73. εT''-T=0, T(0)=1, T(1)=2, 0.99 < x <1

εT''-T=0, T(0)=1, T(1)=2, 0.99 < x <1
2,0
1,8
1,6
1,4
a=1, b=2
1,2
1,0
0,8
0,6
T(x)
0,4
asymptotic solution
0,2
0,0
0,990
x
0,992
0,994
0,996
0,998
1,000
На этом масштабе видны изменения решения для наименьшего ε. Разница асимптотического и точного решений экспоненциально мала и не видна даже для наибольшего ε. 73

74. Задача Коши для обыкновенного дифференциального уравнения (ОДУ) второго порядка. Асимптотическое решение

74

75. Постановка задачи Коши для ОДУ 2-го порядка с параметром ε << 1 при старшей производной

Постановка задачи Коши для ОДУ 2-го
порядка с параметром ε << 1 при старшей
производной
yxx p x y x q x y 0,
y 0 ,
p (0) 0, 1
yx 0
(1)
Можно решить это уравнение численно, но есть
вопросы с генерацией сетки: какого размера ее
делать для разных p(x) и q(x)? Равномерной или
нет?. Какая сетка оптимальна?
Ответы на эти вопросы можно найти, проведя
аналитическое исследование уравнения
асимптотическим методом.

76. Регулярное (внешнее) асимптотическое разложение

Интуитивным приближением для оценки
аналитического решения является использование
внешнего (регулярного) разложения по ε, которое
обозначим верхним индексом o:
y x; y x; y0 x y1 x ...
o
Этот ряд может включать бесконечный ряд членов.
76

77. Регулярный предел уравнения

Подставив это разложение в уравнение (1), получим:
y0 xx x y1xx x ...
p x y0 x x y1x x ...
q x y0 x y1 x ... 0
77

78. Уравнения внешнего разложения

При ε → 0, приравнивая члены с одинаковой
степенью ε, получим первые два уравнения:
p x y0 x q x y0 0,
y0 0 ,
p x y1x q x y1 y0 xx ,
y1 0 0, (2)
Уравнения имеют первый порядок и не позволяют
удовлетворить второму начальному условию для
производной.

79. Решение для главного приближения

В главном приближении решение уравнения (2)
имеет вид:
y0 x с0 e
R x
x
,
r x
R x r s ds
q x
0
p x
Удовлетворив краевому условию, получим:
y0 x e
R x

80. Внешнее решение второго порядка

Во втором приближении задача имеет вид:
p x y1x q x y1 e
R x
r x r 2 x ,
y1 0 0
Решение представляется так:
y1 x e
R x
x
ds
R x
r
s
r
s
0
p ( s ) с1e
2
c1 = 0 согласно начальному условию.
80

81. Внешнее решение

Двухчленное внешнее разложение имеет вид:
x
ds
R x
o
2
y x; e
1 r s r s
p s
0
Как видно, второе условие для производной не
может быть выполнено
81

82. Переменная пограничного слоя

Чтобы удовлетворить второму начальному условию, необходимо проанализировать область около
x = 0 более детально и попытаться сохранить вторую производную. С этой целью введем переменную около x = 0 и разложим коэффициенты p(x) и
q(x) в ряды Тэйлора около x = 0 :
x
,
x
p ( x) p ( ) p0 p1 ...,
q ( x) q ( ) q0 q1 ...

83. Сингулярное (внутреннее) разложение

Подставим коэффициенты в исходное уравнение
вместе с новой переменной:
y p0 p1 y q0 q1 y 0
y x; y i ; Y0 Y1 ..., and 0,
1 2
y x y
yxx 2 y 2
Y Y ...,
Y Y ..., (3)
0
0
1
1

84. Формулировка внутренней (сингулярной) задачи

Прежде всего рассмотрим случай p0 0. Тогда наибольшие
члены пропорциональны ε- и ε1-2 . Приравнивая эти
величины, получим:
1 2 1
y p0 y p1 y q0 q1 y
y x; y i ; Y0 Y1 ...,
y x x;
1
1
y ; Y0 Y1 ...
i
Y0 p0Y0 0, Y0 0 0; Y0 y0 0 условие сращивания
Y1 p0Y1 p1 Y0 q0Y0
Y1 0 0; Y1 0
(3)

85. Решение внутренней задачи первого порядка

Уравнение первого порядка имеет решение:
Y0 C0 e p0 C1 ;
C0 = 0 из-за первого условия. C1 = вследствие условия
сращивания. Итак, внутреннее решение 1-го порядка
имеет вид:
Y0 , Y0 0
Задача второго порядка переформулируется так
Y1 p0Y1 q0 ; Y1 0 0;
y x 0 Y1 0

86. Внутреннее решение второго порядка

Первый интеграл уравнения
q0
q0 p0
Y1
e ;
p0
p0
Решение принимает вид:
q0
q0 p0
p0
Y1
1 e
p0
p0
(4)
Полное внутреннее решение из двух членов имеет вид:
q0
q0 p0
p0
y
1 e
p0
p0
i
(4)
86

87. Пределы решений

Рассмотри внутренний предел внешнего решения yoi:
y oi x; lim y o x;
x 0
q0
ds
R
2
2
lim e
1
r
s
r
s
x
O
p( s)
0
p0
0
Рассмотрим внешний предел внутреннего решения уio:
q0
q0 p0
p0
y ;
1 e
p0
p0
q0
q0 p0
q0
io
i x
y ; lim y ;
x
0
p0
p0
p0
i
В главном приближении оба предела совпадают. Различие87
может быть исключено анализом 3-го приближения.

88. Композитное решение в главном приближении

Чтобы описать решение во всей области одной формулой
сложим внешнее и внутреннее решения и вычтем их общий
предел
y x; y x; y ; y
c
o
i
oi
x;
Подставляя полученные решения в это выражение, найдем
формулу для композитного решения, описывающего течение
на всем отрезке:
x
q0 p0
ds
R x
y c x; e 1 r s r 2 s
1 e p0
p( s)
p0
0

89. Случай p(x) = x. Двухслойное разложение

yxx xyx y 0, y 0 , yx 0 (1)
Во-первых, рассмотрим внешнее решение:
y x; y0 x y1 x ...
xy0 x y0 0,
y0 0 ,
c0
y0
x
Решение конечно на всем отрезке, если: c0 =y0 = 0. Аналогично, этот же результат справедлив для всех приближений: yn =
yo(x;ε) = 0. Введем новую переменную:
x
,
y 0 ;
y y y y y 0;
y 0

90. Внутреннее разложение

В этом случае решение в пограничном слое дает полное решение задачи, y(x;ε) = yi(x;ε) . Малый параметр в уравнении
пограничного слоя отсутствует, но входит во второе краевое
условие. Решение представим разложением:
y x; y ; Y0 Y1 ...,
i
В результате задача подразделяется на две упрощенных
подзадачи
Y0 Y0 0, Y0 0 ; Y0 0 0
Y1 Y1 ; Y1 0 0; Y1 0
90

91. Решение

2
2
t2
2
Y0 e 2 ; Y1 e 2 e dt
0
x
2
2
x
x
2
t2
2
2
y x; Y0 Y1 e 2 e
e dt
0
В этом случае, это есть полное решение внутренней и
внешней задач, все остальные члены Yn = 0 для n > 1.

92. Поведение при →∞ (ε→0)

Поведение при →∞ (ε→0)
Рассмотрим поведение этой функции при →∞ - внешний
предел. Для этого преобразуем внутренний интеграл:
s
2
s0
s
x
t
t
t2
s ; F s e dt e dt e dt F s0 F s F s0
2
0
0
s0
2
2
Здесь
s
s t2
t2
2
1
e
e
F s F s0 et dt
2 dt
2 t
t
s0
s
0
s0
s
s2
e 1
1
3
3 5 ... F s0
2 s 2s
4s

93. Поведение при →∞ (ε→0)

Поведение при →∞ (ε→0)
s
s t2
t2
2
1
e
e
F s F s0 et dt
2 dt
2 t
t
s0
s0
s
0
s
s2
s
s2
e 1
1
3
e 1
1
3
3 5 ... F s0
3 5 ...
2 s 2s
4s
2 s 2s
4s
s0
Таким образом, при →∞ решение ведет себя так:
x2
2
3
y x;
1 2 4 ... e 2 0
x
x
x
Это означает, что внешний предел внутреннего решения
совпадает с внешним решением.