Похожие презентации:
5. предел
1. Предел последовательности
2.
ПоследовательностьОпределение 1.
Функцию вида у= f (х), х ϵ Ν называют
функцией натурального аргумента или
числовой последовательностью и
обозначают у = f (n) или у1, у2, у3,…, уn,…,.
3.
Способы задания числовойпоследовательности
1. Словесный способ.
Правила задания последовательности
описываются словами, без указания формул
или когда закономерности между
элементами последовательности нет.
Пример 1. Последовательность простых чисел:
2,3,5,7,11,13,17,19,23,29,31,… .
Пример 2. Произвольный набор чисел:
1,4,12,25,26,33,39,… .
Пример 3. Последовательность четных чисел:
2,4,6,8,10,12,14,16,… .
4.
Способы задания числовойпоследовательности
2. Аналитический способ.
Любой n-й элемент последовательности
можно определить с помощью формулы.
Пример 1. Последовательность четных чисел: у = 2n.
Пример 2. Последовательность квадратов натуральных чисел:
у = n².
Пример 3. Последовательность у = n² - 3n
– 2, -2,0,4,10,…
Пример 4. Последовательность у = 2ⁿ
2, 2²,2³,…,2ⁿ,…
5.
Способы задания числовойпоследовательности
3. Рекуррентный способ.
Указывается правило, позволяющее вычислить
n-й элемент последовательности, если
известен ее предыдущий элемент.
Пример 1. a1 = 3 an+1 = аn2
a1=3
a3 = 92 = 81
a2 = 32 = 9
a4 = 812 = 6561
Пример 2. Арифметическая прогрессия аn+1= аn+d,
d - разность арифметической прогрессии.
Пример 3. Геометрическая прогрессия bn+1= bnq,
q – знаменатель геометрической прогрессии.
6.
Примеры последовательностей.Продолжите ряд: 1, 10, 3, 9, 5, 8, 7, 7, 9, 6…
Ответ: Ряд состоит из двух частей: числа на нечетных
местах: 1, 3, 5, 7, 9...; числа на четных местах: 10, 9, 8, 7
Продолжите ряд 77, 49, 36, 18…
Ответ: Перемножаются две цифры, входящие
в предыдущее число
7.
Числа Фибоначчи.1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610…
Элементы числовой последовательности, в
которой каждое последующее число равно сумме
двух предыдущих чисел.
Леонардо Фибоначчи - итальянский
математик.
(родился около 1170 — умер после 1228),
Последовательность Фибоначчи рекуррентно
задать легко, а аналитически – трудно.
n
n
1
1 5
1 5
xn
5 2 2
8.
Определение 2.Последовательность (уn), называют
ограниченной сверху, если все ее члены не
больше некоторого числа.
Последовательность (уn) ограничена сверху,
если существует число М такое, что для любого n
выполняется неравенство уn ≤ М. Число М
называют верхней границей
последовательности.
Например: -1, -4, -9, -16,…, - n²
Верхняя граница: -1
,…
9.
Определение 3.Последовательность (уn), называют
ограниченной снизу, если все ее члены не
меньше некоторого числа.
Последовательность (уn) ограничена снизу, если
существует число m такое, что для любого n
выполняется неравенство уn ≥ m. Число m
называют нижней границей
последовательности.
Например: 1, 4, 9, 16,…,n²,…
Нижняя граница: 1
10.
Если последовательность ограничена и снизу исверху, то ее называют ограниченной
последовательностью.
Ограниченность последовательности
означает, что все члены последовательности
принадлежат некоторому отрезку.
0
1
1 11 1
12 6 4 3
1
2
х
уn=
- ограниченная последовательность
уn ∈ [0;1]
11.
011 1 1
12 6 4 3
1
2
x
1
уn=
- ограниченная последовательность
Члены последовательности (уn) как бы
«сгущаются» около точки 0. Говорят
последовательность (уn) сходится.
yn = 2n - 1
01
3 5
7
9 11 13
x
У последовательности (уn) такой «точки
сгущения» нет. Говорят последовательность
(уn) расходится.
12.
Определение 4.Число a называют пределом
последовательности (уn), если в любой
заранее выбранной окрестности точки a
содержатся все члены последовательности,
начиная с некоторого номера.
yn а
lim
y
n= а
n→ ∞
Читают: предел последовательности (уn) при
стремлении n к бесконечности равен a.
13.
011 1 1
12 6 4 3
1
2
1
уn=
Члены последовательности (уn) как бы
«сгущаются» около точки 0.
Последовательность (уn) сходится.
1
0
Lim
n n
x
14.
Lim (2n 1)yn = 2n - 1
01
3 5
n
7
9 11 13
У последовательности (уn) такой «точки
сгущения» нет. Последовательность (уn)
расходится.
x
15.
Обсудимрезультаты,
полученные
в
примерах с геометрической точки зрения. Для
этого построим графики последовательностей:
1
yn ,
n
n
1
yn ,
2
2n
yn
.
n 1
16.
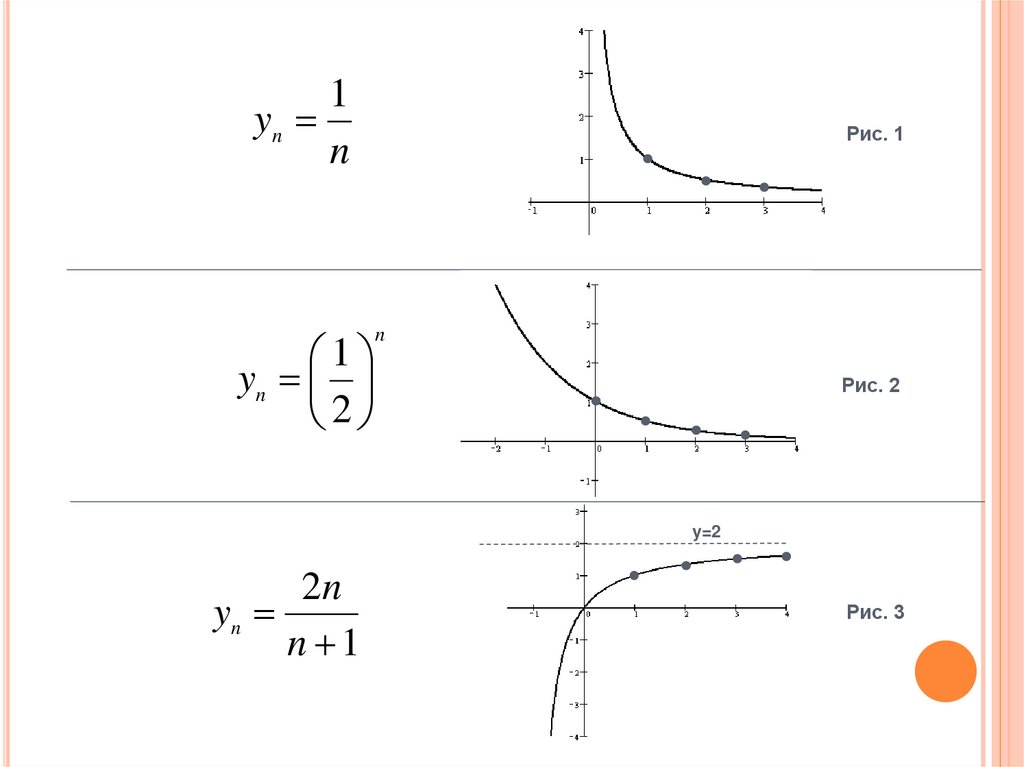
1yn
n
1
yn
2
yn
1
n
Рис. 1
n
Рис. 2
y=2
2n
yn
n 1
Рис. 3
17.
На всех трех рисунках точки графика,по мере их ухода вправо, все ближе и
ближе
подходят
к
некоторой
горизонтальной прямой:
на рис 1 – к прямой у=0,
на рис 2 – к прямой у=0,
на рис 3 – к прямой у=2.
Каждую
из
этих
прямых
называют
горизонтальной асимптотой графика.
18.
f ( n) blim
Равенство
означает,
n
что прямая y b является
горизонтальной асимптотой графика
последовательности,
графика функции
т.е.
yn f (n)
y=b
y f ( x ), x N .
19. Предел функции
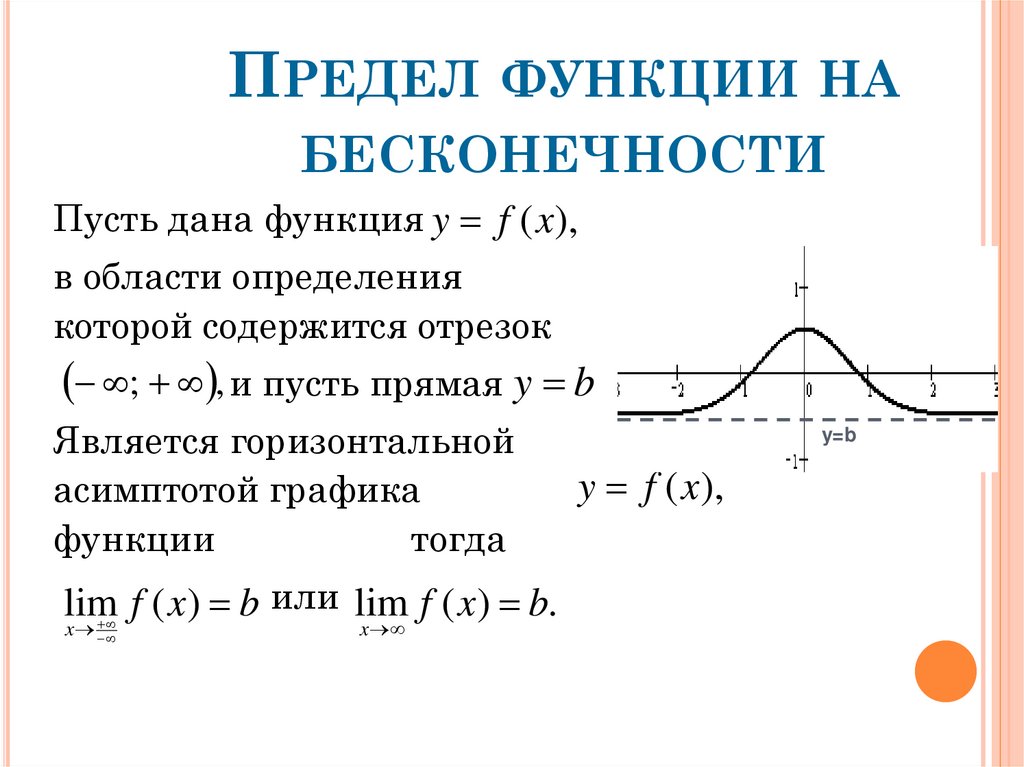
20. Предел функции на бесконечности
ПРЕДЕЛ ФУНКЦИИ НАБЕСКОНЕЧНОСТИ
Пусть дана функция y f (x),
в области определения
которой содержится отрезок
; , и пусть прямая y b
Является горизонтальной
асимптотой графика
функции
тогда
или lim f ( x) b.
lim
f
(
x
)
b
x
x
y=b
y f (x),
21. Свойства предела функции.
СВОЙСТВА ПРЕДЕЛА ФУНКЦИИ.1.
Для m N u k справедливо
соотношение
k
lim
0
m
x
x
22. 2. Если ,то
lim f ( x) b, lim g ( x) a2. ЕСЛИ x
x
,ТО
а) предел суммы равен сумме пределов:
lim ( f ( x) g ( x)) b a
x
б) предел произведения равен произведению
пределов:
lim ( f ( x) g ( x)) b a
x
23.
в) предел частного равен частному отпределов:
f ( x) b
lim
x g ( x )
a
г) постоянный множитель можно вынести
за знак предела:
lim kf ( x) kb
x
24.
Пример 1. Найти пределпоследовательности 1
yn
n
3.
Решение.
1
1
3 lim lim 3 0 3 3
lim
n n
n n
n
25.
Пример 2. Найти предел функцииРешение.
1
y 2
n
1
1
1
lim lim 0 0 0
lim
2
n n
n n
n n
26.
Пример 3. Найти предел функции5
y .
n
Решение.
5
1
1
lim 5 5 lim 5 0 0
lim
n n
n
n n
n
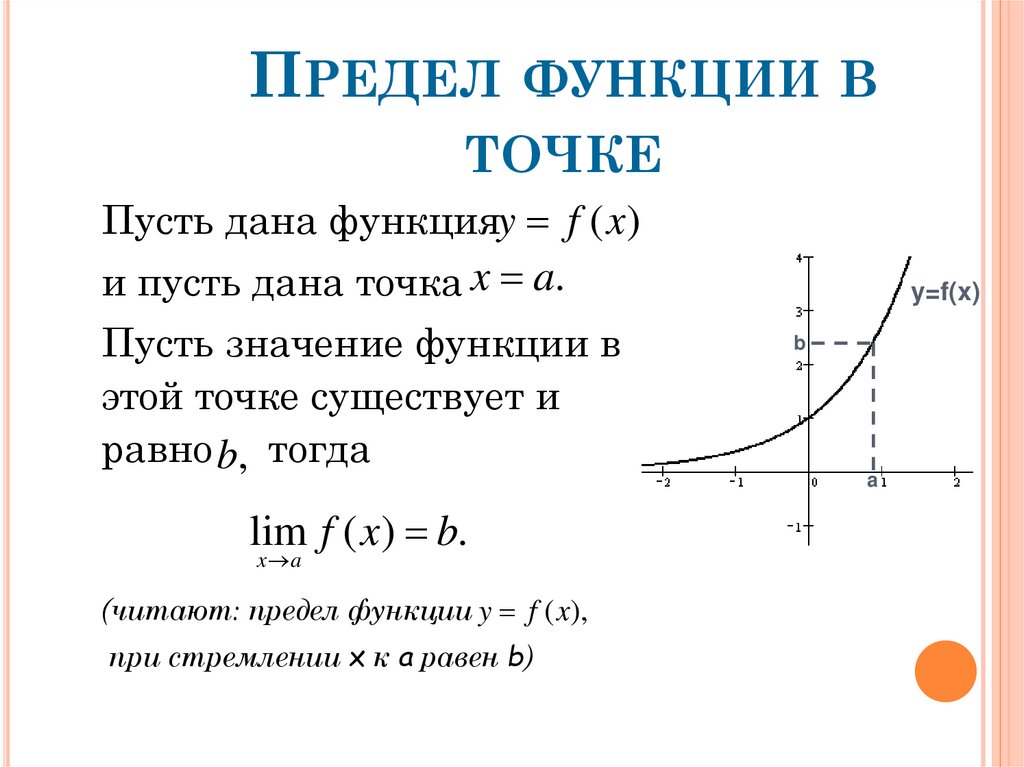
27. Предел функции в точке
ПРЕДЕЛ ФУНКЦИИ ВТОЧКЕ
Пусть дана функцияy f (x)
и пусть дана точка x a.
Пусть значение функции в
этой точке существует и
равно b, тогда
lim
f
(
x
)
b
.
x a
(читают: предел функции y f (x),
при стремлении х к а равен b)
y=f(x)
b
a
28. Пример 4. Вычислить
x2 9.
ПРИМЕР 4. ВЫЧИСЛИТЬ lim
x 3
4 x 12
Решение.
x 9
x 3 x 3
x 3 3 3
lim
lim
lim
1,5.
x 3 4 x 12
x 3
x 3 4
4 x 3
4
2
Ответ: -1,5.























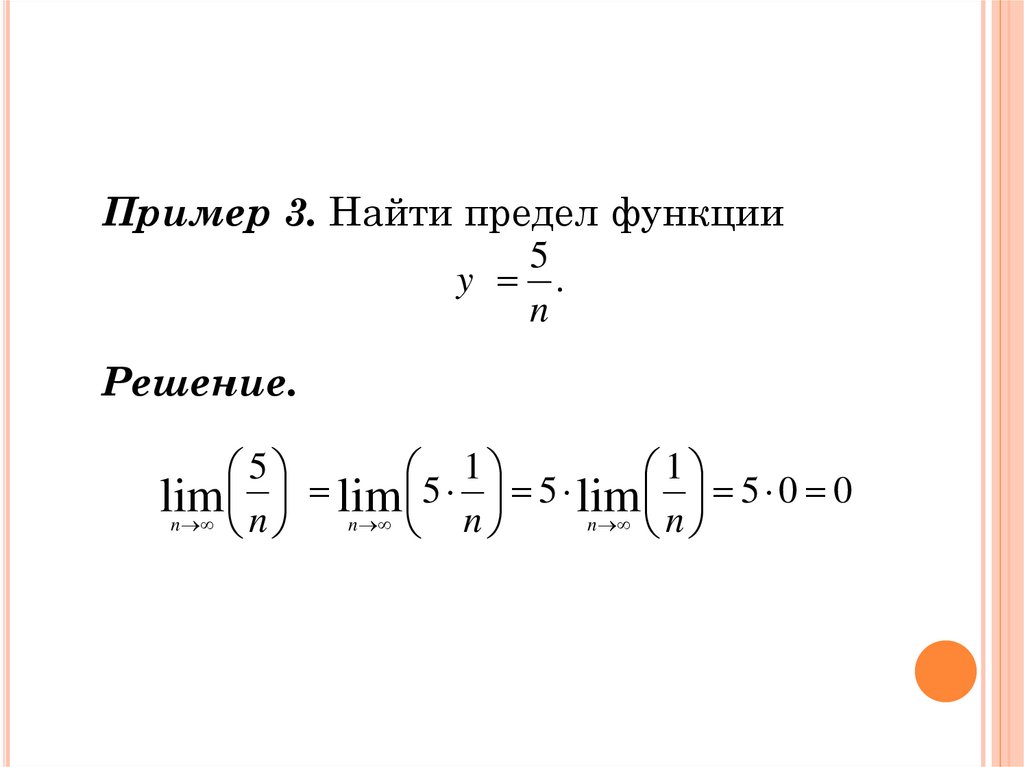

 Математика
Математика








