Похожие презентации:
1_Лекция 1-2
1.
М атем ати ческ и й анали зЦ е л ь и з у ч е н и я :о в л а д е н и е о с н о в н ы м и п о н я т и я м и и
п ред лож ен и ям и курса, м етод ам и д оказательства
утверж д ен и й , ум ен и ям и п ри м ен ять и зучен н ы е
оп ред елен и я и теорем ы к реш ен и ю зад ач и
д оказательству утверж д ен и й .
2.
3.
О сновная ли тература:1 . К у д р я в ц е в Л .Д . К у р с м а т е м а т и ч е с к о г о а н а л и з а . М .: В ы с ш а я
ш к о л а , Т .1 ,2 .– 2 0 0 2 .
2 . Ф и х т е н г о л ь ц Г .М . О с н о в ы м а т е м а т и ч е с к о г о а н а л и з а . С П б .:
Л ань, 2005.
3 . Б о х а н К .А . К у р с м а т е м а т и ч е с к о г о а н а л и з а . М и н с к : И н т е г р а л ,
2004.
4 . Б е р м а н Г .Н . С б о р н и к з а д а ч п о м а т е м а т и ч е с к о м у а н а л и з у .
С П б .: П р о ф е с с и я , 2 0 0 1 .
5 . Б р е й т и г а м Э .К ., В а р к е н т и н а Г .Т ., О д и н ц о в а Л .А . В в е д е н и е в
ан али з. Д и ф ф ерен ц и альн ое и счи слен и е д ля ф ун кц и й о д н ой
п е р е м е н н о й . Б а р н а у л : И зд -в о Б Г П У , 2 0 0 1 .
4.
Д ополни тельная ли тература:1 . Р у д и н У . О с н о в ы м а т е м а т и ч е с к о г о а н а л и з а С П б .: Л а н ь , 2 0 0 4 .
2 . И л ь и н В .А ., П о з д н я к Э .Г . О с н о в ы м а т е м а т и ч е с к о г о а н а л и з а .
М .: Н а у к а , Ч .I. – 1 9 8 2 , Ч .II. – 1 9 8 3 .
3 . И л ь и н В .А ., С а д о в н и ч и й В .А ., С е н ц о в В .Х . М а т е м а т и ч е с к и й
а н а л и з . М П У , Т .I. – 1 9 8 5 ; Т .II. – 1 9 8 7 .
4. Зад ачн и к п о курсу м атем ати ческого ан али за. П од ред .
Н .Я . В и л е н к и н а М .: П р о с в е щ е н и е , 1 9 7 1 , Ч .I-II.
5.
П о д ан н ом у курсу у вас б уд ут зан яти я д вух ви д ов: лекц и и ип ракти чески е зан яти я.
Н а лекц и ях б уд ете и зучать теорети чески й м атери ал,
зн аком и ться с об разц ам и вы п олн ен и я п ракти чески х зад ан и й с
и сп ользован и ем и зучен н ого м атери ала.
Н а п ракти чески х зан яти ях - реш ать зад ачи , д оказы вать теорем ы ,
которы е б ы ло п ред лож ен о и зучи ть сам остоятельн о.
6.
Д ля лекц и й и п ракти чески х зан яти й ц елесо об разн о завестиотдельны е тетради.
В тетрадях для лекций оставить больш ие поля для пояснений
к возн и кш и м воп росам , д ля вклеек с п оясн ен и ям и и
кон сп ектам и сам осто ятельн о и зучен н ого м атери ала.
7.
Н ад каж д ой лекц и ей след ует раб отать сразу п осле еепрослуш ивания:
1) разоб раться с введ ен н ы м и п он яти ям и , вы ясн и ть и х
сущ ествен н ы е п ри зн аки , п ри вести свои п ри м еры и кон трп ри м еры ;
8.
2) разоб рать д оказательства теорем , п ри вед ен н ы е н а лекц и ивы ясн и ть осн овн ы е этап ы д оказательства, все и сп ользуем ы е
в д оказательстве п ред лож ен и я, возм ож н ость и х и сп ользован и я;
3) д оказать теорем ы , п ред ло ж ен н ы е д ля сам остоятельн ого
и зучен и я; закон сп екти ровать; сд елать вкл ей ки в лекц и он н ы е
тетради.
9.
4) разоб рать об разц ы реш ен и я зад ач, об рати в особ ое вн и м ан и ен а и сп ользован и е и зучен н ы х оп ред елен и й и теорем д ля
обоснования реш ений.
П еред п ракти чески м зан яти ем остан ется п о втори ть
лекц и он н ы й и сам остоятельн о и зучен н ы й м атери ал.
10.
В п роц ессе п од готовки к п ракти ческом у зан яти ю н еоб ход и м о:1. П овтори ть зад ан н ы й теорети чески й м атери ал.
2. И зучи ть м атери ал, п ред лож ен н ы й д ля сам остоятельн ой
проработки;
3 . В ы п о л н и т ь п р а к т и ч е с к о е з а д а н и е , т .е . р е ш и т ь п р е д л о ж е н н ы е
для сам остоятельн ого вы п олн ен и я уп раж н ен и я.
11.
Р аздел 1.Д ействительны е числа и ф ункции
Г лава 1. Д ействительны е числа.
1§ .?1 Р а с ш и р е н и е п о н я т и я ч и с л а . Ч и с л о в ы е м н о ж е с т в а .
12.
П он яти е чи сла п рош ло д ли н н ы й п уть и стори ческого разви ти я.Н атуральн ы е чи сла как сред ство счета и звестн ы человеку н а
сам ы х ран н и х ступ ен ях разви ти я.
Д ревн егречески е м атем ати ки п ользовали сь как н атуральн ы м и ,
так и д роб н ы м и п олож и тельн ы м и чи слам и , н о н е зн али
отрицательны х чисел.
У потребление полож ительны х и отрицательны х чисел
толкуем ы х как «и м ущ ество» и «д олг» вп ервы е п ояви лось у
и н д у с о в ( А р ь я б х а т а р .4 7 6 г ., Б р а м а г у п т а 5 8 8 -6 6 0 г ., Б х а с к а р а р .
1 1 1 4 г .)
13.
С оврем ен н ое об озн ачен и е п олож и тельн ы х и отри ц ательн ы хч и с е л зн а к а м и « + » и « -» в в е д е н о в к о н ц е X IV в . н е м е ц к и м
м атем атиком В идм анном .
О д н ако ещ е в X V I в. м н оги е м атем ати ки н е п ри зн авали
отри ц ательн ы х чи сел. П олн ое п ри зн ан и е отри ц ательн ы е чи сла
п о л у ч и л и в X V II в .
14.
Т аки м об разом , д роб н ы е чи сла п ояви ли сь в м атем ати кезн ачи тельн о ран ьш е отри ц ательн ы х. В озн и кн овен и е д роб н ы х
чи сел связан о с зад ачам и и зм ерен и я.
Н атуральн ы е чи сла служ ат ф ун дам ен том , н а котором м огут
бы ть п остроен ы все други е чи словы е м н ож ества.
П оследовательно определяю тся целы е, рациональны е,
действительны е и ком плексны е числа.
15.
К аж дое из перечисленны х м нож еств содерж ит преды дущ иеN Z Q R C .
П ри этом стрем ятся построить расш ирение, обладаю щ ие
и звестн ы м и свой ствам и п о отн ош ен и ю к расш и ряем ом у
м нож еству.
16.
С ф орм улируем принцип расш ирения числового м нож ества.Е сли числовое м нож ество А , на котором определены те или
ины е операции и отнош ения, расш иряется до м нож ества В с
некоторы м и операциям и и отнош ениям и, то свойства
расш ирения сводятся к следую щ им :
17.
1 . М н о ж еств о А есть п о д м н о ж еств о В (A B - в к л ю ч ен и ес т р о го е , с о в п а д е н и й б ы т ь н е м о ж е т ).
2. И нтересую щ ие нас операции и отнош ения элем ентов
м нож ества А определены и для м нож ества В , причем их см ы сл
для элем ентов м нож ества А, рассм атриваем ы х уж е как
элем енты м нож ества В , долж ены совпадать с тем , которое они
им ели в А до расш ирения.
18.
3. В м нож естве В долж на бы ть вы полним а операция, которая вА бы ла не вы полним а.
4. Р асш и рен и е В д олж н о б ы ть м и н и м альн ы м и з всех возм ож н ы х
р а с ш и р е н и й м н о ж е с т в а А , о б л а д а ю щ и х с в о й с т в а м и 1 -3 , и
оп ред еляется д ан н ы м А од н озн ачн о с точн остью д о и зом о рф и зм а.
19.
Т ак м ы расш иряем м нож ество N до м нож ества целы х чисел Z ,а н е сразу д о д ей стви тельн ы х и ли ком п лек сн ы х.
N Z Q R C
П од роб н о с реали зац и ей п ри н ц и п а расш и рен и я и п остроен и я
м н ож еств N , Z , Q , R , C вы п озн аком и тесь в курсе «Ч и словы е
систем ы ».
20.
Ф ун д ам ен т м атем ати ческого ан али за составляет м н ож ество Rдей стви тельн ы х чи сел с оп ределен н ы м и н а н ем алгебраи чески м и
операциям и и отнош ением порядка. Э ти операции и
отн ош ен и е п орядка м огут бы ть сведен ы к оп ерац и ям слож ен и я
и у м н о ж е н и я и о т н о ш е н и ю « » м е н ь ш е .
В свою очередь все необходим ы е свойства последних м ож но
вы вести и з н еб ольш ого чи сла свой ств, п ри н яты х за акси ом ы .
21.
1§. ?2 . М н о ж е с т в о д е й с т в и т е л ь н ы х ч и с е лО п р е д е л е н и е . М н о ж е с т в о э л е м е н т о в x , y , z , ... н а з ы в а е т с я
м нож еством R действительны х чисел, если в нем установлены
следую щ ие операции и отнош ения, обладаю щ ие свойствам и:
22.
1 .О п е р а ц и я с л о ж е н и я : к а ж д о й п а р е э л е м е н т о в x , y п о с т а в л е н всоответстви е элем ен т z, н азы ваем ы й и х сум м ой и об озн ачаем ы й
x y такой, что вы полнены условия:
A 1 (к о м м у т а т и в н о с т ь с л о ж е н и я ):
x , y R x y y x ;
A 2 а с с о ц и а т и в н о с т ь с л о ж е н и я :
x , y , z R x y z x y z ;
A 3 с у щ е с т в о в а н и е н у л я :
0 R x R x 0 x ;
A 4 с у щ е с т в о в а н и е п р о т и в о п о л о ж н о г о э л е м е н т а :
x R y R x y 0 .
23.
2. О перация ум нож ения: каж дой паре x, y элем ентов из Rстави тся в соответстви е элем ен т u , н азы ваем ы й и х
п рои звед ен и ем , об озн ачаем ы й x y такой , что вы п олн яю тся
условия:
24.
M 1 (к о м м у т а т и в н о с т ь у м н о ж е н и я ):x , y R x y y x ;
M 2 а с с о ц и а т и в н о с т ь у м н о ж е н и я :
x , y R x y z x y z ;
M 3 су щ ест в о в ан и е ед и н и ц ы :
1 R x R x 1 x ;
M 4 с у щ е с т в о в а н и е о б р а т н о г о э л е м е н т а :
x 0 y R x y 1 ;
Л М x , y , z R x y z x z y z .
25.
3. О тнош ение порядка: для каж дой пары элем ентов x, y Rвы полняется хотя бы одно из соотнош ений x y или y x со
свойствам и:
O 1 x R x x ;
O 2 x , y R x y y x x y
26.
O 3 x , y , z R x y y z x z ;O 4 x , y R 0 x 0 y 0 x y ;
O A x , y , z R x y x z y z ;
O M
x , y , z R 0 z , x y x z y z ;
27.
Зам ечан и е 1. О тн ош ен и е x y, если x y зап и сы ваю т x y.O 3/ x , y , z R x y y z x z ;
x , y , z R x y x z y z ;
O M x , y , z R 0 z x y x z y z .
O A
Зам ечание 2. Е сли x y, то y x и наоборот.
28.
4. А ксиом а полнотын еп р ер ы в н о сти
Е сли Х и У непусты е подм нож ества R , обладаю щ ие тем
свой ством , что для лю бого x X и лю бого y Y вы п олн ен о
отнош ение x y, то сущ ествует c R такое, что x c y для
лю бы х x,y R.
29.
В заклю чен и е п араграф а остан ови м ся н а геом етри ческойинтерпретации действительны х чисел.
В геом етри и м н ож ество точек п рям ой вводи тся как
совокупность объектов, удовлетворяю щ их систем е аксиом ,
среди которы х ф ун дам ен тальн ую роль и грает акси ом а п олн оты .
30.
У п ом ян утая си стем а акси ом п озволяет устан ови тьвзаи м н оод н озн ачн ое соответстви е м еж д у м н ож еством R и
м нож еством точек прям ой.
Э то соответстви е п озволяет и зоб раж ать д ей стви тельн ы е чи сла
точкам и прям ой.
31.
В си лу взаи м н ой од н озн ачн ости соответстви я каж д ом удействительном у числу соответствует единственная точка
прям ой и каж дая точка прям ой является изображ ением
дей стви тельн ого чи сла.
Э то чи сло н азы ваю т ко орд и н атой точки .
32.
П рям ую , п ри н али чи и соответстви я, н азы ваю т чи словой п рям ой .В ви д у взаи м н ой од н озн ачн ости соответстви я сам о м н ож ество R
часто н азы ваю т чи словой п рям ой .
33.
§1 .?3 . Р а с ш и р е н н а я о б л а с т ь д е й с т в и т е л ь н ы х ч и с е л .Ч и сл овы е п р ом еж утк и .
Р асш и рен н ой об ластью д ей стви тельн ы х чи сел н азы вается
м нож ество R , полученное из R присоединением к нем у двух
сим волов и в качестве новы х элем ентов.
Н а эти сим волы распространяется отнош ени е порядка по
следую щ ем у правилу:
34.
1 . x R x ,2 . x R x ,
3 . .
, б еск о н еч н ы е эл ем ен ты м н о ж ества R , о стал ь н ы е
элем енты конечны .
35.
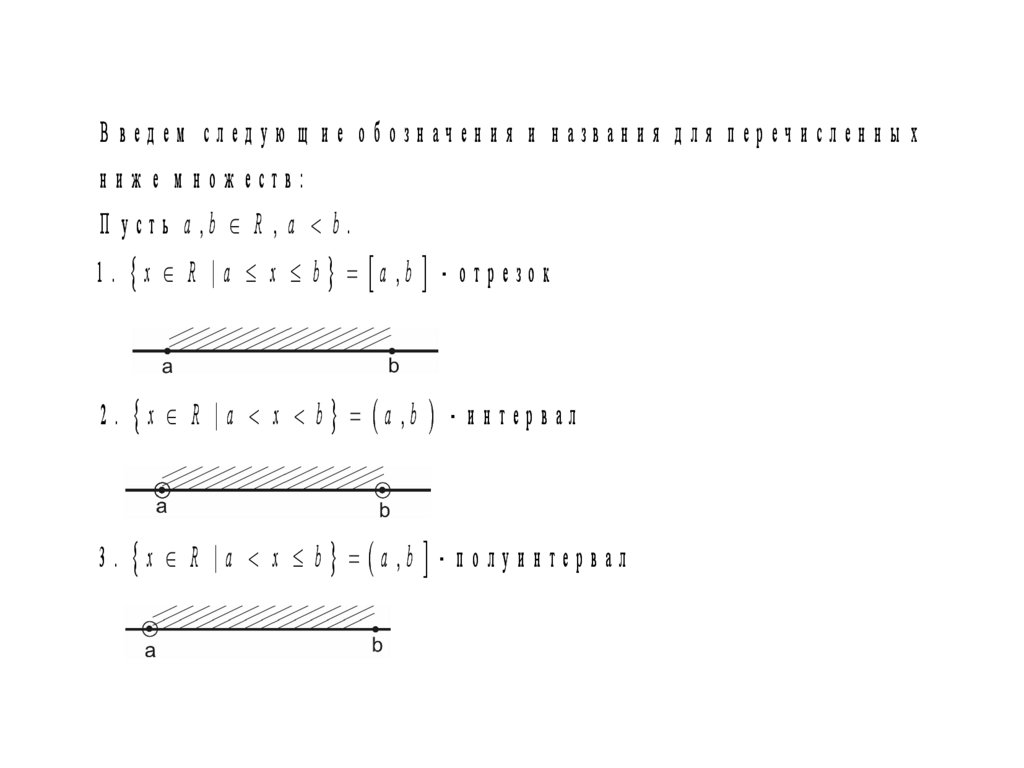
В вед ем след ую щ и е об озн ачен и я и н азван и я д ля п еречи слен н ы хниж е м нож еств:
П усть a ,b R , a b.
1 . x R | a x b a ,b - о т р е зо к
2 . x R | a x b a ,b - и н тер в ал
3 . x R | a x b a ,b - п о л уи н тер в ал
36.
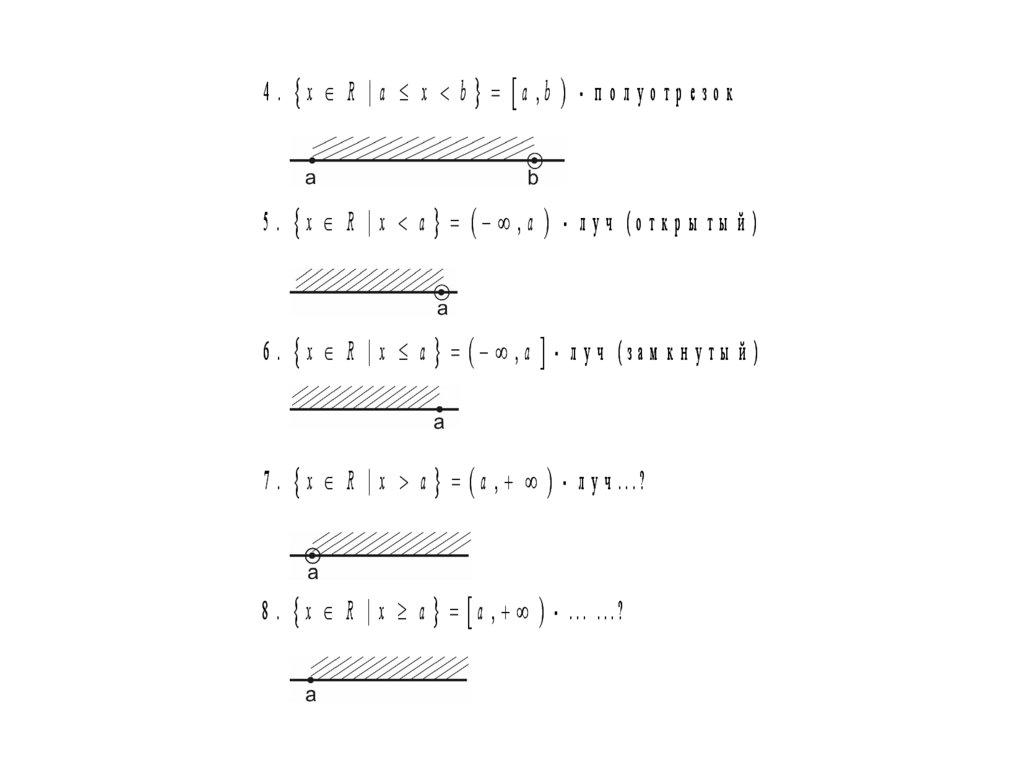
4 . x R | a x b a ,b - п о л у о т р е з о к5 . x R | x a ,a - л у ч (о т к р ы т ы й )
6 . x R | x a ,a - л у ч (за м к н у т ы й )
7 . x R | x a a , - л у ч ...?
8 . x R | x a a , - ... ...?
37.
9 . ; R ;1 0 . ; R .
О п ред елен и е. И н тервалы , отрезки , п олуи н тервалы , п олуотрезки
н азы ваю тся чи словы м и п ром еж уткам и .
38.
§1 ?. 4. М о д у л ь д е й с т в и т е л ь н о г о ч и с л аО п ред елен и е. М од улем д ей стви тельн ого чи сла x н азы вается
m a x a , a и о б о зн а ч а е т с я a .
a , есл и a 0,
Т аки м об разом , a
a , есл и a 0 .
39.
С войства м одуля:1 . x R x 0 ,
2 . x R x x ,
3 . x R x x ,
40.
4 . x , R x xД оказательство:
1. x 0 x x
2. x 0 x x
x x
x x x x
Т ак как x 0, получаем 0 x .
Т ак как x 0, получаем x 0.
И так , x x
41.
5 . x , R 0 x x ;6 . x , R x x x ;
Д оказательство:
1) x 0 x x x
2) x 0 x x;
x
x x x .
42.
7 . x , R x x x ;8 . x , a , R 0 x a a x a ;
9 . x , a , R 0 x a a x a ;
43.
1 0 . x , a , R x a x a x a ;1 1 . x , a , R x a x a x a ;
1 2 . x , y R x y x y ;
1 3 . x , y R x y x y .
44.
Г лава 2. Ф ункции2 .1 П о н я т и е ф у н к ц и и ( о т о б р а ж е н и я )
2 .1 .1 П о н я т и е с о о т в е т с т в и я
45.
46.
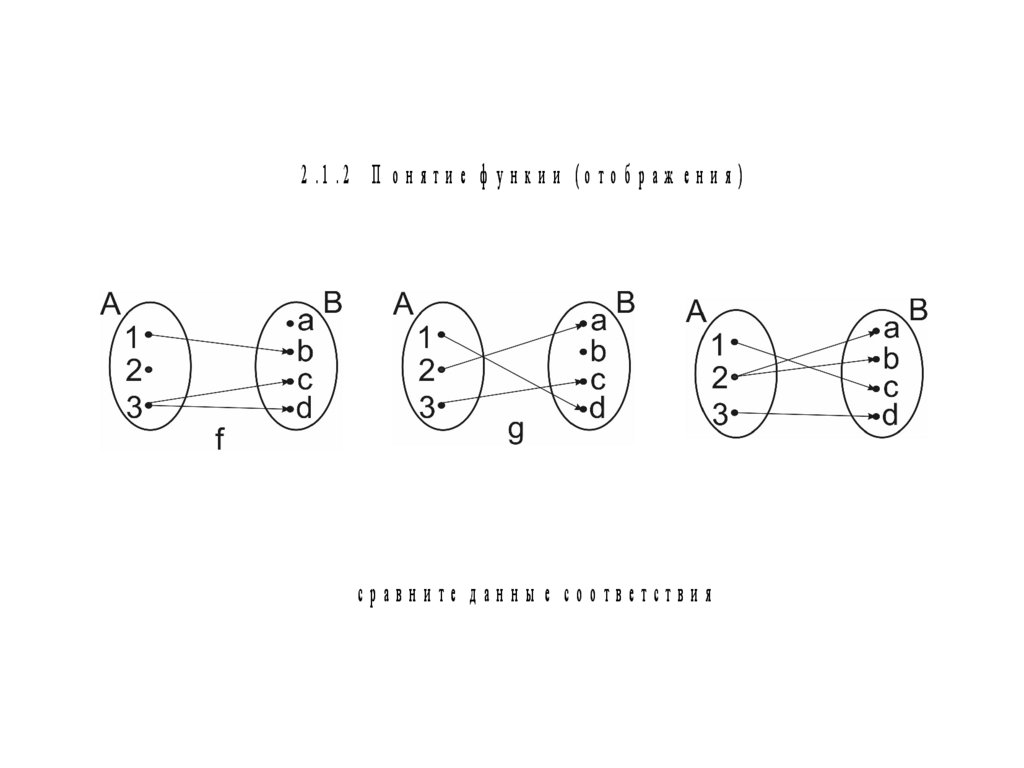
2 .1 .2 П о н я т и е ф у н к и и (о т о б р а ж е н и я )сравните данны е соответствия
47.
О пределение 1. С оответствие F , при которо м каж дом у элем ентум нож ества А соответствует единственны й эл ем ент м нож ества В ,
н азы вается ф ун кц и ей и ли отоб раж ен и ем , оп ред елен н ы м н а
м н ож естве А со зн ачен и ем в В .
О б озн ачен и е, F : A B , А - об ласть оп ред елен и я F .
48.
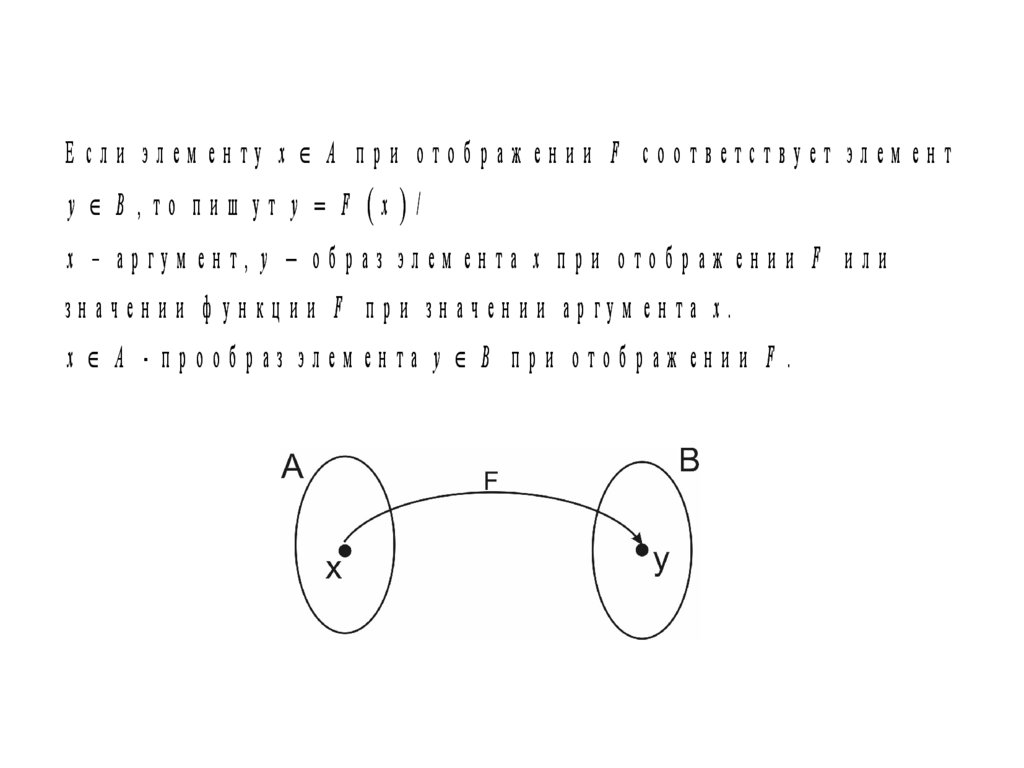
Е сли элем енту x A при отображ ении F соответствует элем ентy B , то пиш ут y F x /
x – аргум ен т, y образ элем ен та x п ри отображ ен и и F и ли
зн ачен и и ф ун кц и и F п ри зн ачен и и аргум ен та x.
x A - прообраз элем ента y B при отображ ении F .
49.
П рим еры .1) A N , В - м нож ество квадратов натуральны х чисел.
f :n n 2 является ли это соответствие отображ ением ?
50.
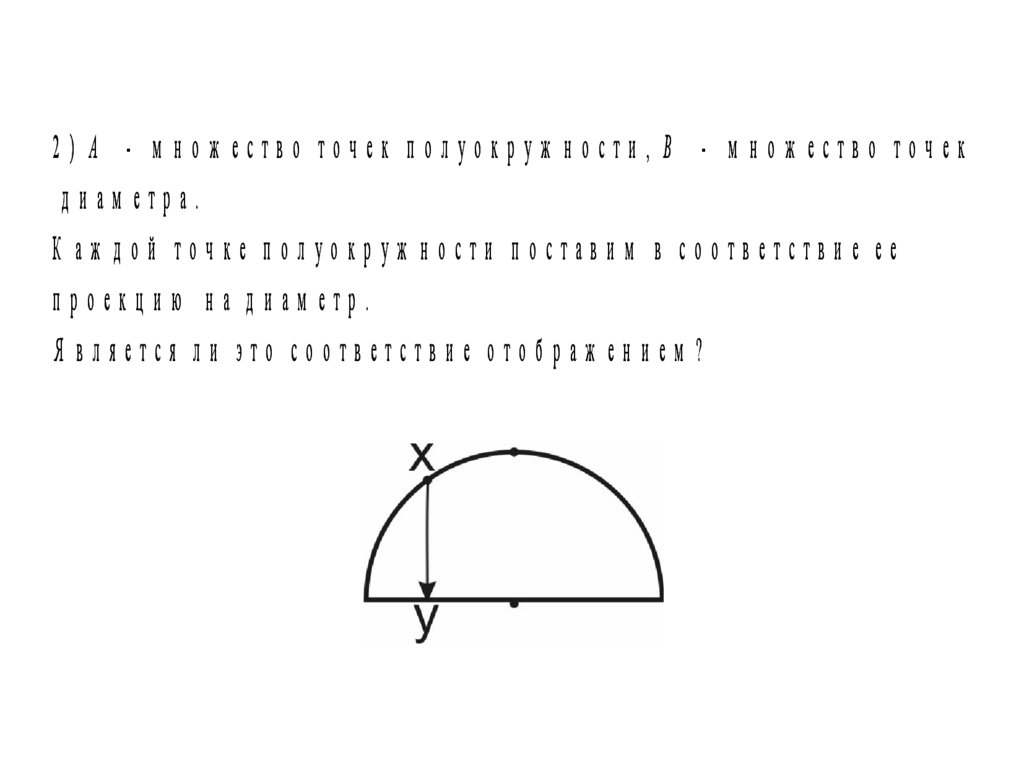
2) A - м нож ество точек полуокруж ности, B - м нож ество точекдиам етра.
К аж дой точке полуокруж ности поставим в соответствие ее
проекцию на диам етр.
Я вляется ли это соответствие отображ ением ?
51.
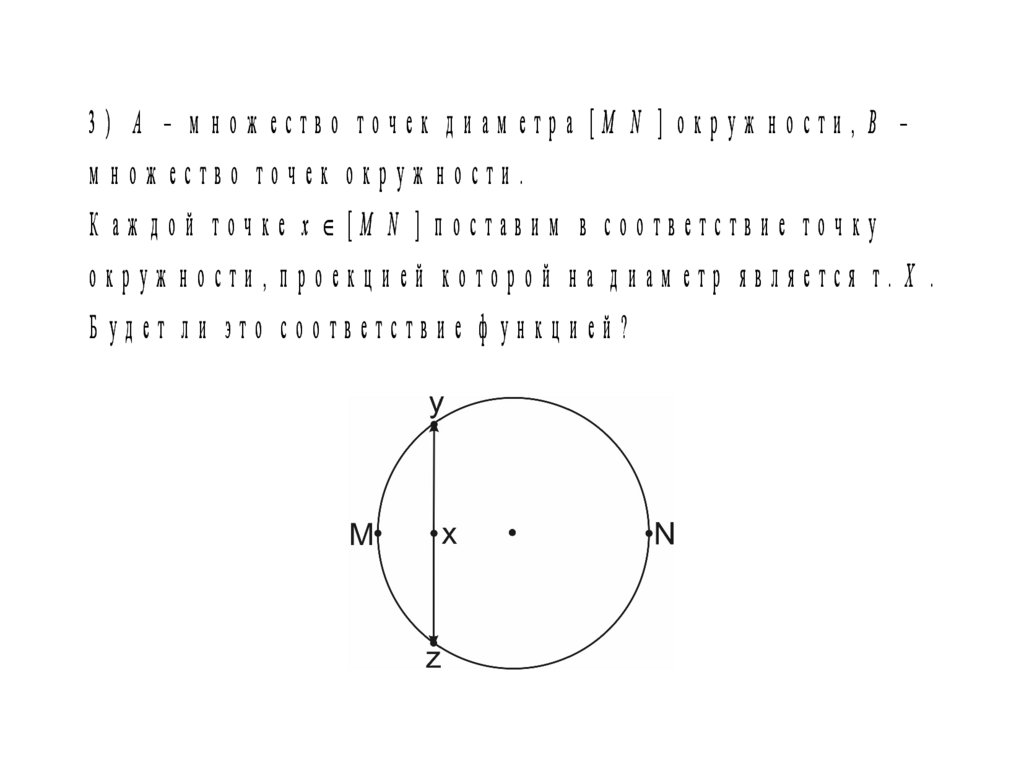
3) A – м нож ество точек диам етра [M N ] окруж ности, B –м нож ество точек окруж ности.
К аж дой точке x [M N ] поставим в соответствие точку
окруж ности, проекцией которой на диам етр является т. X .
Б удет ли это соответствие ф ункцией?
52.
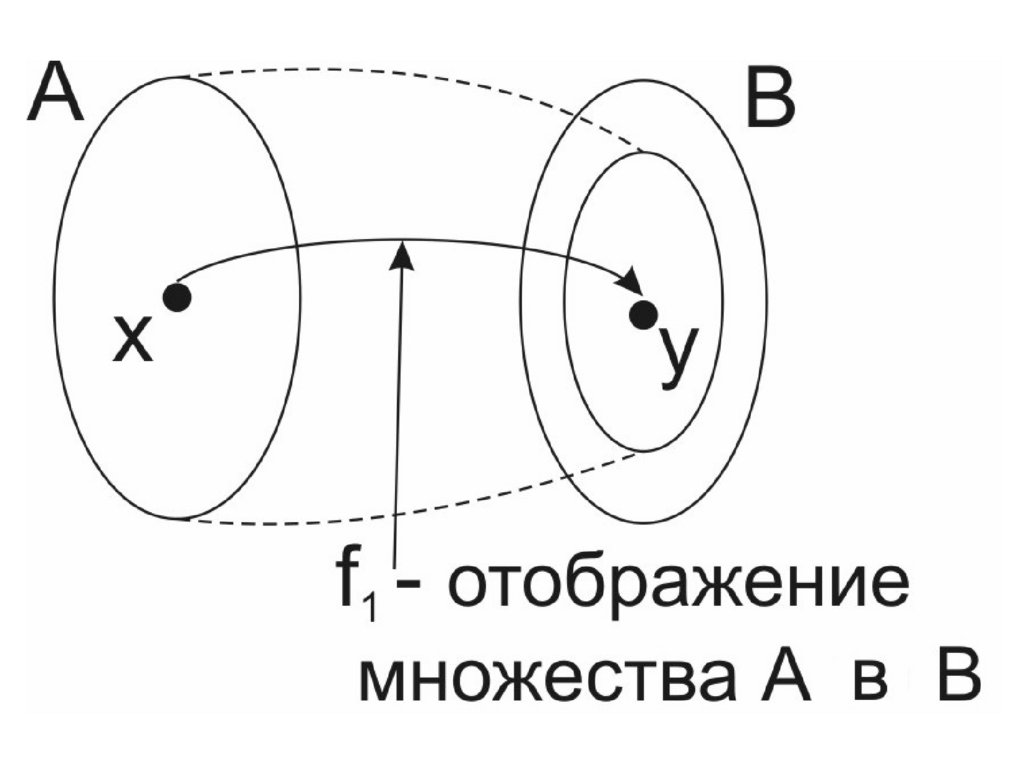
2 .2 В и д ы о т о б р а ж е н и йО п ред елен и е 1. О тоб раж ен и е F : A B н азы вается отоб раж ен и ем
м нож ества А в В , если в м нож естве В им еется хотя бы один
элем ен т, н е и м ею щ и й п рооб раза в м н ож естве А.
53.
54.
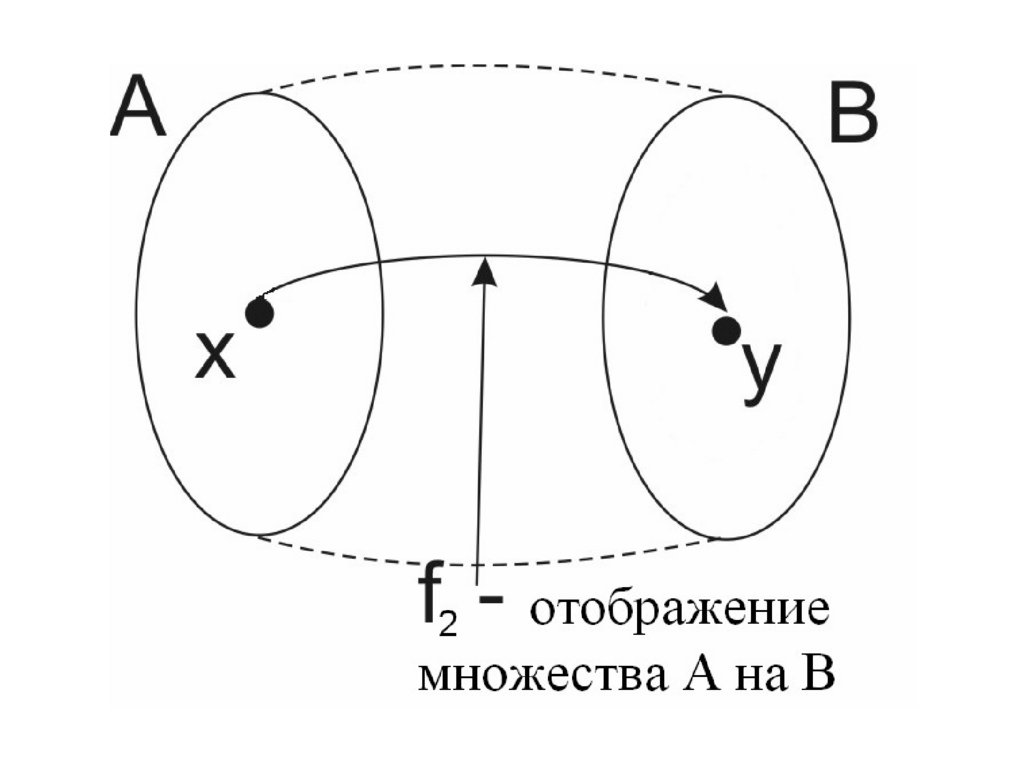
О п ред елен и е 2. О тоб раж ен и е F : A B н азы вается отоб раж ен и емм нож ества А на В , если каж ды й элем ент м нож ества В им еет
хотя бы один прообраз в м нож естве А.
55.
56.
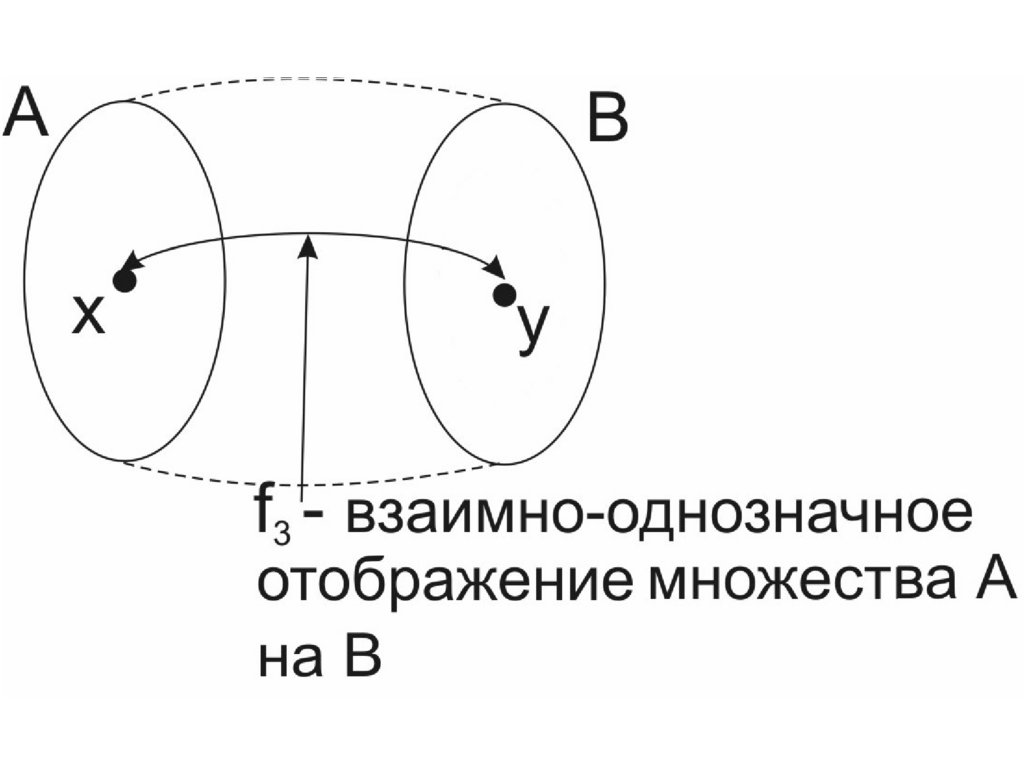
наО п ред елен и е 3. О тоб раж ен и е F : A B н азы вается взаи м н о
од н озн ачн ы м отоб раж ен и ем м н ож ества А н а В , если каж д ы й
элем ент м нож ества В им еет единственны й прообраз в
м нож естве А.
К ак м ож н о и н терп рети ровать н а кругах Э й лера?
57.
58.
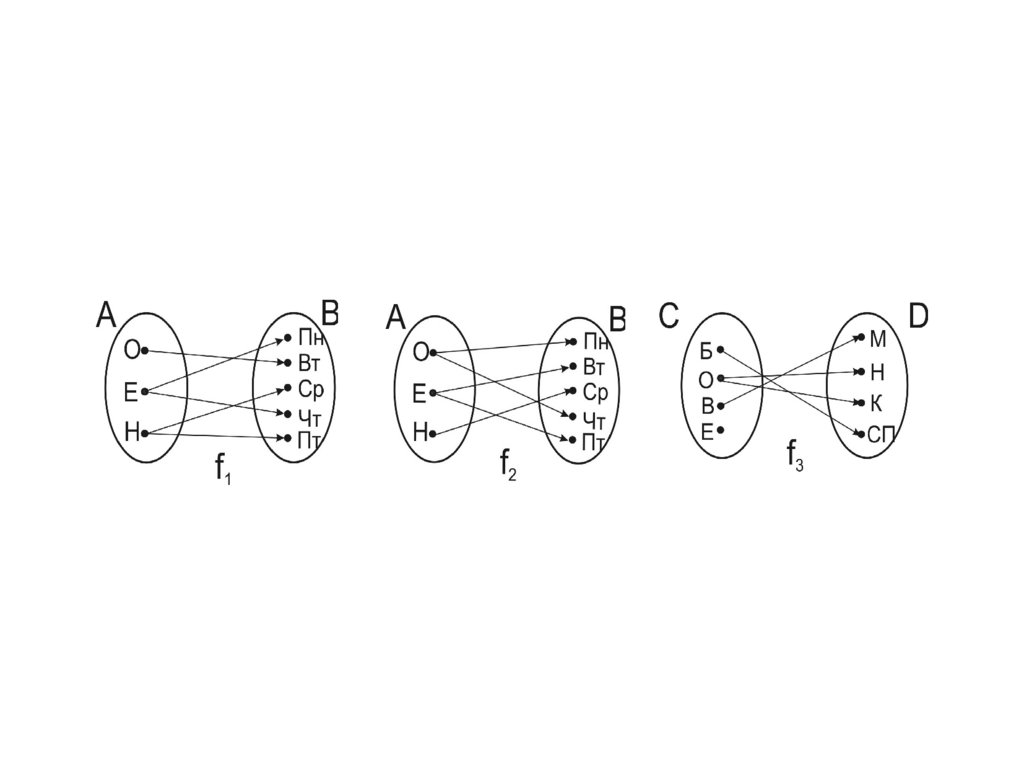
П рим еры .1 . A N , В - м н о ж е с т в о 2 N . f1 : n 2 n - о т о б р а ж е н и е А н а В .
2 . A R , B R , f2 : x x 2. f2 - о то б р аж ен и е А в В .
3 . A R , B R 0 , f 3 : x x 2 . f 3 - о т о б р а ж е н и е А н а В .
59.
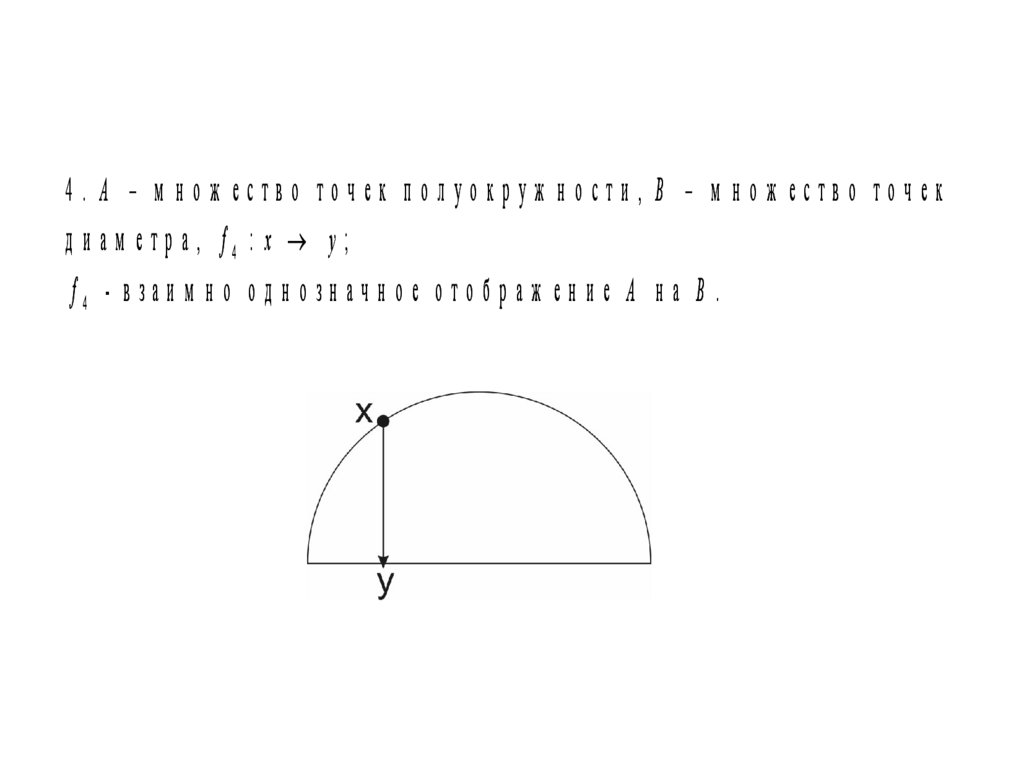
4. A – м нож ество точек полуокруж ности, B – м нож ество точекд и ам етр а, f4 : x y;
f4 - в заи м н о о д н о зн ач н о е о то б р аж ен и е A н а B .
60.
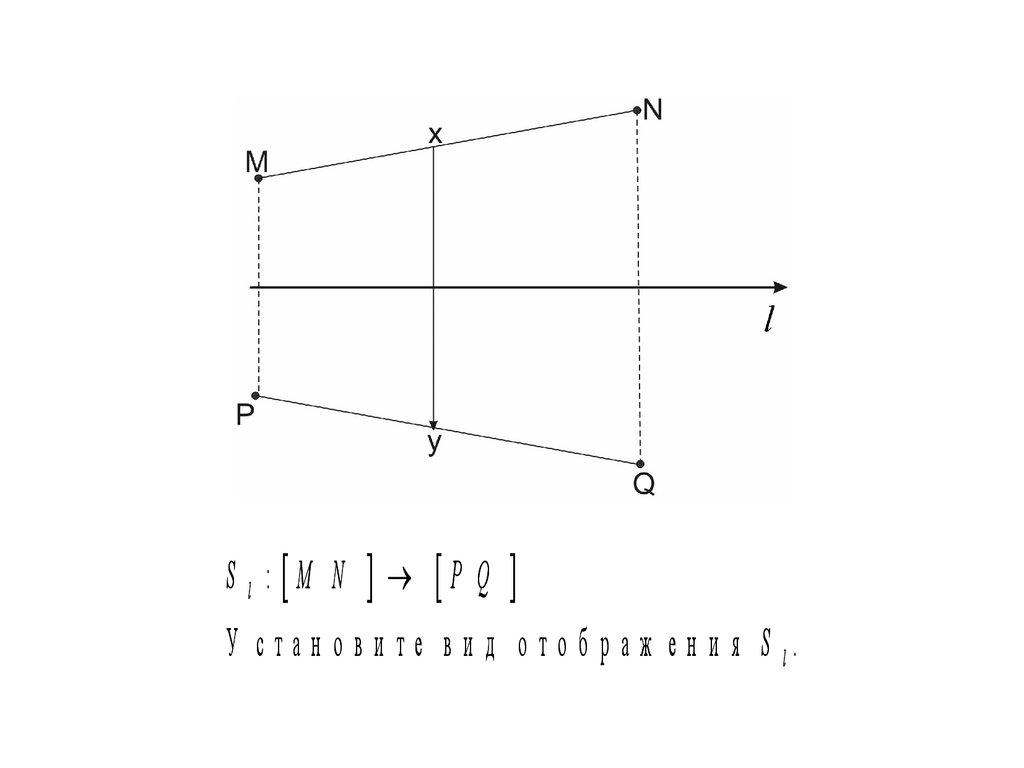
S l : M N P QУ с т а н о в и т е в и д о т о б р а ж е н и я S l.
61.
О п ред елен и е 4. О тоб раж ен и е f : A B н азы вается п остоян н ы м ,если сущ ествует такое b B , что для лю бого x A f x b.
П рим еры :
1) f x 5, D f R ;
2) x
x 1
, D R 1 .
x 1
62.
О п ред елен и е 5. О тоб раж ен и е f : A B , A R н азы ваетсято ж д ествен н ы м , есл и д л я л ю б о го x A , f x x.
О б о зн а ч а е т с я iA.
О пределение 6. П усть f : A B , D A. О тображ ение : D B
н а з ы в а е т с я с у ж е н и е м f н а D , е с л и д л я л ю б о г о x D x f x .
О б озн ачен и е
f D x .
63.
П рим еры .x 1, есл и x 1,
f x 2
x , если x 1.
f ,1 x x 1 , f 1 , x x 2 .
64.
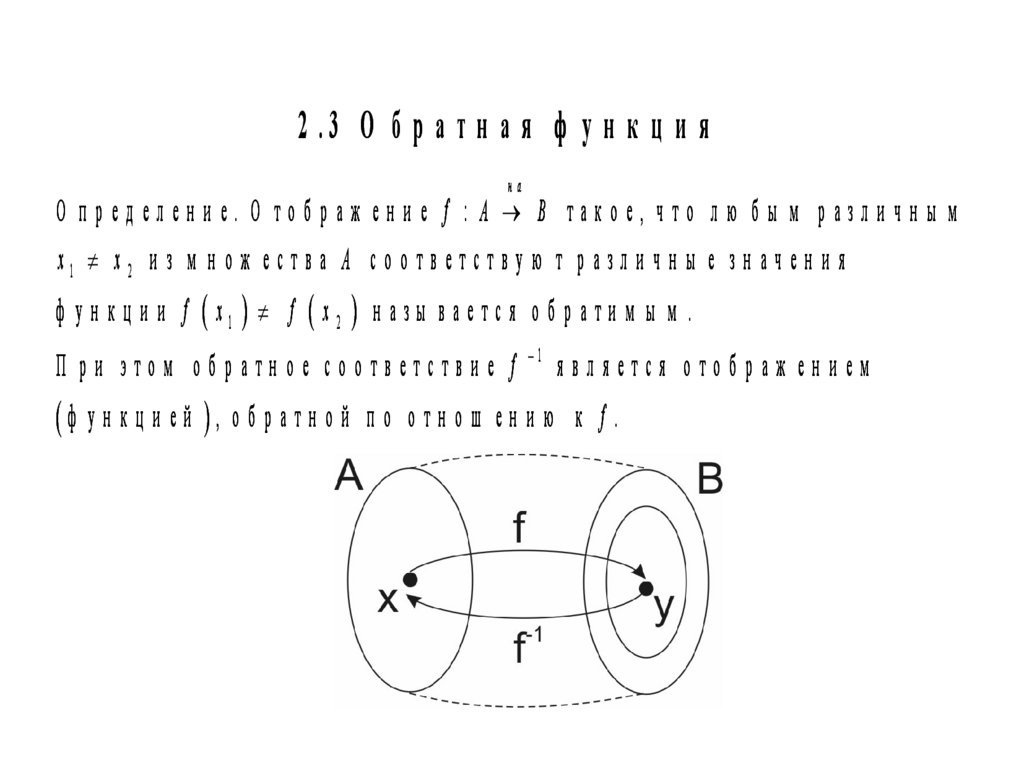
2 .3 О б р а т н а я ф у н к ц и яна
О п ред елен и е. О тоб раж ен и е f : A B такое, что лю б ы м разли чн ы м
x1 x 2 и з м н о ж е с т в а A с о о т в е т с т в у ю т р а зл и ч н ы е з н а ч е н и я
ф у н к ц и и f x1 f x 2 н а зы в а е т с я о б р а т и м ы м .
П р и э т о м о б р а т н о е с о о т в е т с т в и е f 1 я в л я е т с я о т о б р а ж е н и е м
ф у н к ц и е й , о б р а т н о й п о о т н о ш е н и ю к f .
65.
О б л а с т ь ю о п р е д е л е н и я о б р а т н о й ф у н к ц и и f 1 я в л я е т с ям н о ж е с т в о D f 1 B , а м н о ж е с т в о м з н а ч е н и й м н о ж е с т в о А область определения ф ункции f .
П рим еры .
1. y 3x 4, D R , E R
y 4
x
- обратная ф ункция.
3
66.
2 . y 2 x , D R , E 0 , .О б р а т н о й д л я д а н н о й ф у н к ц и и я в л я е т с я ф у н к ц и я x lo g 2 y ,
D 1 0 , , E 1 R .
3 . y x 2 , D R , E 0 , . Э т а ф у н к ц и я н е о б р а т и м а , т .к .
разли чн ы м зн ачен и ям аргум ен та x и x соответствует од н о
зн ач ен и е ф ун к ц и и x x .
2
2
67.
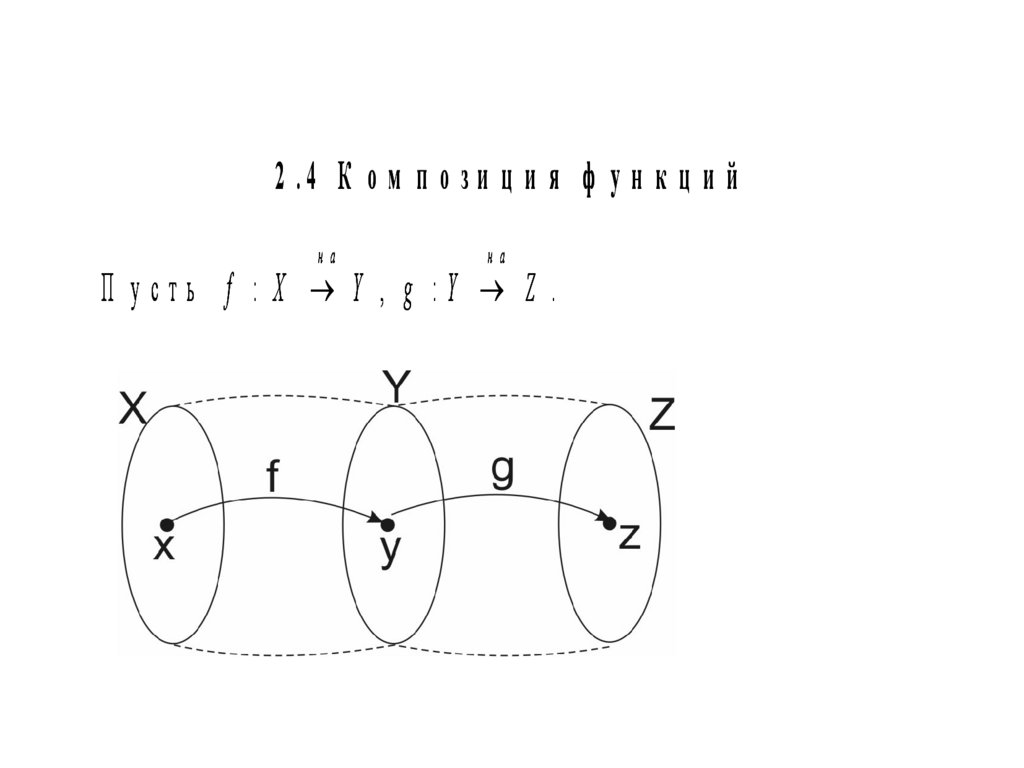
2 .4 К о м п о з и ц и я ф у н к ц и йна
на
П усть f : X Y , g :Y Z .
68.
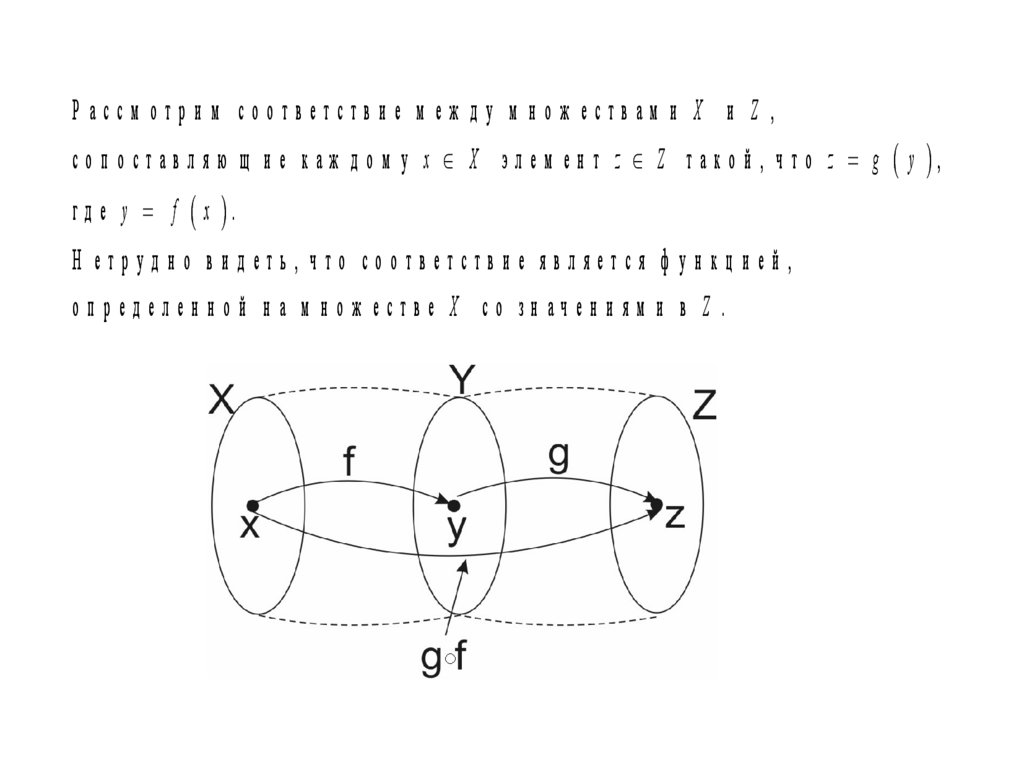
Р ассм отрим соответствие м еж ду м нож ествам и X и Z ,с о п о с т а в л я ю щ и е к а ж д о м у x X эл е м е н т z Z т а к о й , ч т о z g y ,
г д е y f x .
Н етрудно видеть, что соответствие является ф ункцией,
оп ред елен н ой н а м н ож естве X со зн ачен и ям и в Z .
69.
Т акая ф ун кц и я н азы вается ком п ози ц и ей ф ун кц и й f и g .О б о зн а ч а е т с я g f x z g y g f x и л и
g f x g f x
f - внутренняя ф ункция, g - внеш няя ф ункция.
70.
О п ред елен и е. К ом п ози ц и ей ф ун кц и й f и g н азы вается ф ун кц и я,определяем ая равенством
g f x g f x д л я в с е х x , д л я
которы х правая часть им еет см ы сл.
71.
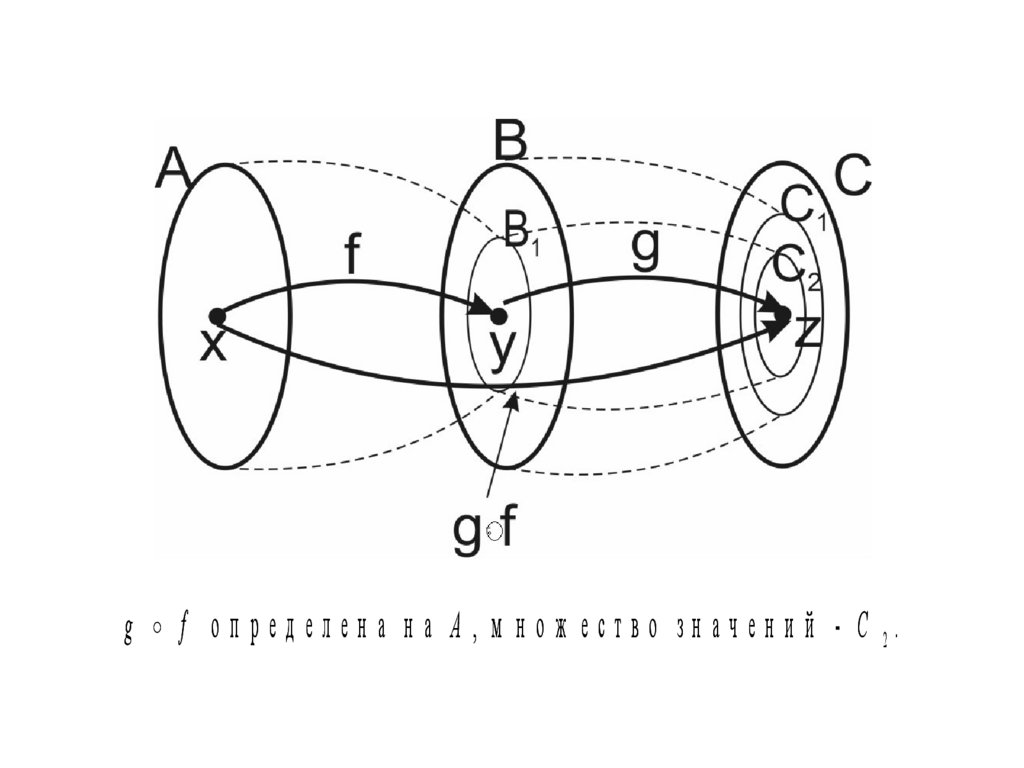
g f о п р ед ел ен а н а А , м н о ж еств о зн ач ен и й - C 2.72.
П рим ерыy x 2 , D 1 R , E 1 0 ;
1)
E2 D2
z 3 y 5 , D 2 R , E 2 R
Зн ачи т д ве ф ун кц и и f , g об разую т слож н ую ф ун кц и ю
2
и
л
и
к
о
м
п
о
з
и
ц
и
ю
z
3
x
5, D 3 R.
73.
y tg x , D 1 0 , , E 1 0 ,14
2)
E D 2
z 1 y , D 2 ,1
Э ти ф ун кц и и об разую т слож н ую ф ун кц и ю
z
1 tg x , D 3 0 , .
4
74.
y s in x , D 1 0 ; 2 , E 1 1 ,13)
E1 D
z l g y , D 2 0 ; , E 2 ;
п о э т о м у с л о ж н а я ф у н к ц и я z lg s in x с у щ е с т в у е т л и ш ь д л я т е х х ,
д л я к о т о р ы х s in x 0 ,1 , т .е . н а D 1 = 0 , 0 , 2 .
И т а к , z lg s in x , D 3 0 , .
75.
y 2 s i n x 3 , D 1 R , E 1 5 , 14)
E1 D 2 .
z y , D 2 0 ; , E 2 0 ,
Зн ачи т эти д ве ф ун кц и и н е об разую т слож н ую ф ун кц и ю .























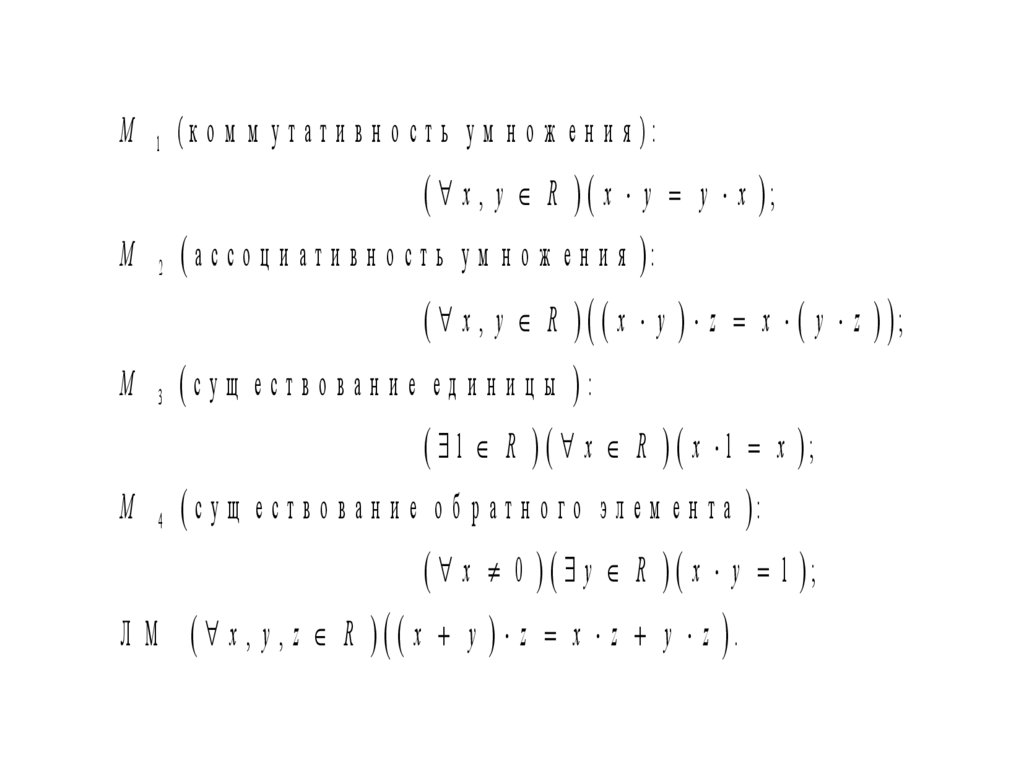


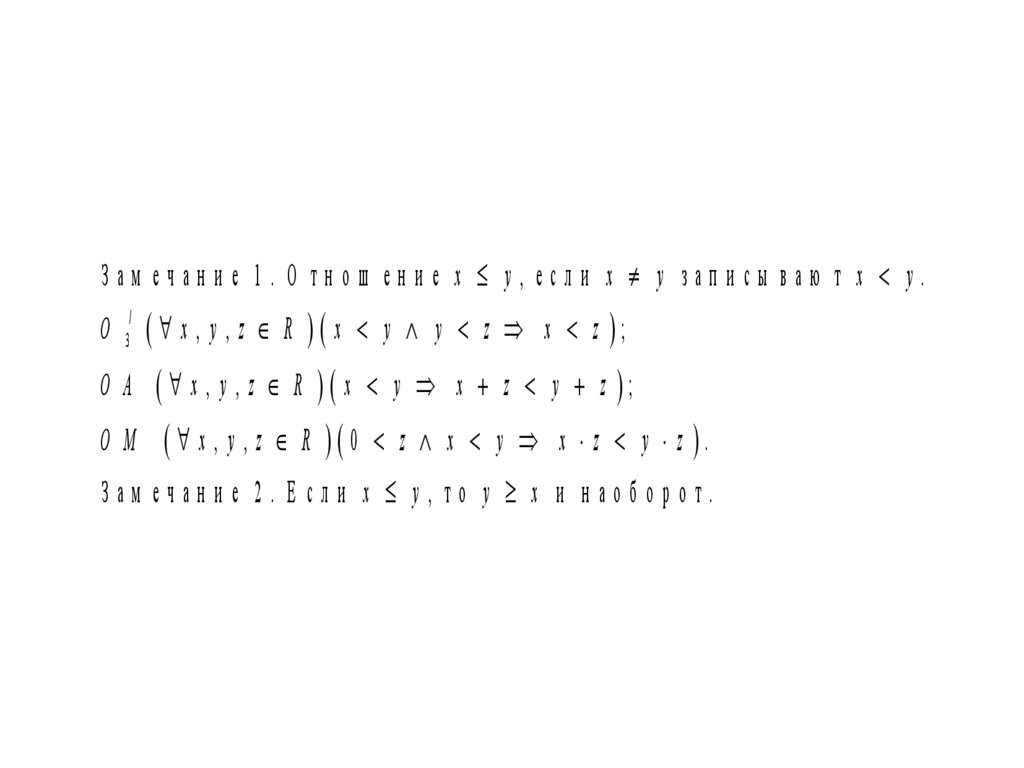






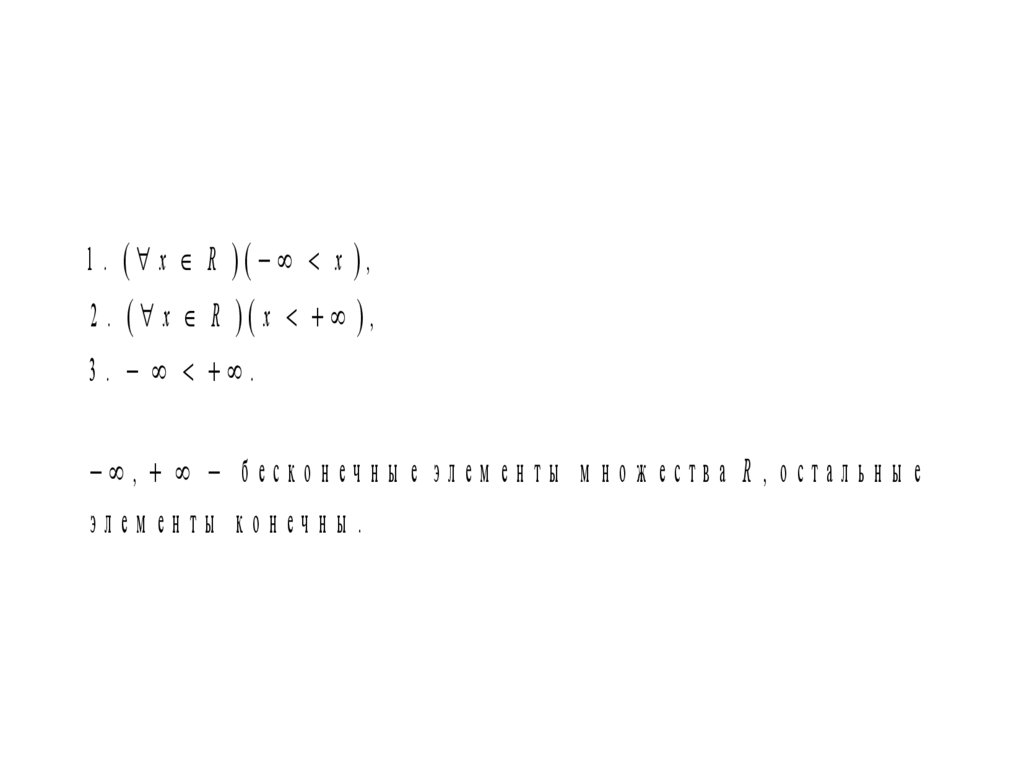




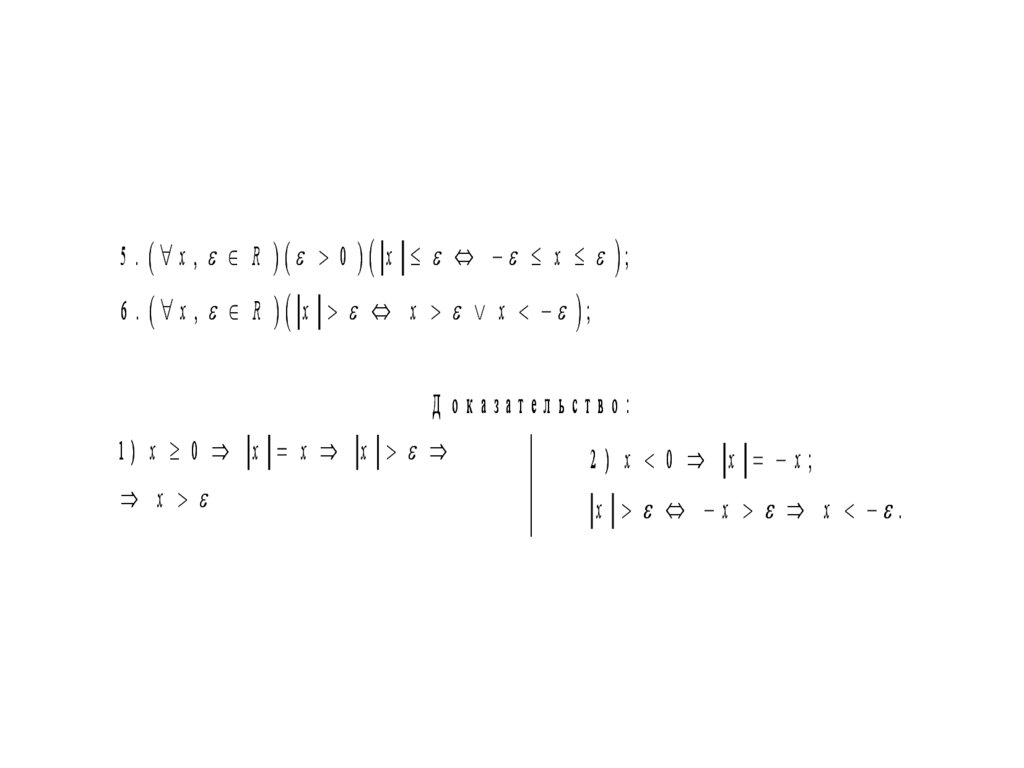
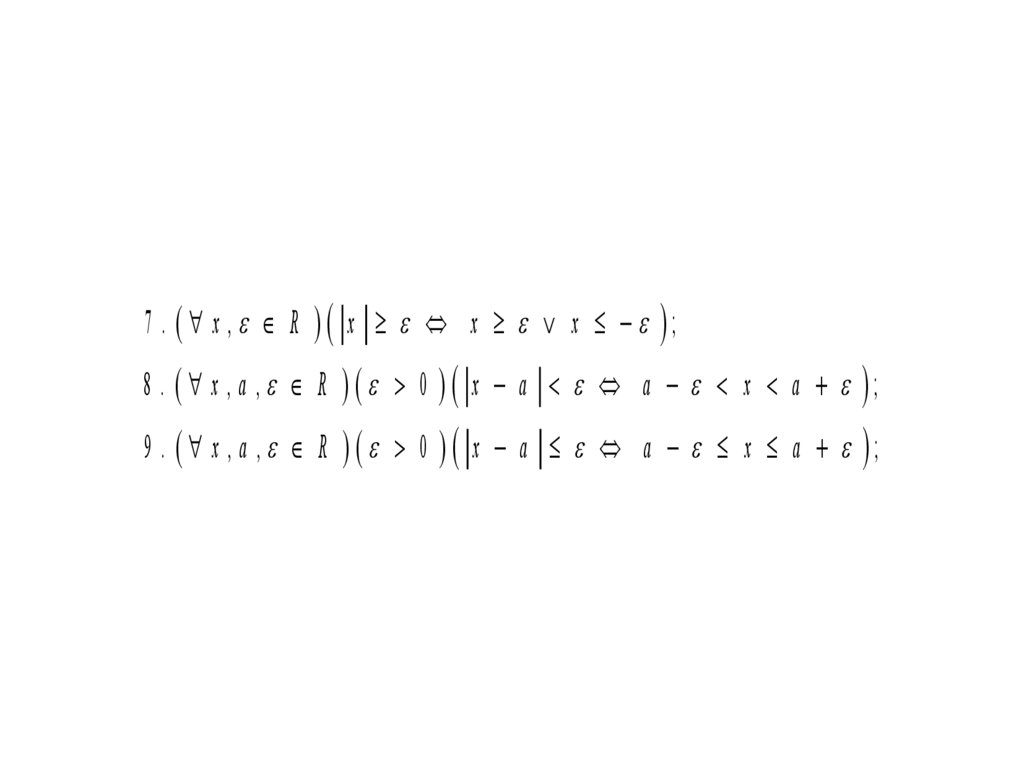










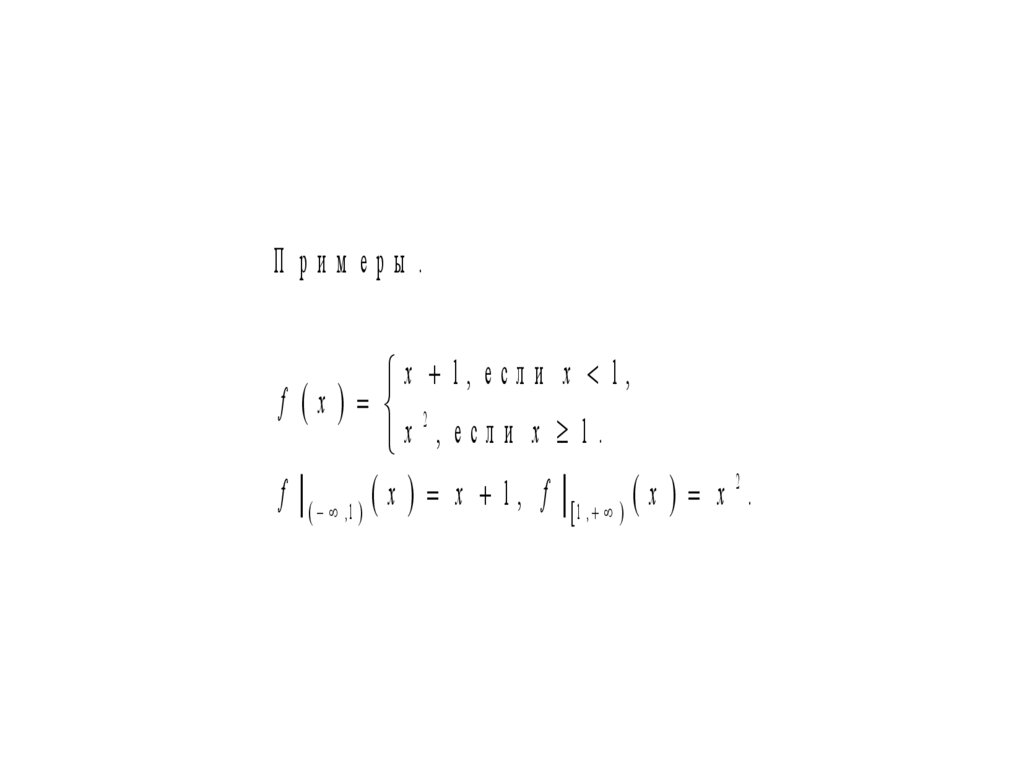




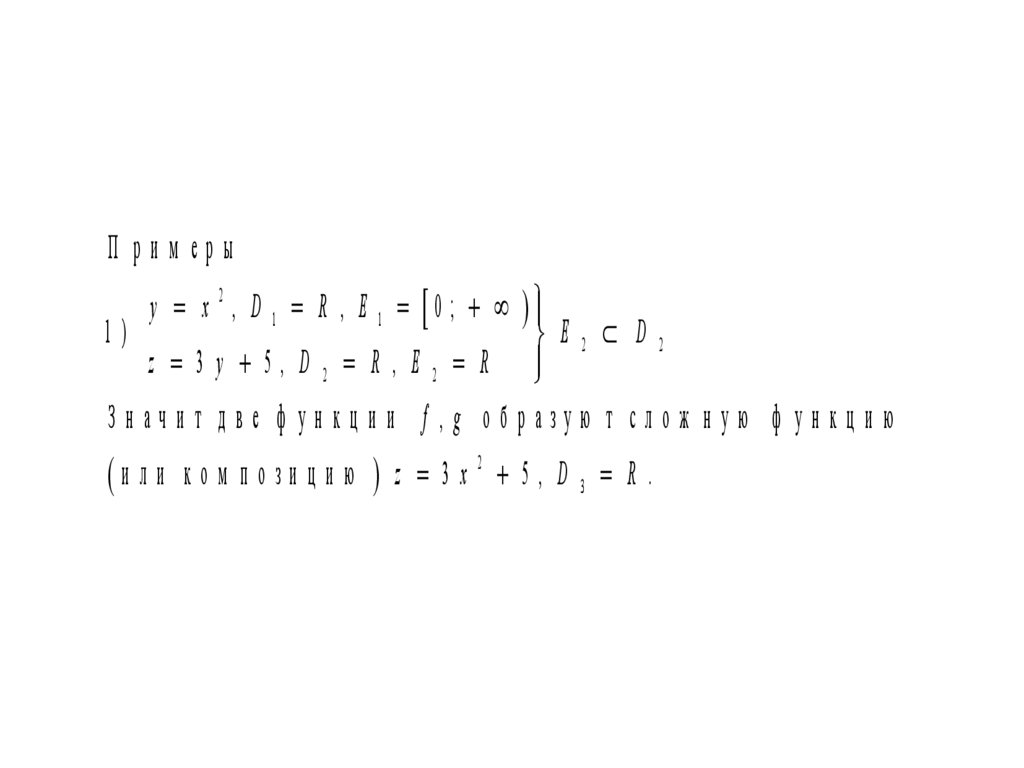
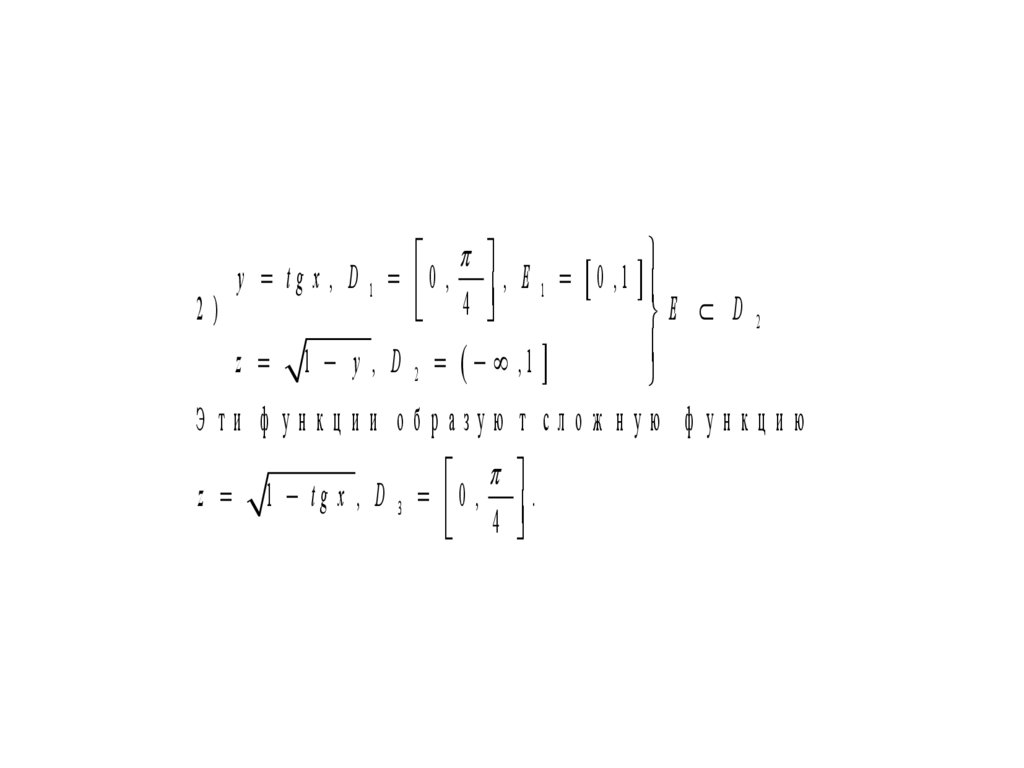
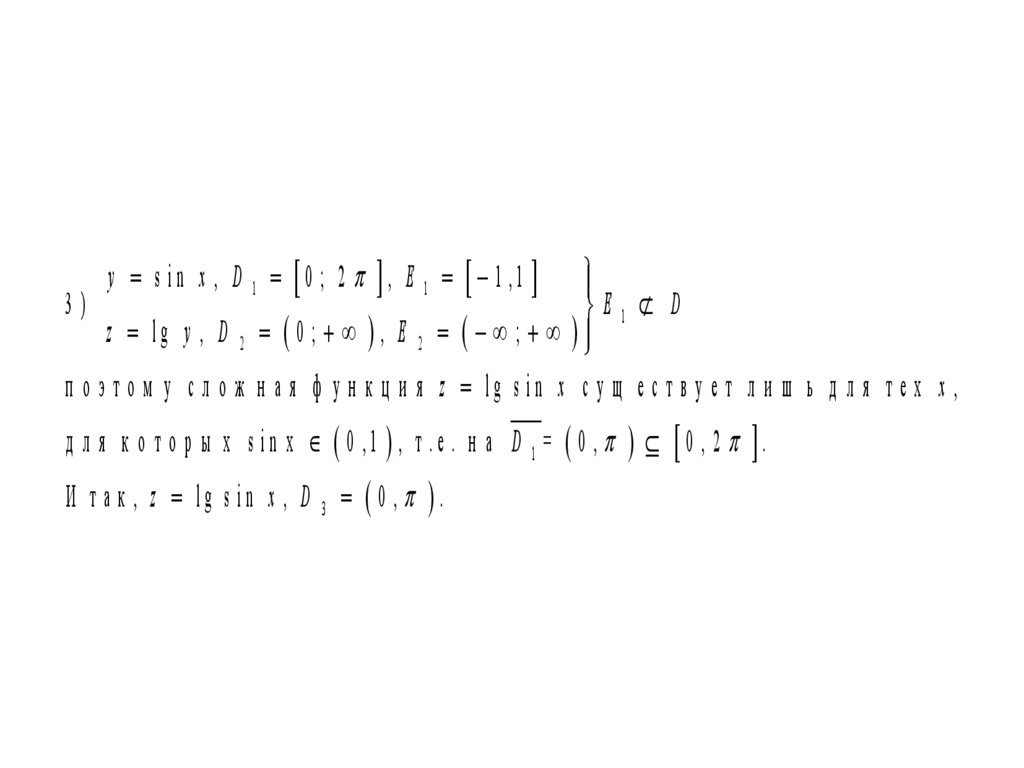
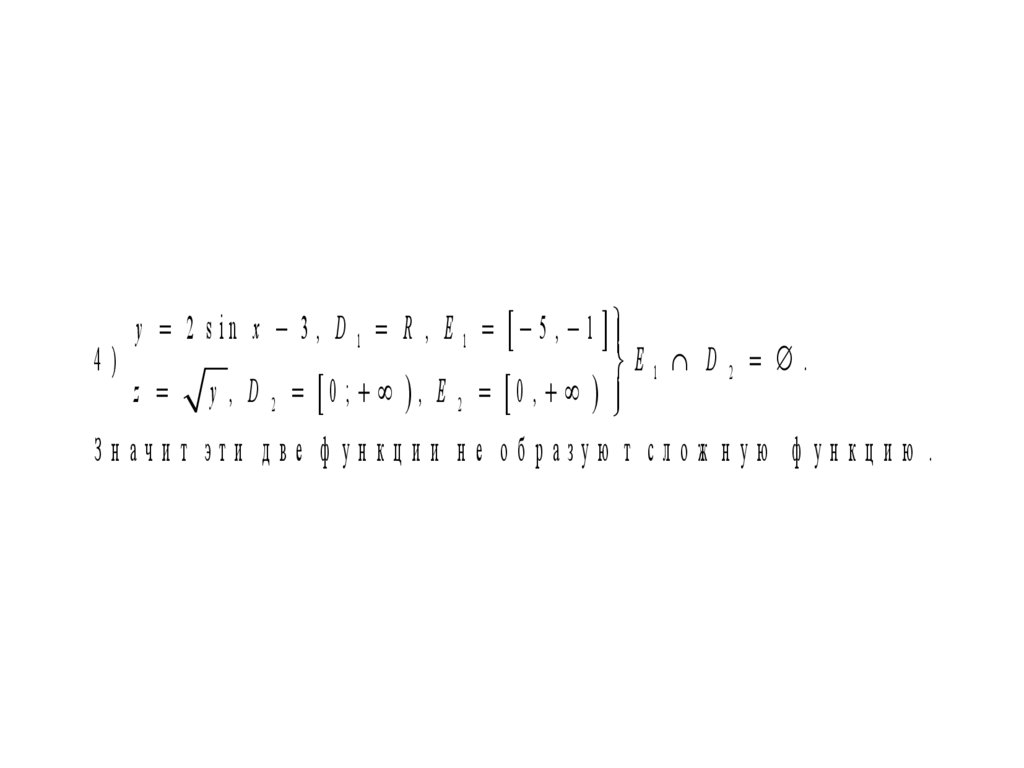

 Информатика
Информатика








