3сем_Лк 3_Ду высш поряд

1.

Первое высшее техническое учебное заведение России
Санкт-Петербургский горный университет императрицы Екатерины II
Кафедра высшей математики
Лекция 3. ДУ высшего порядка, допускающие
понижение порядка
22.12.2025
г. Санкт-Петербург
2025
1|11

2.

ДУ n-го порядка
y
(n)
f ( x)˜ (1
f(x) непрерывна в интервале (а, b)
)
z(x) y ( n 1) ( x)
Метод интегрирования: замена
ДУ 1-го порядка с разделенными переменными
d
z ( x) f ( x)
dx
d
y ( x)
z ( x)
dx
(n)
z ( x)
f ( x)dx С1
приводит к
dz f ( x)dx.
или
y
( n 1)
( x)
f ( x)dx С
Последовательно интегрируем n раз, понижая степень производной.
Будут появляться n произволных постоянных
Общее решение ДУ (1) всегда существует; особых решений нет.
2|11
1

3.

Пример 1. Найти частное решение ДУ y 1 x ( x 0)
удовлетворяющее начальным условиям: y (1) 1
y (1) 3
Понизим порядок ДУ:
z ( x) y ( x)
y ( x) ln x C1
z 1/ x
y ( x) ln xdx C1 x C2
Общее решение ДУ:
y (1) 1
1 1 C1 C 2
y x ln x x C1 x C 2
C 2 1
C1 C 2 2
y (1) 3
3 ln 1 C1
z ( x) ln x C1
Решение задачи Коши:
y ( x) x ln x 2 x 1.
C1 3
3|11

4.

Общее решение ДУ y cos x имеет вид:
?
?
1) y sin x C1 x C 2
2) y sin x C1 x C 2
3) y cos x C1 x C 2
4) y cos x C1 x C 2
y cos x , удовлетворяющее
начальным условиям:
y (0) 1
y (0) 1
Частное решение ДУ
1) y cos x 2 x 2
2) y cos x х 2
3) y cos x x 2
4) y cos x 2
4|11

5.

:
ДУ 2-го порядка, допускающие понижение порядка
Случай 1: ДУ не содержит
искомой функции y(x):
F x, y ( x), y ( x) 0
(2)
Введем новую переменную z (x) :
ДУ 1-го порядка F x, z ( x), z ( x) 0
y ( x) z ( x)
Общее решение (3) : z ( x ) f ( x, C1 )
ДУ с разделяющимися переменными:
Общее решение (2) :
y ( x) f ( x,C1 )dx C2 .
5|11
y ( x) f ( x,C1 )
(3)

6.

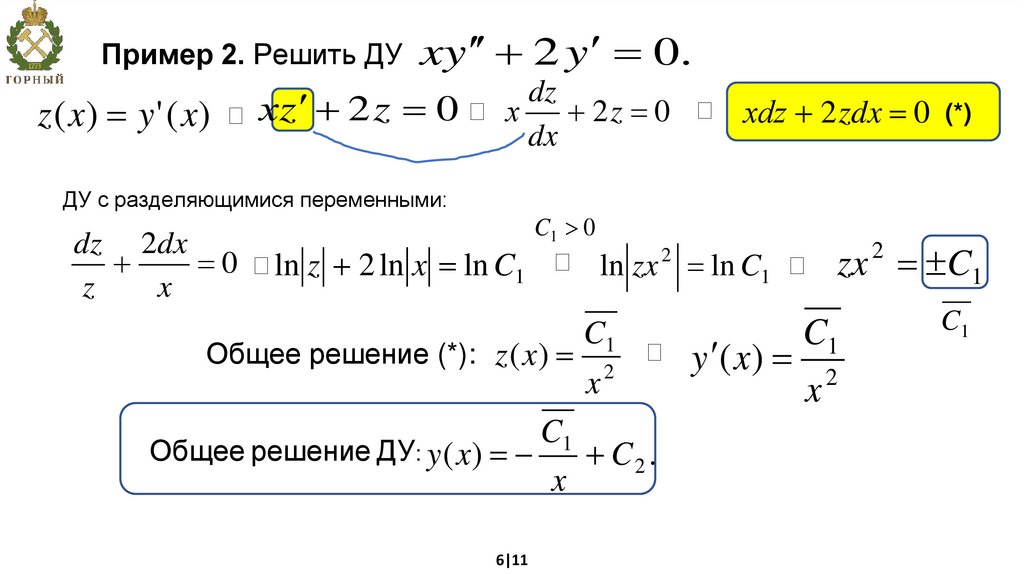
Пример 2. Решить ДУ xy 2 y 0.
z ( x) y ' ( x)
хz 2 z 0
dz
х
2z 0
dx
ДУ с разделяющимися переменными:
dz 2dx
0
z
x
ln z 2 ln x ln C1
C1 0
Общее решение (*): z ( x)
zx C1
2
ln zx ln C1
2
C1
x
2
C1
Общее решение ДУ: y ( x)
C2 .
x
6|11
хdz 2 zdx 0 (*)
y ( x)
C1
x
2
C1

7.

?
Найти частное решение ДУ xy 2 y 0,
удовлетворяющее условиям: y (1) = 2 , y’ (1) = 1
C1
C2 .
Общее решение ДУ: y ( x)
x
C2 3
C1 C 2 2
y (1) = 2
y’ (1) = 1
y ( x)
C1
x
2
1
y ( x) 3
x
C1 1
7|11

8.

F y ( x ), y ( x ), y ( x ) 0. (4)
Случай 2: ДУ не содержит
независимую переменную х:
y ( x) z ( y )
dz dy
d
z( y) z ( y)
y ( x)
z( y)
dy dx
dx
F y, z ( y ), z ( y ) z ( y ) 0.
(5)
Общее решение ДУ (5):z ( y ) f ( y ,C1 )
y ( x) f ( y,C1 )
ДУ с разделяющимися
переменными
dу
dx
dy
Общий интеграл ДУ (4) :
x C2 .
f ( y,C1 )
8|11
dy
dx 0
f ( y,C1 )

9.

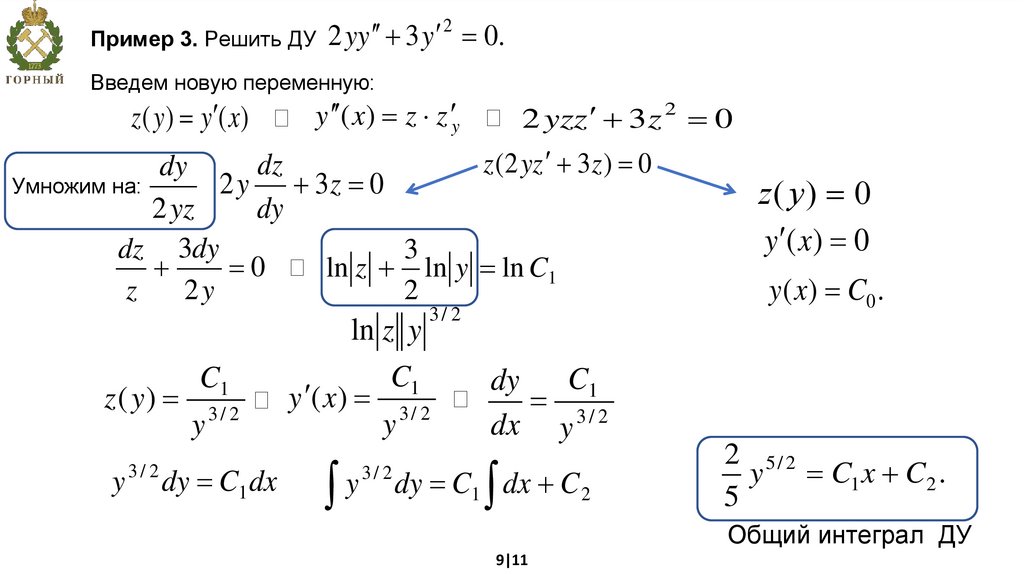
2
Пример 3. Решить ДУ 2 yy 3 y 0.
Введем новую переменную:
z ( y ) y ( x)
y ( x) z z y
2 yzz 3 z 2 0
z (2 yz 3z ) 0
dz
dy
Умножим на:
2 y 3z 0
dy
2 yz
dz 3dy
3
0
ln z ln y ln C1
2
z
2y
3/ 2
ln z y
z( y)
C1
y
3/ 2
y 3 / 2 dy C1 dx
y ( x)
y
C1
y
3/ 2
3/ 2
C1
dy
3/ 2
dx y
dy C1 dx C 2
z( y) 0
y ( x) 0
y ( x) C0 .
2 5/ 2
y C1 x C2 .
5
Общий интеграл ДУ
9|11

10.

Правда ли, что…
1. Понизить порядок ДУ
можно заменой
y ( x) z ( y )
2. Понизить порядок ДУ
можно заменой
y ( x) z ( х)
3. Общее решение ДУ y 24 х имеет вид:
10|11
y х C
4

11.

Спасибо за внимание
Кафедра высшей математики;
Санкт-Петербургский горный
университет императрицы
Екатерины II;
199106, Санкт-Петербург,
Васильевский остров, 21 линия д.2;
Тел.: +7(812) 328-82-31;
E-mail: kafmatem@spmi.ru
11|11