ДУ_3 (1)

1.

Глава 2. «ДИФФЕРЕНЦИАЛЬНЫЕ
УРАВНЕНИЯ ВТОРОГО И ВЫСШИХ
ПОРЯДКОВ»
ПЛАН
1. ОБЩИЕ СВЕДЕНИЯ О
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЯХ 2 порядка
2. НЕПОЛНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ
УРАВНЕНИЯ 2 порядка

2.

П.1. Общие сведения о
дифференциальных уравнениях 2
порядка
ОПРЕДЕЛЕНИЕ 1.1
Дифференциальным уравнением 2 порядка,
разрешенным относительно второй
производной, называют уравнение вида
y f ( x; y; y )

3.

Решением этого уравнения называют такую
функцию, которая дважды дифференцируема на
некотором интервале и обращает данное
уравнение в тождество на этом интервале.
Задача Коши здесь ставит
своей
целью
нахождение
такого решения уравнения,
которое удовлетворяло бы
заданным
начальным
условиям
y
y
y
y0
0
x x
x x0
0
Для дифференциальных
уравнений 2 порядка
справедлива теорема
существования и
единственности решения
задачи Коши

4.

Общее решение дифференциального уравнения 2
порядка есть семейство функций у = φ(х:С1;С2),
зависящее от двух произвольных постоянных С1; и С2,
такое, что при любых значениях С1 и С2 функция
у = φ(х;С1,С2) есть решение данного уравнения и для
любых начальных условий
y
yи
x x0
0
y
x x0
y0
найдутся числа Ĉ1 и Ĉ2 , с которыми функция
у = φ(х, Ĉ1 ; Ĉ2 ) является решением задачи Коши
исходного уравнения.

5.

Общий интеграл уравнения
у" = f(х;у;у') представляет собой
соотношение
Ф(х;у;С1;С2)=0,
задаваемое
общее
решение
уравнения неявным образом.

6.

П.2. НЕПОЛНЫЕ
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
2 ПОРЯДКА
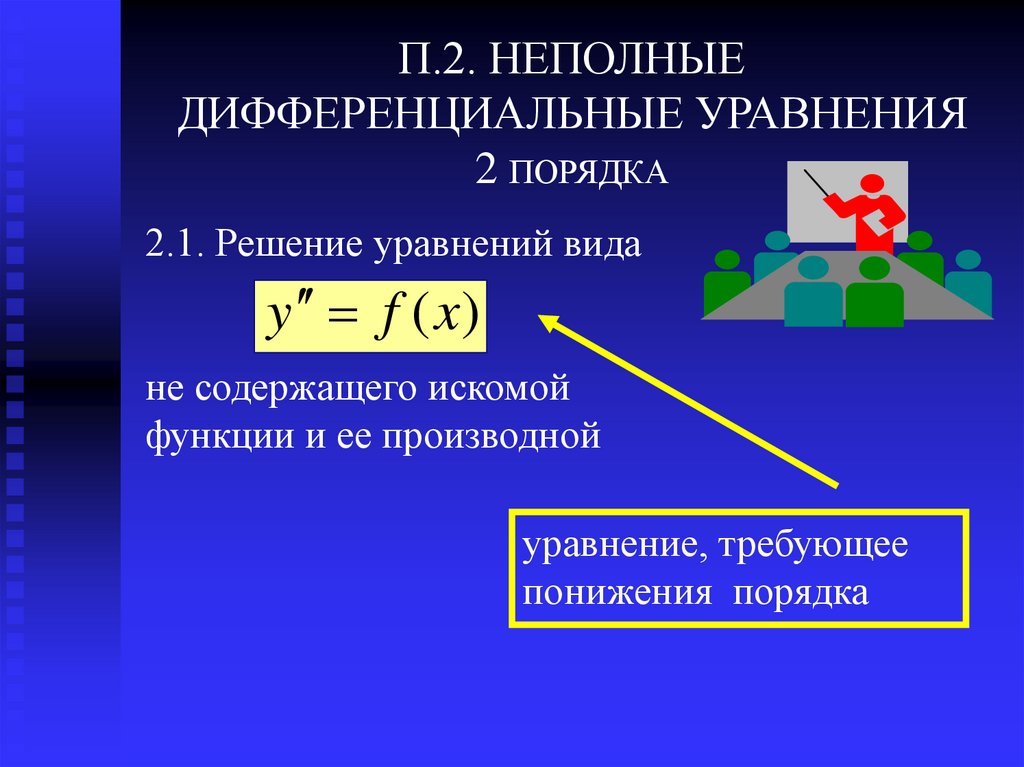
2.1. Решение уравнений вида
y f (x)
не содержащего искомой
функции и ее производной
уравнение, требующее
понижения порядка

7.

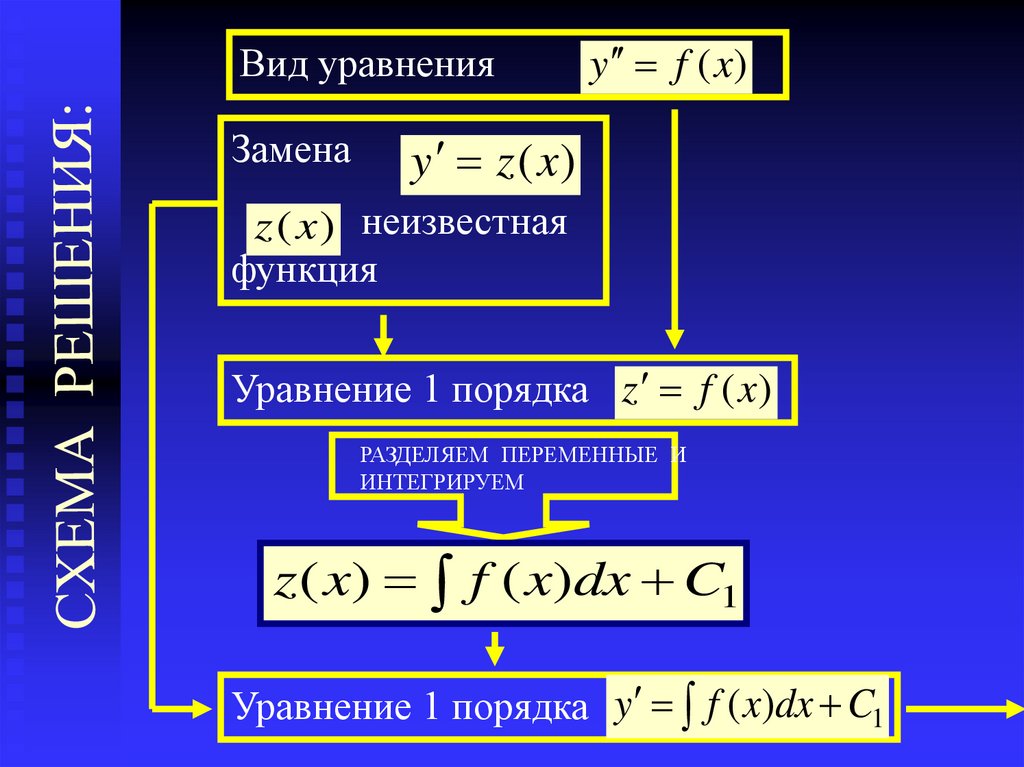
Вид уравнения
Замена
y f (x)
y z (x )
z (x ) неизвестная
функция
Уравнение 1 порядка z f (x)
РАЗДЕЛЯЕМ ПЕРЕМЕННЫЕ И
ИНТЕГРИРУЕМ
z ( x) f ( x)dx C1
Уравнение 1 порядка y f ( x)dx C1

8.

Интегрируем второй раз
Общее решение
y f ( x)dx dx C1 x C2
C1 и C2- const
Примером такого решения
является уравнение
y x

9.

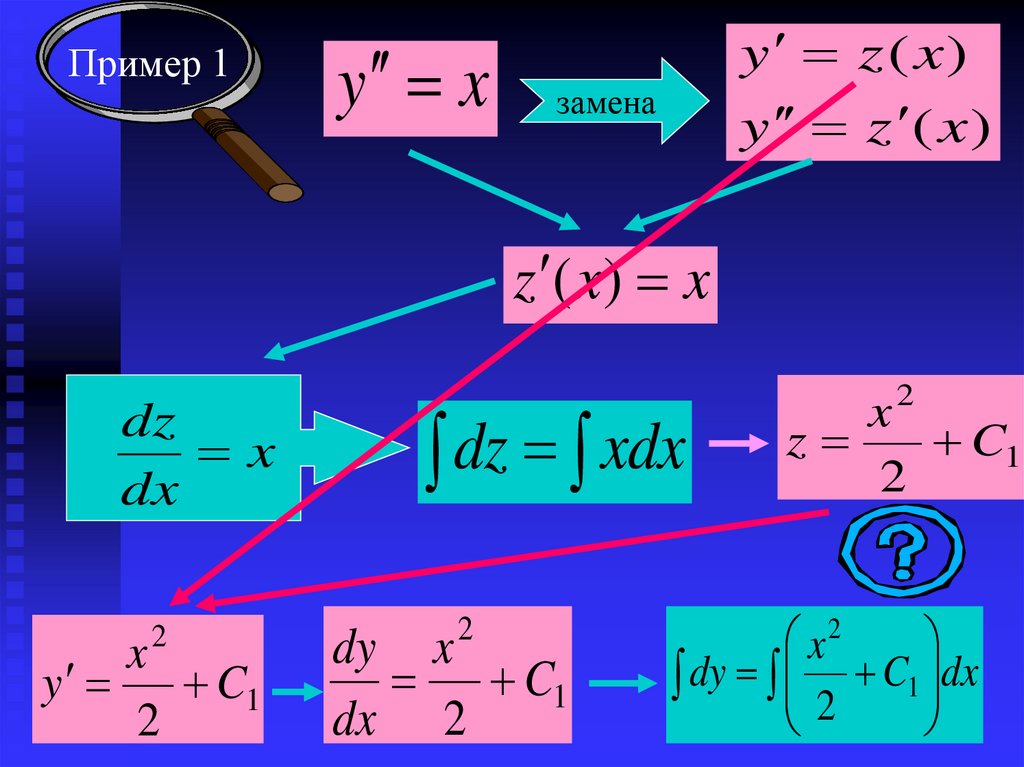
Пример 1
y x
y z ( x)
y z ( x )
замена
z ( x) x
dz
x
dx
2
x
y
C1
2
dz xdx
2
dy x
C1
dx 2
x2
z
C1
2
x2
dy 2 C1 dx

10.

3
x
y C1 x C 2
6
ОБЩЕЕ РЕШЕНИЕ НЕПОЛНОГО
ДИФ. УР. 2 ПОРЯДКА
!

11.

РЕШЕНИЕ НЕПОЛНОГО ДИФФЕРЕНЦИАЛЬНОГО
УРАВНЕНИЯ, ТРЕБУЮЩЕГО ПОНИЖЕНИЯ ПОРЯДКА
y 2 sin x 0
ПРИМЕР 2.
понизим порядок производной заменой
z ( x) 2 sin x 0
y z ( x)
y z ( x)
dz
2 sin x
dx
z 2 cos x C1
dy ( 2 cos x C1 )dx
y 2 cos x C1
dz 2 sin xdx
dy
2 cos x C1
dx
y 2 sin x C1 x C2

12.

2.2.Решение уравнений вида y f ( x; y )
РЕШЕНИЯ:
не содержащего искомой функции
Вид уравнения y f ( x; y )
Замена
y z (x )
z (x ) Неизвестная функция
СХЕМА
Уравнение 1 порядка
Общее промежуточное
решение z ( x; C1 )
z f ( x; z )
Методы
решения ДУ/
Уравнение 1 порядка y ( x; C1 )

13.

y ( x; C1 )dx C 2
C1 и C2- const
Общее решение неполного ДУ второго
порядка, требующего понижения порядка

14.

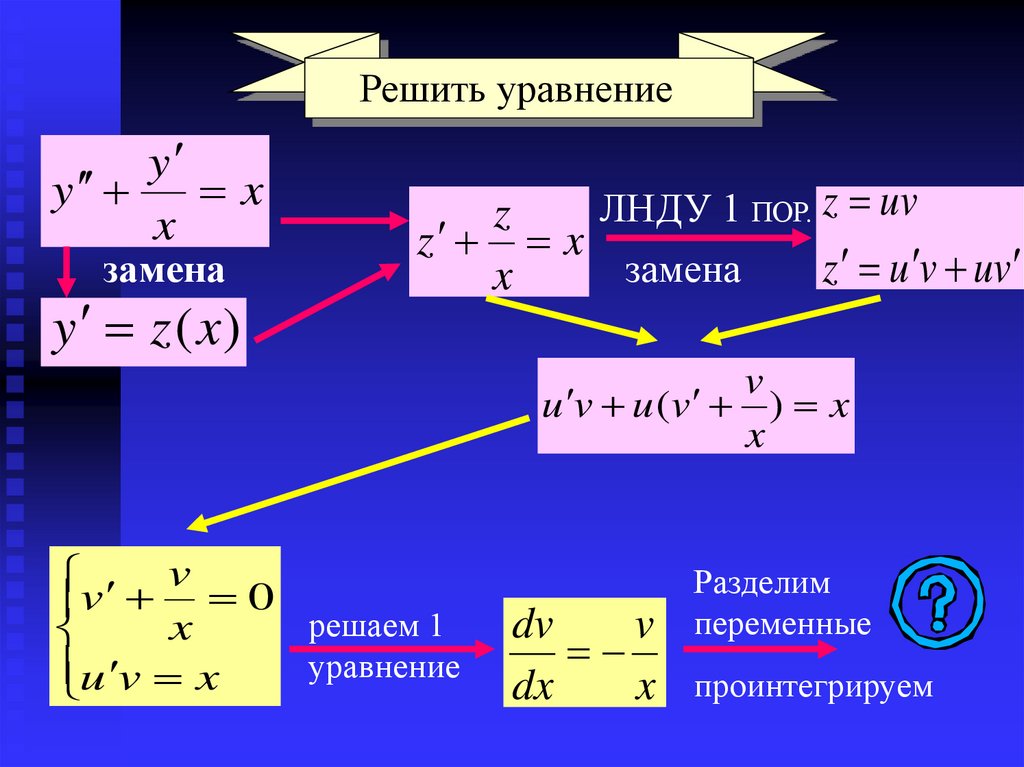
Решить уравнение
y
y
x
x
замена
y z (x )
ЛНДУ 1 ПОР. z uv
z
z x
замена
z u v uv
x
v
u v u (v ) x
x
v
v 0
решаем 1
x
уравнение
u
v
x
dv
v
dx
x
Разделим
переменные
проинтегрируем

15.

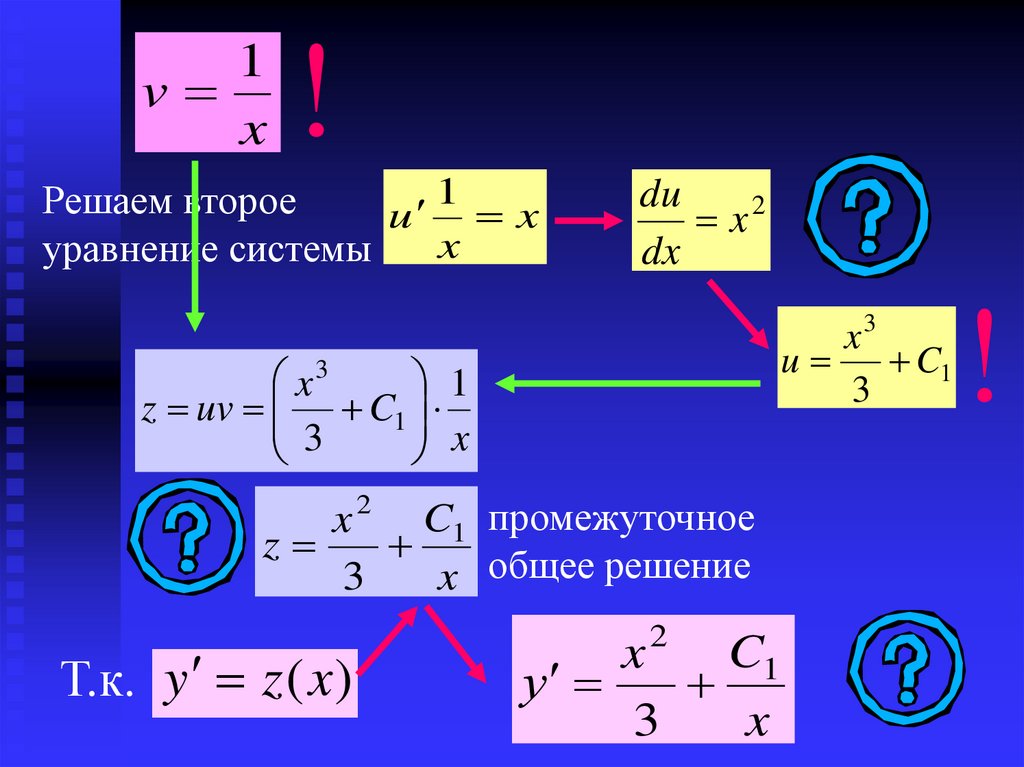
1
v
x
!
1
Решаем второе
u
x
x
уравнение системы
du
x2
dx
x3
u
C1
3
x3
1
z uv C1
3
x
x 2 C1 промежуточное
z
3
x общее решение
Т.к. y z (x )
2
C1
x
у
3
x
!

16.

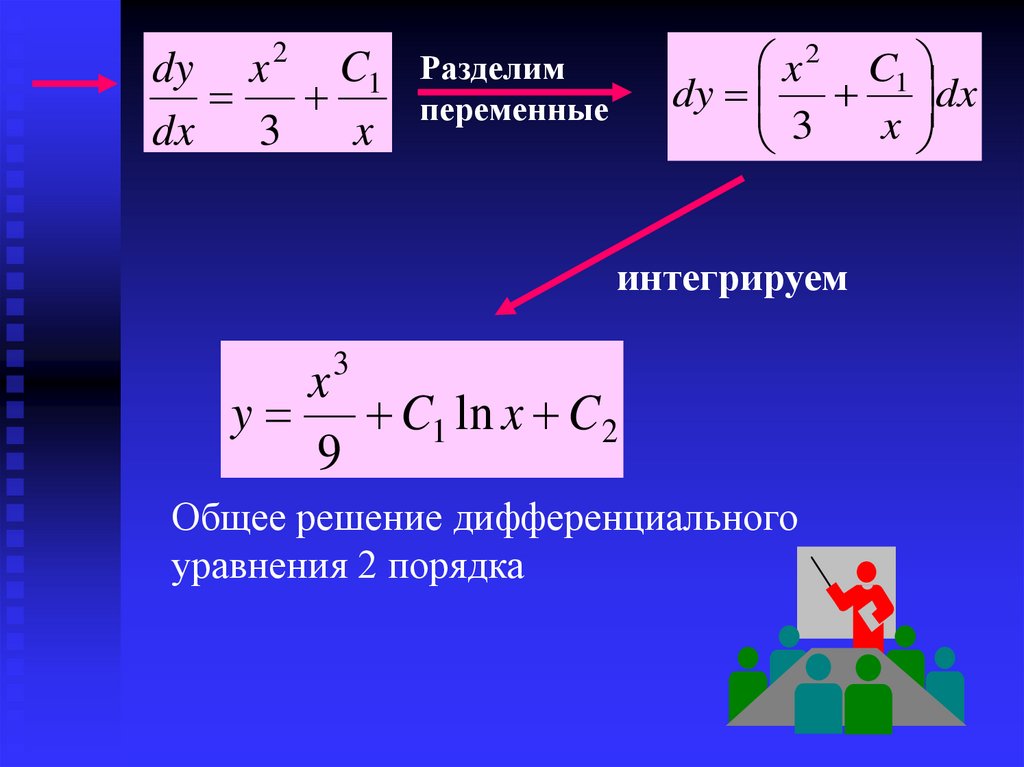
dy x 2 C1
dx 3
x
x 2 C1
dy dx
x
3
Разделим
переменные
интегрируем
3
x
y C1 ln x C 2
9
Общее решение дифференциального
уравнения 2 порядка

17.

2.3. Решение уравнений вида, y f ( y; y )
не содержащего независимой переменной
СХЕМА РЕШЕНИЯ
ВИД УРАВНЕНИЯ
y f ( y; y )
u(y)=u(y(x))неизвестная функция
Методы
решения
ДУ 1
порядка
Производная
сложной функции
du
u f ( y; u ) u ( y; C1 )
dy
Замена
y u( y)
y u ( y ) y
Уравнение с разделяющимися
переменными y ( y; C1 )

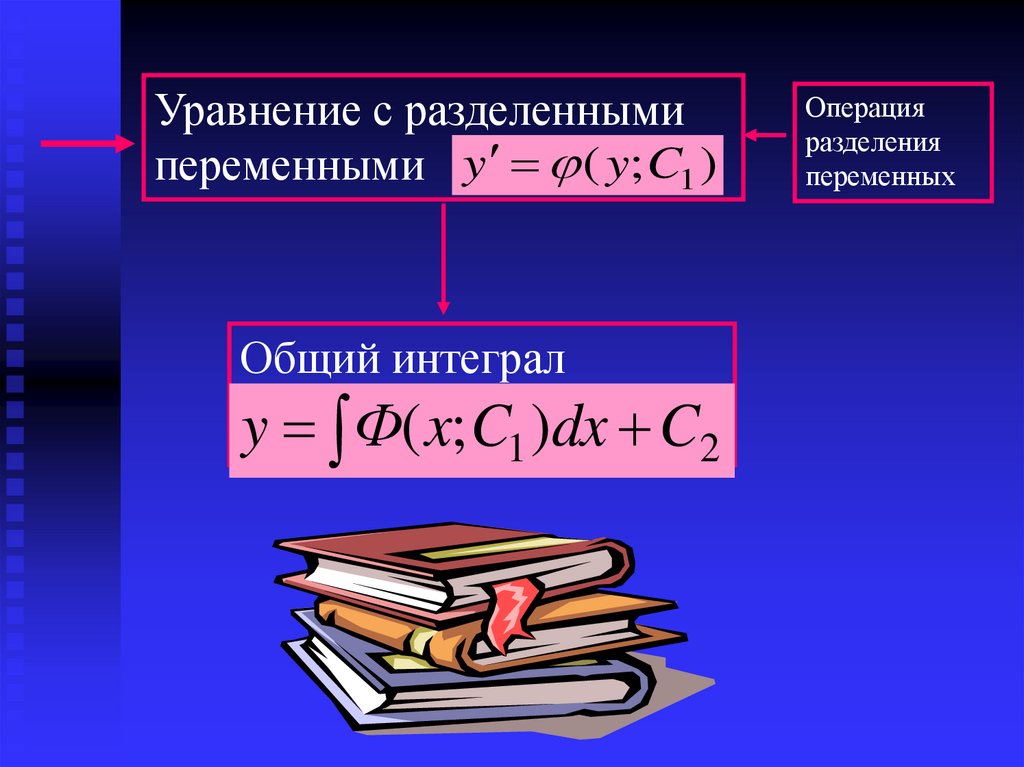
18.

Уравнение с разделенными
переменными y ( y; C1 )
Общий интеграл
y Ф( x; C1 )dx C2
Операция
разделения
переменных

19.

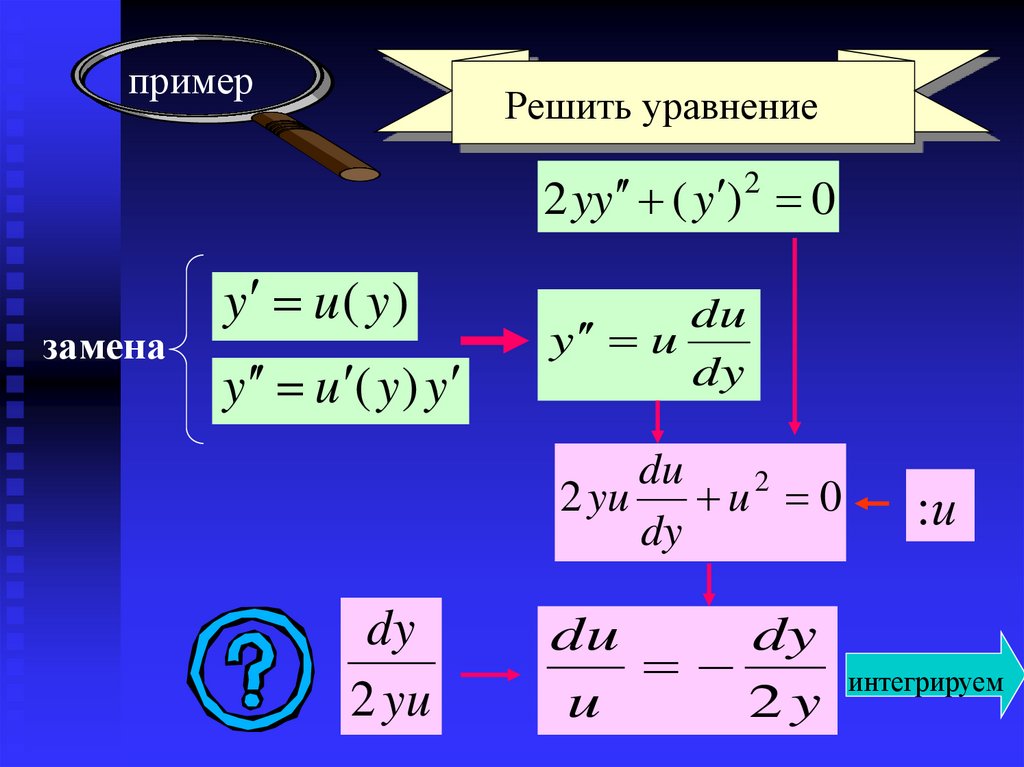
пример
Решить уравнение
2 yy ( y ) 2 0
замена
y u( y)
y u ( y ) y
du
y u
dy
du
2 yu
u2 0
dy
dy
2 yu
:и
du
dy
интегрируем
u
2y

20.

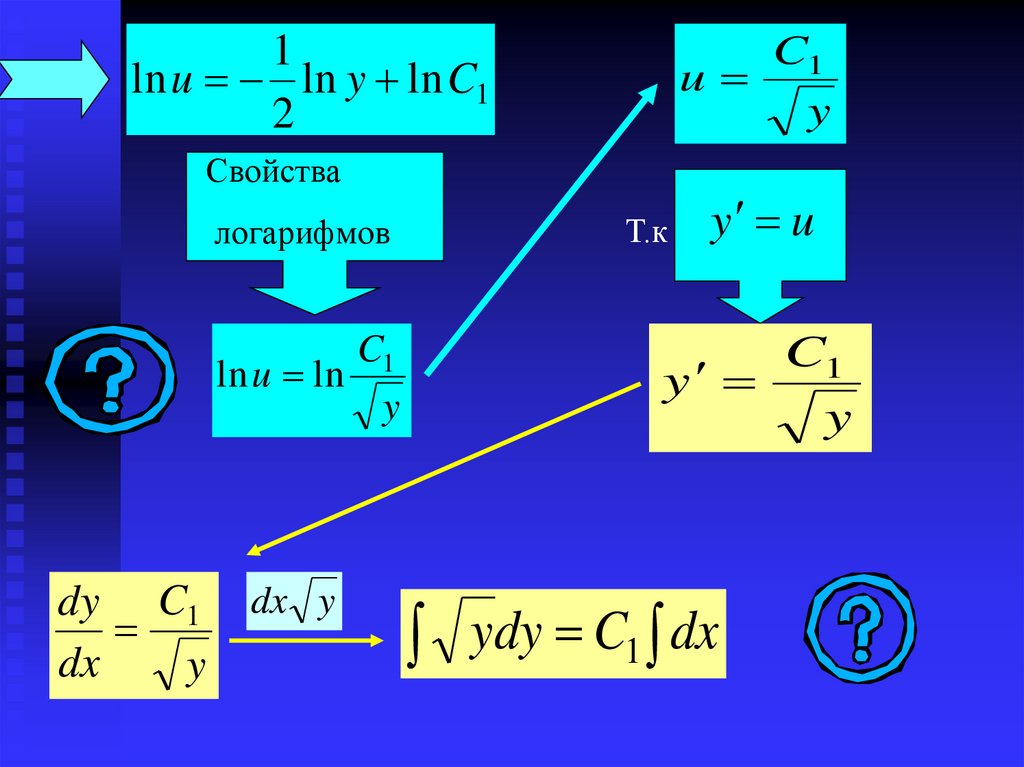
1
ln u ln y ln C1
2
C1
u
y
Свойства
логарифмов
C1
ln u ln
y
dy C1
dx
y
dx y
Т.к
y u
C1
y
y
ydy C1 dx