МОВРпроект

1.

Прогнозирование террористических атак с
использованием моделей одномерных временных
рядов
Выполнили: студенты группы ИСТ-АДМО-301Б
Сагадиев А.И.
Мусин Д.Р.
Скрипникова Д.И.

2.

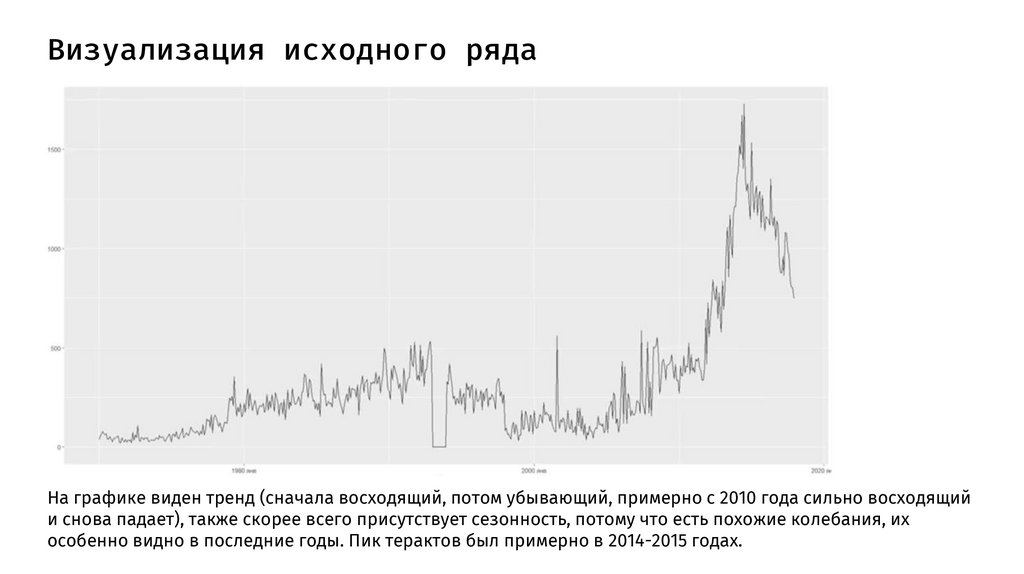
Визуализация исходного ряда
На графике виден тренд (сначала восходящий, потом убывающий, примерно с 2010 года сильно восходящий
и снова падает), также скорее всего присутствует сезонность, потому что есть похожие колебания, их
особенно видно в последние годы. Пик терактов был примерно в 2014-2015 годах.

3.

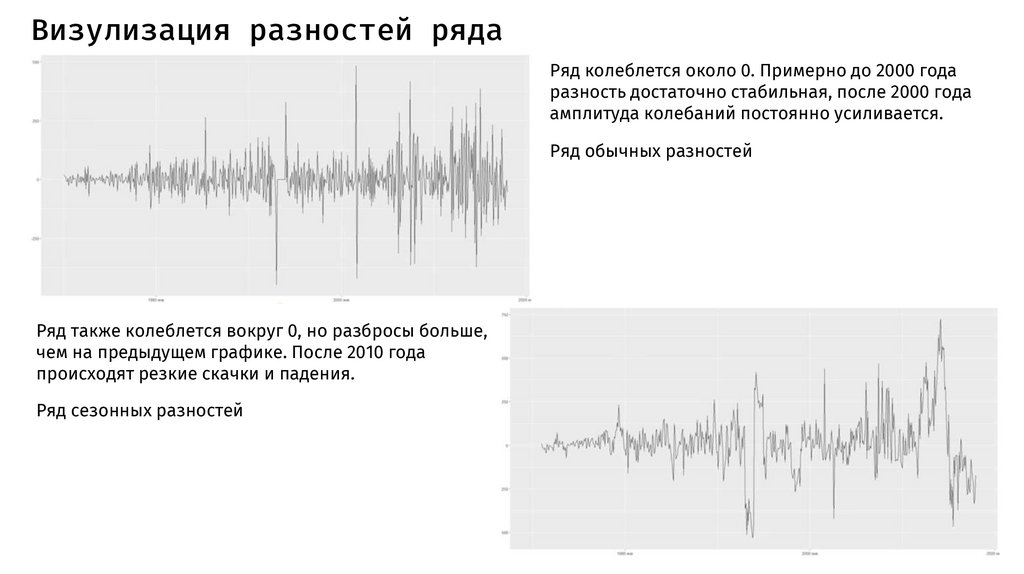
Визулизация разностей ряда
Ряд колеблется около 0. Примерно до 2000 года
разность достаточно стабильная, после 2000 года
амплитуда колебаний постоянно усиливается.
Ряд обычных разностей
Ряд также колеблется вокруг 0, но разбросы больше,
чем на предыдущем графике. После 2010 года
происходят резкие скачки и падения.
Ряд сезонных разностей

4.

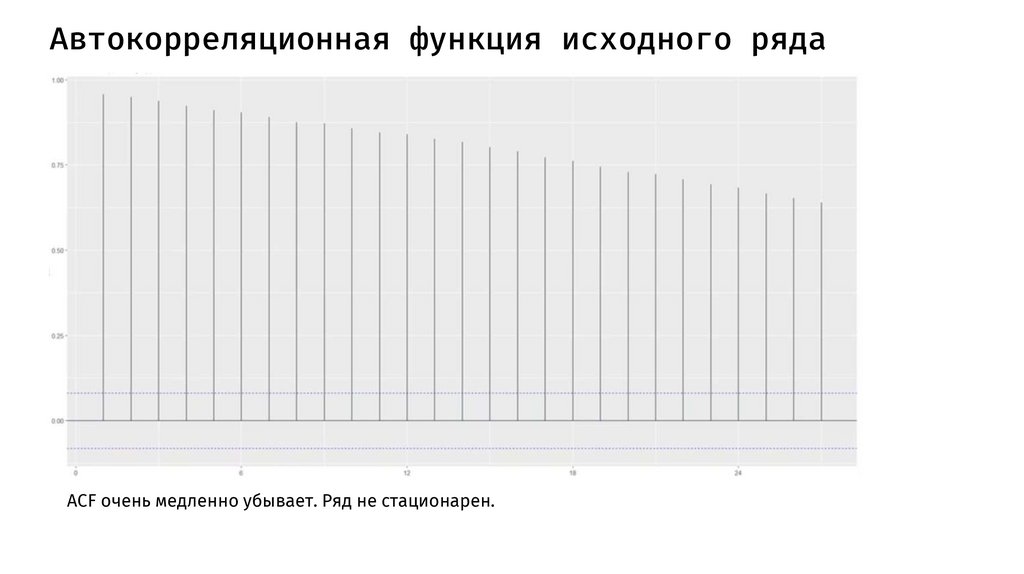
Автокорреляционная функция исходного ряда
ACF очень медленно убывает. Ряд не стационарен.

5.

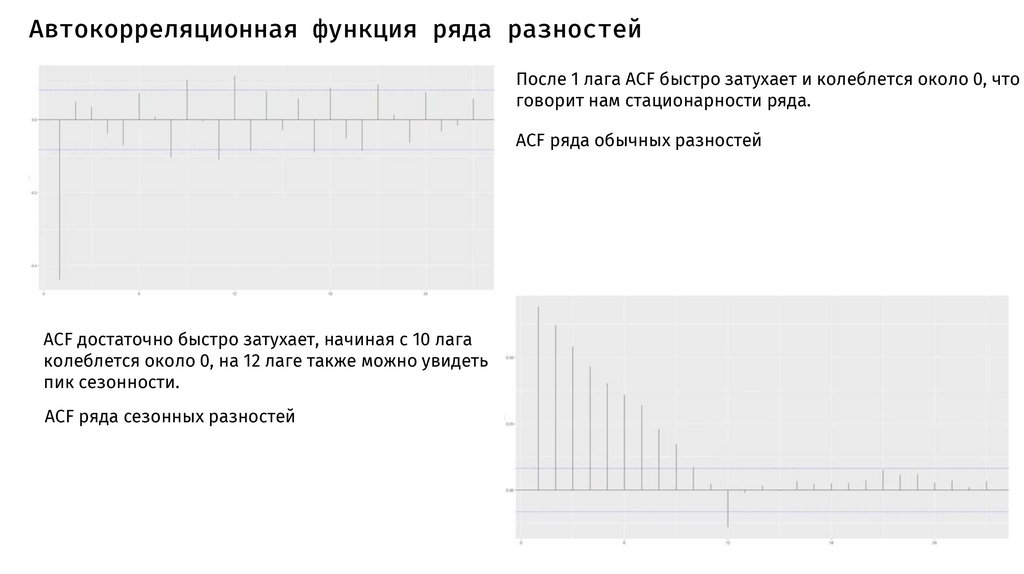
Автокорреляционная функция ряда разностей
После 1 лага ACF быстро затухает и колеблется около 0, что
говорит нам стационарности ряда.
ACF ряда обычных разностей
ACF достаточно быстро затухает, начиная с 10 лага
колеблется около 0, на 12 лаге также можно увидеть
пик сезонности.
ACF ряда сезонных разностей

6.

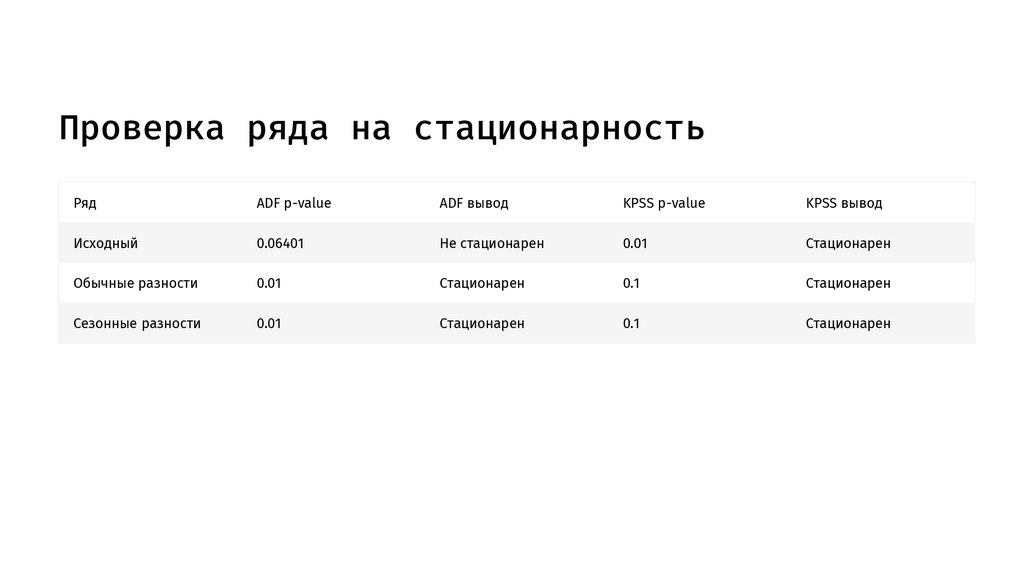
Проверка ряда на стационарность
Ряд
ADF p-value
ADF вывод
KPSS p-value
KPSS вывод
Исходный
0.06401
Не стационарен
0.01
Cтационарен
Обычные разности
0.01
Cтационарен
0.1
Cтационарен
Сезонные разности
0.01
Cтационарен
0.1
Cтационарен

7.

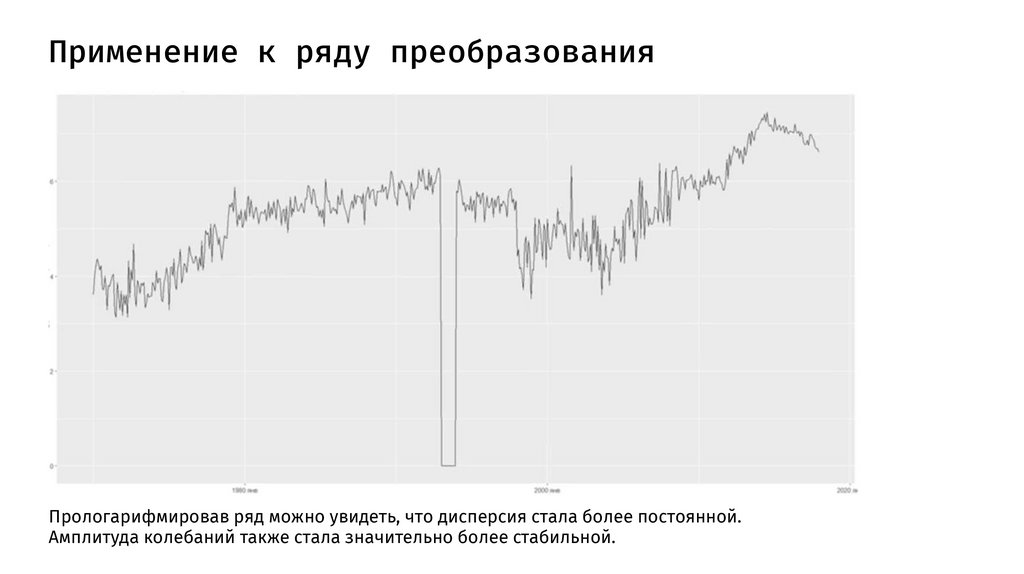
Применение к ряду преобразования
Прологарифмировав ряд можно увидеть, что дисперсия стала более постоянной.
Амплитуда колебаний также стала значительно более стабильной.

8.

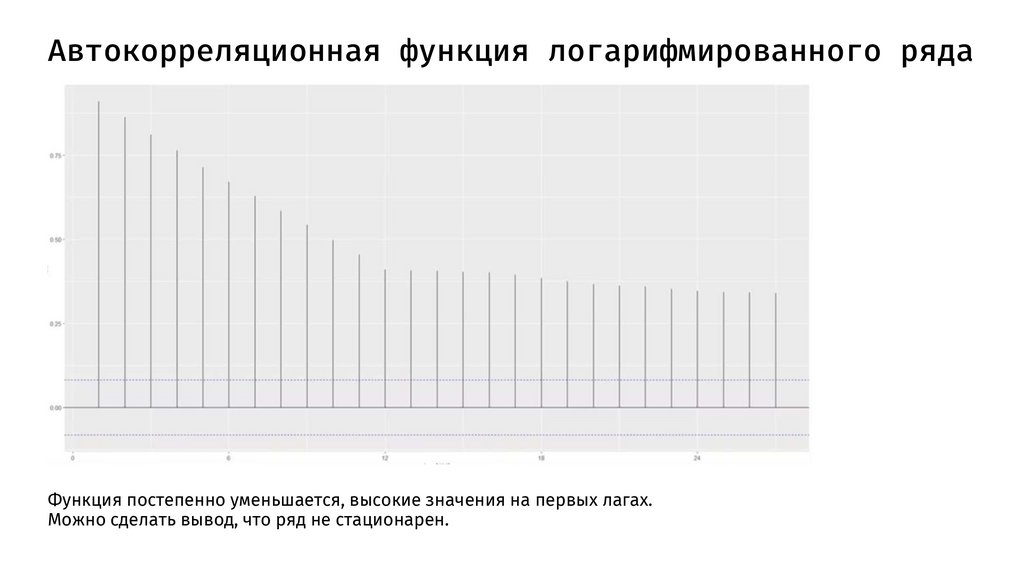
Автокорреляционная функция логарифмированного ряда
Функция постепенно уменьшается, высокие значения на первых лагах.
Можно сделать вывод, что ряд не стационарен.

9.

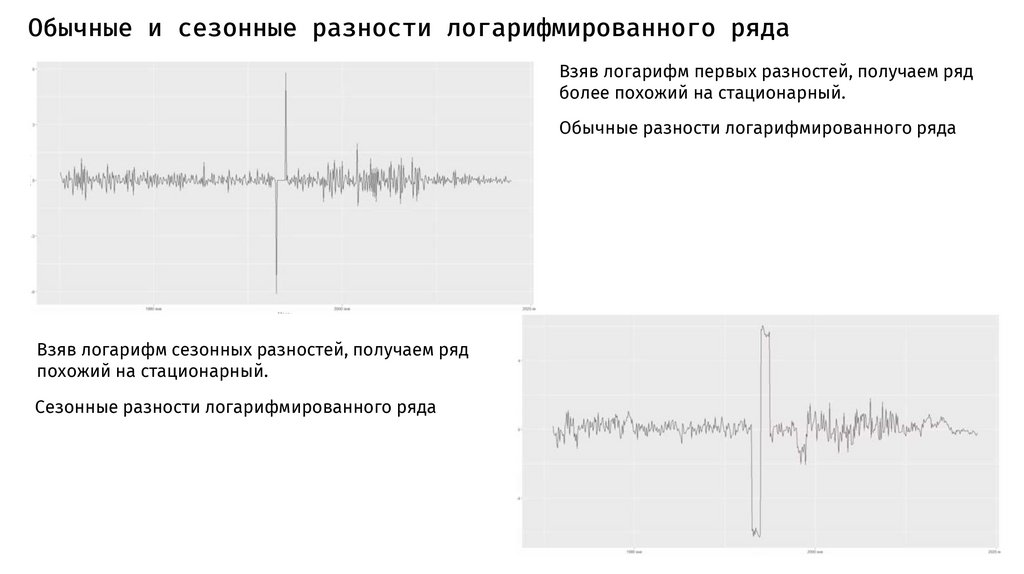
Обычные и сезонные разности логарифмированного ряда
Взяв логарифм первых разностей, получаем ряд
более похожий на стационарный.
Обычные разности логарифмированного ряда
Взяв логарифм сезонных разностей, получаем ряд
похожий на стационарный.
Сезонные разности логарифмированного ряда

10.

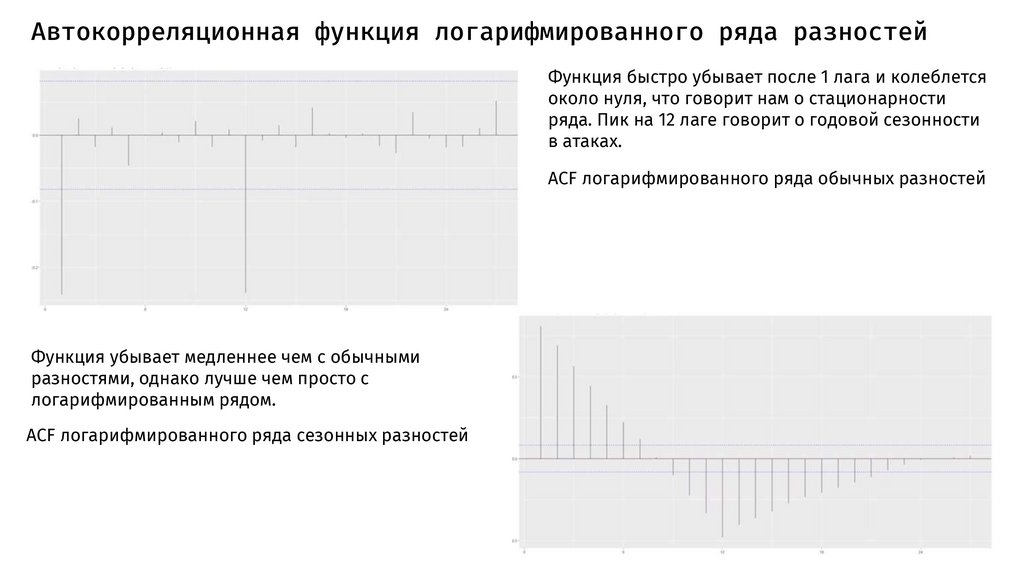
Автокорреляционная функция логарифмированного ряда разностей
Функция быстро убывает после 1 лага и колеблется
около нуля, что говорит нам о стационарности
ряда. Пик на 12 лаге говорит о годовой сезонности
в атаках.
ACF логарифмированного ряда обычных разностей
Функция убывает медленнее чем с обычными
разностями, однако лучше чем просто с
логарифмированным рядом.
ACF логарифмированного ряда сезонных разностей

11.

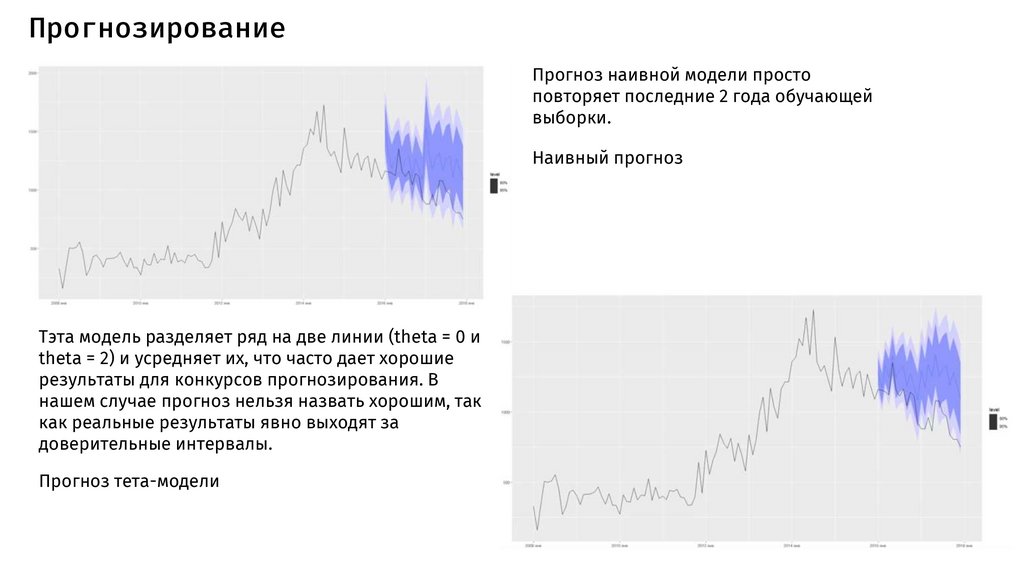
Прогнозирование
Прогноз наивной модели просто
повторяет последние 2 года обучающей
выборки.
Наивный прогноз
Тэта модель разделяет ряд на две линии (theta = 0 и
theta = 2) и усредняет их, что часто дает хорошие
результаты для конкурсов прогнозирования. В
нашем случае прогноз нельзя назвать хорошим, так
как реальные результаты явно выходят за
доверительные интервалы.
Прогноз тета-модели

12.

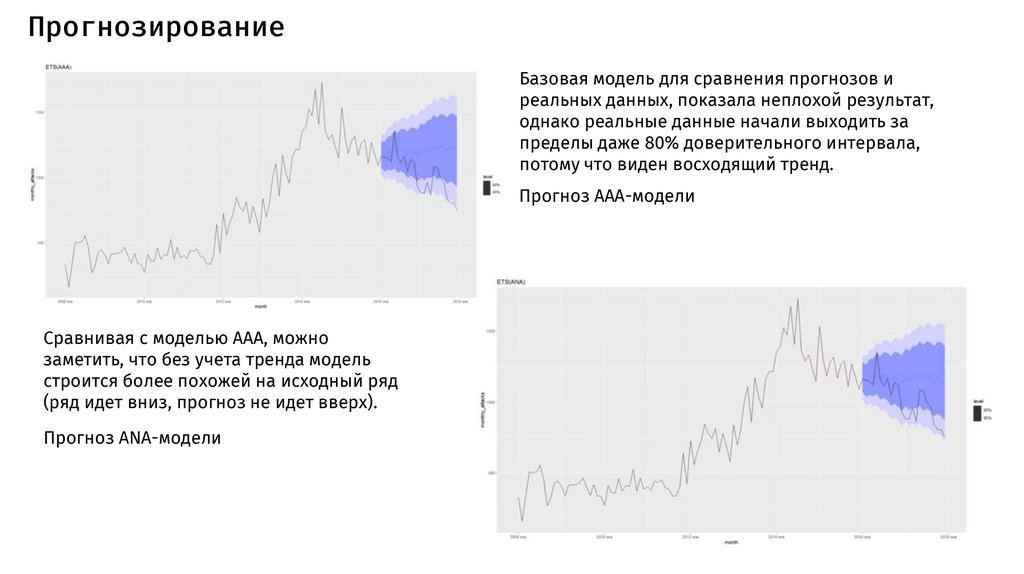
Прогнозирование
Базовая модель для сравнения прогнозов и
реальных данных, показала неплохой результат,
однако реальные данные начали выходить за
пределы даже 80% доверительного интервала,
потому что виден восходящий тренд.
Прогноз AAA-модели
Сравнивая с моделью ААА, можно
заметить, что без учета тренда модель
строится более похожей на исходный ряд
(ряд идет вниз, прогноз не идет вверх).
Прогноз ANA-модели

13.

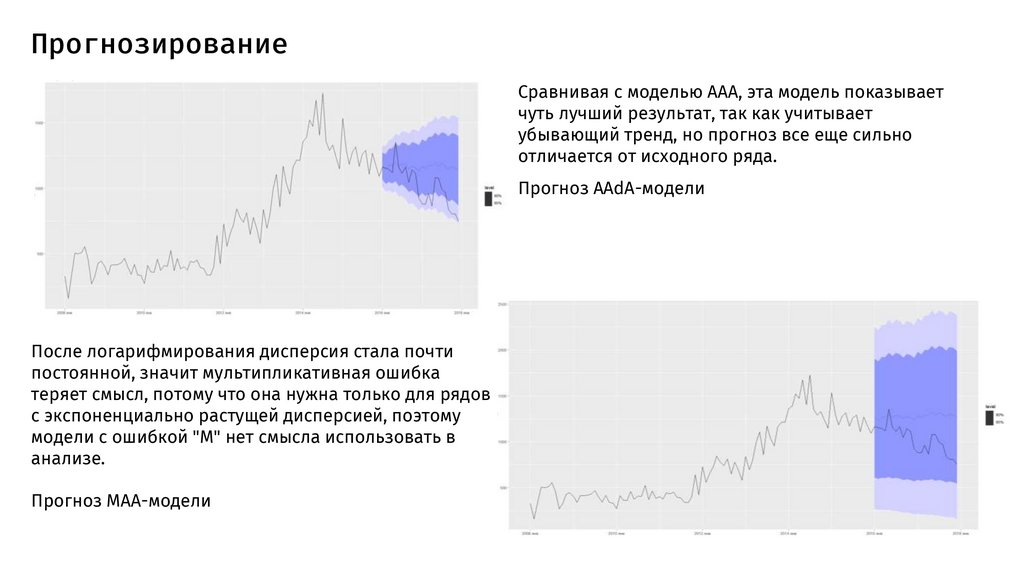
Прогнозирование
Сравнивая с моделью ААА, эта модель показывает
чуть лучший результат, так как учитывает
убывающий тренд, но прогноз все еще сильно
отличается от исходного ряда.
Прогноз AAdA-модели
После логарифмирования дисперсия стала почти
постоянной, значит мультипликативная ошибка
теряет смысл, потому что она нужна только для рядов
с экспоненциально растущей дисперсией, поэтому
модели с ошибкой "M" нет смысла использовать в
анализе.
Прогноз MAA-модели

14.

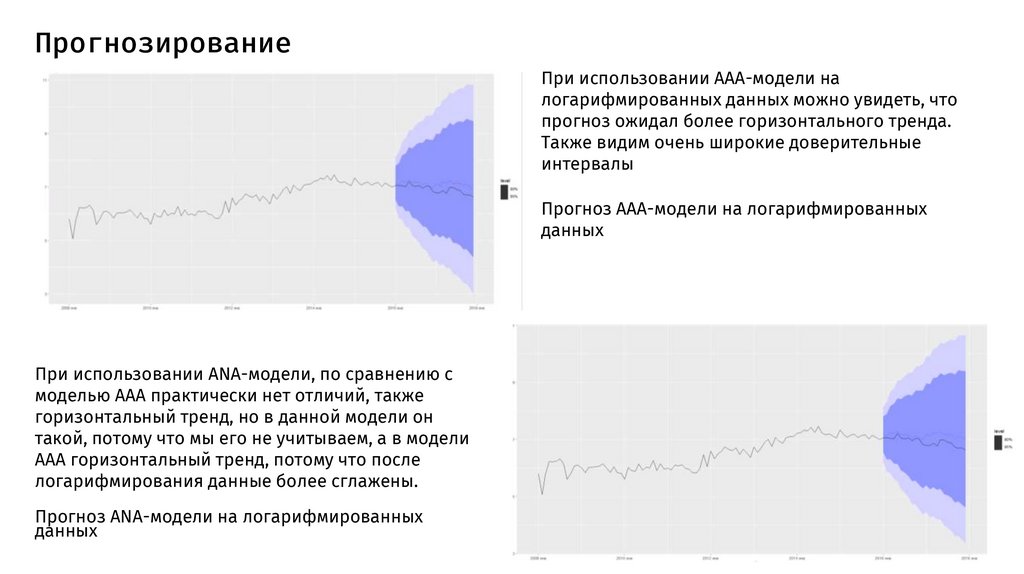
Прогнозирование
При использовании AAA-модели на
логарифмированных данных можно увидеть, что
прогноз ожидал более горизонтального тренда.
Также видим очень широкие доверительные
интервалы
Прогноз AAA-модели на логарифмированных
данных
При использовании ANA-модели, по сравнению с
моделью ААА практически нет отличий, также
горизонтальный тренд, но в данной модели он
такой, потому что мы его не учитываем, а в модели
ААА горизонтальный тренд, потому что после
логарифмирования данные более сглажены.
Прогноз ANA-модели на логарифмированных
данных

15.

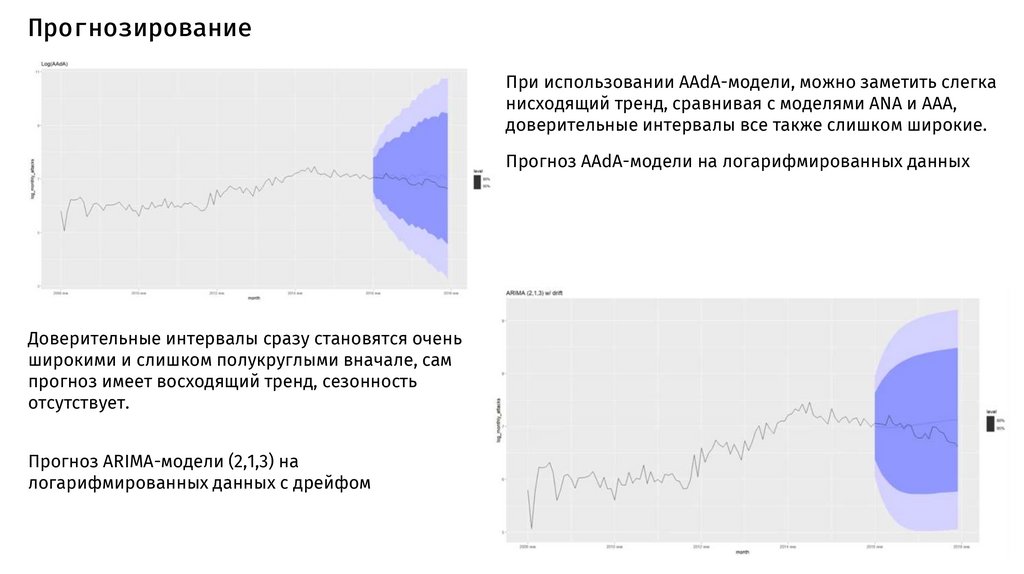
Прогнозирование
При использовании AAdA-модели, можно заметить слегка
нисходящий тренд, сравнивая с моделями ANA и AAA,
доверительные интервалы все также слишком широкие.
Прогноз AAdA-модели на логарифмированных данных
Доверительные интервалы сразу становятся очень
широкими и слишком полукруглыми вначале, сам
прогноз имеет восходящий тренд, сезонность
отсутствует.
Прогноз ARIMA-модели (2,1,3) на
логарифмированных данных c дрейфом

16.

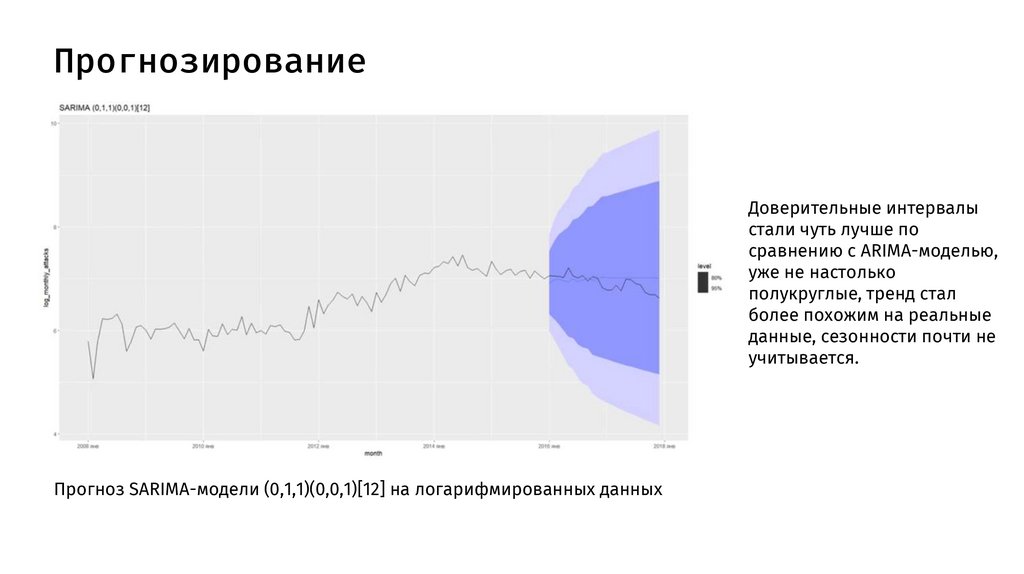
Прогнозирование
Доверительные интервалы
стали чуть лучше по
сравнению с ARIMA-моделью,
уже не настолько
полукруглые, тренд стал
более похожим на реальные
данные, сезонности почти не
учитывается.
Прогноз SARIMA-модели (0,1,1)(0,0,1)[12] на логарифмированных данных

17.

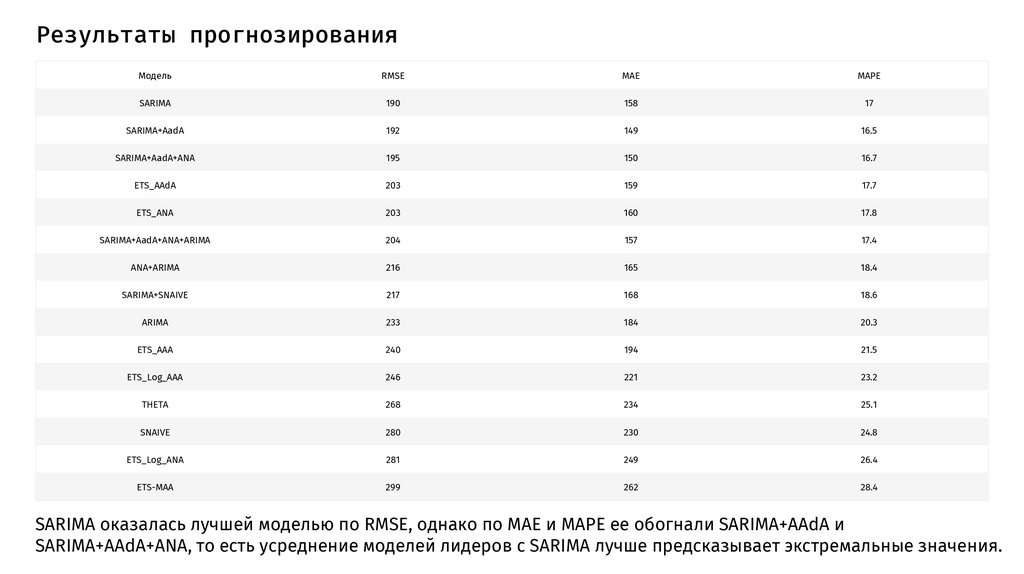
Результаты прогнозирования
Модель
RMSE
MAE
MAPE
SARIMA
190
158
17
SARIMA+AadA
192
149
16.5
SARIMA+AadA+ANA
195
150
16.7
ETS_AAdA
203
159
17.7
ETS_ANA
203
160
17.8
SARIMA+AadA+ANA+ARIMA
204
157
17.4
ANA+ARIMA
216
165
18.4
SARIMA+SNAIVE
217
168
18.6
ARIMA
233
184
20.3
ETS_AAA
240
194
21.5
ETS_Log_AAA
246
221
23.2
THETA
268
234
25.1
SNAIVE
280
230
24.8
ETS_Log_ANA
281
249
26.4
ETS-MAA
299
262
28.4
SARIMA оказалась лучшей моделью по RMSE, однако по MAE и MAPE ее обогнали SARIMA+AAdA и
SARIMA+AAdA+ANA, то есть усреднение моделей лидеров с SARIMA лучше предсказывает экстремальные значения.

18.

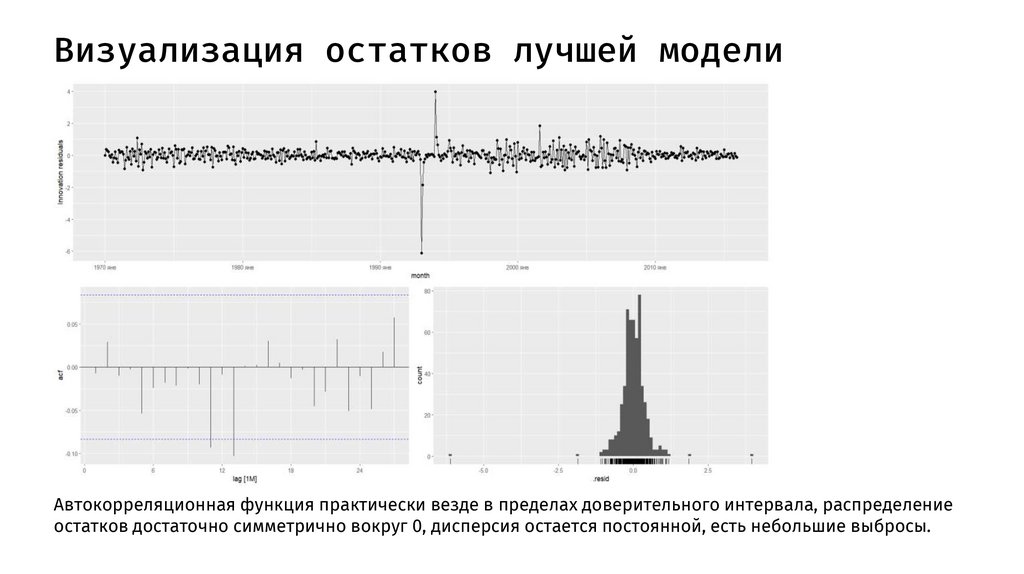
Визуализация остатков лучшей модели
Автокорреляционная функция практически везде в пределах доверительного интервала, распределение
остатков достаточно симметрично вокруг 0, дисперсия остается постоянной, есть небольшие выбросы.

19.

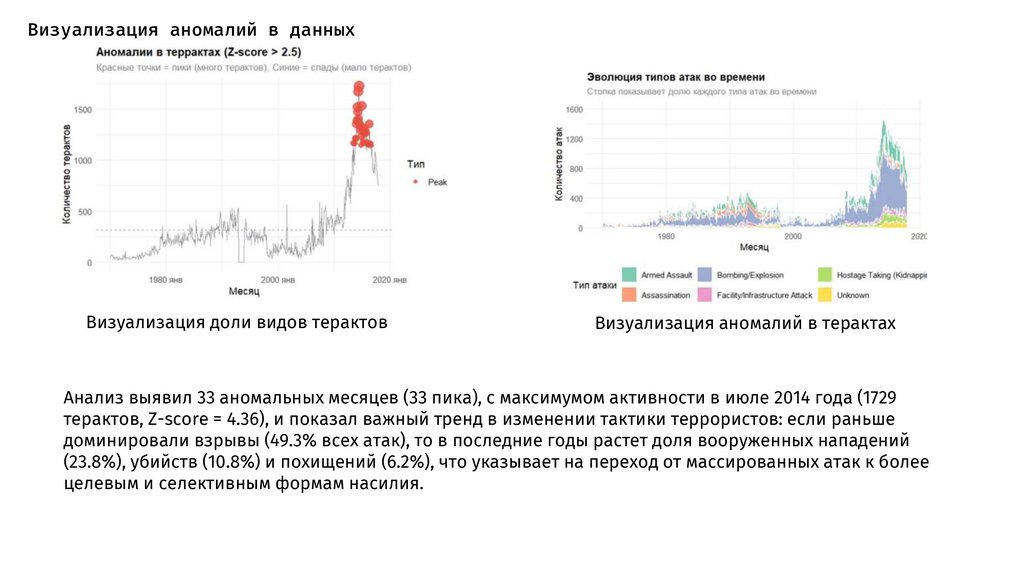
Визуализация аномалий в данных
Визуализация доли видов терактов
Визуализация аномалий в терактах
Анализ выявил 33 аномальных месяцев (33 пика), с максимумом активности в июле 2014 года (1729
терактов, Z-score = 4.36), и показал важный тренд в изменении тактики террористов: если раньше
доминировали взрывы (49.3% всех атак), то в последние годы растет доля вооруженных нападений
(23.8%), убийств (10.8%) и похищений (6.2%), что указывает на переход от массированных атак к более
целевым и селективным формам насилия.

20.

Вывод
Для стабилизации дисперсии применено логарифмирование с единичным сдвигом log(x+1), а данные
разделены на обучающую выборку (1970-декабрь 2015) и тестовую (2016-2017). На основе тестовой выборки
было построено и сравнено 14 моделей прогнозирования, из которых SARIMA(0,1,1)(0,0,1) показала лучший
результат с RMSE=190, MAE=158, MAPE=17%, остатки которой распределены нормально с отсутствием
автокорреляции. Дополнительный анализ аномалий методом Z-score выявил 33 аномальных периода с
пиком активности в июле 2014 года (1729 терактов) и показал эволюцию тактики террористов: доля
взрывов снижается с 49.3%, в то время как растут вооруженные нападения (23.8%), убийства (10.8%) и
похищения (6.2%). Таким образом, исследование демонстрирует, что террористическая активность имеет
четкие временные структуры, успешно моделируемые методами SARIMA, однако полученные модели
следует использовать как вспомогательный инструмент в сочетании с качественным анализом
геополитических факторов для полного понимания глобального терроризма.