2025_11_03_L09_AngularMomentum_Rotation

1.

Общая Физика. Механика
Лекция 09
Моменты импульса и силы.
Вращательное движение
Лектор:
Профессор НИЯУ МИФИ
Ольчак Андрей Станиславович(

2.

Момент импульса. Плечо импульса
Моментом импульса частицы относительно точки отсчета называют
векторное произведение радиус-вектора на импульс частицы:
M O r , p r , mv
M rp sin lp
M p
M r
ex e y ez
M r , p x
y
z
px p y pz
yp z zp y ex xpz zp x e y xpy yp x ez
Плечо импульса относительно точки 0 = длина
перпендикуляра, опущенного из точки O на
прямую, вдоль которой направлен вектор импульса
l r sin

3.

Момент импульса. Полярные координаты.
Момент импульса мат. точки относительно точки отсчета 0:
M O r , p r , mv
M p
M r
M rp sin lp
l r sin
Связь полярных и декартовых координат и компонент скорости
точки на плоскости: x = r cos φ ; y = r sin φ; r2 = x2 + y2 ; tg φ = y/x
v2 = vx2 + vy2 = vφ2 + vr2
vr= dr/dt = (r,v)/r ; vφ = rdφ/dt = rωz = [vr 2 - vr 2 ]1/2
v = [r,ω]; ω = [r,v]/r2 ; ωz=dφ/dt=угловая скорость движения точки

4.

Момент импульса. Полярные координаты.
Момент импульса мат. точки относительно точки отсчета 0:
M O r , p r , mv
v = [r,ω]
ω = [r,v]/r2
M = [r, p] = m[r [r, ω]] = mr2ω ; M || ω ; ωz=dφ/dt
Если точка массы m, движется вокруг оси OZ по
окружности радиуса r, ее момент импульса
Mz = mr2ωz = Izωz ; Iz = mr2 – момент инерции мат .точки
массы m, относительно оси вращения Z

5.

Момент импульса. ПРИМЕРЫ
1. Частица массы m движется по прямой со
скоростью v. Модуль момента импульса равен
M = mvl, причем плечо l остается
неизменным.
СЛЕДСТВИЕ: если на частицу не действуют силы
– ее момент импульса не меняется ни по величине,
ни по направлению: M = [r, p]
2. Частица движется по окружности радиуса r со
скоростью v. Момент импульса относительно
центра вращения направлен перпендикулярно
плоскости вращения и равен Mz = mvr. = mr2ωz.

6.

Момент силы. Плечо силы.
Момент силы F относительно точки О, из которой
проведен радиус-вектор r к точке приложения силы:
N [r , F ]
1. Вектор N перпендикулярен векторам r и F, образуя с ними правую тройку.
2. Модуль момента силы можно представить в виде N = r F·sinα =l·F,
где l= r·sinα – плечо силы относительно точки O = длина перпендикуляра, опущенного
из точки О на прямую, вдоль которой действует сила
3. Точку приложения силы (к протяженному твердому телу) можно сдвигать вдоль линии
действия силы: ни l ни N при этом не изменятся.
4. Величина и направление N зависят от выбора точки О

7.

Пара сил.
Пара сил = две равные по модулю противоположно направленные силы, не
действующие вдоль одной прямой. Расстояние между прямыми, вдоль которых
действуют силы L = плечо пары. Суммарный момент сил, образующих пару,
равен:
N [r1 , F1 ] [r2 , F2 ]
F1 F2
N [r1 , F2 ] [r2 , F2 ] [ r2 r1 , F2 ]
N [l , F ]
l r2 r1
l = вектор, проведенный из точки приложения силы F1 в точку приложения силы F2
Момент пары сил не зависит от выбора точки отсчета O. Вектор момента пары сил
перпендикулярен к плоскости, в которой лежат силы, и численно равен
произведению модуля любой из сил на плечо пары сил N = FL.

8.

Производная момента импульса по времени
dM d dr dp dp
r , p , p r , v , p r ,
dt
dt
dt dt
dt
dp
p || v [v , p] 0
F
dt
dM
r, F N
dt
Производная по времени от момента импульса тела относительно
некоторой точки равна моменту действующей на тело силы
относительно той же точки.

9.

Момент импульса системы материальных точек
Момент импульса системы относительно точки = векторная сумма
моментов импульса всех частиц, входящих в систему:
M сист M i ri , pi
i
Для каждой частицы:
i
dM i
N i N ij
dt
j , j i
Первое слагаемое – момент внешних сил, действующих на i-ую
частицу, а второе – сумма моментов внутренних сил. Суммируя по всем
частицам, получаем:
dM сист
dM i
N i N ij
dt
dt
i
i
i j , j i

10.

Закон сохранения момента импульса
dM сист
dM i
N i N ij
dt
dt
i
i
i j , j i
Двойная сумма в правой части уравнения обращается в нуль, т.к. содержит
парные слагаемые вида:
ri , Fij r j , F ji ri rj , Fij
Fij F ji
Закон изменения суммарного момента
импульса системы взаимодействующих тел:
скорость изменения момента импульса
системы равна суммарному моменту
внешних сил, действующих на систему:
dM сист
Ni
dt
i
[ri r j , Fij ] 0

11.

Закон сохранения момента импульса
Уравнение для моментов: производная по
времени от полного момента импульса системы
равна результирующему моменту внешних сил.
При отсутствии
внешних сил
dM сист
Ni
dt
i
Момент импульса замкнутой
dM / dt 0 системы M сохраняется
Закон сохранения момента импульса: момент импульса
замкнутой системы материальных точек остается постоянным.
Момент импульса остается постоянным и для незамкнутой
системы при условии, что суммарный момент внешних сил
равен нулю.

12.

Движение в центральном поле сил
Поле сил называют центральным, если силы, действующие на попавшее под их
действие тело в любой точке направлены на центр поля, а модуль силы зависит
только от расстояния до этого центра.
r
F f r er f r
r
r
NO r , F r , f r 0 Момент импульса частицы относительно
r
центра (т. 0) будет сохраняться
M O r, mv const
Момент M перпендикулярен к плоскости,
образованной векторами r и p => плоскость
движения фиксирована!
При движении тела в центральном поле сил его радиус-вектор остается все
время в одной плоскости. В этой же плоскости остается и вектор p.
Траектория движения тела = плоская кривая.

13.

Движение в центральном поле сил. ПРИМЕР
Силы, обратно пропорциональные квадрату расстояния от центра
f r 2 , const
r
dr
U 2 C , U 0 C 0
r
r
mr 2 mr 2 2
2 2
E
M
mr
z
2
2
r
mr 2 M z const
2
mr mr
2 E const
r
2
2
2
r t , t

14.

Движение в центральном поле сил. ПРИМЕР
Силы, обратно пропорциональные квадрату расстояния от центра
f r 2 , const
r
mr 2 M z const
2
mr mr
2 E const
r
2
2
2
r t , t
Траектория частицы = коническое сечение, т.е. либо эллипс, либо
парабола, либо гипербола.
α > 0 (отталкивание): Гипербола. При Mz= 0 вырождается в прямую
α < 0 (притяжение): Эллипс при E < 0, гипербола при E > 0, парабола
при E = 0

15. Связь законов сохранения со свойствами пространства и времени.

Основные свойства
пространства
и времени
Законы сохранения,
вытекающие из этих
свойств
Однородность времени
Закон сохранения энергии
Однородность
пространства
Закон сохранения
импульса
Изотропность
пространства
Закон сохранения момента
импульса
Ландау Л.Д., Лифшиц Е.М. «Механика», гл.2

16.

Механика твердого тела
Вращательное движение
Механика твердого тела

17.

Твердое тело. Формы движения. Поступательное
Твердое тело = протяженное тело, расстояние между любой парой
точек которого в процессе движения остается неизменными.
Поступательное движение твердого тела: движение, при котором
прямая, проведенная между любой парой точек, принадлежащих телу,
при движении остается параллельной самой себе. Для описания
поступательного движения достаточно следить за одной (любой)
точкой, принадлежащей телу (например, за его центром масс).
Центр масс твердого тела движется так же, как двигалась бы мат. точка
равной массы под действием всех приложенных к телу внешних сил.

18.

Твердое тело. Формы движения. Вращательное
Вращение твердого тела вокруг неподвижной оси
φ
При вращении твердого тела вокруг закрепленной
оси все его точки движутся по окружностям с
центрами на оси вращения.
Тело при этом не обязательно должно совершать
полные обороты. Возможны просто колебания.
Достаточно следить за одной координатой - углом
поворота φ по отношению к некоторой опорной оси..

19.

Связь угловой и линейной скорости
Угловая скорость вращения ω = dφ/dt [с-1 ]
– псевдо-вектор, направленный вдоль оси
вращения - по правилу правого винта.
Линейная скорость v точки, положение которой задается
радиус-вектором r: v = [ω,r] = Rω
R – расстояние от точки до оси вращения
Линейная скорость точки при вращательном движении всегда
направлена по касательной к траектории движения (окружности).
Угловое ускорение: β = dω/dt
[рад/с2] = [с-2 ]

20.

Момент импульса вращающейся точки
Момент импульса мат. точки отн. т. О и оси ОZ:
M O r , p r , mv
M = [r, p] = m[r [r, ω]] = mr2ω
M || ω ; ωz= dφ/dt
Если точка массы m, движется вокруг оси OZ по
окружности радиуса R, ее момент импульса
Mz = mR2ωz = Izωz ; Iz = mR2 – момент инерции мат .точки
массы m, относительно оси вращения Z (элементарный момент
инерции точки. R – расстояние до оси вращения

21.

Момент импульса твердого тела
при вращении вокруг неподвижной оси
Момент импульса элементарной массы dm относительно оси OZ:
Mi = Ri Pi = Ri dmi Riωz = ωzdmiRi2
Момент импульса всего тела
относительно оси OZ :
Mz = ωzΣdmiRi2 = ωzIz ,
Iz - момент инерции вращения
твердого тела относительно оси OZ
Переходим от суммы к интегрированию и вычисляем момент инерции
как интеграл по всему объему тела от плотности массы , которая в
разных точках может быть разной.:
Iz = Σ mi Ri2 = ∫ρ(r)r2dV

22.

Моменты инерции
для некоторых симметричных тел
Момент инерции твердого тела относительно оси вращения OZ
можно представить в виде суммы или интеграла
Iz = Σ dmi Ri2 = ρ(r)Rr2dV
Для одной мат. точки массы m,
вращающейся на расстоянии R
от оси OZ, момент инерции очевидно раве
Iz = mR2
Найдем далее моменты инерции для некоторых симметричных тел

23.

Моменты инерции
для некоторых симметричных тел
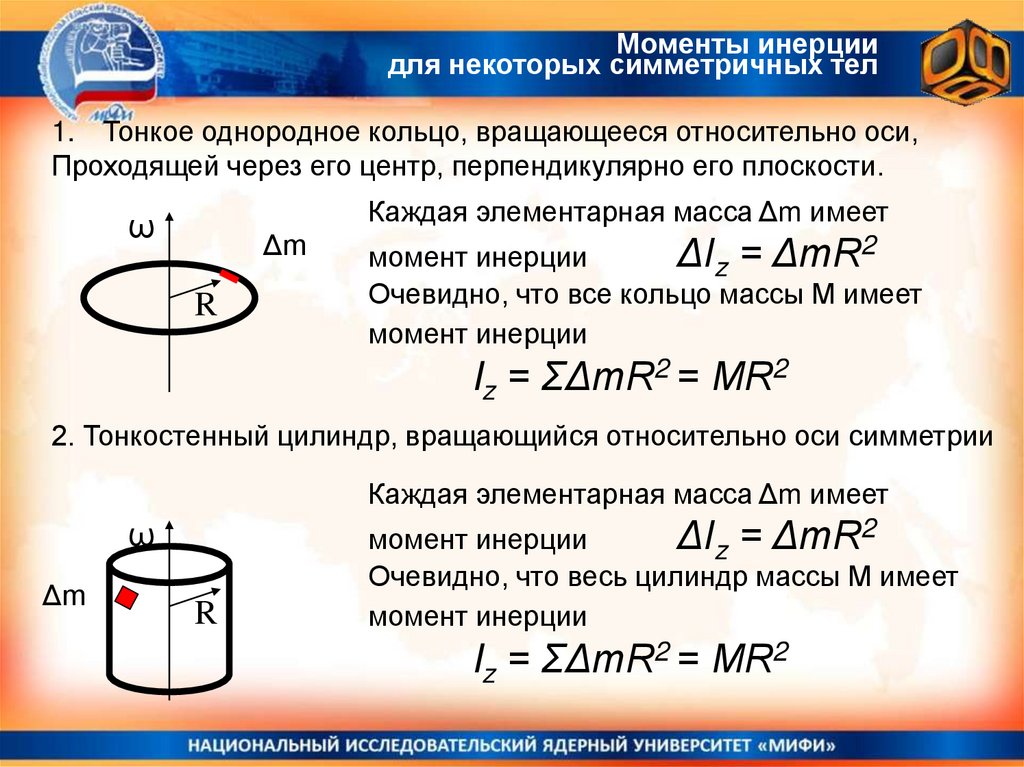
1. Тонкое однородное кольцо, вращающееся относительно оси,
Проходящей через его центр, перпендикулярно его плоскости.
Каждая элементарная масса Δm имеет
ω
Δm
R
момент инерции
ΔIz = ΔmR2
Очевидно, что все кольцо массы М имеет
момент инерции
Iz = ΣΔmR2 = МR2
2. Тонкостенный цилиндр, вращающийся относительно оси симметрии
Каждая элементарная масса Δm имеет
ω
Δm
R
момент инерции
ΔIz = ΔmR2
Очевидно, что весь цилиндр массы М имеет
момент инерции
Iz = ΣΔmR2 = МR2

24.

Моменты инерции
для некоторых симметричных тел
ω
3. Однородный цилиндр с плотностью вещества ρ,
вращающийся вокруг оси симметрии.
L
Возьмем вложенный тонкостенный цилиндр
r = r+dr
Его момент инерции dIz = dmr2 = ρL2πr3dr
с массой dm = ρL2πrdr
R
Момент инерции всего цилиндра находим,
интегрируя по всем тонкостенным цилиндрам
с радиусами от 0 до R:
M = ρLπR2
Iz = 2πLρ
r3dr = πLρR4/2 =
= MR2/2

25.

Моменты инерции
для некоторых симметричных тел
4. Тонкостенная сфера массы М и радиуса R, вращаюω, Z
щаяся вокруг оси OZ, проходящей через ее центр.
Разобьем сферу мысленно на множество тонких
перпендикулярных оси OZ колец шириной Rdθ
θ
и с радиусами r = Rsinθ, зависящими от угла θ,
o R
под которым кольцо видно из центра сферы.
Каждое кольцо имеет момент инерции, равный
dIz = (dm)R2sin2θ
Массы колец пропорциональны их площадям поверхности:
dm = М 2πR|sinθ| Rdθ / 4πR2 = М|sinθ|dθ / 2
Интегрируя по всем кольцам (2 раза по dθ от 0 до π/2), находим:
π/2
0
Iz = MR2 sin3θdθ = MR2 (1 - cos2θ)d(-cosθ) = 2MR2/3
0
-1

26.

Моменты инерции
для некоторых симметричных тел
ω, Z
5. Однородный шар с плотностью вещества ρ,
вращающийся вокруг оси симметрии.
r - r+dr
o R
Возьмем вложенную тонкостенную сферу
с массой dm = ρ4πr2dr
Ее момент инерции dIz = 2(dm)r2 /3= 8πρr4(dr)/3
Момент инерции всего шара находим,
интегрируя по всем тонкостенным сферам
с радиусами от 0 до R:
M = ρ4πR3/3
Iz = (8/3)πρ
r4dr = 8πρR5/15 =
= 2MR2/5

27.

Моменты инерции
для некоторых симметричных тел
6. Однородный тонкий стержень длины и массы М,
вращающийся вокруг оси перпендикулярной ему
и проходящей через конец стержня
ri
dmi
ω
Разобьем мысленно стержень на элементарные
массы
dmi = Mdr/L
Каждая элементарная масса имеет момент
инерции
dIz = (dm)r2 = Mr2dr/L
Момент инерции всего стержня находим,
интегрируя по всем элементарным массам
с расстояниями до центра вращения от 0 до L:
Iz = (M/L)
r2dr = ML2/3

28.

Моменты инерции
для некоторых симметричных тел
1. Материальная точка, вращающаяся
вокруг оси на расстоянии R от нее:
Iz = MR2
2. Кольцо и тонкостенный цилиндр, радиуса R,
вращающиеся вокруг оси симметрии
Iz = MR2
3. Однородный цилиндр радиуса R,
вращающийся вокруг оси симметрии
Iz = MR2/2
4. Тонкостенная сфера радиуса R,
вращающаяся вокруг оси симметрии
Iz = 2MR2/3
5. Однородный шар радиуса R,
вращающийся вокруг оси симметрии
Iz = 2MR2/5
6. Однородный тонкий стержень длины L,
вращающийся вокруг оси перпендикулярной ему
и проходящей через конец стержня
Iz = MR2/3

29.

Теорема
mi
Rci
C
Ri
o
a
Штайнера
Пусть нам известен момент инерции тела массы М
относительно оси, проходящей через центр масс С.
Найдем его момент инерции относительно
параллельной оси, проходящей через точку О,
отстоящую от С на радиус - вектор а.
IО = ΣmiRi2 = Σmi(Rci + a)2 = ΣmiRci2 + 2aΣmiRci +(Σmi)a2
ΣmiRci2 = IС ; 2aΣmiRci = 0 ; (Σmi)a2 = Ма2
IО = IС + Ма2
Момент инерции тела относительно произвольной оси равен его моменту
инерции относительно параллельной оси, проходящей через центр масс,
плюс произведение массы тела на квадрат расстояния между осями.

30.

Уравнение движения
для вращающегося твердого тела
Выразим момент импульса через момент
инерции тела в проекции на ось вращения OZ:
dM сист
Ni
dt
d(ωzIz)/dt = Izβz = ΣNiz
i
Здесь βz - угловое ускорение вращающегося тела в проекции на ось
вращения OZ; ΣNiz - сумма проекций всех моментов внешних сил на
ось вращения OZ.
Это уравнение движения для твердого тела, вращающегося
вокруг неподвижной оси = аналог второго закона Ньютона
для поступательного движения.

31.

Кинетическая энергия твердого тела при
вращении вокруг неподвижной оси
Кинетическая энергия твердого тела:
T = Σmivi 2/2
Линейная скорость i-ой точки:
vi = [ω,ri] ; vi = ωRi
T = Σdmivi 2/2 = ω2ΣdmiRi 2/2
ΣdmiRi 2 = Iz
=> T = Iz ω2/2

32.

Работа внешних сил при вращении
твердого тела вокруг неподвижной оси
Fi- сумма сил, действующих на точку mi
dAi = (Fi dri) - элементарная работа сил при перемещении точки на dri
dAi = (Fi dri) = (Fi [dφ,ri ]) = (dφ [ri , Fi,]) = (dφ, Ni) = NZ i dφ
Здесь NZ i - момент сил, действующих на данную мат. точку.
Твердое тело = множество мат. точек.
Суммируем по всем точкам, :
А = = NZ внешdφ, - NZ внеш - суммарный момент всех внешних сил,
действующих на все точки твердого тела

33.

Работа внешних сил при вращении
твердого тела вокруг неподвижной оси
fi- равнодействующая всех внутренних сил, действующих на mi
Fi- равнодействующая всех внешних сил, действующих на mi
fi+ Fi - равнодействующая всех сил, лежащая в плоскости вращения
dAi = (fi+Fi)dri -
элементарная работа всех сил;
Так как dri = [dφ,ri ]
dAi = (fi [dφ,ri ]) +(Fi [dφ,ri ])
После циклической перестановки векторов:
dAi = (dφ[fi ,ri ]) +(dφ[Fi,ri ])
Суммируем по всем элементарным массам:
dA=ΣdAi=(dφ,Σ[fi ,ri]) +(dφ,Σ[Fi,ri])=(dφ,ΣNi внутр) +(dφ,ΣNiвнеш )
Окончательно: dA = (dφ,ΣNi внеш ) = NZ внешdφ
При повороте на конечный угол: A =
NZ внешdφ

34.

35.

Курс общей физики НИЯУ МИФИ
Спасибо за внимание!
Продолжение следует.