Похожие презентации:
Динамика вращательного движения
1.
Движение центра инерции (массы) тела (системы тел)z
Представим тело (систему тел), как
систему N материальных точек с
массой m i , где i 1 N .
zc
Введем радиус-вектор некоторой точки C как
С
rc
1
rC m i ri
m i 1
N
mi – масса i-й материальной точки;
ri – радиус-вектор i-й м. т.
N
yc
0
m i
ri
xc
y
m m i - масса тела (системы тел).
i 1
1 N
x C m i x i
m i 1
1 N
yC m i y i
m i 1
1 N
zC m i z i
m i 1
Точка С называется центром инерции или центром масс тела (системы
тел) или центром тяжести (последнее в однородном поле гравитации).
x
2.
Движение центра инерции тела(системы тел)
z
zc
С
rc
1
rC m i ri
m i 1
N
Скорость центра инерции
yc
0
y
1 N
1
drc 1 N
dri 1 N
m i i pi P
c
m i
m i 1
m
dt m i 1
dt m i 1
ri m i
x
xc
P m c
Полный импульс системы материальных точек (тела) равен произведению
массы системы материальных точек (тела) на скорость центра инерции.
Для изменения полного
импульса системы найдено
dP
d m C
d C
F
m
maC
dt
dt
dt
Центр инерции тела (системы тел) движется так же, как двигалась бы
материальная точка с массой m под действием результирующей всех
внешних сил, приложенных к телу (системе тел).
3.
Пример:Топор совершает сложное движение.
Однако в соответствии с теоремой о
движении центра масс, его ц.м. движется так
как двигалась бы материальная точка в поле
силы тяжести, если она имела начальную
скорость направленную под углом к
горизонту.
Пример . В некоторой точке
траектории снаряд разрывается на
множество осколков. Как будет
двигаться их центр масс?
По той же траектории (парабола).
Сколь долго это продолжится?
Пока первый осколок не достигнет земли (добавится внешняя сила
реакции земли).
4.
Пример. На покоящееся тело начинаетдействовать "пара" сил F и F*. Как будет
двигаться тело?
Геометрическая сумма внешних сил равна нулю
ускорение центра масс также равно нулю - он останется
в покое.
Будет ли тело двигаться?
Оно будет вращаться вокруг оси проходящей через
неподвижный центр масс.
Центр тяжести.
В однородном поле тяготения равнодействующая сил тяжести приложена
к центру масс тела (системы тел).
Если тело подвешено за
центр масс, то оно находится в безразличном состоянии равновесия.
5.
ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯПростейшая физика динамики вращения АТТ вокруг неподвижной оси
Угловое ускорение не только
пропорционально приложенной
силе, но зависит также от
радиуса шкива l.
Конкретно:
ε~F l
«плечо»
момент силы
F
Ускорение зависит не только от массы вращающихся тел, но и от их
расстояния до оси вращения, а именно
ε~1/(m r2)
mr2
- момент инерции материальной точки относительно оси.
6.
ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯM
Момент силы (вращающий момент).
Момент импульса.
Рассмотрим движение МТ относительно
произвольной точки (центра) О.
Пока не имеется в виду непременно
O
обращение МТ вокруг центра О.
В частности, движение может быть
плечо силы
прямолинейным.
Определение:
l
r
относительно
точки О
Момент силы относительно точки О равен векторному
произведению радиус-вектора на вектор силы:
M
– момент силы,
Величина момента силы:
M [r F ],
M rF sin = Fl
l – плечо силы относительно точки О.
F
7.
Момент импульса м.т. относительно точки (центра)L r p
L
Момент импульса МТ относительно точки
(О) равен векторному произведению
радиус-вектора на вектор импульса МТ:
O
Плечо
относительно
точки О
l
p
r m
L r p sin
L lp
8.
Закон изменения (сохранения) момента импульсаЗакон изменения момента импульса для МТ
Найдем связь между M
и L для материальной точки.
L [r p]
M
=0
dL d[ r p] dr dp
p r [ m ] [r F ] M
dt
dt
dt
dt
Скорость изменения момента импульса материальной точки равна
моменту сил и определяется уравнениями моментов:
dp
F
dt
dL
M
dt
Смысл введения
M и
L
9.
dLM
dt
M 0
L const
Момент импульса МТ сохраняется, если
момент силы равен 0.
10.
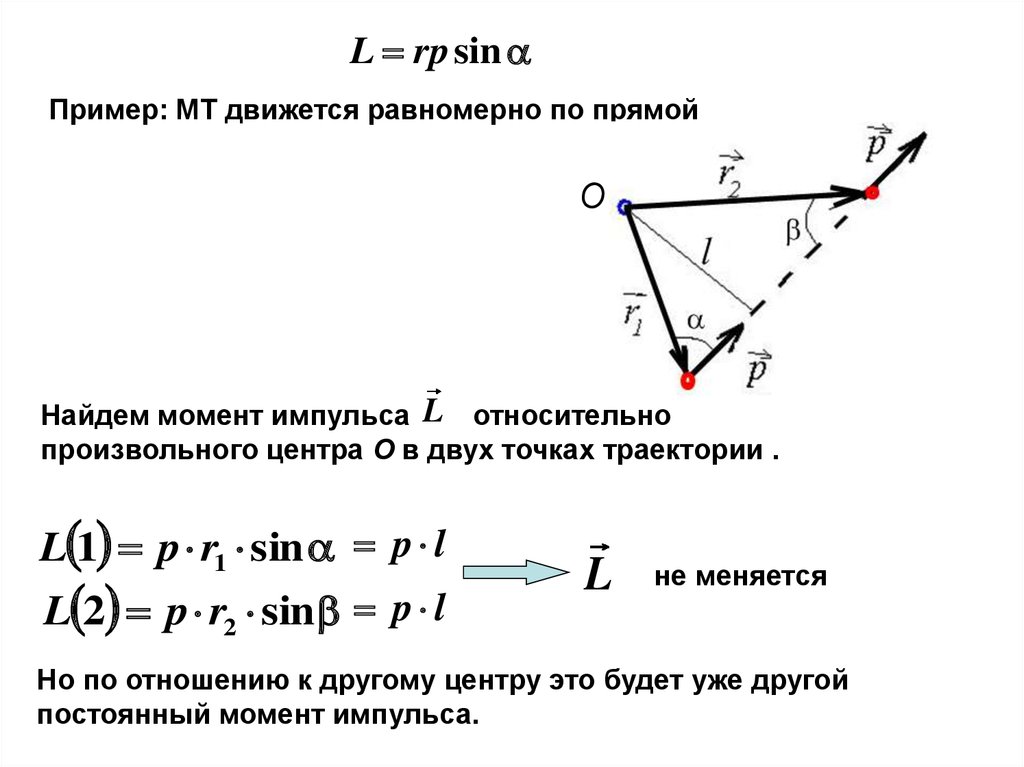
L rp sinПример: МТ движется равномерно по прямой
О
Найдем момент импульса L относительно
произвольного центра О в двух точках траектории .
L 1 p r1 sin p l
L 2 p r2 sin p l
L
не меняется
Но по отношению к другому центру это будет уже другой
постоянный момент импульса.
11.
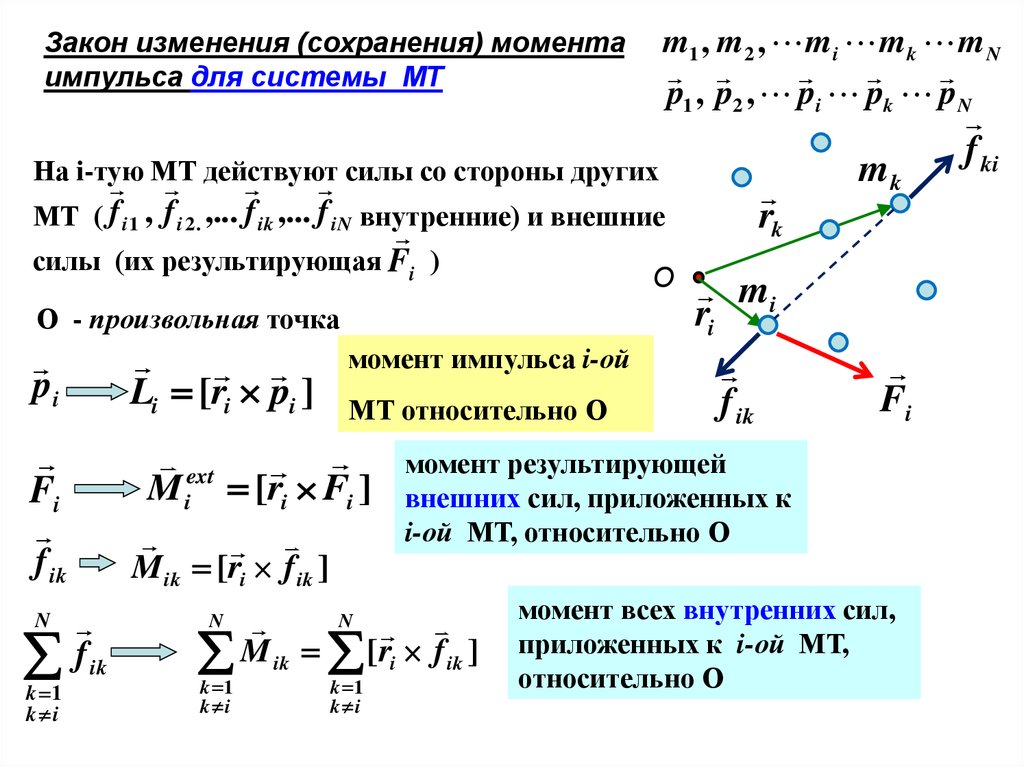
m1 , m2 , mi mk m Np1 , p2 , pi pk pN
Закон изменения (сохранения) момента
импульса для системы МТ
На i-тую
МТ
действуют
силы со стороны других
МТ ( f i 1 , f i 2 . ,... f ik ,... f iN внутренние) и внешние
силы (их результирующая Fi )
О
О - произвольная точка
Li [ri pi ]
pi
Fi
k 1
k i
МТ относительно О
ext
M i [ri Fi ]
f ik
N
момент импульса i-ой
M ik [ri f ik ]
f ik
k 1
k i
k 1
k i
mi
ri
f ik
Fi
момент результирующей
внешних сил, приложенных к
i-ой МТ, относительно О
N
M ik [ri f ik ]
N
rk
mk
момент всех внутренних сил,
приложенных к i-ой МТ,
относительно О
f ki
12.
Закон изменения (сохранения) момента импульса для системы МТДля i-ой МТ
dLi
dt
ext
M ik M i
N
k 1
k i
Просуммируем обе части по i
=0
N
N N
N
dLi
ext
M
M
ik
i
i 1 dt
i 1 k 1
i 1
ext
k i
=L
N
dLi
d
dL
L
i
d
t
d
t
dt
i 1
i 1
M
N
dL ext
M
dt
M ik 0
N
Докажем
N
i 1 k 1
k i
13.
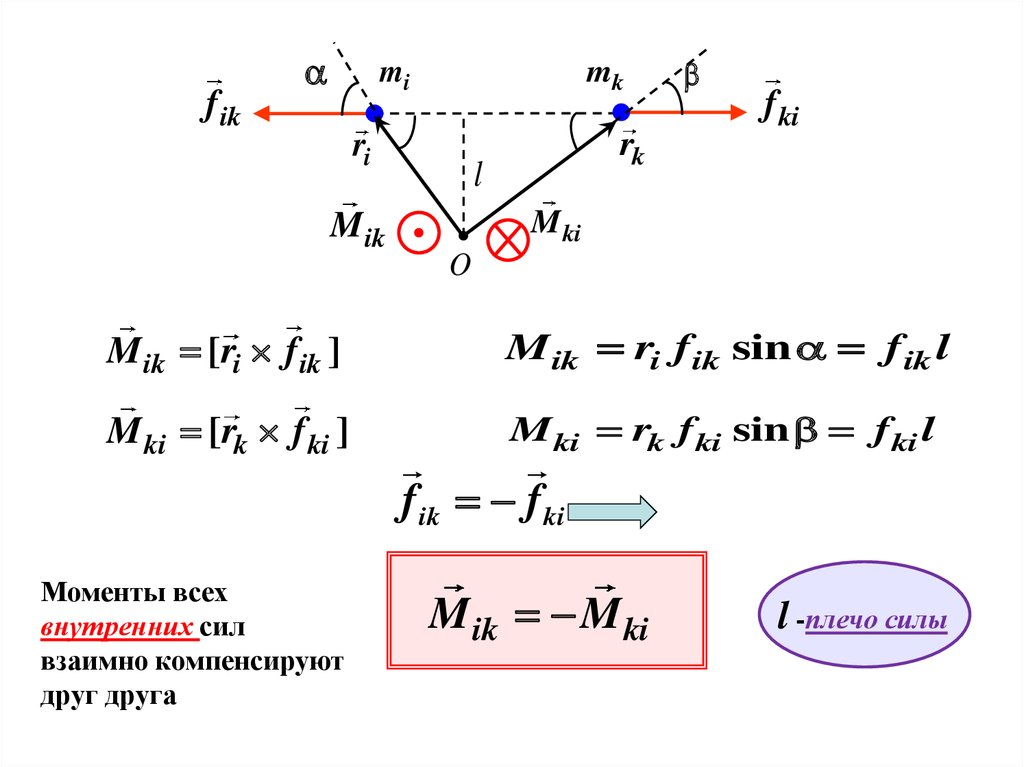
f ikmi
mk
ri
f ki
rk
l
M ki
M ik
O
M ik [ri f ik ]
M ik ri f ik sin f ik l
M ki [rk f ki ]
M ki rk f ki sin f ki l
Моменты всех
внутренних сил
взаимно компенсируют
друг друга
f ik f ki
M ik M ki
l -плечо силы
14.
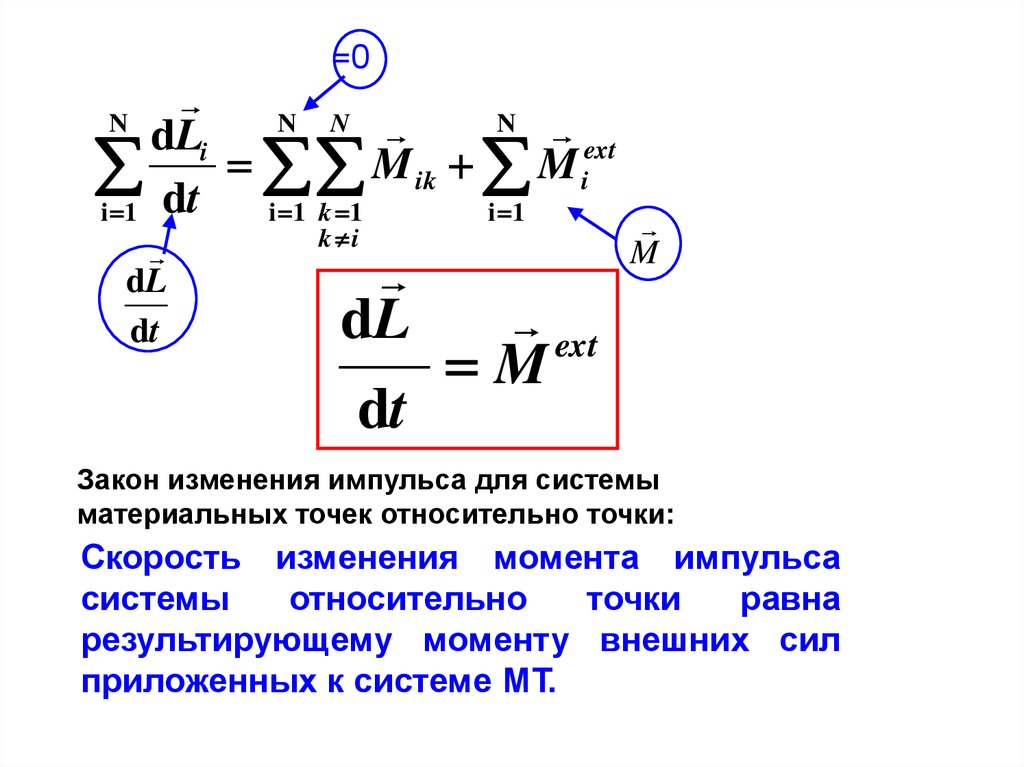
=0N
N N
N
dLi
ext
M
M
ik
i
i 1 dt
i 1 k 1
i 1
dL
dt
k i
dL
dt
M
ext
M
Закон изменения импульса для системы
материальных точек относительно точки:
Скорость изменения момента импульса
системы
относительно
точки
равна
результирующему моменту внешних сил
приложенных к системе МТ.
15.
Еслиext
M 0
, то
dL
0
dt
L const
Закон сохранения момента импульса:
Суммарный момент импульса системы МТ относительно
точки - величина постоянная, если векторная сумма
моментов всех внешних сил относительно точки,
действующих на систему, равна нулю.
16.
Момент импульса относительно неподвижной осиМомент импульса м.т.
относительно точки
Момент импульса м.т. относительно оси
равен проекции вектора L на ось Z
L
z
Lz L cos
L
Lz
O
m
r
z
p
0
LZ L
LZ
17.
zLz
p
p
R
p - проекция вектора p
на плоскость,
перпендикулярную оси
Lz R p
l R
плечо
Lz p l
z
18.
Момент силыотносительно точки
Момент силы относительно оси
равен проекции вектора M на ось Z
M
MZ
z
M
M Z M cos
MZ
Точка приложения силы
O
F
r
z
0
MZ M
19.
zR
Mz
F
F
F - проекция вектора F
на плоскость,
перпендикулярную оси
z
M z R F
l R плечо силы
M z F l
20.
dLdt
ext
M
в проекциях на оси центр, которых
находится в точке О:
dLx
ext
Mx
dt
Mx
ext
0
Lx const;
dLy
dt
My
My
ext
ext
0
Ly const;
Векторное уравнение
Три независимых
уравнения
dLz
ext
Mz
dt
Mz
ext
0
Lz const
21.
Проблемы приполетах…..
M 0 L const 0
L Li L propeller LCarlson 0
i
( LCarlson ) Z ( L propeller ) Z
22.
23.
Момент инерции материальной точки относительнооси, перпендикулярной плоскости её обращения
LZ L
МТ движется по окружности в плоскости,
перпендикулярной оси (z), проходящей через центр
окружности.
R
Момент импульса МТ относительно точки О :
LZ [ R p]
Проекция момента импульса на ось z
m
p
2
mR
R
m
R
Lz Lz Rp sin Rm
2
2
I z mR - момент инерции материальной точки относительно оси z.
Момент инерции материальной точки относительно оси – это величина,
равная произведению массы материальной точки на квадрат расстояния
до оси вращения.
24.
Момент инерции материальной точки относительнооси, перпендикулярной плоскости её обращения
I z mR 2
LZ L
Lz mR 2 I z
R
Lz I z
m
В векторной форме:
Lz I z
p m
p
25.
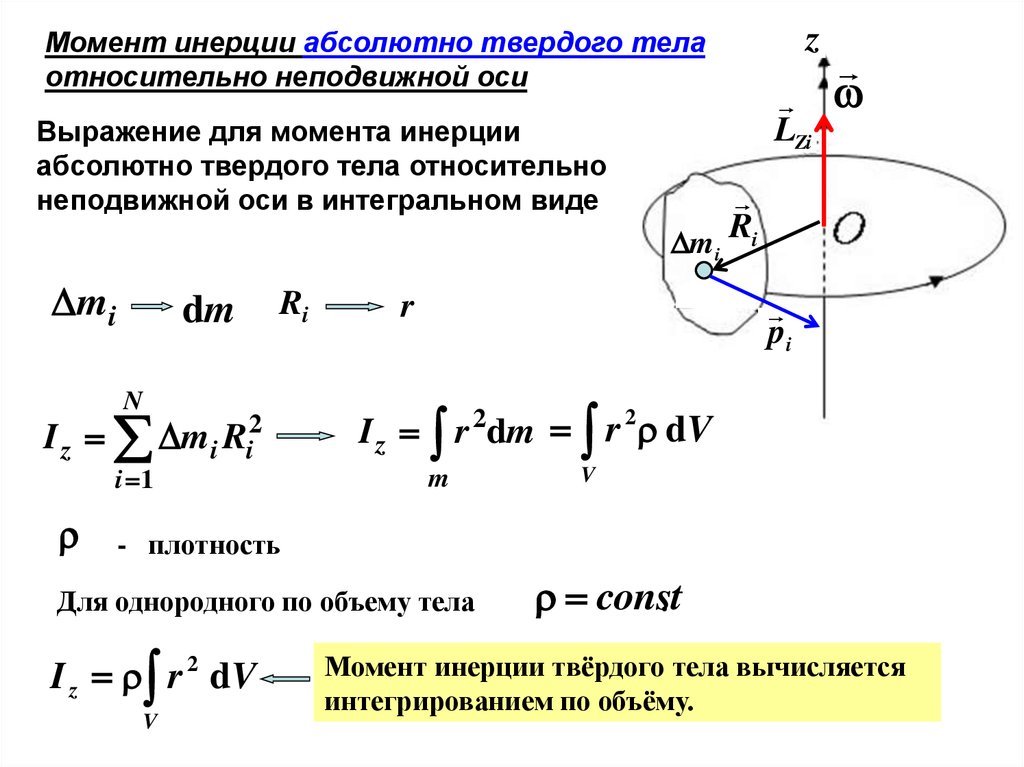
zМомент инерции абсолютно твердого тела
относительно неподвижной оси
Тело как совокупность N материальных точек
mi – масса i -ой МТ,
МТ до оси
Ri – расстояние от i -ой
m i
Момент импульса относительно оси для абсолютно
твердого тела, как системы материальных точек:
N
I z mi Ri2
i 1
LZi
Ri
pi
момент инерции абсолютно твердого тела
относительно оси z
Iz зависит от: 1) массы материальных точек (тела);
2) распределения масс в теле относительно оси (Ri);
3) выбора оси.
26.
Момент инерции абсолютно твердого телаотносительно неподвижной оси
Выражение для момента инерции
абсолютно твердого тела относительно
неподвижной оси в интегральном виде
mi
dm
N
Iz
i 1
Ri
mi Ri2
z
LZi
mi Ri
pi
r
2
I z r 2dm r dV
m
V
- плотность
Для однородного по объему тела
I z r 2 dV
V
const
.
Момент инерции твёрдого тела вычисляется
интегрированием по объёму.
27.
Момент инерции относительно неподвижной осиНе абсолютно твердое тело
Lz I z
Lz
Iz
Момент инерции зависит от формы
тела и может изменяться
Если Mz =0, то Lz= const,
и при изменении момента инерции, угловая скорость будет меняться
I z
I z
Примеры: фигурное катание и т. п.
28.
Основное уравнение динамики вращательного движенияРассмотрим абсолютно твердое тело, вращающееся относительно
неподвижной оси.
Момент импульса тела относительно оси
Lz I z
Под действием внешних сил
Lz
и
dLz
d
Iz
dt
dt
dLz
Mz
dt
d
dt
Mz
Iz
будут меняться.
F
a
m
основное уравнение динамики вращательного движения
29.
Примеры расчета момента инерции абсолютно твердоготела
1. Тонкое кольцо, полый тонкостенный цилиндр
Найдём момент инерции относительно оси
симметрии
I z mi ri2 mi R 2 R 2 mi mR 2
i
i
I z mR 2
i
2. Однородный диск, сплошной цилиндр
Найдём момент инерции относительно оси
симметрии, проходящей через центр масс.
I z r dV
2
dr
r
dV 2 r hdr
V
R
h
R
4
R
3
2
2
h
r
I z r 2 r hdr
0 dr 2 h 4
0
R h V V m
2
mR
Iz
2
2
2R
30.
m1 m2N
Iz
i 1
2
mi Ri
<
I1 ? I 2
31.
Теорема ШтейнераZC
Z
d
Момент
инерции
тела
относительно
произвольной оси Z равен сумме момента
C
инерции этого тела относительно оси,
параллельной данной и проходящей через
центр масс этого тела, и произведения массы
тела на квадрат расстояния между осями
I Z I C md 2
Iz– искомый момент инерции тела относительно оси Z;
IC - момент инерции тела относительно оси , параллельной оси Z и
проходящей через центр масс тела – точку С ;
d – расстояние между осями;
m – масса тела
32.
Момент инерции однородного стержня.ZC
Z
1. Момент инерции стержня относительно
оси ZC, перпендикулярной стержню и
проходящей через его центр (центр масс).
r
C
Pазобьем стержень на элементарные участки
длиной dr.
m
dm dr
l
l 2
1
IC ml 2
12
3 l/2
l 2
r
2
2
r
d
r
2
I c 2 dI C
0
3
0
0
l
2
l
2
d I c r 2 dm r 2 d r
l 3 ml 2
2
24
12
2. Момент инерции относительно оси Z, проходящей
через конец стержня параллельной оси ZC .
Согласно теореме Штейнера
2
2
2
ml
ml
ml
l
I Z IC m
12
4
3
2
2
dr
1 2
I Z ml
3


























 Физика
Физика








