Похожие презентации:
Семинар №12
1. Симплекс – метод.
Семинар 132. Алгоритм симплекс-метода решения ЗЛП
Для того, чтобы решить ЗЛП симплекс методом, необходимо выполнить следующее:1.
Привести задачу к каноническому виду.
2.
Найти начальное опорное решение с «единичным» базисом ( с базисом из
единичных векторов) и коэффициенты разложений векторов условий по базису
опорного решения.
3.
Если опорное решение отсутствует, то задача не имеет решения ввиду
несовместности системы ограничений.
4.
Вычислить оценки разложений векторов условий по базису опорного решения и
заполнить симплекс-таблицу.
5.
Если выполняется признак единственности оптимального решения (Следствие№3),
то решение задачи заканчивается.
6.
Если выполняется признак существования бесконечного множества оптимальных
решений (Следствие№4), то путем простого перебора находят все оптимальные
решения.
7.
Если выполняется признак отсутствия оптимального решения ввиду
неограниченности целевой функции (Следствие№5) , то задача не имеет решения
ввиду неограниченности целевой функции.
8.
Если пункты 5-7 алгоритма не выполняются, то находят новое опорное решение с
использованием условий следствие№1 и возвращаются к п.4.
3. Пример
Решить З.Л.П. симплекс - методомZ ( X ) x1 4 x 2 x3 11 min
x1 2 x 2 x3 4,
3 x1 x 2 2 x3 9,
2 x 3 x x 6,
3
2
1
___
x j 0, j 1,3
Z (min) = -3, X(2,3,0)
4. Решить З.Л.П. симплекс - методом
Z ( X ) x1 4 x2 x3 11 minx1 2 x2 x3 4,
3x1 x2 2 x3 9, x4
2 x 3x x 6, x
2
3
5
1
___
x j 0, j 1,3
Z ( X ) x1 4 x2 x3 0 x4 0 x5 11 min
x1 2 x2 x3 4,
3x1 x2 2 x3 x4 9,
2 x 3x x x 6
2
3
5
1
___
x j 0, j 1,3
Из таблицы видно, что при
X(2;3;0)
minZ(X) = –2 – 4·3 –0 + 11 =
=–3
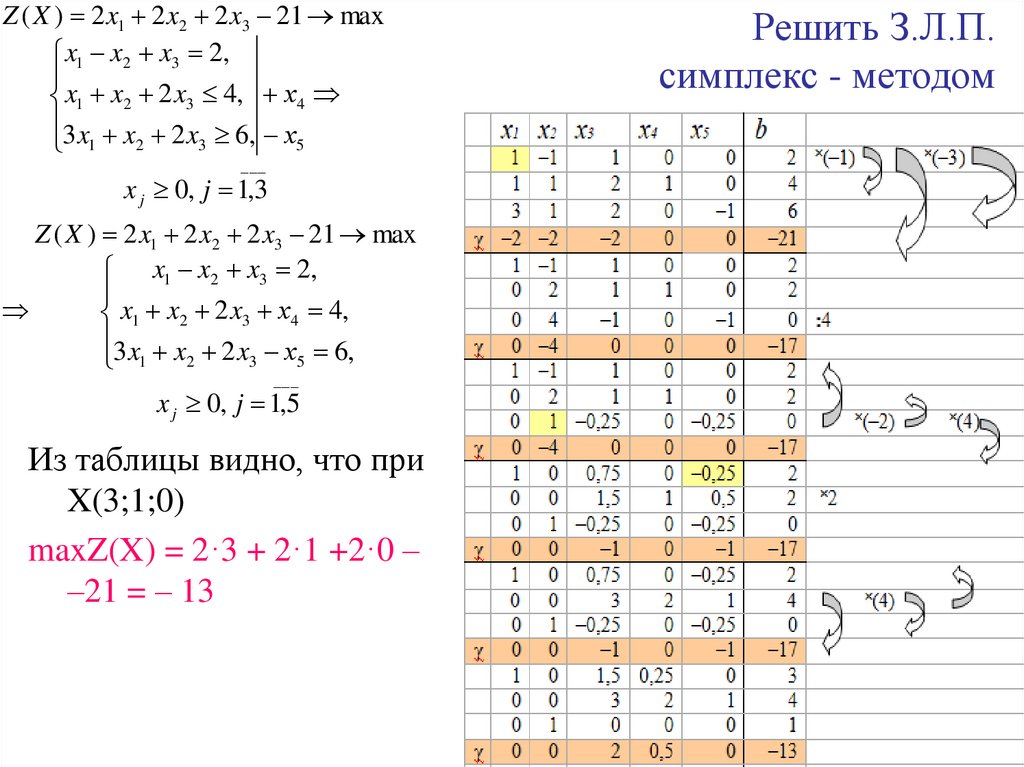
5. Пример
Решить З.Л.П. симплекс - методомZ ( X ) 2 x1 2 x2 2 x3 21 max
x1 x2 x3 2,
x1 x2 2 x3 4,
3 x x 2 x 6,
2
3
1
___
x j 0, j 1,3
Ответ:
Z (max) = –13, при X( 3,1, 0)
6. Решить З.Л.П. симплекс - методом
Z ( X ) 2 x1 2 x2 2 x3 21 maxx1 x2 x3 2,
x1 x2 2 x3 4, х4
3x x 2 x 6, х
3
5
1 2
___
x j 0, j 1,3
Z ( X ) 2 x1 2 x2 2 x3 21 max
x1 x2 x3 2,
x1 x2 2 x3 х4 4,
3 x x 2 x х 6,
3
5
1 2
___
x j 0, j 1,5
Из таблицы видно, что при
X(3;1;0)
maxZ(X) = 2·3 + 2·1 +2·0 –
–21 = – 13
Решить З.Л.П.
симплекс - методом
7. Симплекс-метод
Нет решения8. Решить З.Л.П.
Z x 5 x1 2 x2 3x3 min3x1 2 x2 3x3 2,
3x1 4 x2 5 x3 10,
x 4 x x 1,
2
3
1
___
x j 0, j 1,3
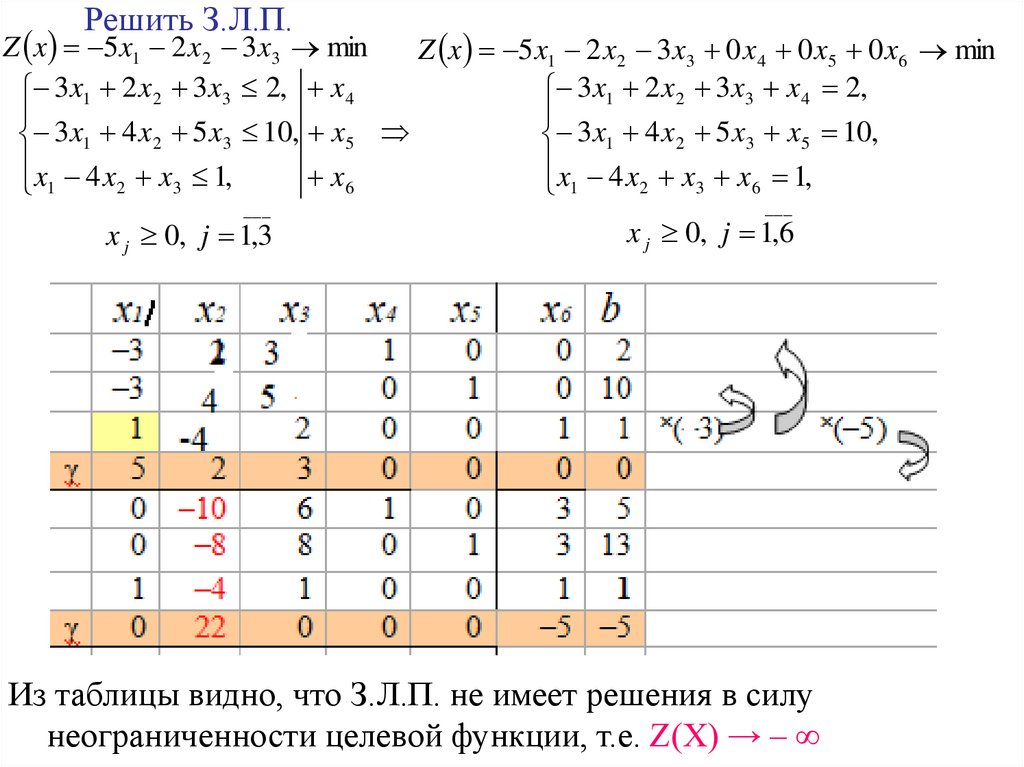
9. Решить З.Л.П.
Z x 5 x1 2 x 2 3x3 minZ x 5 x1 2 x 2 3x3 0 x 4 0 x5 0 x6 min
3x1 2 x 2 3x3 2, x 4
3x1 2 x 2 3x3 x 4 2,
3x1 4 x 2 5 x3 10, x5
3x1 4 x 2 5 x3 x5 10,
x 4 x x 1,
x 4 x x x 1,
x
2
3
6
2
3
6
1
1
___
x j 0, j 1,3
___
x j 0, j 1,6
Из таблицы видно, что З.Л.П. не имеет решения в силу
неограниченности целевой функции, т.е. Z(X) → – ∞
10. Решить З.Л.П.
Z x x1 2 x2 2 x3 max2 x1 3x2 x3 8,
x1 2 x2 2 x3 4,
3 x 2 x x 12,
2
3
1
___
x j 0, j 1,3
11. Решить З.Л.П.
Z x x1 2 x 2 2 x3 max2 x1 3x 2 x3 8, x 4
x1 2 x 2 2 x3 4, x5
3x 2 x x 12,
2
3
1
___
x j 0, j 1,3
Z x x1 2 x 2 2 x3 0 x 4 0 x5 max
2 x1 3x 2 x3 x 4 8, Из таблицы видно, что З.Л.П.
не имеет решения в силу
x1 2 x 2 2 x3 x5 4,
неограниченности целевой
3x 2 x x 12,
2
3
1
функции, т.е. Z(X) → + ∞
___
x j 0, j 1,5
12. Решить З.Л.П.
Z x 2 x1 6 x2 x3 x4 max4 x1 5 x2 2 x3 x4 2,
5 x1 4 x2 x3 x4 1,
___
x j 0, j 1,4
13. Решить З.Л.П.
Z x 2 x1 6 x2 x3 x4 max4 x1 5 x2 2 x3 x4 2,
5 x1 4 x2 x3 x4 1,
___
x j 0, j 1,4
Из таблицы видно, что З.Л.П. не имеет
решения в силу несовместности системы.
Ответ: нет решений
14. Решить З.Л.П.
Z x x1 2 x2 4 x3 x4 minx1 2 x2 x3 x4 2,
x1 x2 2 x3 x4 8,
___
x j 0, j 1,4
15. Решить З.Л.П.
Z x x1 2 x2 4 x3 x4 minx1 2 x2 x3 x4 2,
x1 x2 2 x3 x4 8,
___
x j 0, j 1,4
Из таблицы видно, что З.Л.П. не имеет решения в
силу несовместности системы
Ответ: нет решений






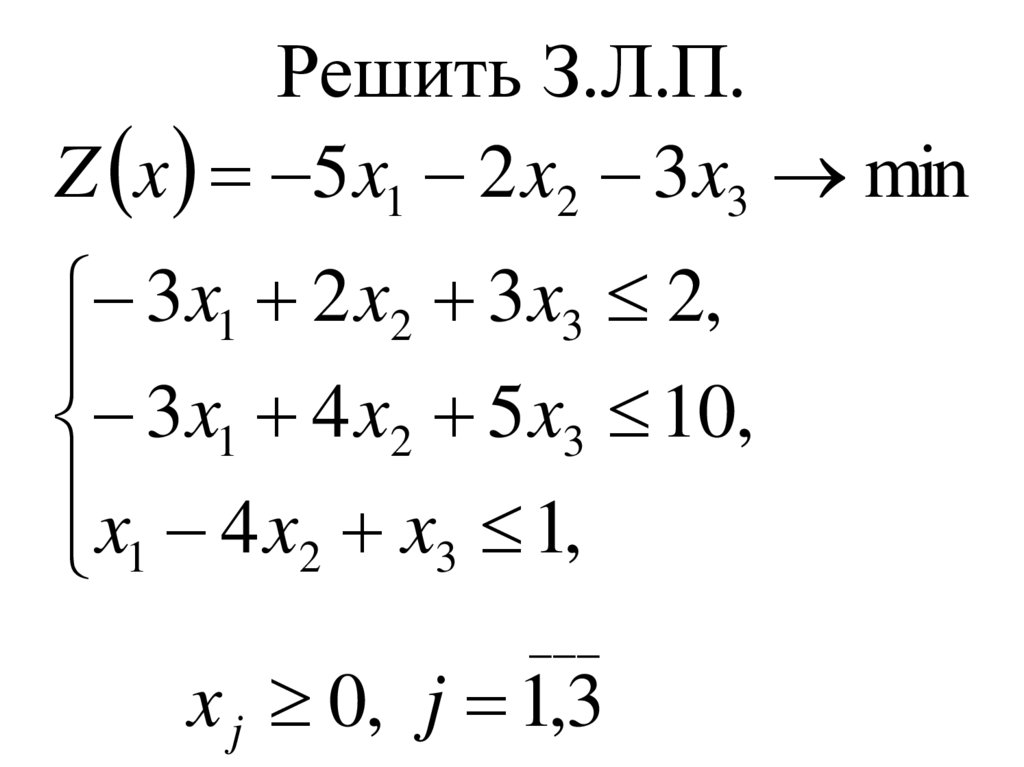
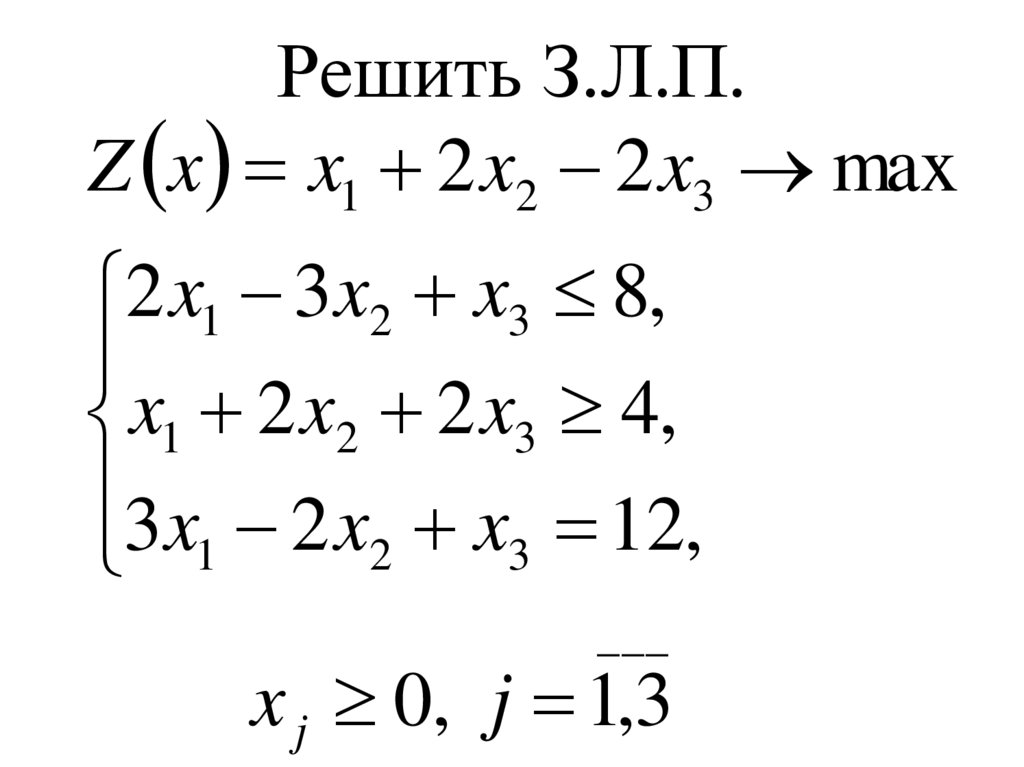

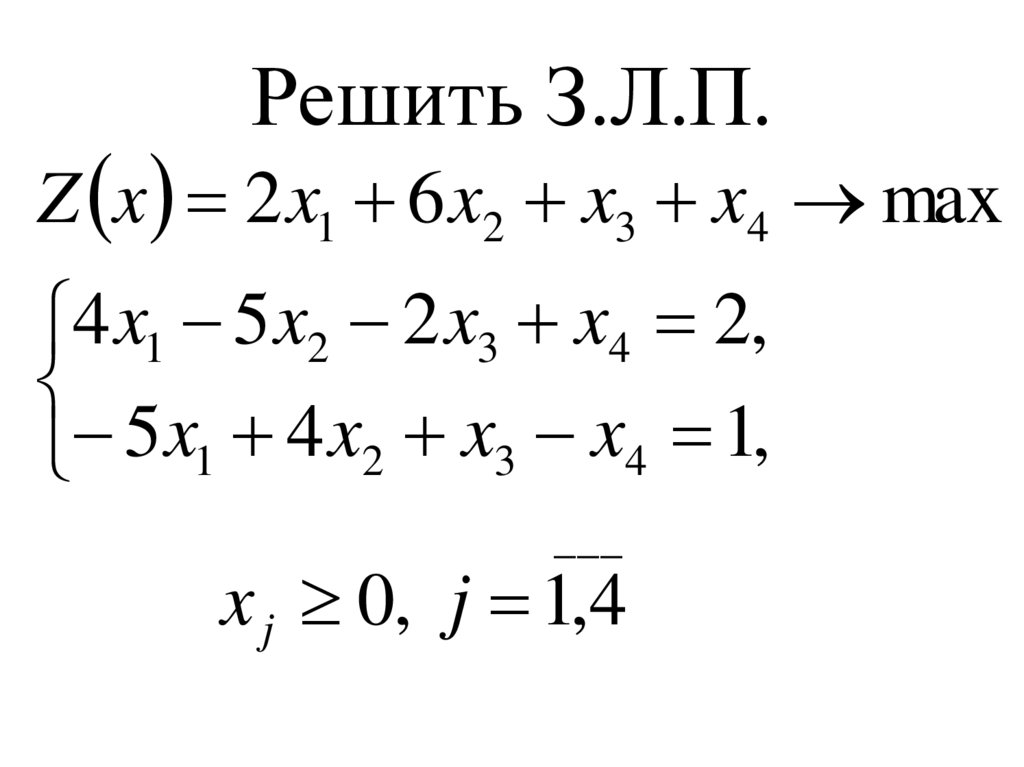

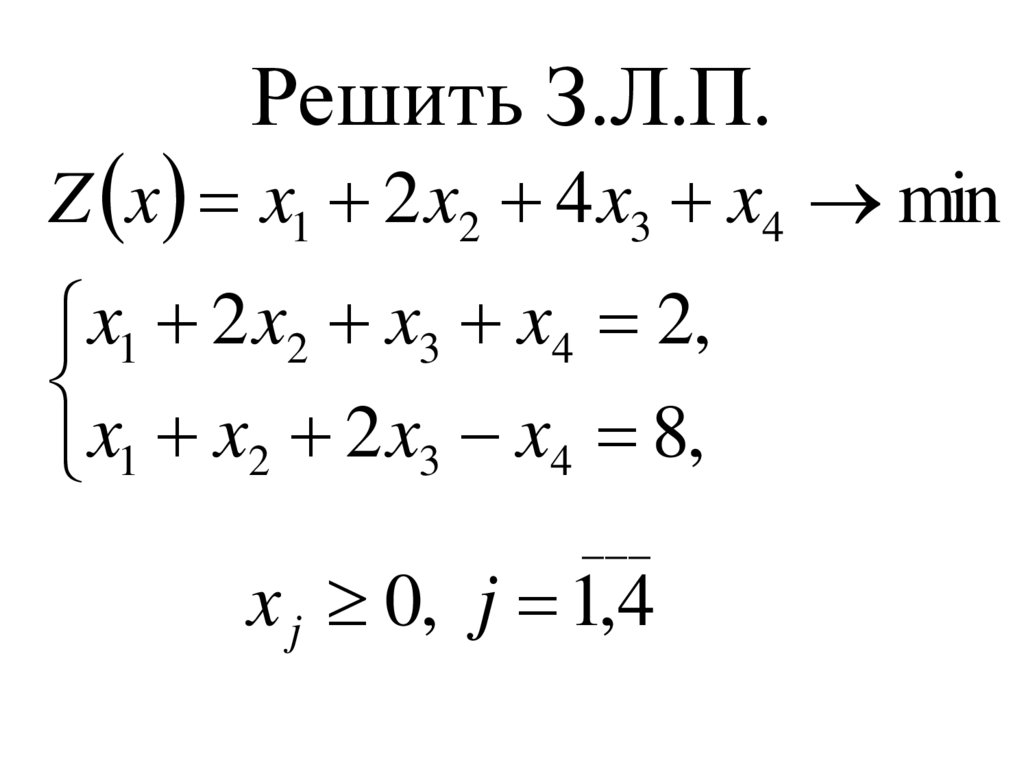

 Математика
Математика








