Похожие презентации:
крутая
1.
Квадратныеуравнения
2.
Цели:Цель нашего проекта - понять систематизация знаний по
теме «Квадратные уравнения» и развитие интереса к
предмету запомнить определение квадратного
уравнения, типы, методы решения.
Задачи:
1.Рассказать определение и историю квадратных
уравнений.
2.Показать способ решения квадратных уравнений.
3.
Определение квадратногоуравнения
Квадратным уравнением
называется уравнение вида
ax bx c 0,
2
где коэффициенты a,b,c-любые
действительные числа, причем
a 0.
4.
Определение корня• Корнем квадратного уравнения
ax bx c 0
2
называют такое значение переменной х,
при котором квадратный трехчлен
2
ax bx c обращается к нулю;
5.
Квадратныеуравнения
умели решать
около 2000 лет
до н. э.
вавилоняне.
6.
Интересные способырешения квадратных
уравнений встречаются в
трудах индийского
ученого Баудхояма..
→
7.
• Вавилонские математикипримерно с IV века до н.э. и
китайские математики
примерно со II века до н.э.
использовали метод
дополнения квадрата для
решения уравнений с
положительными корнями.
Около 300 года до н.э. Эвклид
придумал более общий
геометрический метод
решения..
8.
Применение квадратныхуравнений
-решение рациональных уравнений;
-решение иррациональных уравнений;
-решение задач;
-разложение квадратного трехчлена на
множители;
-сокращение дробей.
9.
Полные квадратныеуравнения
• полные
• пример:
a) b≠0
2x2-5x+3=0
б) c≠0
10x2+6x-9=0
10.
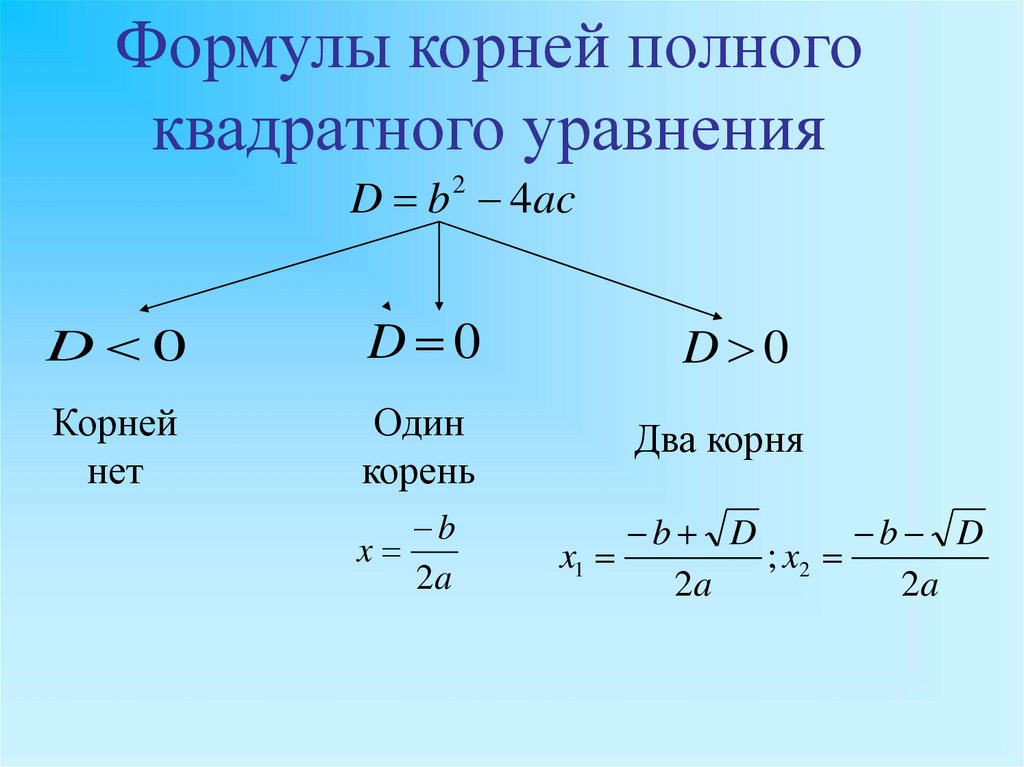
Формулы корней полногоквадратного уравнения
D b 2 4ac
D 0
D 0
D 0
Корней
нет
Один
корень
Два корня
b
x
2a
b D
b D
x1
; x2
2a
2a
11.
Теорема Виетаx1 , x2 - корни квадратного уравнения
b
x1 x2
a
c
x1 x2
a
a 1
x1 x2 b; x1 x2 c
12.
1.Найдите корни квадратного уравнения, неиспользуя формулы корней:
а ) x 2 5 x 6 0;
x1 2; x2 3
б ) x 3 x 4 0;
x1 4; x2 1
в ) x 2 5 x 10 0.
Корней нет
2
13.
Решение квадратных уравненийспособом переброски.
Рассмотрим квадратное уравнение
ах2 + bх + с = 0, а ≠ 0.
Умножая обе его части на а, получаем уравнение
а2 х2 + а bх + ас = 0.
Пусть ах = у, откуда х = у/а ; тогда приходим к уравнению
у2 + by + ас = 0,
Решим уравнение 2х2 – 11х + 15 = 0.
Решение. «Перебросим» коэффициент 2 к свободному члену, в результате
получим уравнение
у2 – 11y +30 = 0.
Согласно теореме Виета
Ответ: 2,5;3.
14.
Неполные квадратныеуравнения
• неполные
a) b=0
• пример:
a) 3x2-8=0
б) c=0
б) x2+4x=0
в) b=0; c=0
в) 5x2=0
15.
Данные уравнения разбейте наполные и неполные:
a)9х2=0;
б)3x+ x2+1=0;
в)2x2-32=0;
г) x2+4x=0;
д)2х2+5х-7=0;
е)12-х2+3х=0.
16.
полные:б) 3х+х2+1=0;
д)2х2+5х-7=0;
неполные:
а) 9х2= 0;
в) 2х2-32=0;
г) х2+4х=0.
е)12-х2+3х=0.
















 Математика
Математика