Design and Optimization of Bolted and Pinned Bracket Joints (1)

1.

Design and Optimization
Bolted and Pinned
Bracket Joints
Focus:
Shear stress • Bearing stress • Failure modes • Safety factor
Optimization

2.

Problem statement and
Design approach
Problem Statement
Design a bracket joint that safely carries a
transverse load while minimizing weight
and maintaining manufacturability.
Approach
Apply stress theory (shear & bearing)
Identify governing failure modes
Perform parameter studies using plots
Select optimal design based on safety
factor
Validate concept with finite element
analysis

3.

Considered types of
Joints
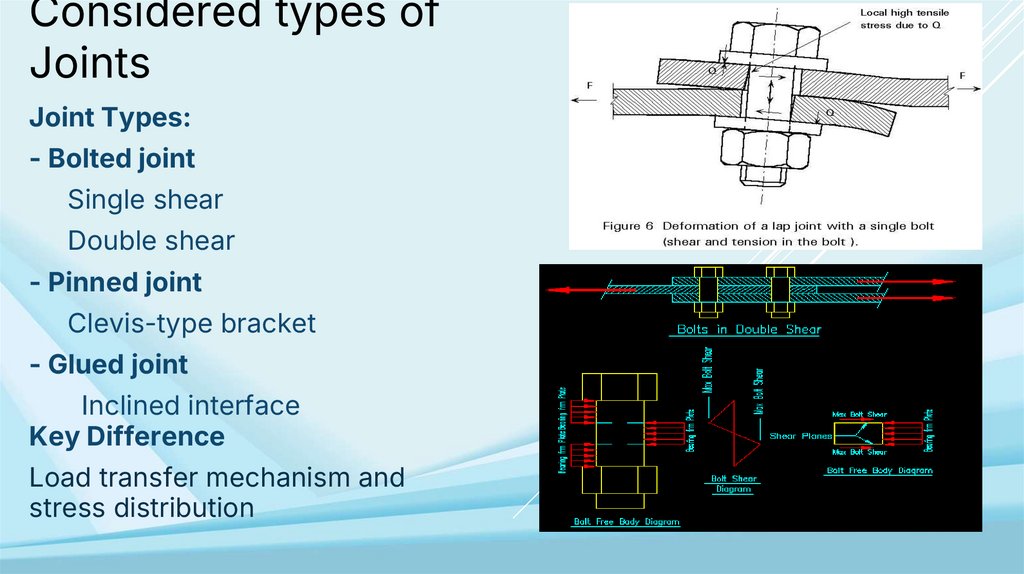
Joint Types:
- Bolted joint
Single shear
Double shear
- Pinned joint
Clevis-type bracket
- Glued joint
Inclined interface
Key Difference
Load transfer mechanism and
stress distribution

4.

Failure modes in Joint
Design
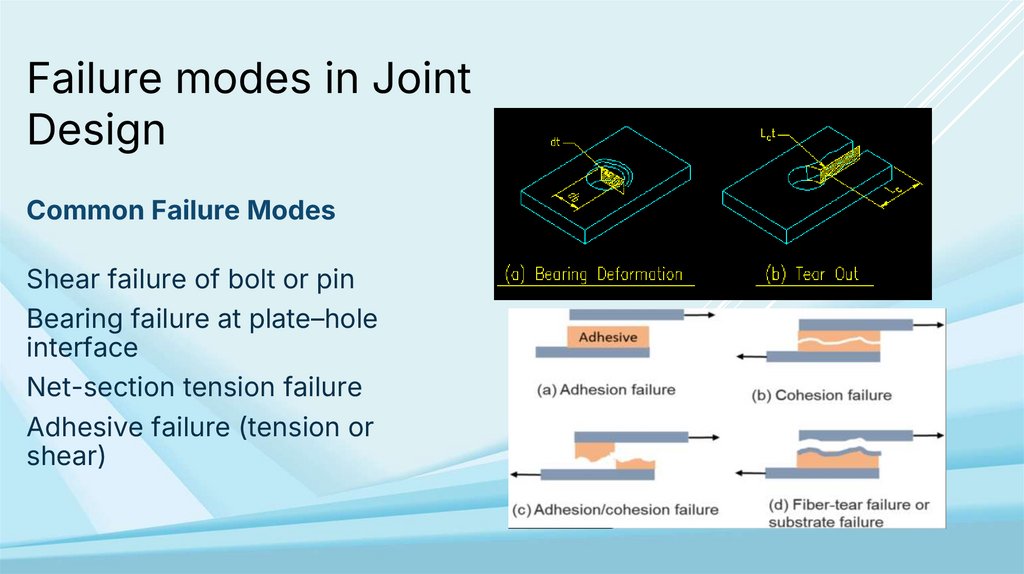
Common Failure Modes
Shear failure of bolt or pin
Bearing failure at plate–hole
interface
Net-section tension failure
Adhesive failure (tension or
shear)

5.

Key Theory from
Solid Mechanics
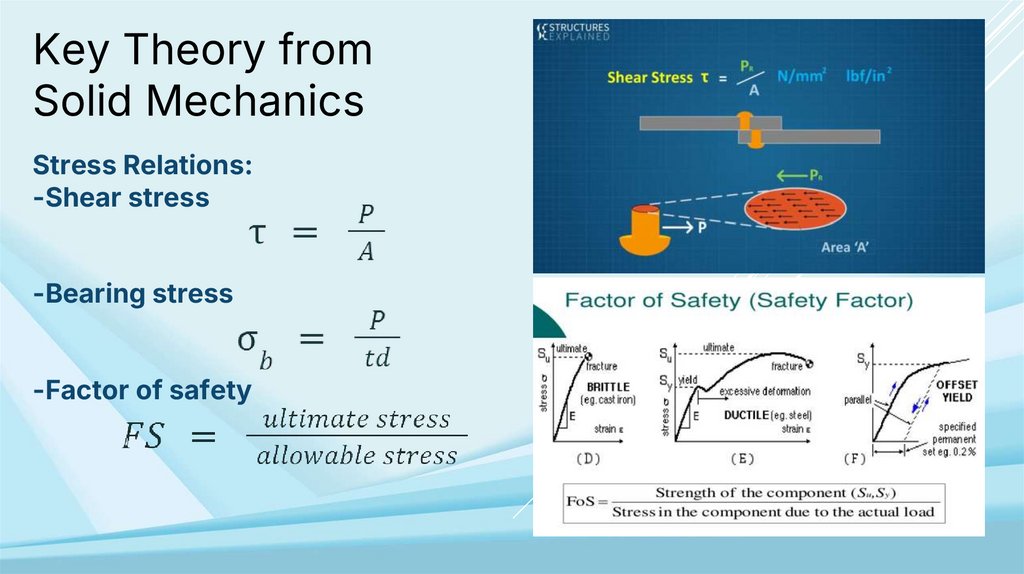
Stress Relations:
-Shear stress
-Bearing stress
-Factor of safety

6.

Bracket concept
and Load path
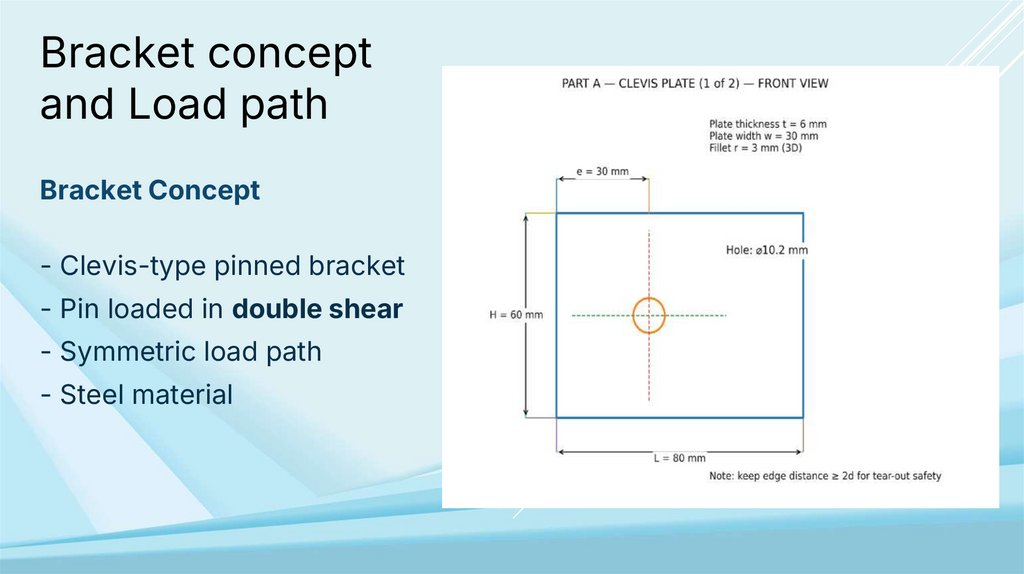
Bracket Concept
- Clevis-type pinned bracket
- Pin loaded in double shear
- Symmetric load path
- Steel material

7.

Analytical design
Assumptions
Design Inputs
Applied load: 10 kN
Allowable shear stress (steel): 100 MPa
Allowable bearing stress (steel): 250
MPa
Target safety factor: FS ≥ 3

8.

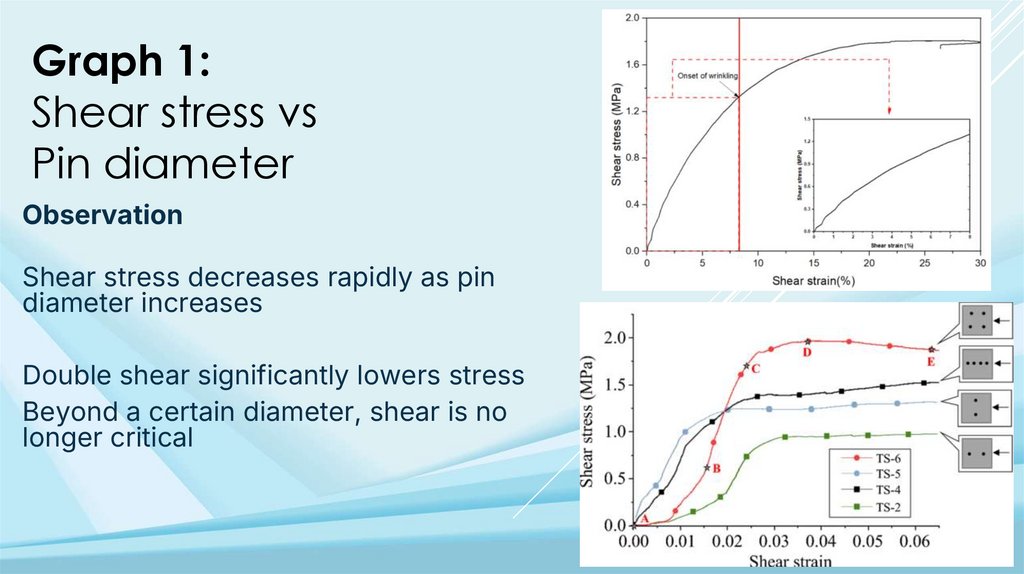
Graph 1:
Shear stress vs
Pin diameter
Observation
Shear stress decreases rapidly as pin
diameter increases
Double shear significantly lowers stress
Beyond a certain diameter, shear is no
longer critical

9.

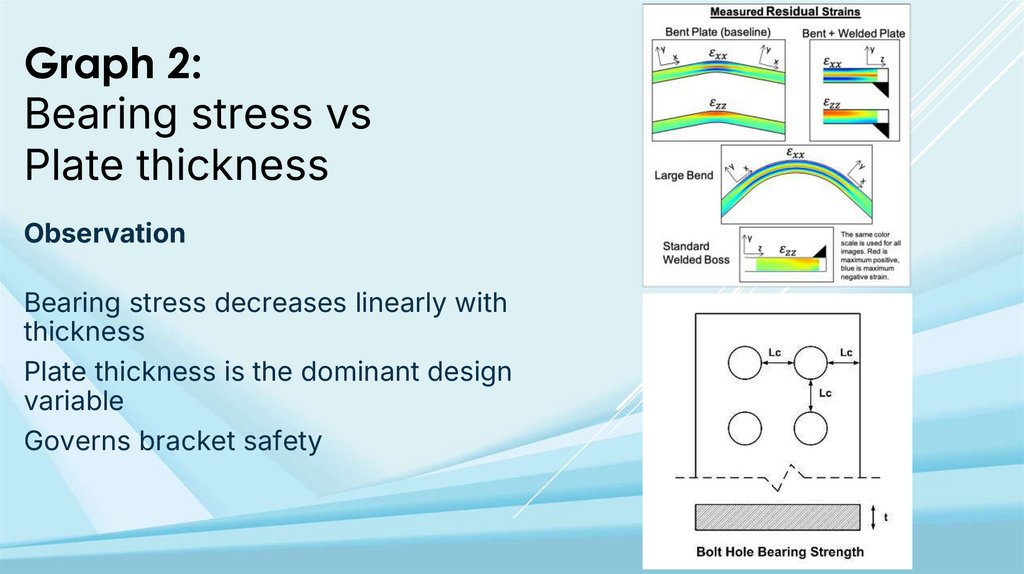
Graph 2:
Bearing stress vs
Plate thickness
Observation
Bearing stress decreases linearly with
thickness
Plate thickness is the dominant design
variable
Governs bracket safety

10.

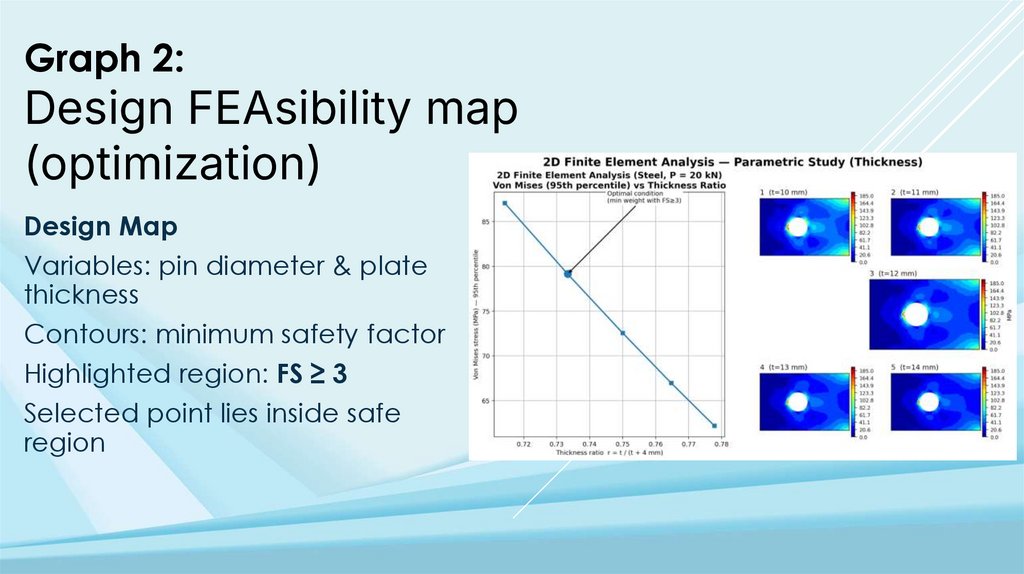
Graph 2:
Design FEAsibility map
(optimization)
Design Map
Variables: pin diameter & plate
thickness
Contours: minimum safety factor
Highlighted region: FS ≥ 3
Selected point lies inside safe
region

11.

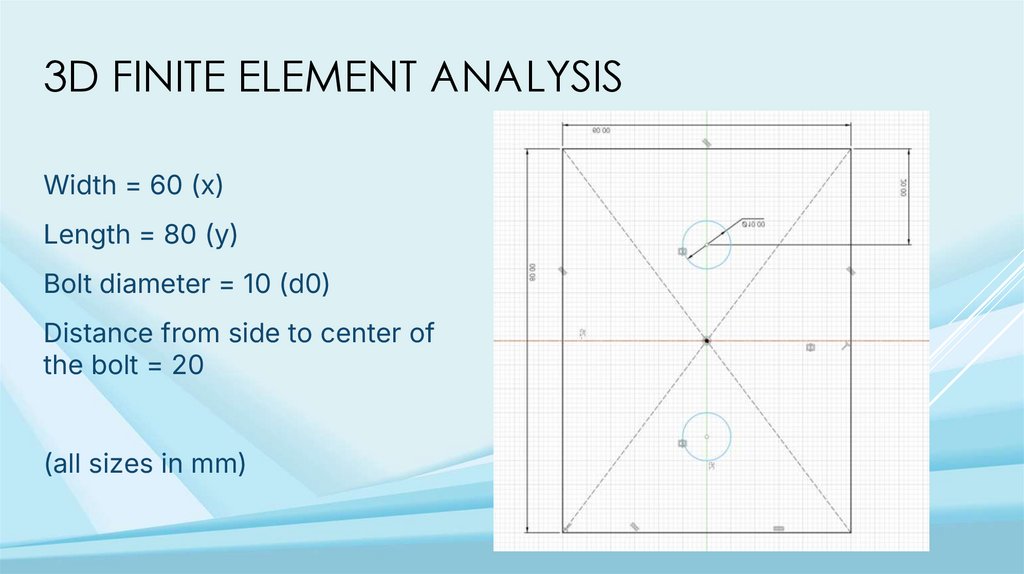
3D FINITE ELEMENT ANALYSIS
Width = 60 (x)
Length = 80 (y)
Bolt diameter = 10 (d0)
Distance from side to center of
the bolt = 20
(all sizes in mm)

12.

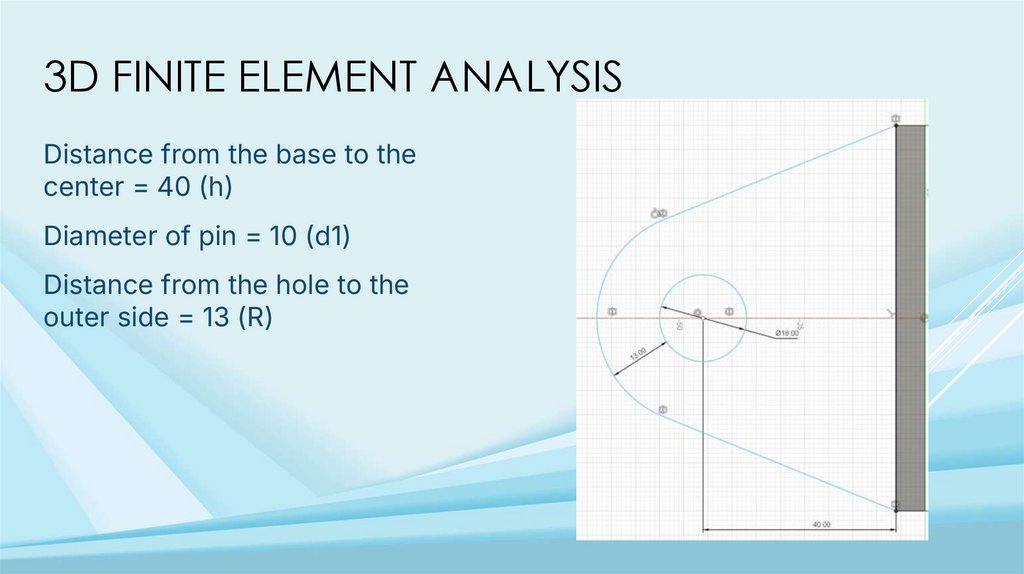
3D FINITE ELEMENT ANALYSIS
Distance from the base to the
center = 40 (h)
Diameter of pin = 10 (d1)
Distance from the hole to the
outer side = 13 (R)

13.

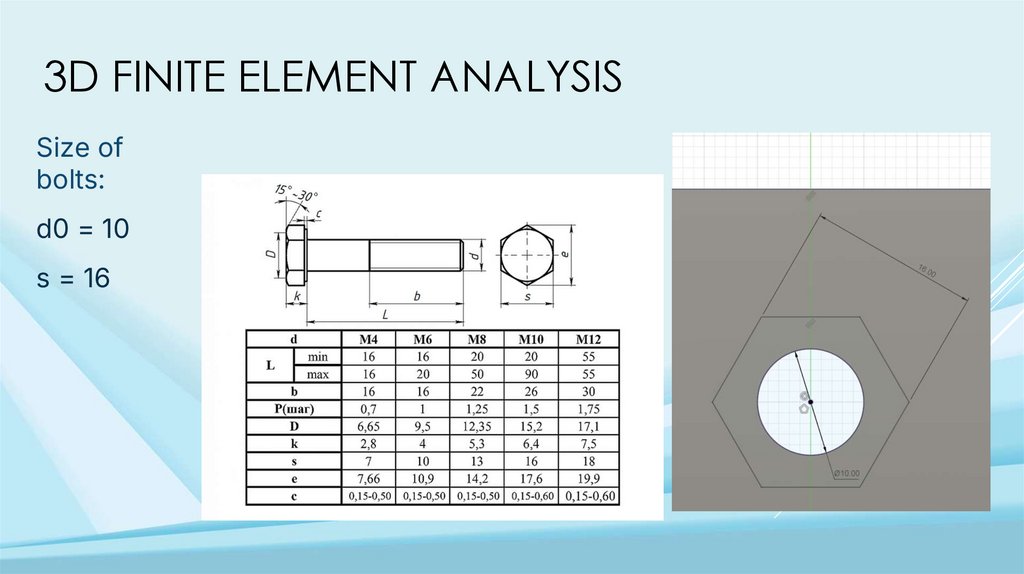
3D FINITE ELEMENT ANALYSIS
Size of
bolts:
d0 = 10
s = 16

14.

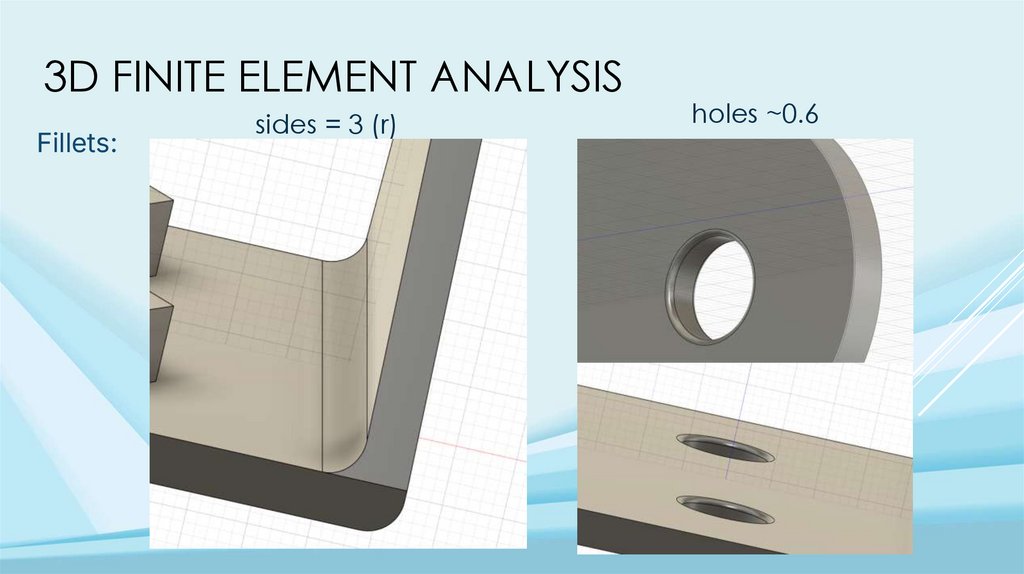
3D FINITE ELEMENT ANALYSIS
Fillets:
sides = 3 (r)
holes ~0.6

15.

3D FINITE ELEMENT ANALYSIS
Preparing for simulation
Load = 20 kN

16.

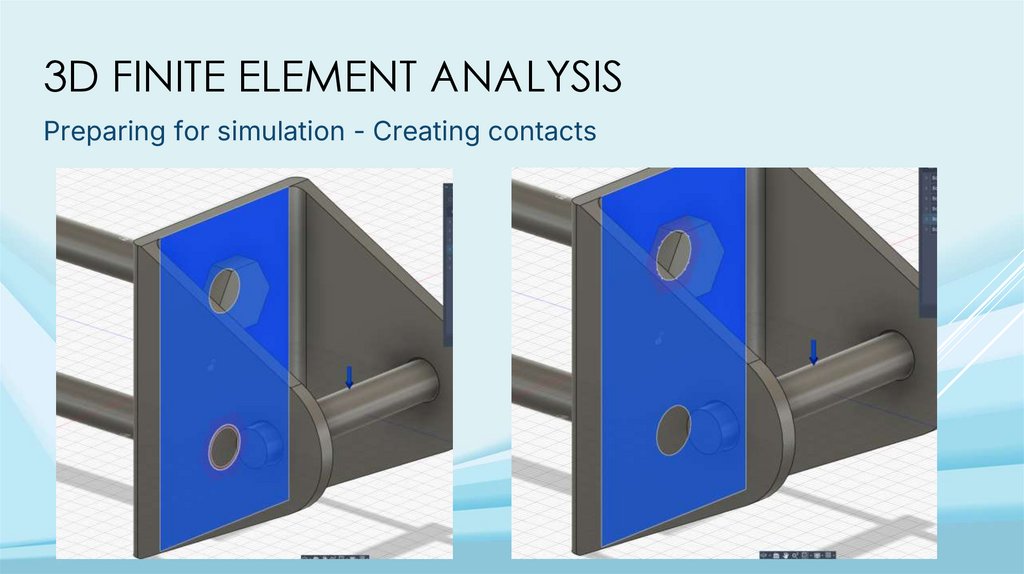
3D FINITE ELEMENT ANALYSIS
Preparing for simulation - Creating contacts

17.

3D FINITE ELEMENT ANALYSIS
Preparing for simulation - Creating contacts

18.

3D FINITE ELEMENT ANALYSIS
Preparing for simulation - Creating contacts

19.

3D FINITE ELEMENT ANALYSIS
Preparing for simulation - Creating mesh

20.

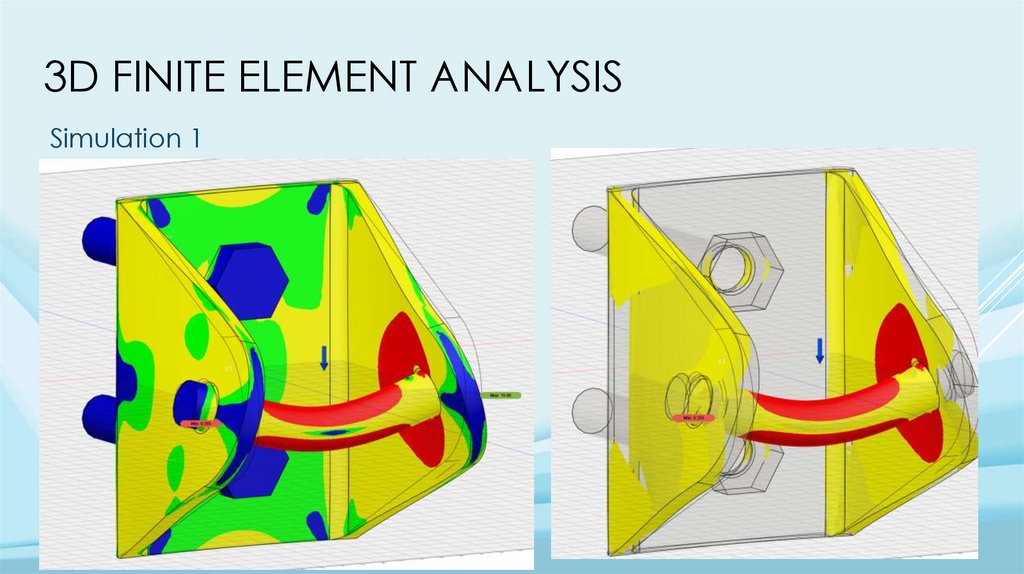
3D FINITE ELEMENT ANALYSIS
Simulation 1

21.

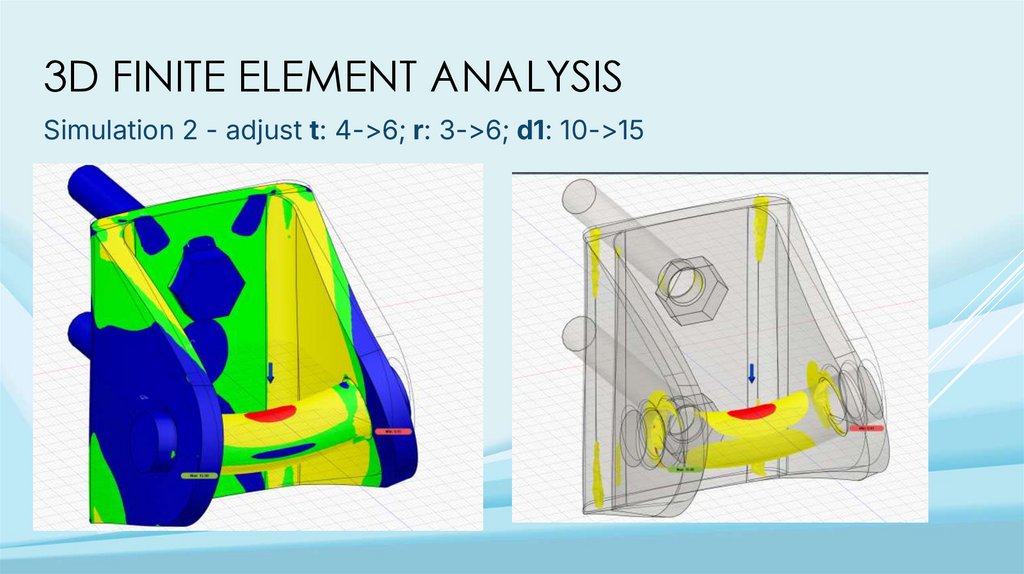
3D FINITE ELEMENT ANALYSIS
Simulation 2 - adjust t: 4->6; r: 3->6; d1: 10->15

22.

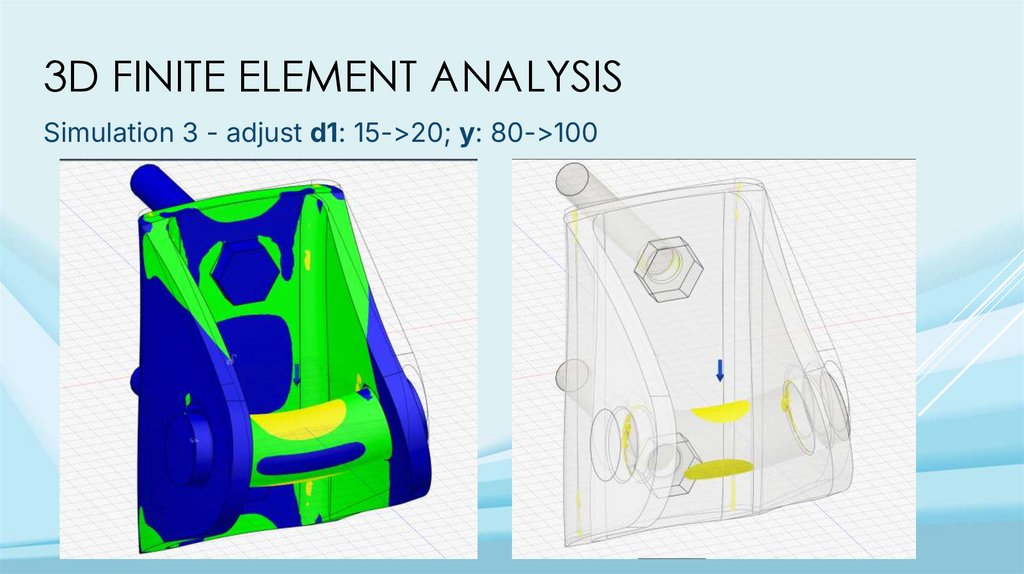
3D FINITE ELEMENT ANALYSIS
Simulation 3 - adjust d1: 15->20; y: 80->100

23.

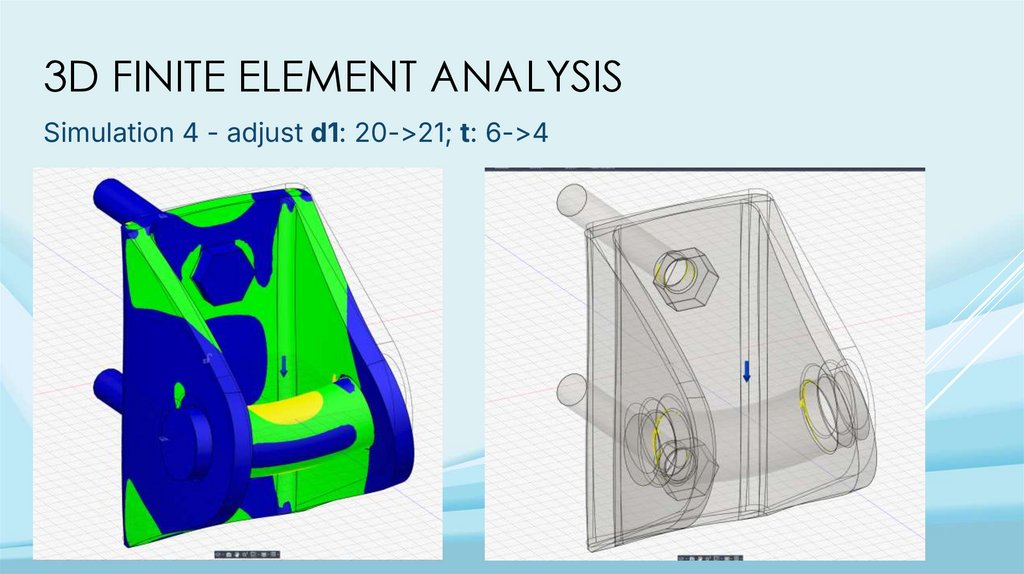
3D FINITE ELEMENT ANALYSIS
Simulation 4 - adjust d1: 20->21; t: 6->4

24.

3D FINITE ELEMENT ANALYSIS
In the classical standard, there are no pins with a diameter of 21 mm

25.

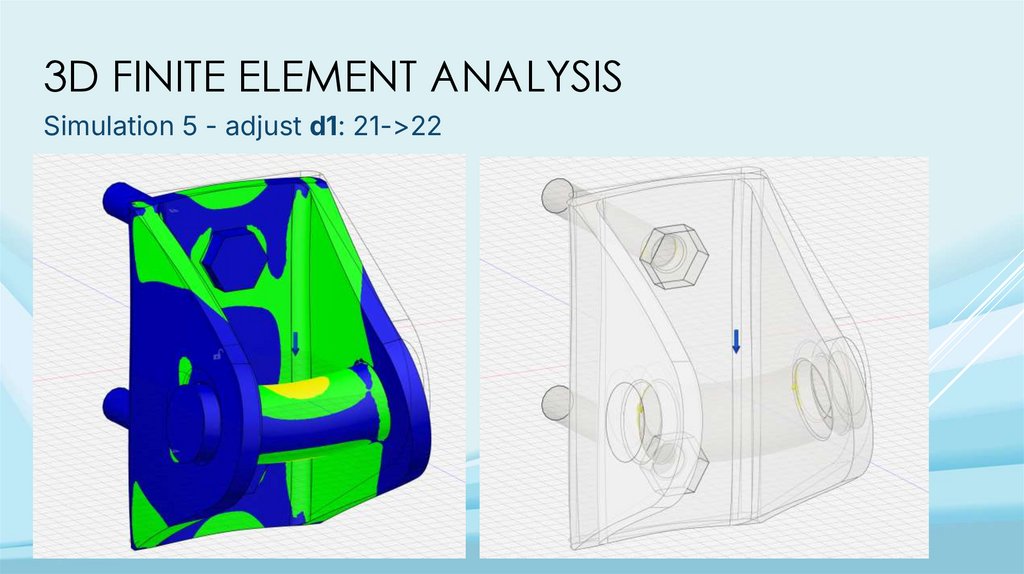
3D FINITE ELEMENT ANALYSIS
Simulation 5 - adjust d1: 21->22

26.

3D FINITE ELEMENT ANALYSIS
Final results iterative approach,
where each modification was
based on stress distribution
observed in the “Safety factor”
Base: x=60, y=100, d0=10, t=6
Sides: h=40, d1=22, r=4, R=13