Axles and shafts

1. AXLES AND SHAFTS

2. AXLES AND SHAFTS

Links intended to carry rotating elements
(pulleys, sprockets, pinions, gears, halfcouplings, etc.) are called as axles or shafts.

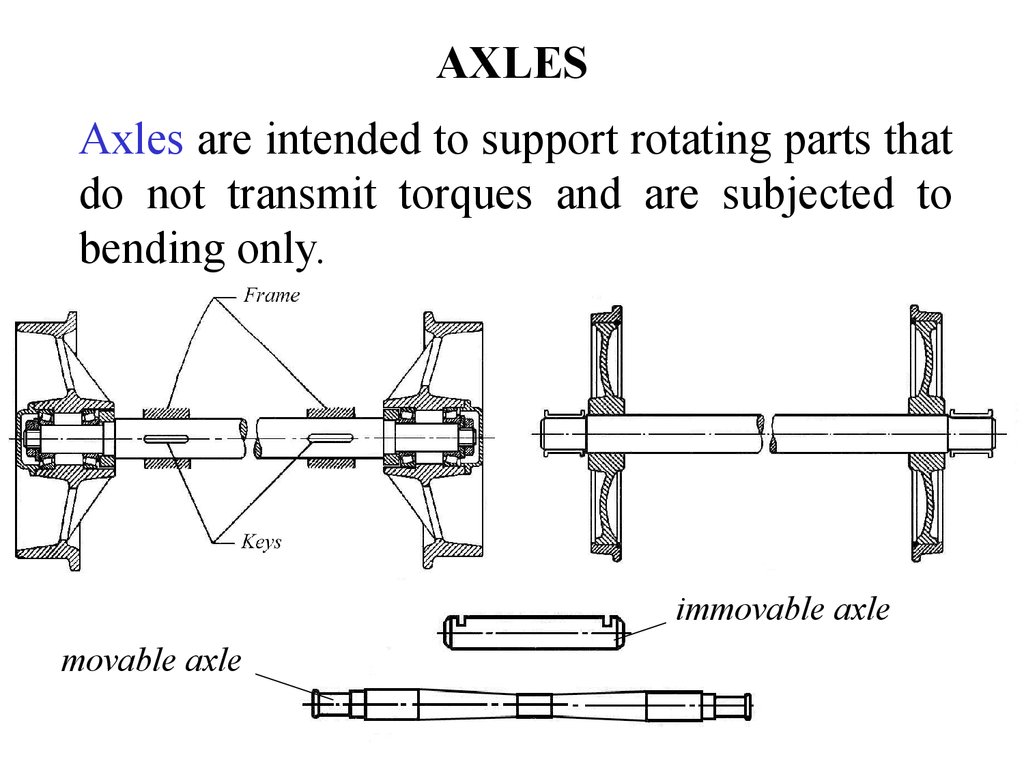
3. AXLES

Axles are intended to support rotating parts that
do not transmit torques and are subjected to
bending only.
immovable axle
movable axle

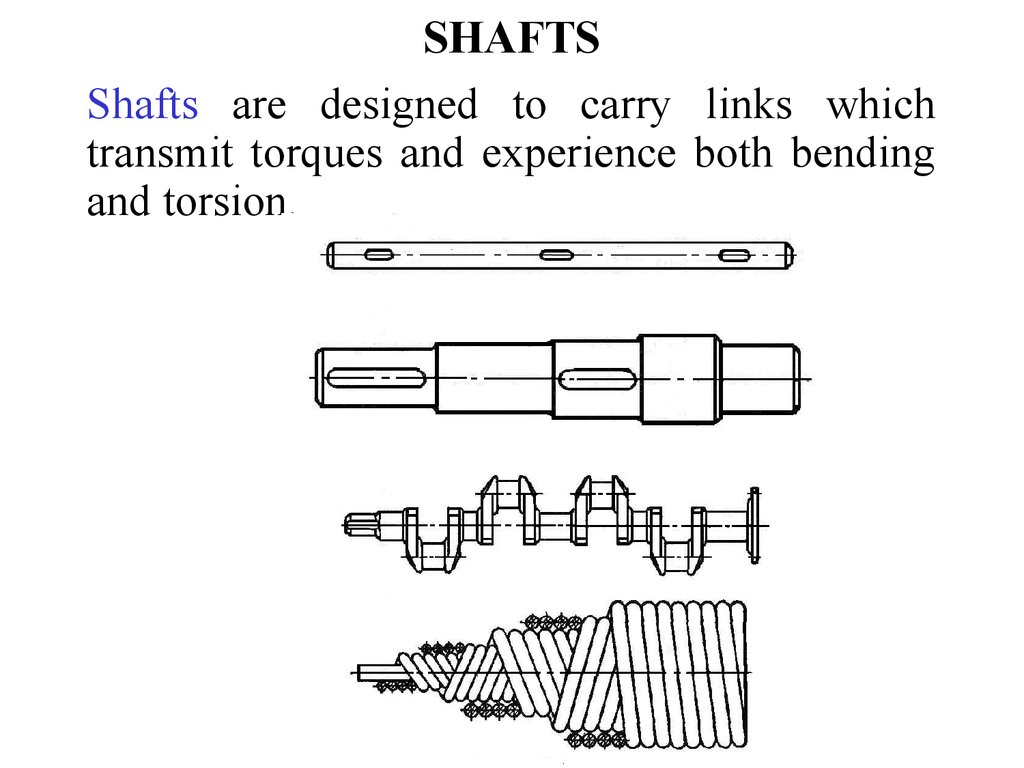
4. SHAFTS

Shafts are designed to carry links which
transmit torques and experience both bending
and torsion.

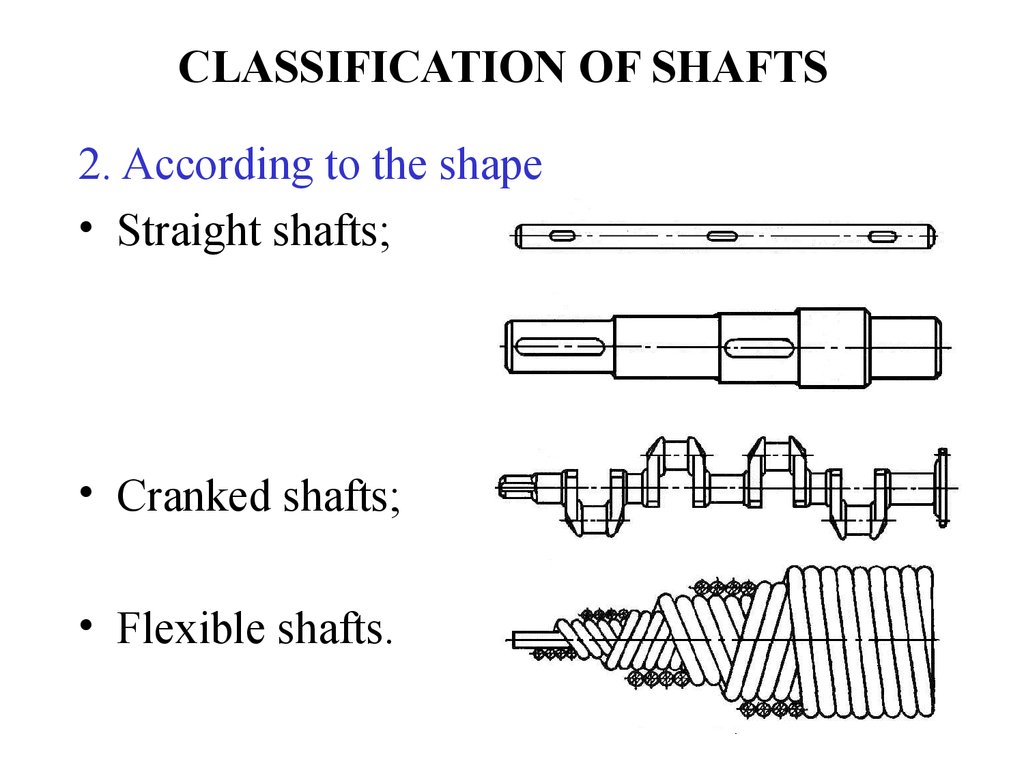
5. CLASSIFICATION OF SHAFTS

1. According to purpose
Shafts of various drives (gear drives, belt
drives, chain drives and so on);
Main shafts of mechanisms and machines
whose function is to carry not only drive
elements but other elements that do not
transmit torques such as rotors, flywheels, turbine disks, etc.

6. CLASSIFICATION OF SHAFTS

2. According to the shape
• Straight shafts;
• Cranked shafts;
• Flexible shafts.

7. CLASSIFICATION OF SHAFTS

3. According to the construction
• Shafts of constant cross section (without steps);
• Shafts of variable cross section (of stepped
configuration);
• Shafts made solid with gears or worms.

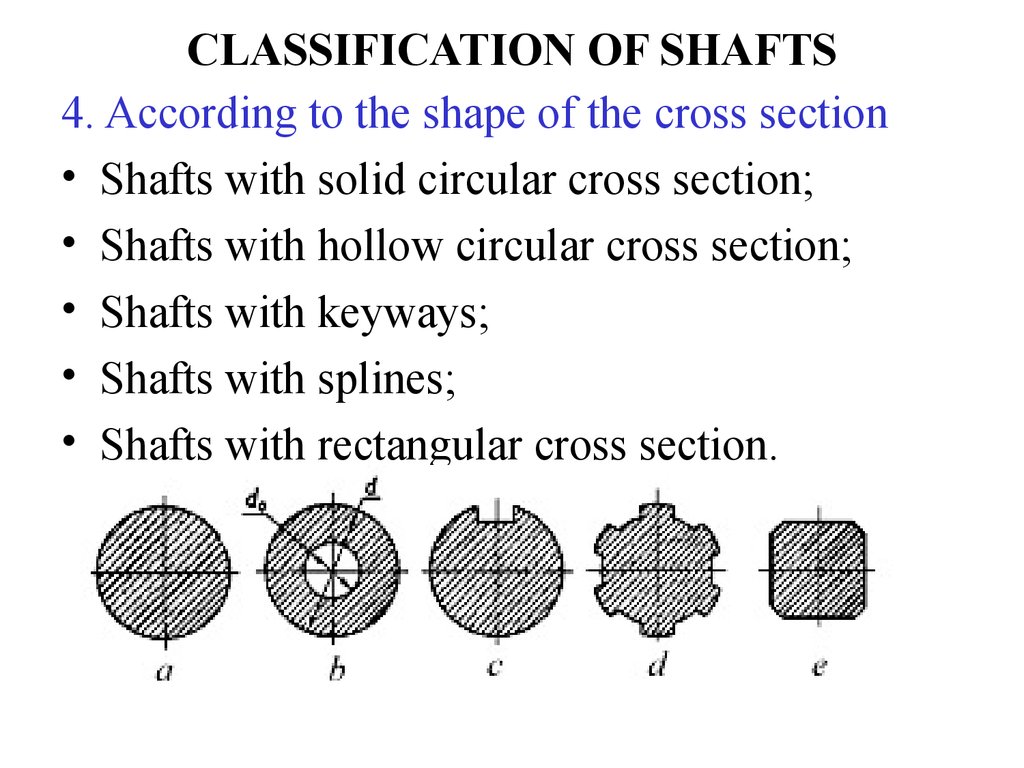
8. CLASSIFICATION OF SHAFTS

4. According to the shape of the cross section
• Shafts with solid circular cross section;
• Shafts with hollow circular cross section;
• Shafts with keyways;
• Shafts with splines;
• Shafts with rectangular cross section.

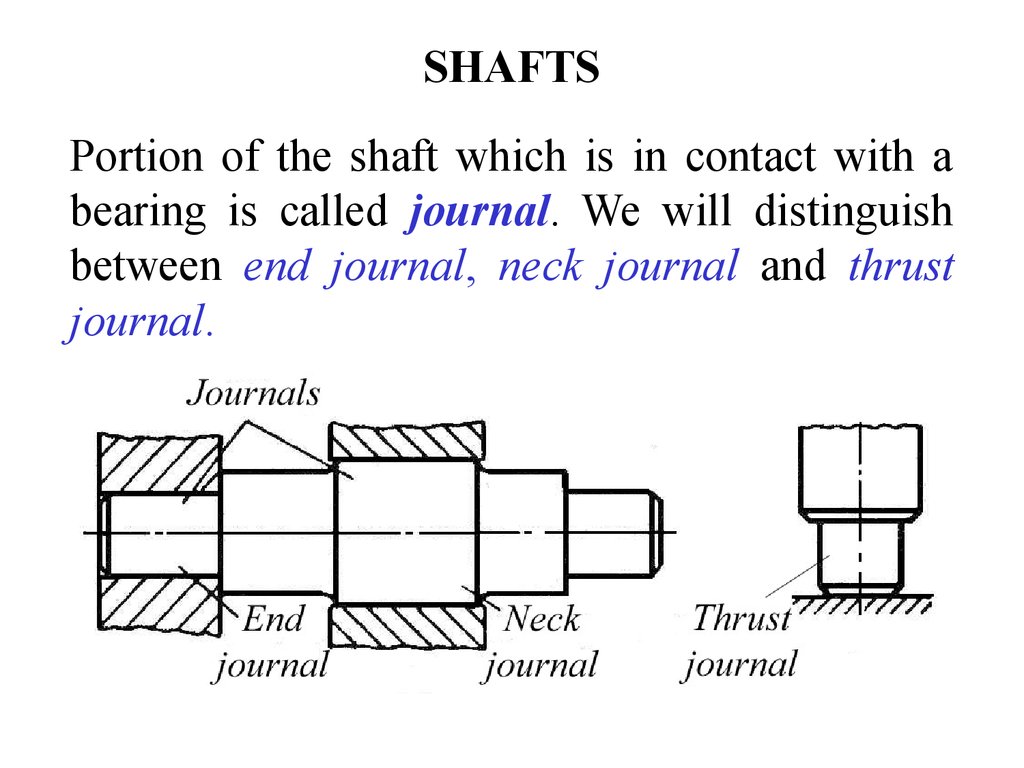
9. SHAFTS

Portion of the shaft which is in contact with a
bearing is called journal. We will distinguish
between end journal, neck journal and thrust
journal.

10. CALCULATION OF SHAFTS

Shafts may be calculated for:
• Strength;
• Rigidity;
• Oscillations.

11. CALCULATION OF SHAFTS FOR STRENGTH

Calculation of shafts for strength is
divided into 3 stages:
1. Determination of the minimum diameter
of the shaft;
2. Designing the shaft construction;
3. Strength analysis of the shaft.

12. DETERMINATION OF THE MINIMUM DIAMETER OF THE SHAFT

Minimum diameter of the shaft is determined
taking into account torsion stresses only. In
order to compensate neglect of bending
stresses the allowable torsion stress is
assumed as down rated ([ =20…40 MPa).
T
=
;
Wp
p×d
Wp =
.
16
T
d min = 3
.
0.2 × [ ]
3

13. DESIGNING THE SHAFT CONSTRUCTION

Input shaft
Half coupling
Bearing
d3
t1
d4
d3
t2
d2
t1
d1
d4
Pinion
Seal
d 1 = d min ;
d 2 = d 1 + 2 × t1 ;
d3 = d2 + 2 × t2 ;
d 4 = d 3 + 2 × t1 .
Bearing
d, mm
20…50
55…120
t1, mm
2; 2.5
5
t2 , mm
1; 1.5
2.5

14. SEALS

Seals are divided into:
• Commercial seals
(Lip-type seals);
• Labyrinth seals;
• Groove seals;
• Combined seals.
Rubbing element
Steel ring of L-shaped
cross-section
Coil spring

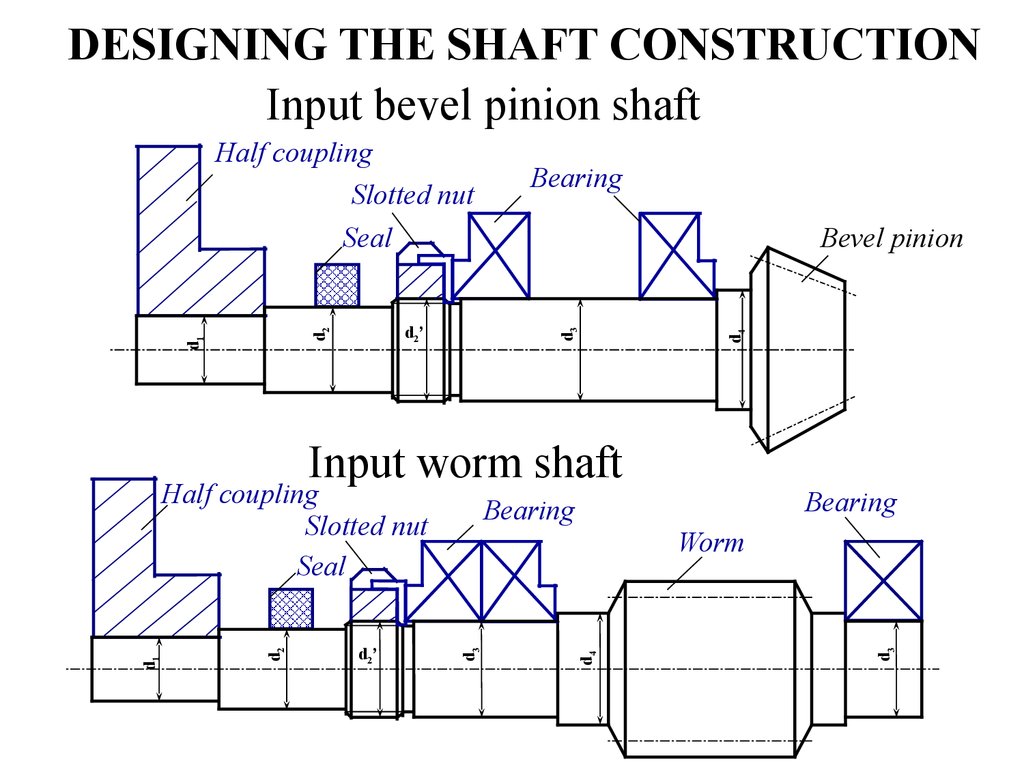
15. DESIGNING THE SHAFT CONSTRUCTION

Input bevel pinion shaft
Bevel pinion
d3
Input worm shaft
Worm
d4
d 2’
Bearing
Bearing
d3
d2
d1
Half coupling
Slotted nut
Seal
d3
d1
d2
d2 ’
Bearing
d4
Half coupling
Slotted nut
Seal

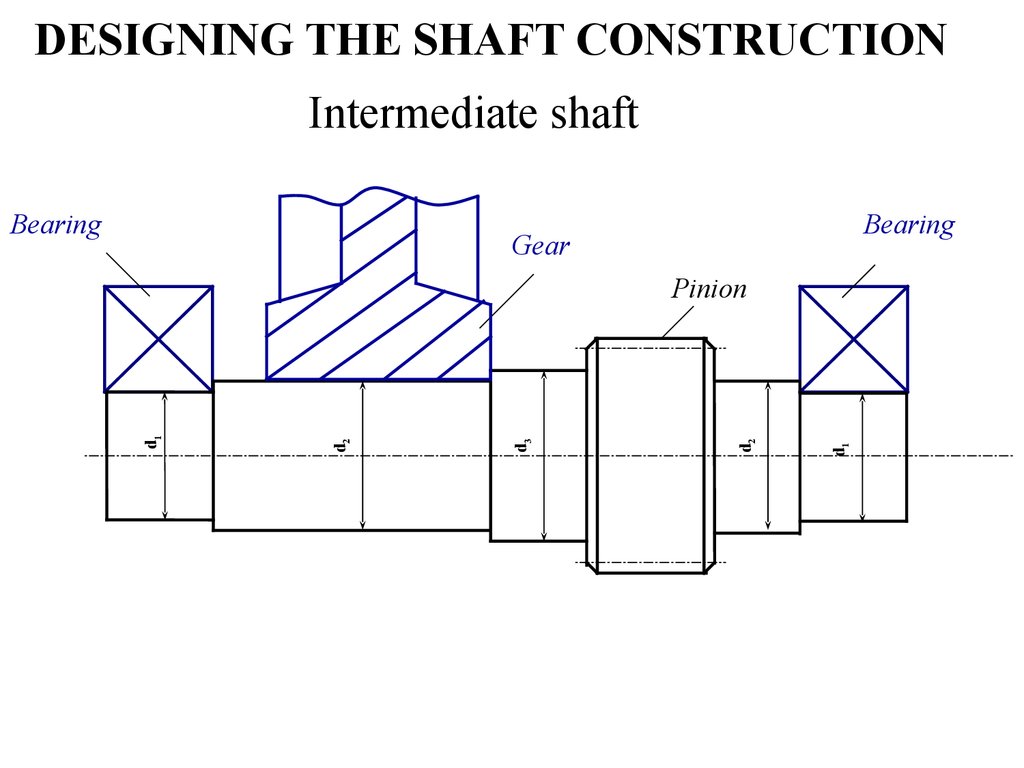
16. DESIGNING THE SHAFT CONSTRUCTION

Intermediate shaft
Bearing
Bearing
Gear
d1
d2
d3
d2
d1
Pinion

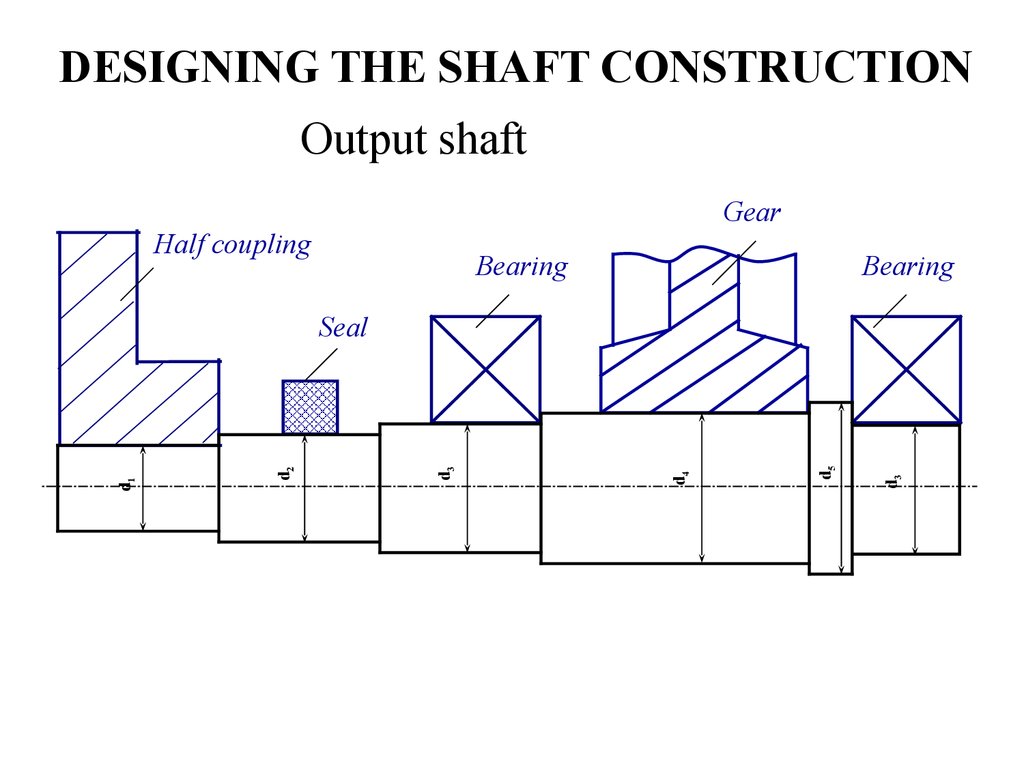
17. DESIGNING THE SHAFT CONSTRUCTION

Output shaft
Gear
Half coupling
Bearing
Bearing
d3
d5
d4
d3
d2
d1
Seal

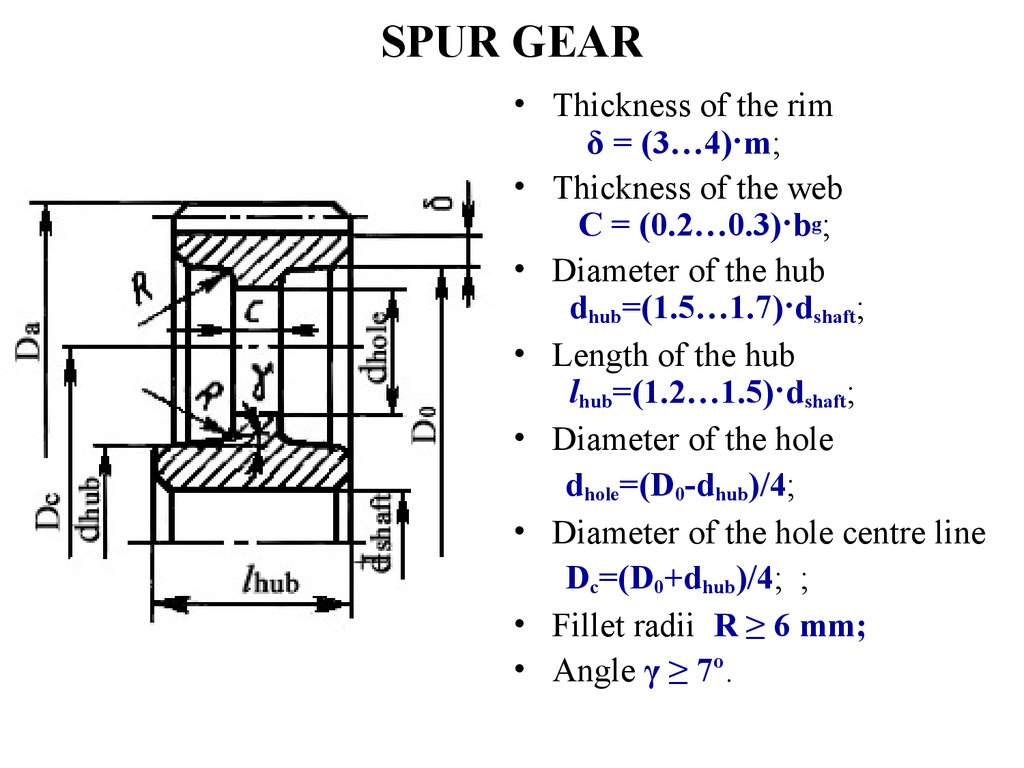
18. SPUR GEAR

• Thickness of the rim
δ = (3…4)·m;
• Thickness of the web
C = (0.2…0.3)·bg;
• Diameter of the hub
dhub=(1.5…1.7)·dshaft;
• Length of the hub
lhub=(1.2…1.5)·dshaft;
• Diameter of the hole
dhole=(D0-dhub)/4;
• Diameter of the hole centre line
Dc=(D0+dhub)/4; ;
• Fillet radii R ≥ 6 mm;
• Angle γ ≥ 7º.

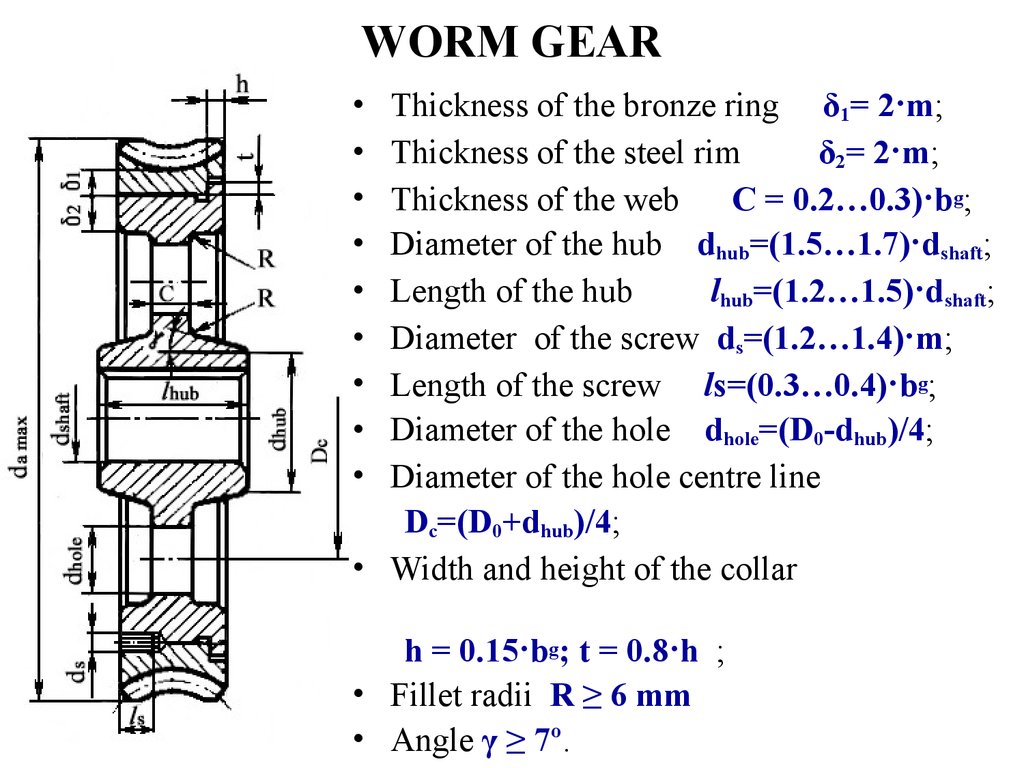
19. WORM GEAR

Thickness of the bronze ring δ1= 2·m;
Thickness of the steel rim
δ2= 2·m;
Thickness of the web
C = 0.2…0.3)·bg;
Diameter of the hub dhub=(1.5…1.7)·dshaft;
Length of the hub
lhub=(1.2…1.5)·dshaft;
Diameter of the screw ds=(1.2…1.4)·m;
Length of the screw ls=(0.3…0.4)·bg;
Diameter of the hole dhole=(D0-dhub)/4;
Diameter of the hole centre line
Dc=(D0+dhub)/4;
• Width and height of the collar
h = 0.15·bg; t = 0.8·h ;
• Fillet radii R ≥ 6 mm
• Angle γ ≥ 7º.

20. SKETCH LAYOUT

Double stage spur gear speed reducer
20
3…4
lhalf coupl
a
ssg
w
I
20
I
10
10
10
0.5B
10
1.25m
m
m
1.25m
0.5B
awhsg
3…4
10
20
B
10
10
20
lhub

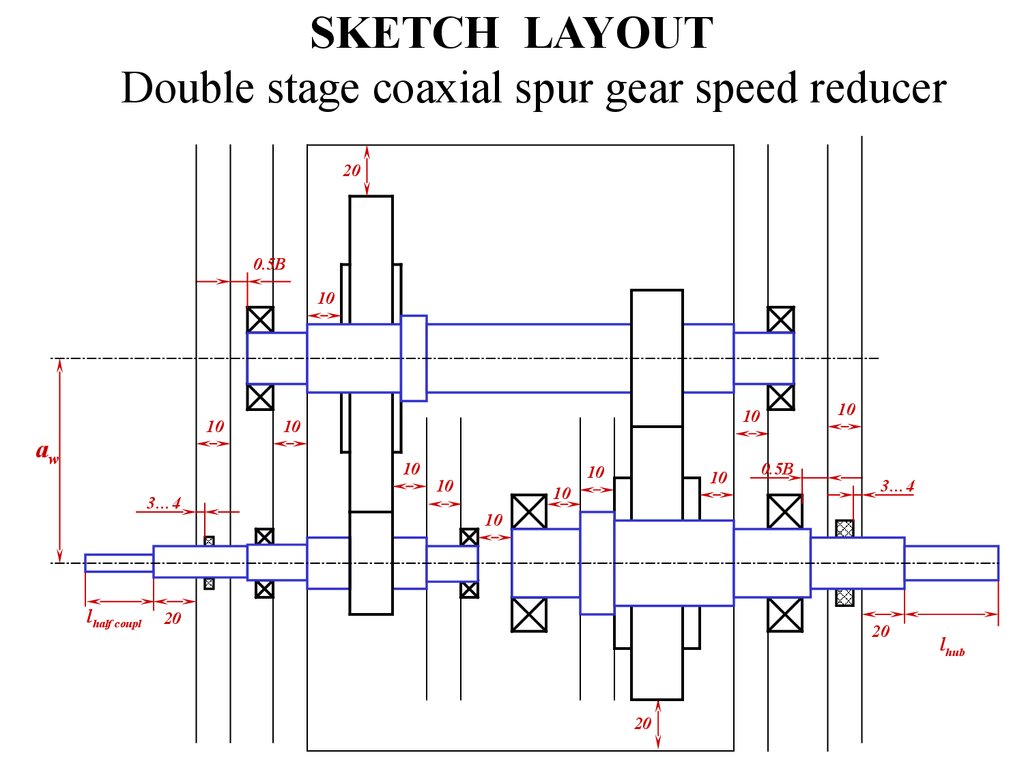
21. SKETCH LAYOUT

Double stage coaxial spur gear speed reducer
20
0.5B
10
10
aw
10
3…4
lhalf coupl
10
10
10
10
10
10
10
0.5B
3…4
10
20
20
20
lhub

22. SKETCH LAYOUT

Bevel gears
deg
me
bg
1.2me
dep
C
lhub
10
dhub

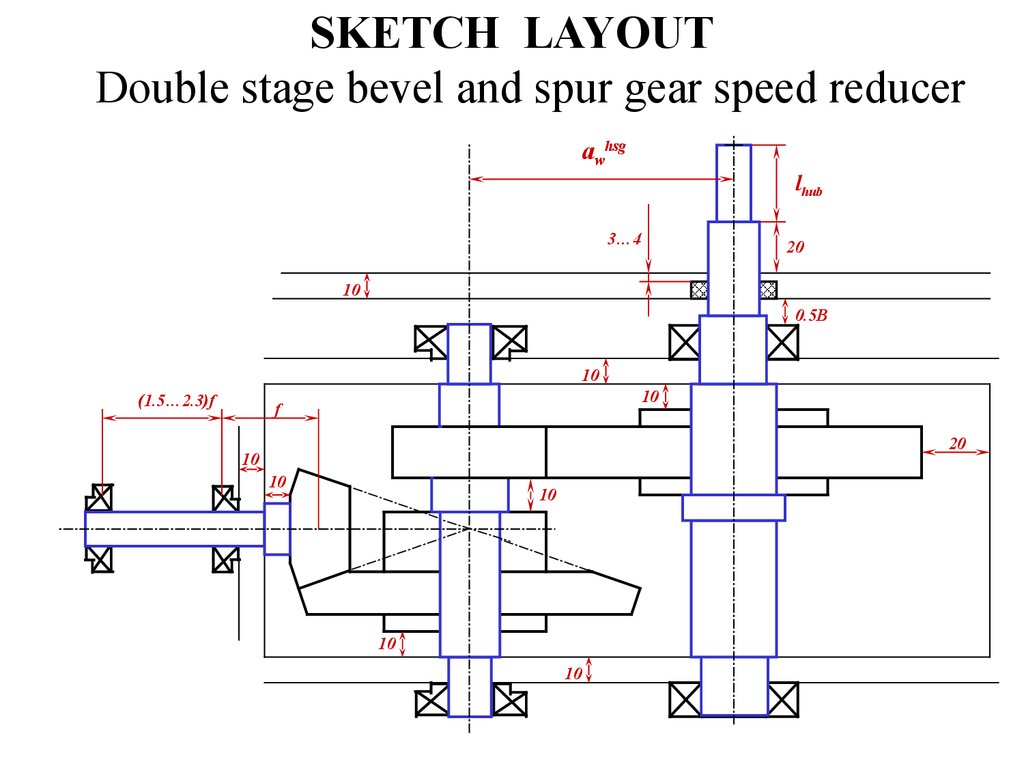
23. SKETCH LAYOUT

Double stage bevel and spur gear speed reducer
awhsg
lhub
3…4
20
10
0.5B
10
(1.5…2.3)f
10
f
20
10
10
10
10
10

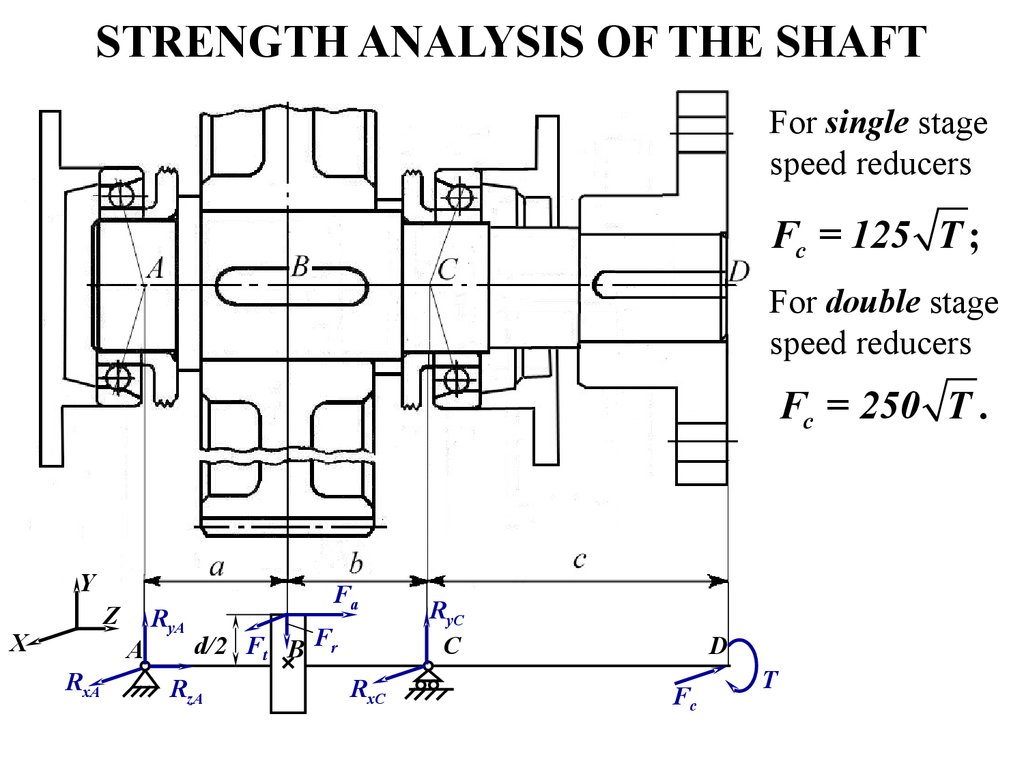
24. STRENGTH ANALYSIS OF THE SHAFT

For single stage
speed reducers
Fc = 125 T ;
For double stage
speed reducers
Fc = 250 T .
Y
Z
X
A
RxA
RyA
Fa
d/2 Ft B Fr
RzA
RxC
RyC
C
D
Fc
T

25. STRENGTH ANALYSIS OF THE SHAFT

1. Draw the analytical model in the vertical plane and transfer all forces
to the shaft;
2. Determine vertical support reactions RyA and RyC. For this purpose we
set up equations of moments relative to points A and C. For checking
we will write equation of forces that are parallel to Y axis;
3. Plot the bending moment diagram in the vertical plane;
4. Draw the analytical model in the horizontal plane and transfer all
forces to the shaft;
5. Determine horizontal support reactions RxA and RxC. For that we set
up equations of moments relative to points A and C. For checking we
write equation of forces that are parallel to X axis;
6. Plot the bending moment diagram in the horizontal plane;
2
2
7. Plot the total bending moment diagram ( M å = M x + M y );
8. Plot the twisting moment diagram;
2
2
9. Plot the reduced moment diagram( M red = M t + 0.75 × T ).

26. STRENGTH ANALYSIS OF THE SHAFT

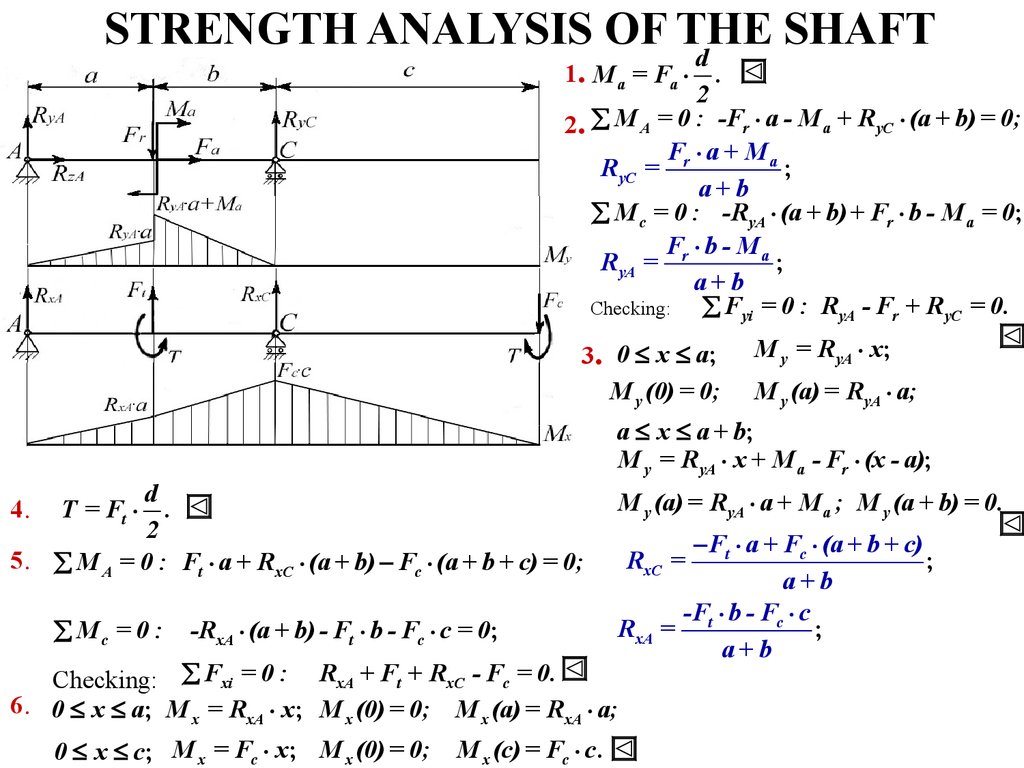
d
1. M a = Fa × .
2
2. å M A = 0 : -Fr × a - M a + R yС × (a + b) = 0;
F × a + Ma
R yC = r
;
a+b
å M c = 0 : -R yA × (a + b)+ Fr × b - M a = 0;
F × b - Ma
R yA = r
;
a+b
å Fyi = 0 : R yA - Fr + R yC = 0.
Checking:
3. 0 £ x £ a;
M y (0) = 0;
M y = R yA × x;
M y (a) = R yA × a;
a £ x £ a + b;
M y = R yA × x + M a - Fr × (x - a);
4.
5.
d
T = Ft × .
2
å M A = 0 : Ft × a + RxС × (a + b) - Fc × (a + b + c) = 0;
å Mc = 0 :
6.
-RxA × (a + b) - Ft × b - Fc × c = 0;
M y (a) = R yA × a + M a ; M y (a + b) = 0.
- Ft × a + Fc × (a + b + c)
;
a+b
-F × b - Fc × c
RxA = t
;
a+b
Checking: å Fxi = 0 : RxA + Ft + RxC - Fc = 0.
0 £ x £ a; M x = RxA × x; M x (0) = 0; M x (a) = RxA × a;
0 £ x £ c; M x = Fc × x; M x (0) = 0;
M x (c) = Fc × c .
RxC =

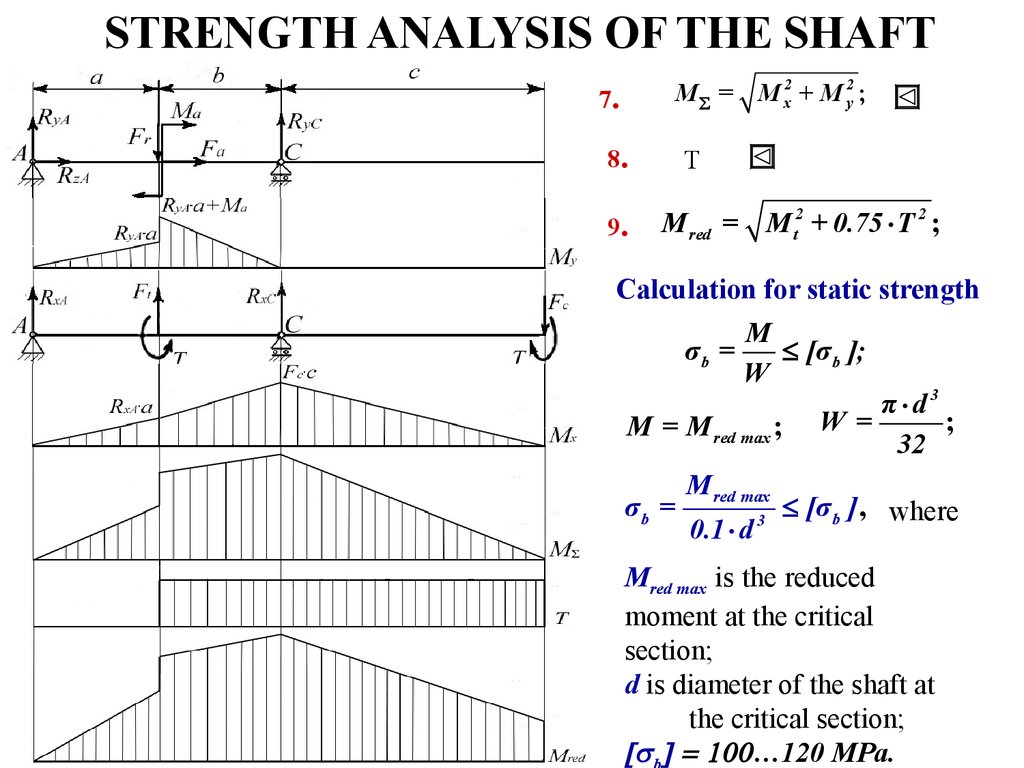
27. STRENGTH ANALYSIS OF THE SHAFT

M å = M x2 + M y2 ;
7.
8.
9.
T
M red = M t2 + 0.75 × T 2 ;
Calculation for static strength
σb =
M
£ [σ b ];
W
M = M red max ;
σb =
M red max
0.1 × d
3
π×d3
W=
;
32
£ [σ b ] , where
Mred max is the reduced
moment at the critical
section;
d is diameter of the shaft at
the critical section;
= …120 MPa.

28. STRENGTH ANALYSIS OF THE SHAFT

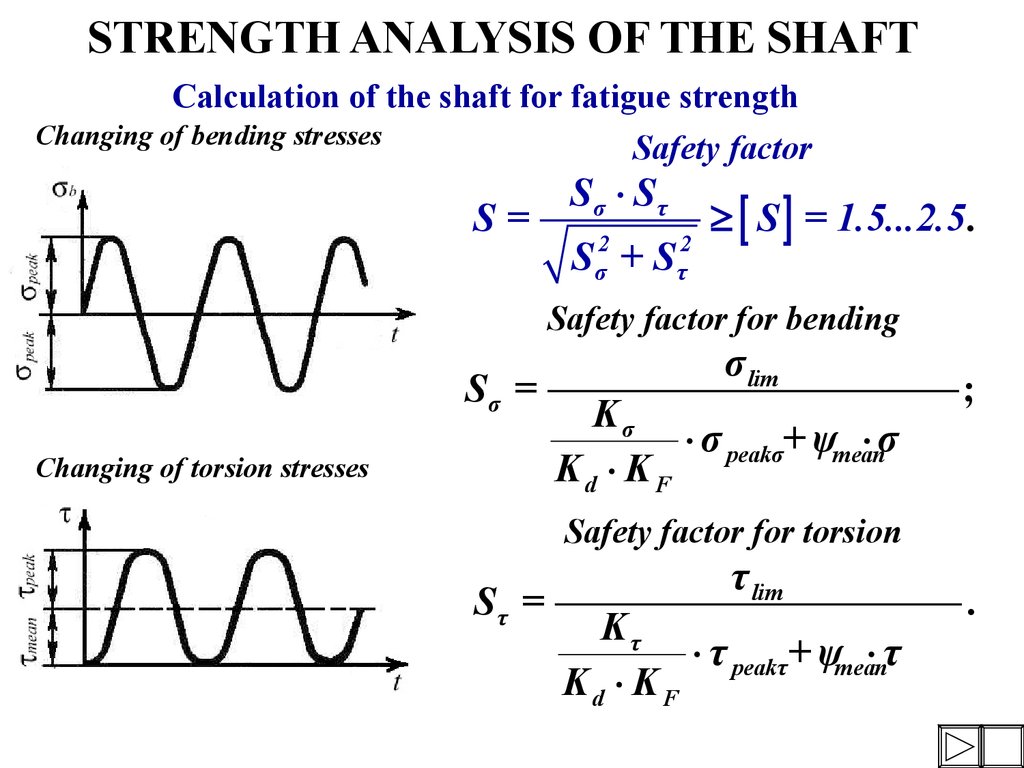
Calculation of the shaft for fatigue strength
Changing of bending stresses
Safety factor
S=
Sσ × S τ
Sσ2 + Sτ2
³ S = 1.5...2.5.
Safety factor for bending
Sσ =
Changing of torsion stresses
σ lim
Kσ
× σ peakσ+ ψmean
×σ
Kd × KF
;
Safety factor for torsion
Sτ =
τ lim
Kτ
× τ peakτ+ ψmean
×τ
Kd × KF
.

29. STRENGTH ANALYSIS OF THE SHAFT

Calculation of the shaft for fatigue strength
τ lim
σ lim
Sτ =
Sσ =
;
Kτ
Kσ
× τ peakτ+ ψmean
×τ
× σ peakσ+ ψmean
×σ
Kd × KF
K ×K
d
.
F
lim, lim – limit of endurance in bending and in torsion
σ lim = 0.43 × σ ult - for carbon steels;
σ lim = 0.35 × σ ult + 120 - for alloy steels;
τ lim = (0.2...0.3) × σ ult .
peak, peak – variable (peak) components of bending and torsion stresses
Må
Må
σ max - σ min
σ peak =
= σ max =
=
;
3
2
W
0.1 × d
τ peak
τ max + τ min τ max
T
T
=
=
= 0.5 ×
= 0.5 ×
.
3
2
2
Wp
0.2 × d

30. STRENGTH ANALYSIS OF THE SHAFT

Calculation of the shaft for fatigue strength
σ lim
τ lim
Sσ =
;
Sτ =
.
Kσ
Kτ
× σ peakσ+ ψmean
×σ
× τ peakτ+ ψmean
×τ
Kd × KF
Kd × KF
mean, mean– constant (mean) components of bending and torsion stresses
σ max + σ min
σ mean =
= 0;
2
τ max + τ min τ max
T
T
τ mean =
=
= 0.5 ×
= 0.5 ×
.
3
2
2
Wp
0.2 × d
– factors of constant components of bending and torsion stresses
= = - for carbon steels;
= = - for alloy steels.
K – effective stress concentration factors;
K d – scale factor;
K F - surface roughness factor.

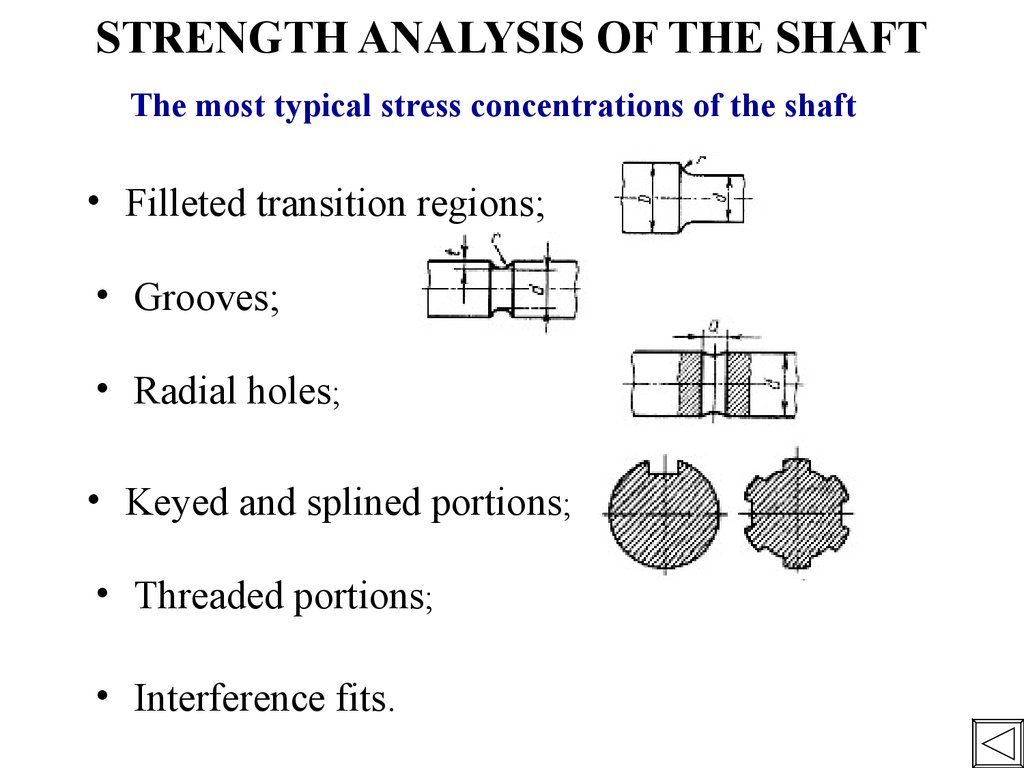
31. STRENGTH ANALYSIS OF THE SHAFT

The most typical stress concentrations of the shaft
• Filleted transition regions;
• Grooves;
• Radial holes;
• Keyed and splined portions;
• Threaded portions;
• Interference fits.

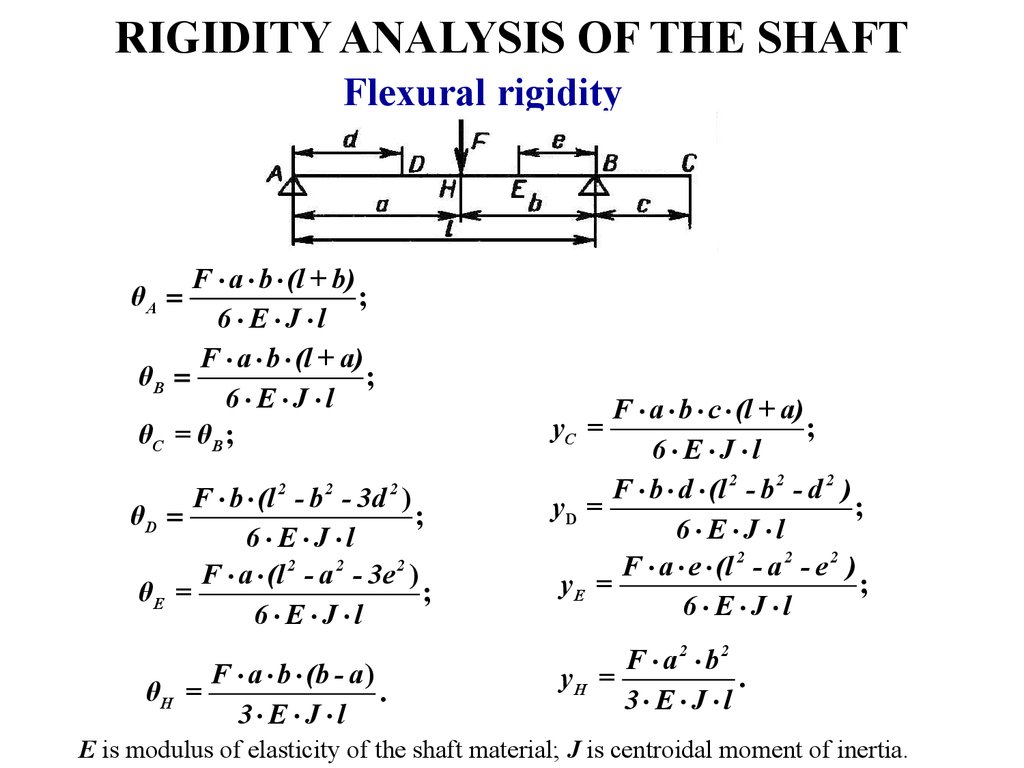
32. RIGIDITY ANALYSIS OF THE SHAFT

Flexural rigidity
Basic criteria of flexural rigidity are:
• Maximum deflection (sag) y of the shaft;
•Angle of rotation of support sections.
Flexural rigidity conditions
y £ y ;
θ £ θ ,
where
[y] is the maximum safe sag; is the maximum safe angle of
rotation.
[y]= 0.01m – for shafts of spur gears and worm gear drives;
[y]= 0.005m – for shafts of bevel gear, hypoid gear and hourglass
worm gear drives;
[y]= (0.0002…0.0003)l – for general purpose shafts used in machine
tools;
[ ]= 0.001 rad – for shafts mounted in sliding contact bearings;
[ ]= 0.005 rad – for shafts mounted in radial ball bearings.

33. RIGIDITY ANALYSIS OF THE SHAFT

Flexural rigidity
F × a × b × (l + b)
;
6× E ×J ×l
F × a × b × (l + a)
θB =
;
6× E ×J ×l
θC = θB ;
θA =
F × b × (l 2 - b 2 - 3d 2 )
θD =
;
6× E ×J ×l
F × a × (l 2 - a 2 - 3e 2 )
θE =
;
6×E ×J ×l
θH =
F × a × b × (b - a )
.
3× E ×J ×l
F × a × b × c × (l + a)
;
6× E ×J ×l
F × b × d × (l 2 - b 2 - d 2 )
yD =
;
6× E ×J ×l
F × a × e × (l 2 - a 2 - e 2 )
yE =
;
6× E ×J ×l
yC =
F × a 2 × b2
yH =
.
3× E ×J ×l
E is modulus of elasticity of the shaft material; J is centroidal moment of inertia.

34. RIGIDITY ANALYSIS OF THE SHAFT

Flexural rigidity
θA =
F1 × c × l
;
6×E×J
θB =
F1 × c × l
;
3× E ×J
θC =
F1 × c × (2 × l + 3 × c)
;
6×E×J
F1 × c × (3 × d 2 + l 2 )
θD =
;
6× E ×J ×l
F1 × c 2 × (l + c)
yC =
;
3× E ×J
F1 × c × d × (l 2 + d 2 )
yD =
.
6× E ×J ×l

35. RIGIDITY ANALYSIS OF THE SHAFT

Torsional rigidity
Basic criterion of torsional rigidity is the angle of twist.
Torsional rigidity condition
j £ j ,
where [j is the maximum safe angle of twist.
T ×l
j=
,
G × Jp
where T is torque; l is length of the shaft; G is shear modulus;
Jp= pd4/32 is polar moment of inertia.

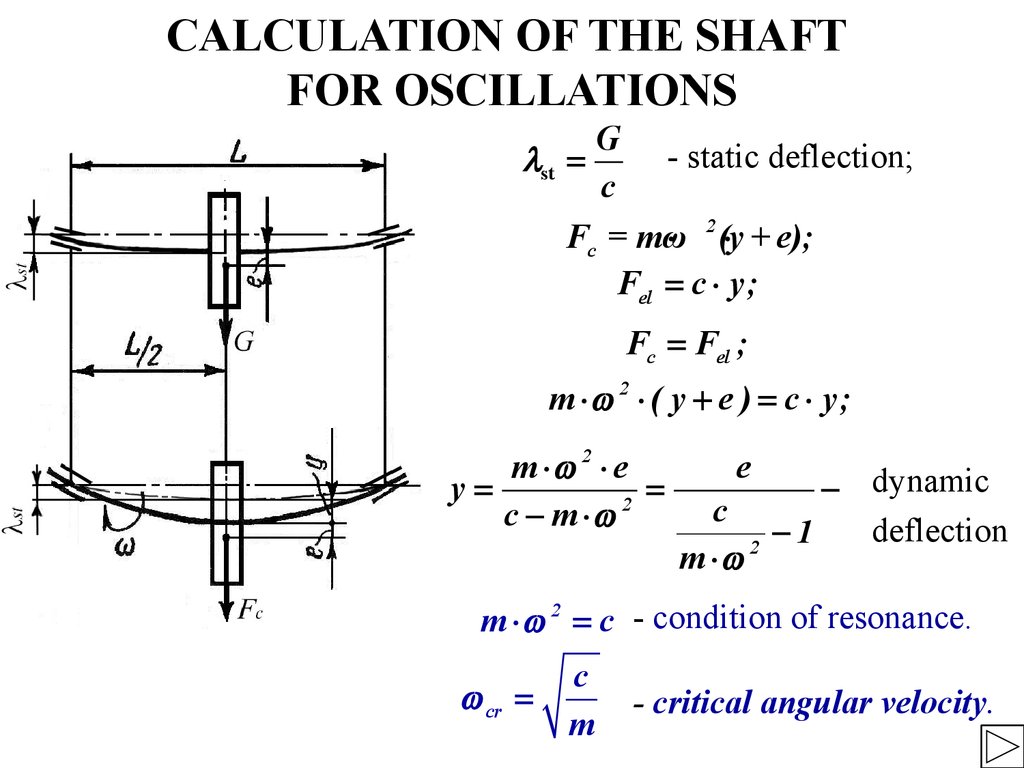
36. CALCULATION OF THE SHAFT FOR OSCILLATIONS

G
- static deflection;
lst =
c
Fc = mω
× 2 (y
× + e);
Fel = c × y;
Fc = Fel ;
m × w 2 × ( y + e ) = c × y;
m ×w 2 × e
y=
=
2
c - m ×w
e
c
m ×w 2
- dynamic
deflection
-1
m × w 2 = c - condition of resonance.
w cr =
c
m
- critical angular velocity.

37. CALCULATION OF THE SHAFT FOR OSCILLATIONS

p ×n
30
30
c 30
c × g 30
g
w=
Þ ncr =
× w cr =
×
=
×
=
×
;
30
p
p
m p
m×g p
lst
30
g
- critical rotational speed,
ncr =
×
p
lst
where
g = 9.81 m / sec 2 - free fall acceleration;
G
lst =
- static deflection;
c
48 × E × J
c=
- rigidity of the shaft;
3
L
E - modulus of elasticity of the shaft material;
L - distance between shaft supports;
p × d 4 - shaft moment of inertia.
J=
64

38. CALCULATION OF THE SHAFT FOR OSCILLATIONS

if n £ 0.7 × ncr - rigid shafts;
if n ³ 1.2 × ncr - flexible shafts.
y=
e
c
-1
2
m ×w
.
if w ® ¥ ,
y ® - e.
In this case we deal with shaft self-centering.