lection5-6_Konc_sistemnoi_dinamiki

1. ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ ЭКОНОМИЧЕСКИХ ПРОЦЕССОВ

Лекция 5-6
1

2. Концепции имитационного моделирования

Динамические системы
Системная динамика
Блочно-событийное моделирование
Агентное моделирование
2

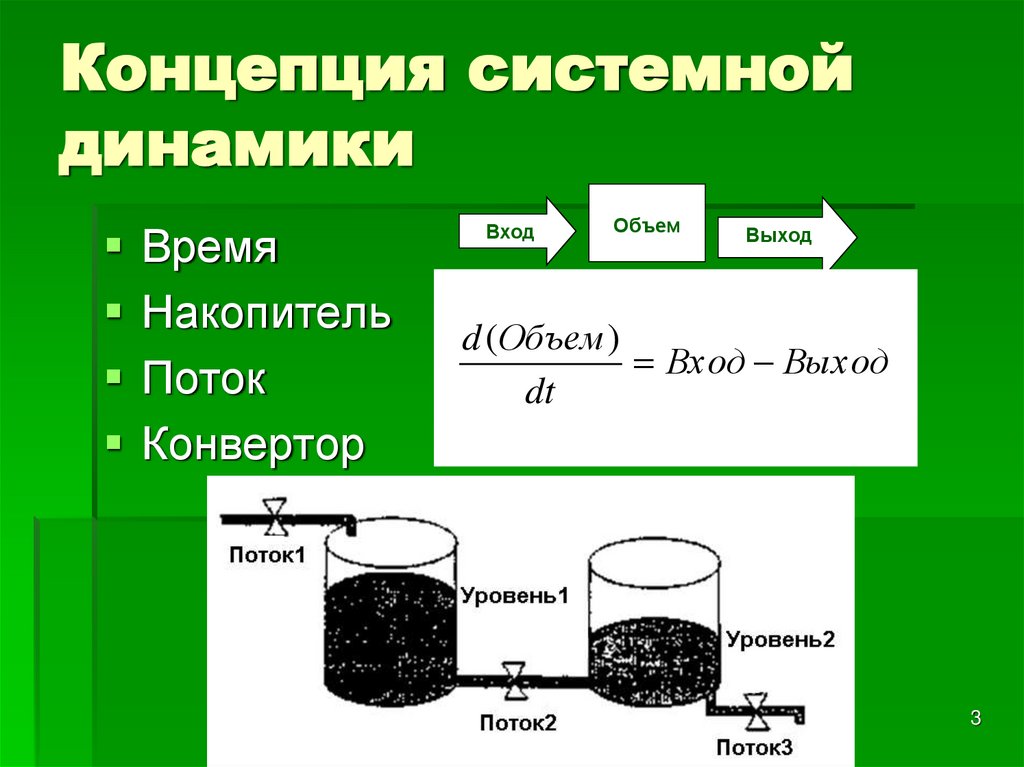
3. Концепция системной динамики

Время
Накопитель
Поток
Конвертор
Вход
Объем
Выход
d (Объем )
Вход Выход
dt
3

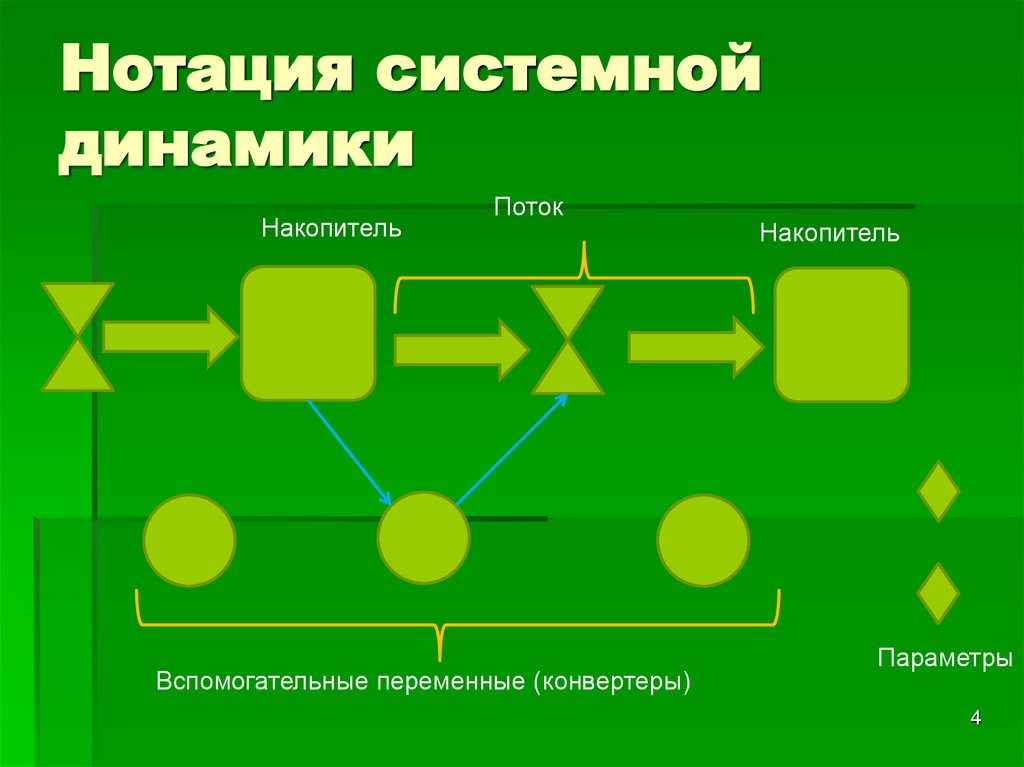
4. Нотация системной динамики

Накопитель
Поток
Вспомогательные переменные (конвертеры)
Накопитель
Параметры
4

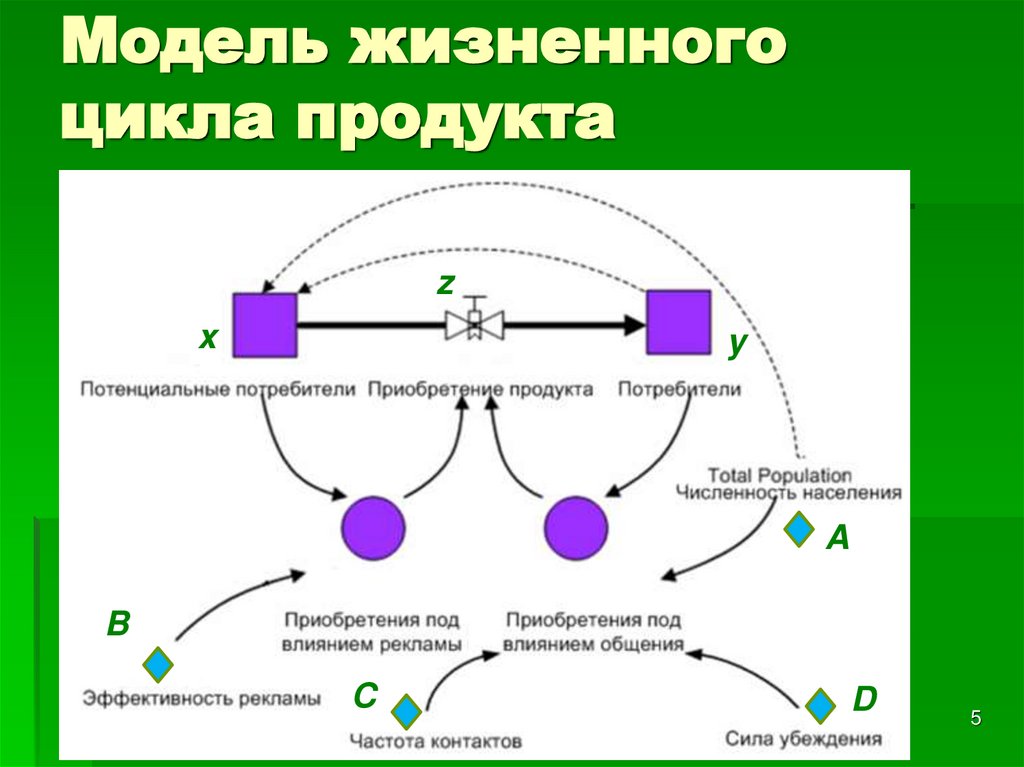
5. Модель жизненного цикла продукта

z
x
y
A
B
C
D
5

6. Формализация задачи

Параметры
А – Численность населения (100 000)
В – Эффективность рекламы (0.011)
С – Частота контактов (100)
F – Сила убеждения (0.015)
Переменные
x – потенциальные покупатели
y – владельцы товара
z – скорость приобретения продукта
(поток)
Вспомогательные переменные
Скорость приобретения продукта
под влиянием рекламы
Скорость приобретения продукта
под влиянием общения
r B x
x
s (C F y )
A
Общая скорость приобретения продукта
(поток)
z r s
ДУ изменения х и y
dx
z
dt
dy
z
dt
6

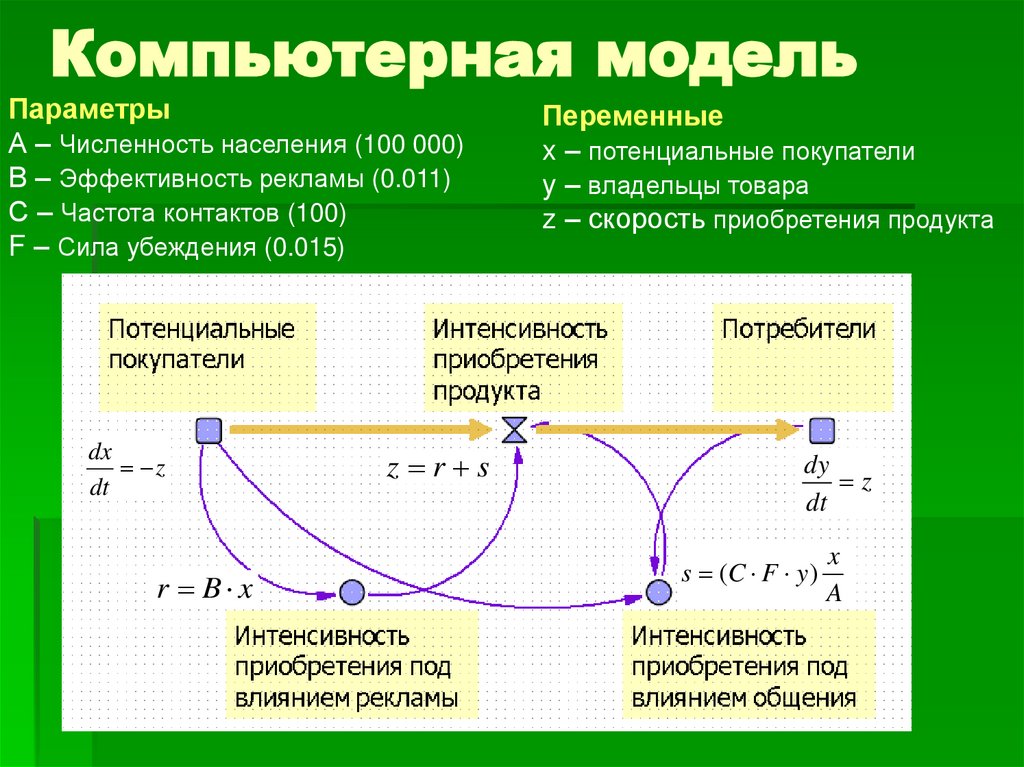
7. Компьютерная модель

Параметры
А – Численность населения (100 000)
В – Эффективность рекламы (0.011)
С – Частота контактов (100)
F – Сила убеждения (0.015)
dx
z
dt
r B x
z r s
Переменные
x – потенциальные покупатели
y – владельцы товара
z – скорость приобретения продукта
dy
z
dt
s (C F y )
x
A

8. Экспериментальный стенд

9. «Расходы по доходам» в нотации системной динамики

9

10. Epidemic Model - Various Experiments

Классическая модель распространения инфекционного заболевания. Изначально
все люди восприимчивы к заболеванию. Заболевание распространяется по мере
того, как зараженные люди контактируют и передают заболевание восприимчивым.
По прошествии определенного времени люди выздоравливают и приобретают
иммунитет. Модель содержит четыре эксперимента:
1. Простой эксперимент Simulation с заданными значениями параметров.
2. Калибровка Calibration: с помощью оптимизатора OptQuest мы находим
значения параметров, которые не могут быть измерены непосредственно в
реальном мире: подверженность заболеванию Infectivity и средняя
длительность заболевания AverageIllnessDuration. Оптимизатор находит
значения, минимизируя разницу между результатами моделирования и
измеренными историческими данными.
3. Эксперимент InstantCharts: типичный сценарий для системной динамики пользователь меняет значение параметра, и модель мгновенно выполняется с
новыми значениями, моментально отображая результаты. Этот эксперимент
создан на базе эксперимента сравнения прогонов.
4. Эксперимент InstantChartsAdvanced: аналогичен эксперименту InstantCharts, но
здесь моделирование выполняется и результаты перерисовываются прямо по
10
ходу изменения значения параметра с помощью бегунка.

11. Population and Carrying Capacity

Простая модель динамики изменения численности населения в области с
ограниченной пропускной способностью. Пропускная способность области,
согласно Дж. Штерману, - это то количество организмов, которое она может
поддерживать за счет имеющихся в ней ресурсов. В этой модели пропускная
способность будет постоянной. Есть только один накопитель - численность
населения Population. Мы полагаем, что система закрыта - в ней нет миграции, и
значение накопителя численности населения меняется только входящим потоком
рождений Births и исходящим потоком смертей Deaths. Построение модели
делится на четыре фазы. Вы можете запустить любую фазу модели, выбрав
соответствующий класс активного объекта в качестве корневого класса модели в
свойствах эксперимента.
11

12. Концепция блочно-событийного моделирования

13. Несколько исследуемых переменных

Модель 6. Выпуск продукции (две фирмы)
α1=const, α2=const – коэф. роста производства
Количество ресурса не ограничено
dx1
1 x1
dt
dx2
2 x2
dt
Решение: см. модель 2
13

14. Несколько исследуемых переменных

Модель 7. Борьба за ресурс (конкуренция)
α1=const, α2=const – коэф. роста производства
dx1
1 x1 1 f ( x1 , x2 ) x1
dt
dx2
2 x2 2 f ( x1 , x2 ) x2
dt
lim
x1 x2 0
f ( x1 , x2 ) 0
f ( x1 , x2 ) Функция учета совместного
lim f (0, xресурса
потребления
2 ) ; lim f ( x1 ,0)
x2
x1
14

15. Несколько исследуемых переменных

Модель 7. Борьба за ресурс (продолжение)
f ( x1 ,1.xНелинейная
x2
2 ) A1 xсистема
1 A2 ДУ
2. Не имеет аналитического решения
dx1
Необходимо
использовать
численные
3.
x
(
A
x
A
x
)
x
1 1
1
1 1
2 2
1
методы
dt
dx2
2 x2 2 ( A1 x1 A2 x2 ) x2
dt
A1=const, A2=const – коэф. потребления ресурса
каждой фирмой на ед. изделия
γ1=const, γ2=const – коэф. рациональности
15
использования ресурса

16. Модель 8. Соотношение продукта и ресурса

α1=const – коэф. естественной убыли продукта
скорость естественной убыли
dx1
1 x1 продукта в отсутствии ресурса
dt
α2=const – коэф. естественного роста ресурса
dx2
2 x2
dt
скорость естественного роста
ресурса
16

17. Соотношение продукта и ресурса (модель 8)

1 - коэф. использования ресурса
dx1
1 x1 1 x1 x2
dt
2 - коэф. убыли ресурса
dx2
2 x2 2 x1 x2
dt
17

18. Способы графического отображения процесса

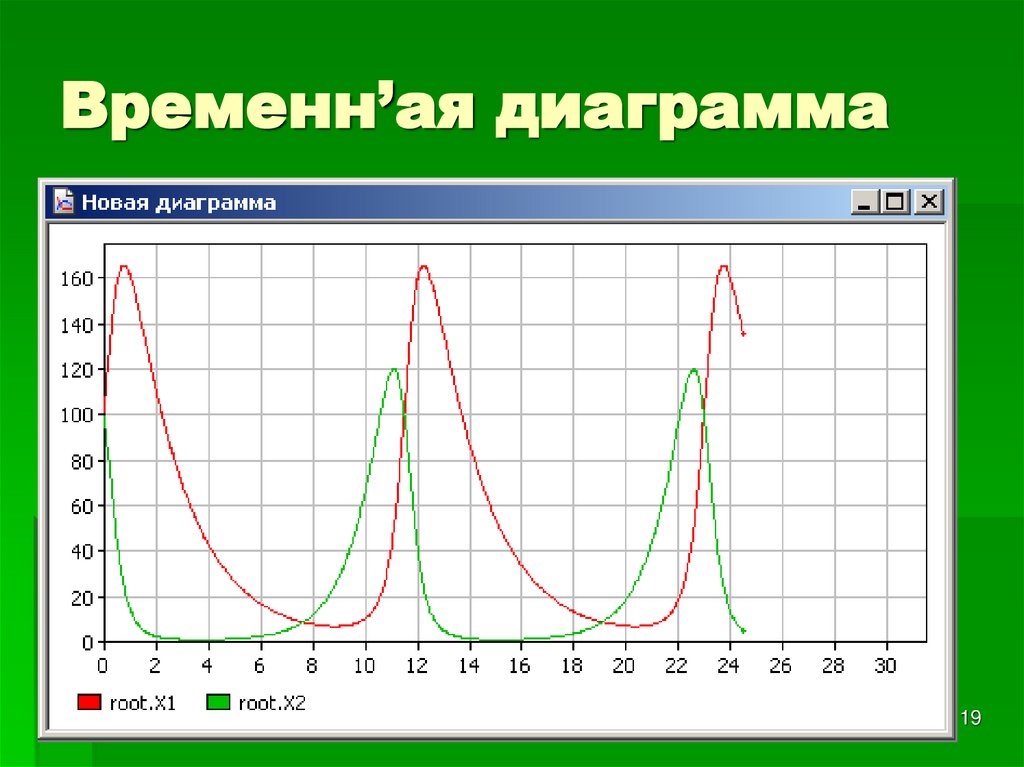
18

19. Временн’ая диаграмма

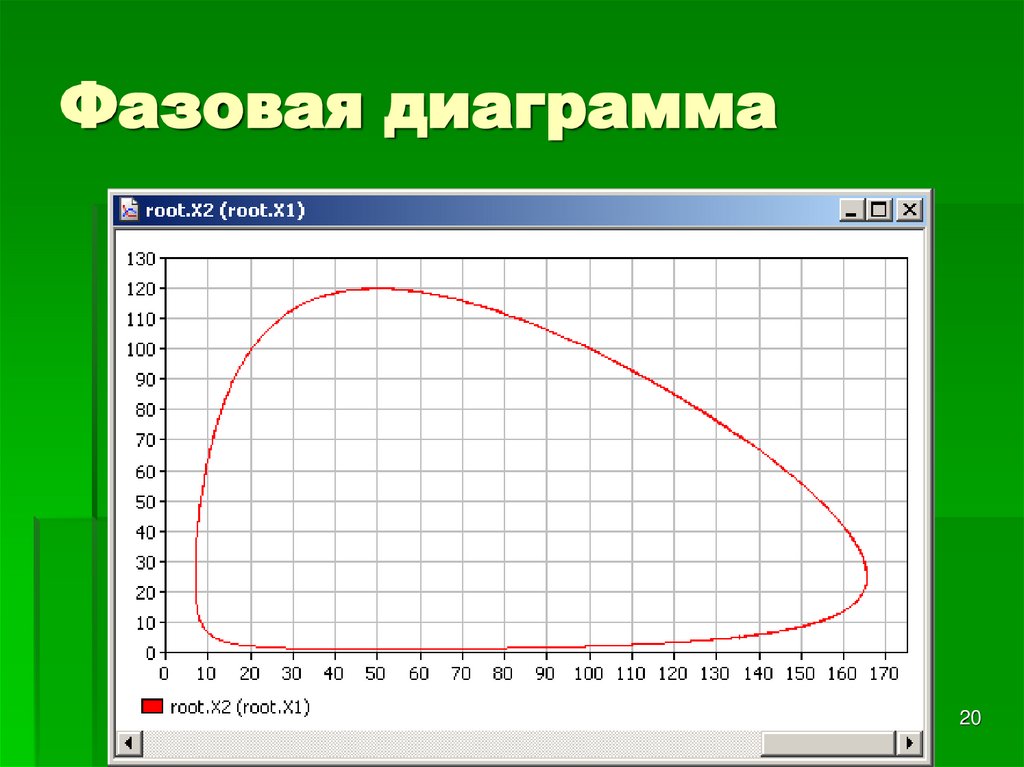
19

20. Фазовая диаграмма

20

21. Подходы к построению модели

1. Динамическая система
(один класс система ДУ с двумя
переменными)
ПродуктРесурс
21

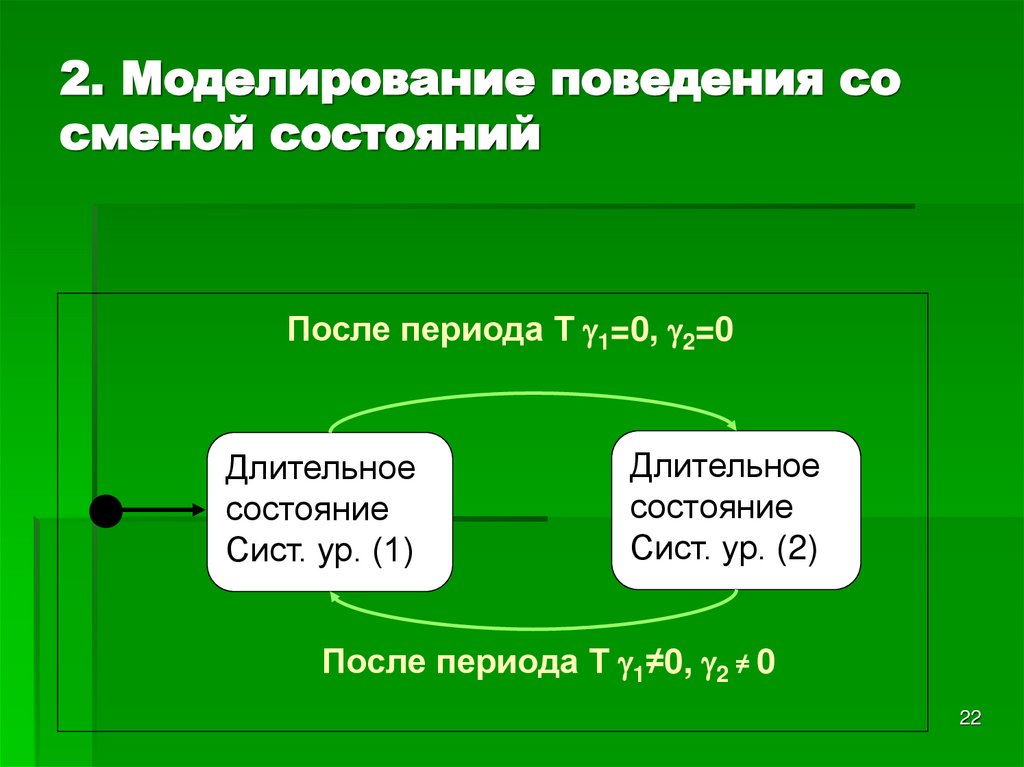
22. 2. Моделирование поведения со сменой состояний

После периода Т 1=0, 2=0
Длительное
состояние
Сист. ур. (1)
Длительное
состояние
Сист. ур. (2)
После периода Т 1≠0, 2 ≠ 0
22

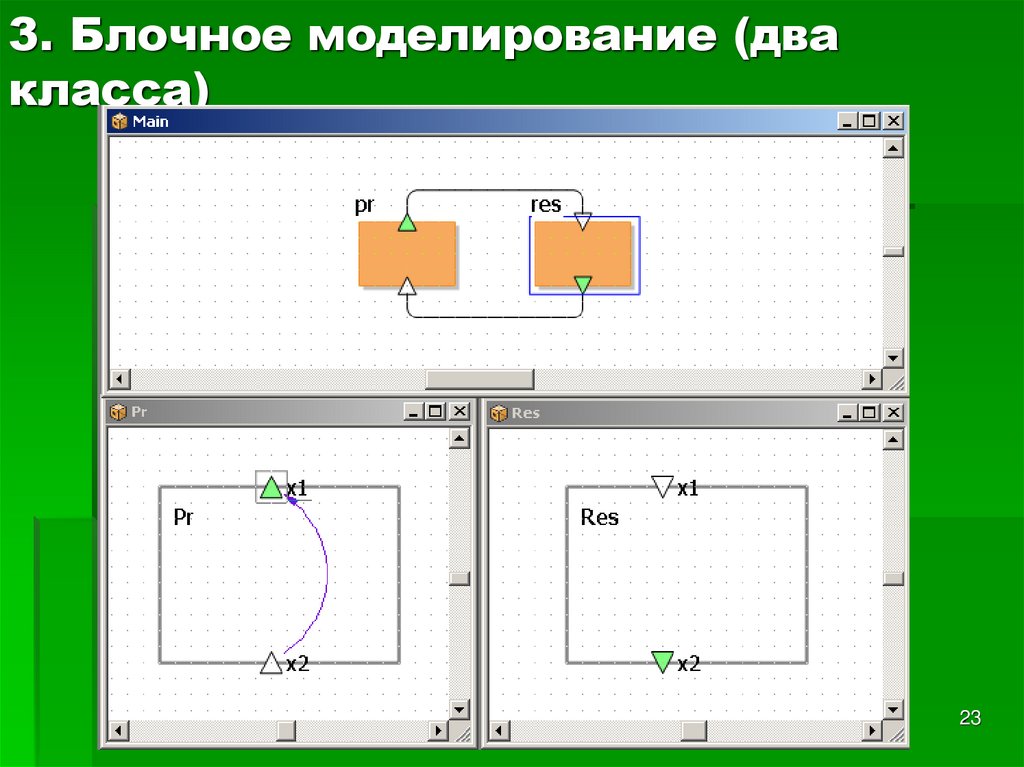
23. 3. Блочное моделирование (два класса)

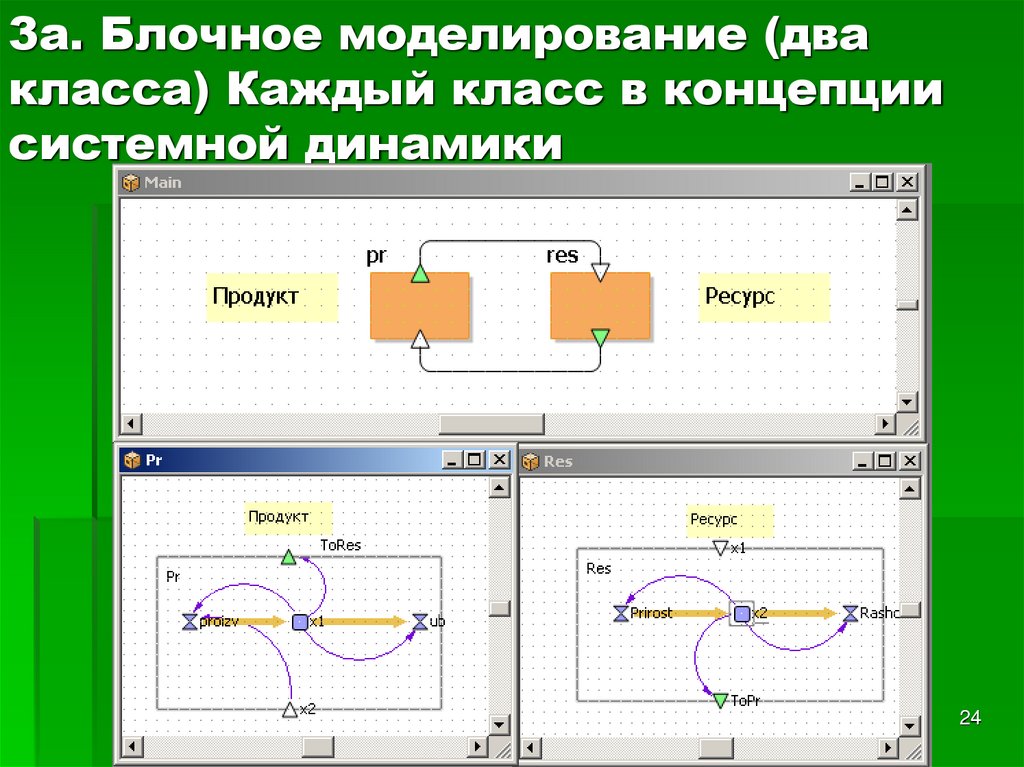
23

24. 3а. Блочное моделирование (два класса) Каждый класс в концепции системной динамики

24

25. 4. Разностные уравнения (дискретизация процесса)

Рассматривали модель 8 (Продукт-Ресурс)
Можно перейти к разностным уравнениям
dt t
dx
1 (i )
( i 1)
(
i) ~
(i )
(i )
~
x
x
x
x1
x1 11 x11 1 11x12 x2
dt
( i 1)
(i )
(i )
(i )
(i )
~
~
x2
dxx22 2 x2 2 x1 x2
2 x2 2 x1 x2
dt
25

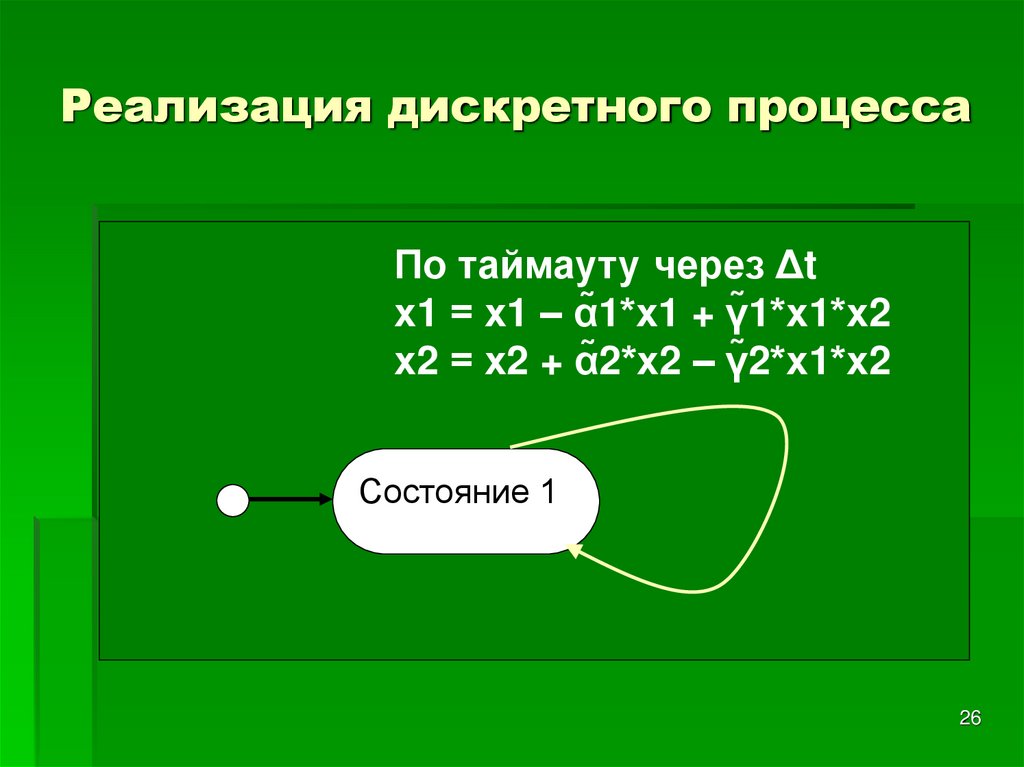
26. Реализация дискретного процесса

По таймауту через Δt
х1 = х1 – α̃1*х1 + γ̃1*х1*х2
х2 = х2 + α̃2*х2 – γ̃2*х1*х2
Состояние 1
26

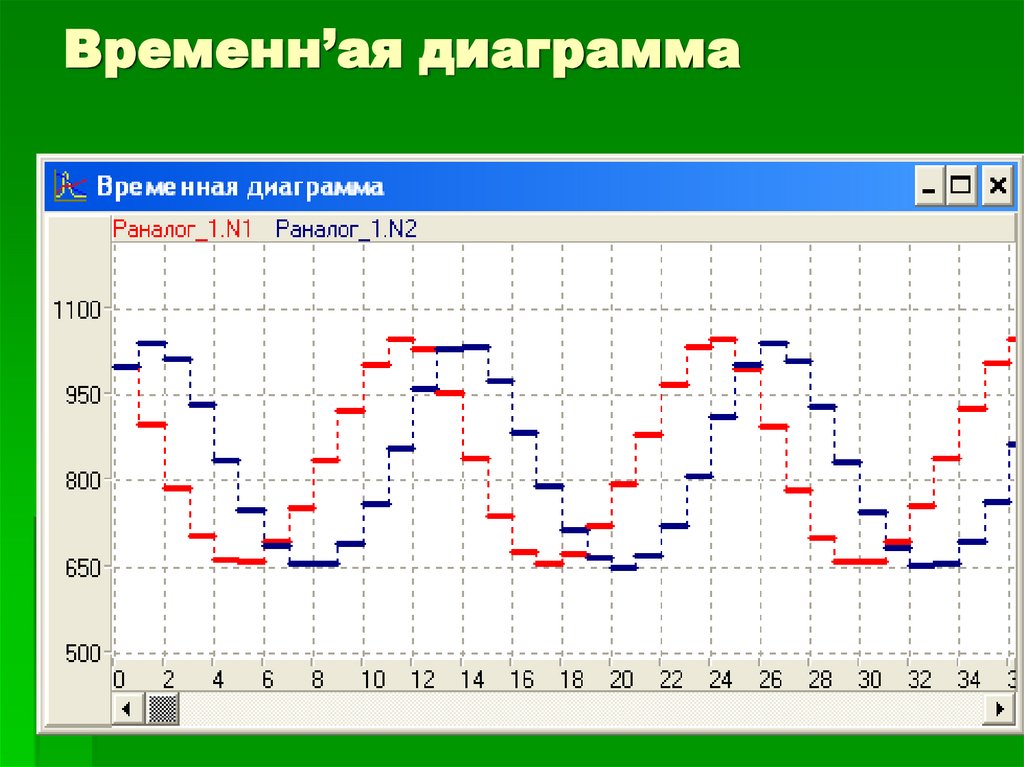
27. Временн’ая диаграмма

27

28. 5. Описание локальных законов поведения

Закон убыли продукта
Закон роста продукта
Закон роста ресурса
Закон убыли ресурса
x1
x1
( i 1)
( i 1)
x2
x2
( i 1)
( i 1)
x1
(i )
x1
(i )
(i )
~
x
1 1
(i )
(i )
~
x x
1 1
x2
(i )
x2
(i )
2
(i )
~
x
2 2
(i )
(i )
~
x x
2 1
2
28

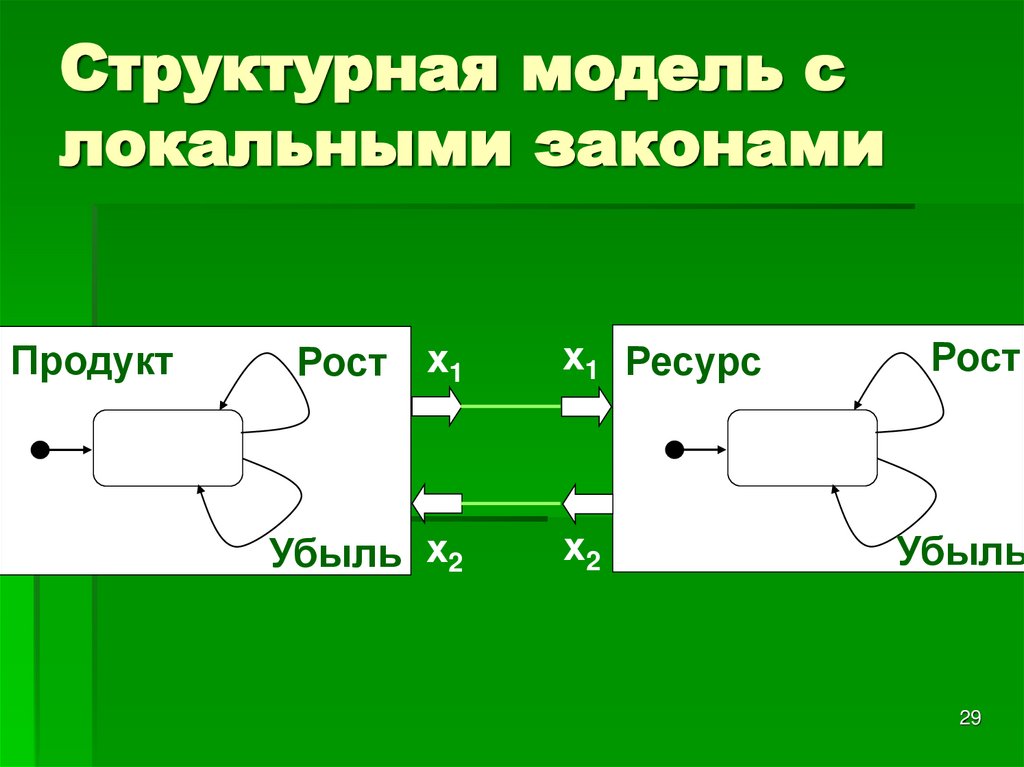
29. Структурная модель с локальными законами

Продукт
Рост х1
х1 Ресурс
Убыль х2
х2
Рост
Убыль
29

30. 6. Добавление случайности

В разностных уравнениях считать, что
~
~
~
~
1 , 1 , 2 , 2
случайные числа, распределенные в
1-м приближении по нормальному закону
30

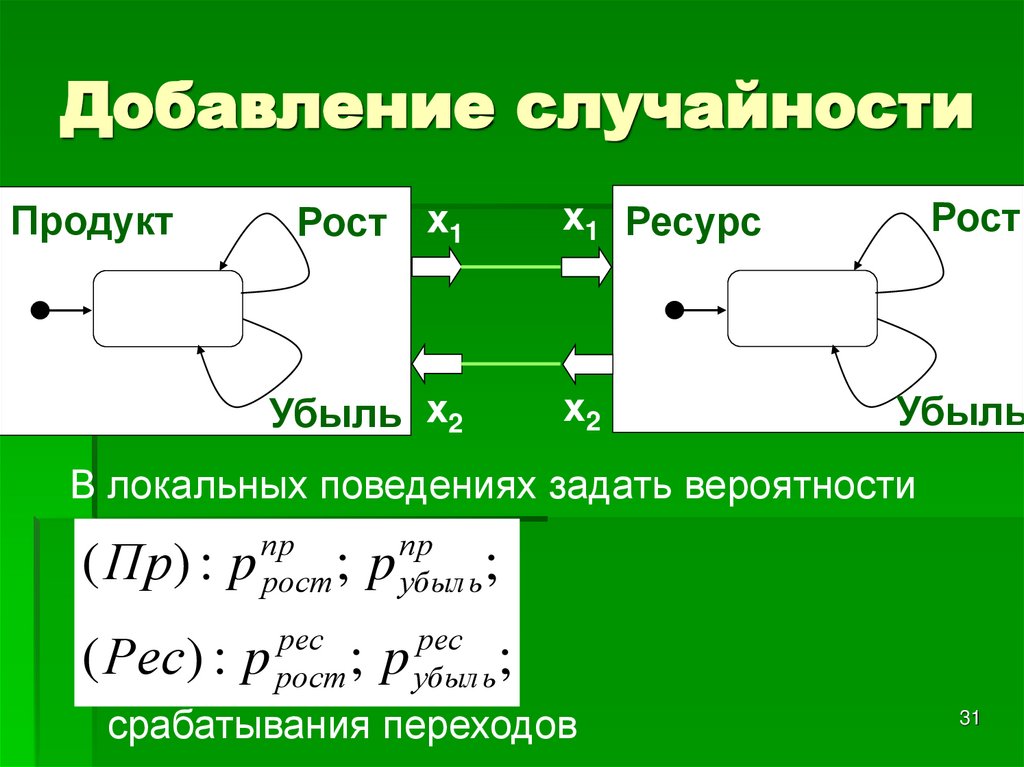
31. Добавление случайности

Рост х1
х1 Ресурс
Убыль х2
х2
Продукт
Рост
Убыль
В локальных поведениях задать вероятности
( Пр) : p
пр
рост
( Рес) : p
;p
рес
рост
пр
убыль
;p
;
рес
убыль
;
срабатывания переходов
31