3_3 Ан_Геом_Поверхности24

1.

§ 5. Поверхности второго порядка.
Метод сечений
Опр. 1. Поверхностью 2-го порядка называется поверхность,
определяемая в декартовой прямоугольной системе координат в
пространстве алгебраическим уравнением 2-й степени с тремя
переменными, т. е. уравнением вида
a11x2+ a22y2 + a33z2 + 2a12xy + 2a13xz + 2a23yz + 2a1x + 2a2y +2a3z + a0 = 0,
в котором хотя бы один из коэффициентов a11, a22, a33, a12, a13, a23 не
равен 0.
Поверхности второго порядка делятся на 1) вырожденные и 2)
невырожденные
Вырожденные поверхности второго порядка это плоскости и точки,
которые задаются уравнением второй степени. Если уравнению второго
порядка не удовлетворяет ни одна точка пространства, то тоже говорят,
что уравнение определяет вырожденную поверхность (мнимую
поверхность второго порядка).
Невырожденными поверхности второго порядка подразделяются
на пять типов

2.

В зависимости от значений коэффициентов это уравнение
определяет поверхности следующих типов:
1) эллиптический (эллипсоид, частный случай – сфера);
2) гиперболический (однополостный
гиперболоиды, коническая поверхность);
и
двуполостный
3) параболический (эллиптический и гиперболический
параболоиды);
4)
цилиндрические
поверхности
(эллиптический,
гиперболический,
параболический
цилиндры,
пара
пересекающихся или пара параллельных плоскостей);
5) конический (конус)

3.

Метод сечений
При изучении формы поверхностей используется метод сечений, который
состоит в том, что поверхность рассекают плоскостями и по виду линий
пересечения делают вывод о форме самой поверхности.
Сфера
Опр. 2. Сфера – множество точек пространства, равноудаленных от
данной точки M0(x0; y0,z0), которая называется центром сферы. Расстояние R
от центра до точек сферы называется ее радиусом.
Если M(x; y, z) – произвольная точка на сфере,
то, по определению, расстояние от точки M до
точки M0 должно быть равно R, поэтому
( x x0 ) 2 ( y y0 ) 2 ( z z0 )2 R;
( x x0 )2 ( y y0 )2 ( z z0 )2 R 2 .
Если x0 = 0, y0 = 0, z0 = 0, то уравнение сферы с центром в начале
координат имеет вид
x2 y 2 z 2 R2 .

4.

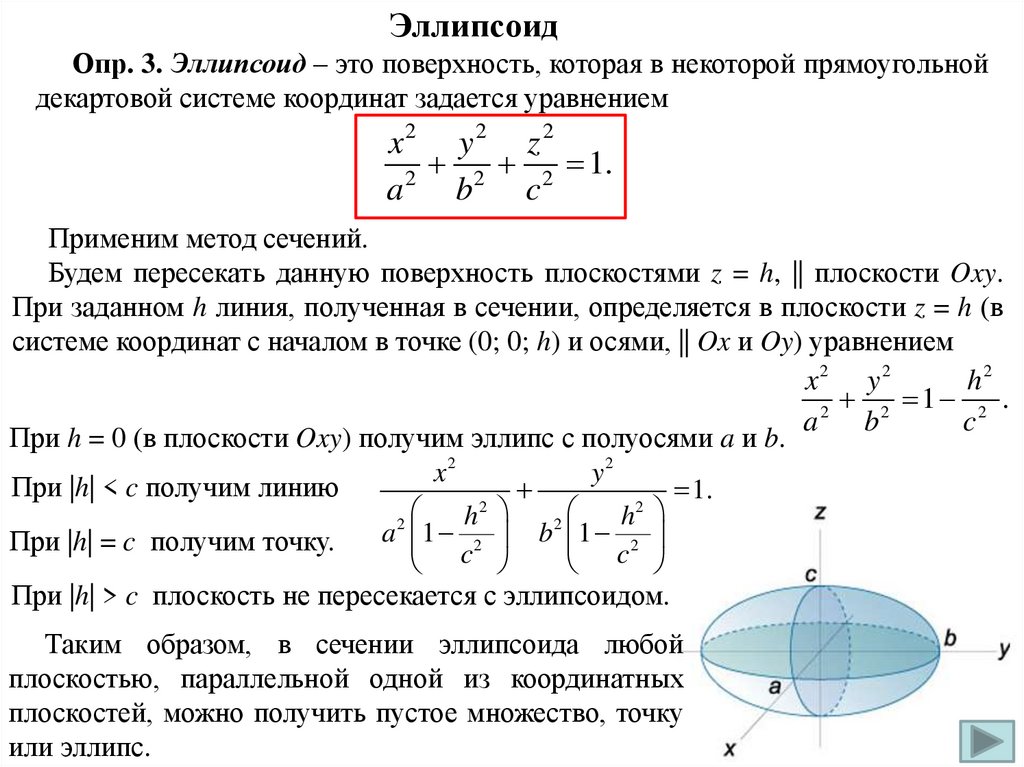
Эллипсоид
Опр. 3. Эллипсоид – это поверхность, которая в некоторой прямоугольной
декартовой системе координат задается уравнением
x2 y 2 z 2
2 2 1.
2
a
b
c
Применим метод сечений.
Будем пересекать данную поверхность плоскостями z = h, || плоскости Oxy.
При заданном h линия, полученная в сечении, определяется в плоскости z = h (в
системе координат с началом в точке (0; 0; h) и осями, || Ox и Oy) уравнением
x2 y 2
h2
2 1 2 .
2
a
b
c
При h = 0 (в плоскости Oxy) получим эллипс с полуосями a и b.
x2
y2
При |h| < c получим линию
1.
2
2
h
h
2
2
a 1 2 b 1 2
При |h| = c получим точку.
c
c
При |h| > c плоскость не пересекается с эллипсоидом.
Таким образом, в сечении эллипсоида любой
плоскостью, параллельной одной из координатных
плоскостей, можно получить пустое множество, точку
или эллипс.

5.

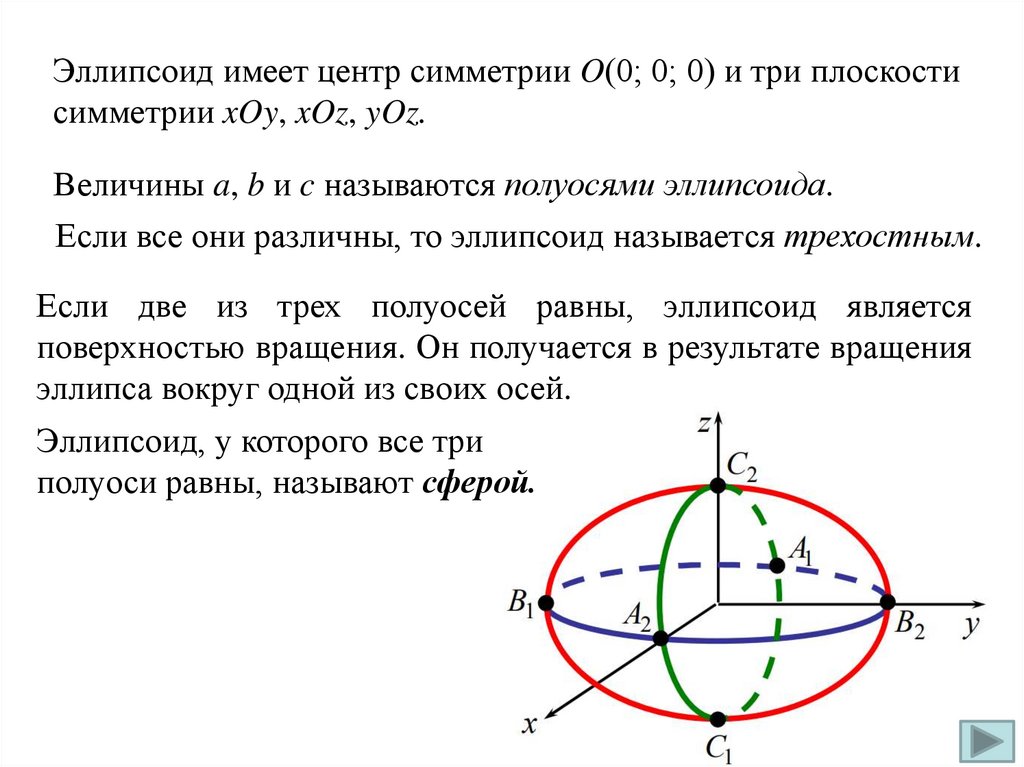
Эллипсоид имеет центр симметрии O(0; 0; 0) и три плоскости
симметрии xOy, xOz, yOz.
Величины a, b и c называются полуосями эллипсоида.
Если все они различны, то эллипсоид называется трехостным.
Если две из трех полуосей равны, эллипсоид является
поверхностью вращения. Он получается в результате вращения
эллипса вокруг одной из своих осей.
Эллипсоид, у которого все три
полуоси равны, называют сферой.

6.

Однополостный гиперболоид
Опр. 4. Однополостный гиперболоид – это поверхность, которая в
некоторой прямоугольной декартовой системе координат задается уравнением
x2 y 2 z 2
2 2 1.
2
a
b
c
Применим метод сечений.
Будем пересекать данную поверхность плоскостями z = h, || плоскости Oxy.
При заданном h линия, полученная в сечении, определяется в плоскости z = h (в
системе координат с началом в точке (0; 0; h) и осями, || Ox и Oy) уравнением
x2 y 2
h2
2 1 2 .
2
a
b
c
При h = 0 (в плоскости Oxy) получим эллипс с полуосями a и b.
x2
y2
При h ≠ 0 получим линию
1.
2
2
h
h
2
2
a 1 2 b 1 2
c
c
В сечении плоскостью Oyz (при x = 0) получается линия
y2 z2
2 1,
2
b
c
т. е. гипербола с полуосями b и c. Действительной осью
здесь является ось Oy (гипербола пересекает ось Oy в
точках b и –b), а мнимой – ось Oz.

7.

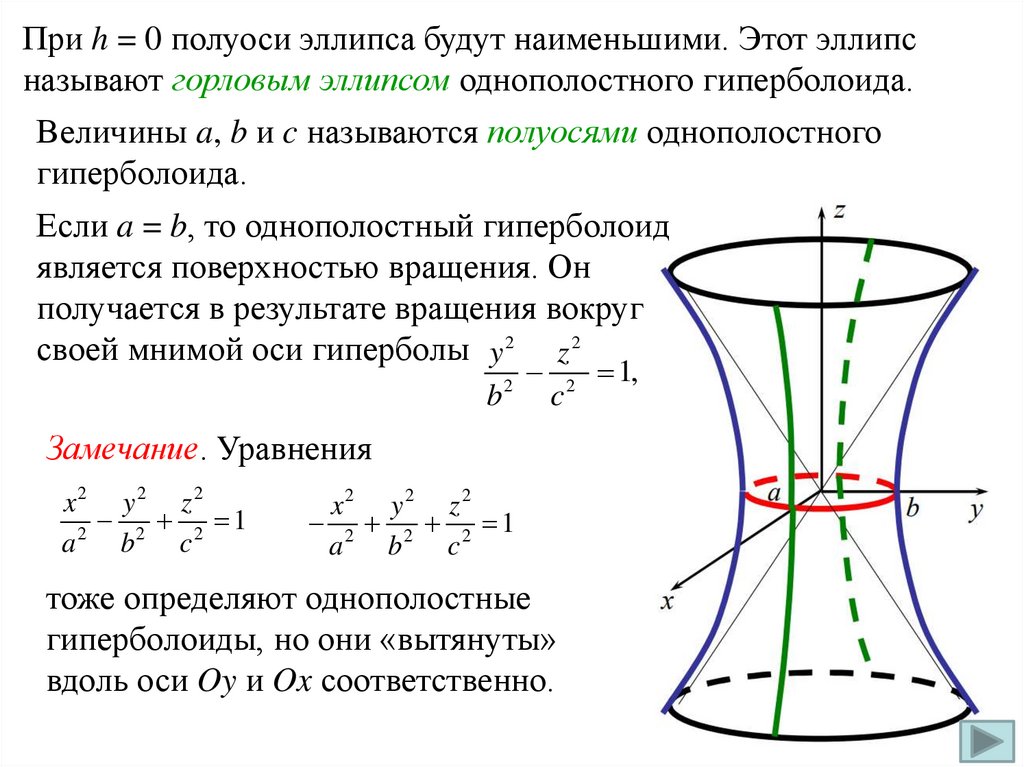
При h = 0 полуоси эллипса будут наименьшими. Этот эллипс
называют горловым эллипсом однополостного гиперболоида.
Величины a, b и c называются полуосями однополостного
гиперболоида.
Если a = b, то однополостный гиперболоид
является поверхностью вращения. Он
получается в результате вращения вокруг
своей мнимой оси гиперболы y 2 z 2
b
2
c
Замечание. Уравнения
x2 y 2 z 2
1
a 2 b2 c2
x2 y 2 z 2
2 2 2 1
a
b
c
тоже определяют однополостные
гиперболоиды, но они «вытянуты»
вдоль оси Oy и Ox соответственно.
2
1,

8.

Двуполостный гиперболоид
Опр. 5. Двуполостный гиперболоид – это поверхность, которая в некоторой
прямоугольной декартовой системе координат задается уравнением
x2 y 2 z 2
2 2 1.
2
a
b
c
Применим метод сечений.
Будем пересекать данную поверхность плоскостями z = h, || плоскости Oxy.
При заданном h линия, полученная в сечении, определяется в плоскости z = h (в
системе координат с началом в точке (0; 0; h) и осями, || Ox и Oy) уравнением
При |h| < c плоскость не пересекает гиперболоид.
При |h| = c получим в сечении точку.
2
2
x
y
При |h| > c получим эллипс
h
a 2 2 1
c
2
h
b 2 2 1
c
2
x 2 y 2 h2
2 2 1.
2
a
b
c
1.
В сечении плоскостью Oyz (при x = 0) получается линия
y2 z2
2 2 1,
b
c
т. е. гипербола с полуосями b и c. Действительной осью
здесь является ось Oz (гипербола пересекает ось Oz в
точках c и –c), а мнимой – ось Oy.

9.

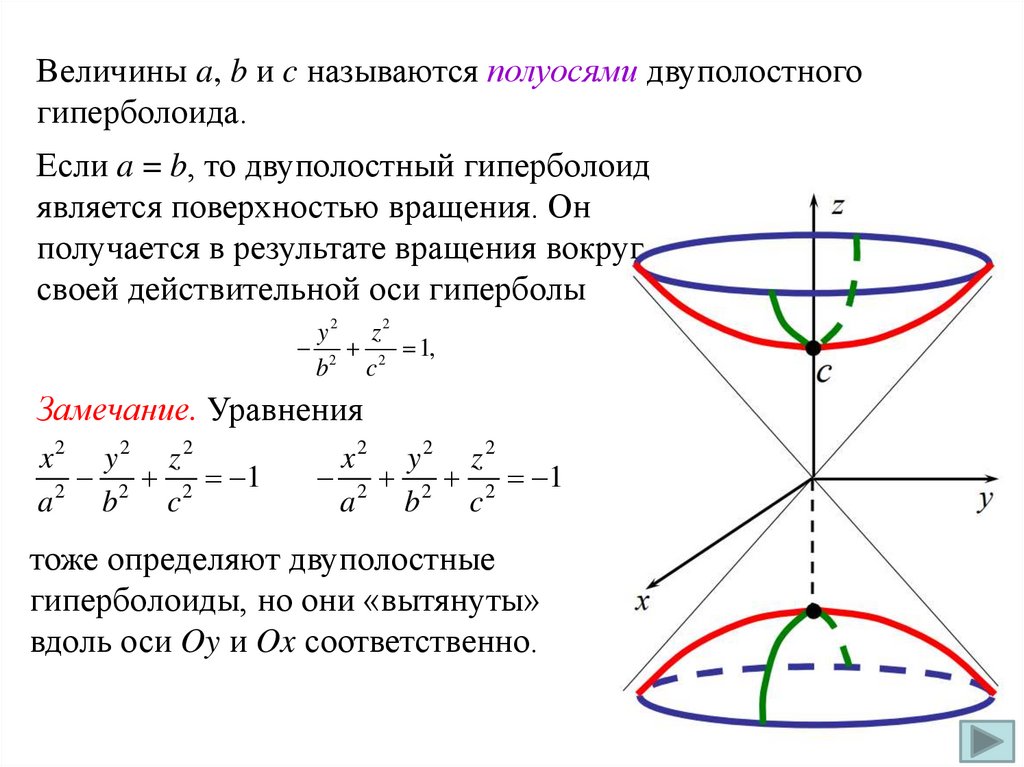
Величины a, b и c называются полуосями двуполостного
гиперболоида.
Если a = b, то двуполостный гиперболоид
является поверхностью вращения. Он
получается в результате вращения вокруг
своей действительной оси гиперболы
y2 z2
2 2 1,
b c
Замечание. Уравнения
x2 y 2 z 2
2 2 1
2
a
b
c
x2 y 2 z 2
2 2 2 1
a
b
c
тоже определяют двуполостные
гиперболоиды, но они «вытянуты»
вдоль оси Oy и Ox соответственно.

10.

Коническая поверхность
Опр. 6. Коническая поверхность – это поверхность, которая в некоторой
прямоугольной декартовой системе координат задается уравнением
x2 y 2 z 2
2 2 0.
2
a
b
c
Применим метод сечений.
Будем пересекать данную поверхность плоскостями z = h, || плоскости Oxy.
При заданном h линия, полученная в сечении, определяется в плоскости z = h (в
системе координат с началом в точке (0; 0; h) и осями, || Ox и Oy) уравнением
При h = 0 получим в сечении точку – начало координат.
2
2
x
y
При h ≠ 0 получим эллипс
2 2 1.
2 2
ah
bh
c2
c2
В сечении плоскостью Oyz (при x = 0) получается линия
y2 z2
2 0,
2
b
c
b
т. е. пара пересекающихся прямых y z.
c
x2 y 2 h2
2 2.
2
a
b
c

11.

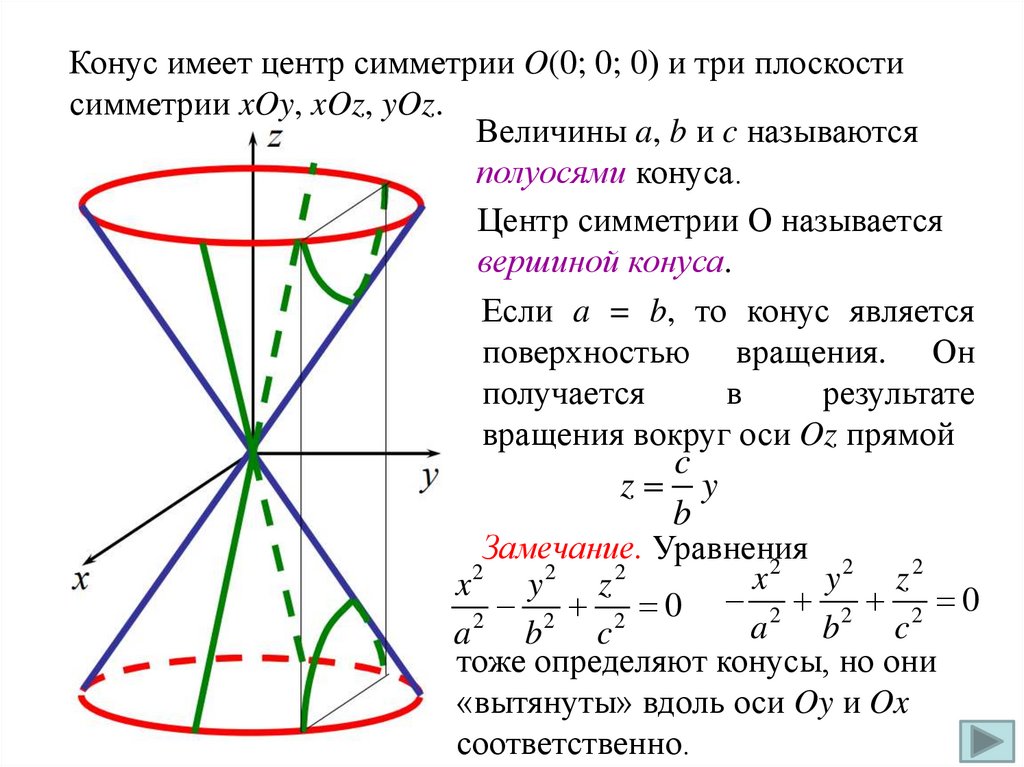
Конус имеет центр симметрии O(0; 0; 0) и три плоскости
симметрии xOy, xOz, yOz.
Величины a, b и c называются
полуосями конуса.
Центр симметрии O называется
вершиной конуса.
Если a = b, то конус является
поверхностью вращения. Он
получается
в
результате
вращения вокруг оси Oz прямой
c
z y
b
Замечание. Уравнения
2
2
2
2
2
x
y
z
x
y
z
2 2 0 2 2 2 0
2
a
b
c
a
b
c
тоже определяют конусы, но они
«вытянуты» вдоль оси Oy и Ox
соответственно.
2

12.

Эллиптический параболоид
Опр. 7. Эллиптический параболоид – это поверхность, которая в некоторой
прямоугольной декартовой системе координат задается уравнением
x2 y 2
2 z.
2
a
b
Исследуем форму этой поверхности методом сечений.
Рассмотрим сечения плоскостями z = h, параллельными плоскости Oxy:
При h < 0 пересечения нет.
При h = 0 получим в сечении точку – начало координат.
При h > 0 получим эллипс с полуосями a
увеличивающимися с возрастанием h.
h; b h,
В сечении плоскостью Oyz (при x = 0) получается
y2
парабола 2 z с вершиной в начале координат и осью
b
симметрии Oz.
x2 y 2
2 h.
2
a
b

13.

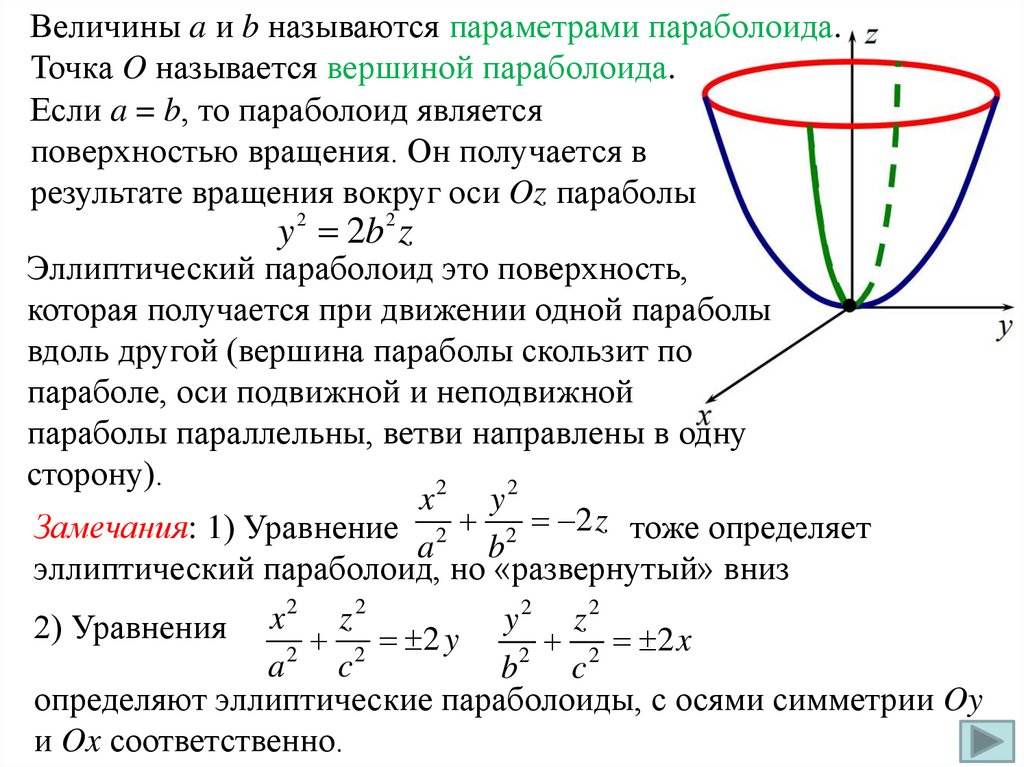
Величины a и b называются параметрами параболоида.
Точка O называется вершиной параболоида.
Если a = b, то параболоид является
поверхностью вращения. Он получается в
результате вращения вокруг оси Oz параболы
y 2 2b 2 z
Эллиптический параболоид это поверхность,
которая получается при движении одной параболы
вдоль другой (вершина параболы скользит по
параболе, оси подвижной и неподвижной
параболы параллельны, ветви направлены в одну
сторону).
x2 y 2
Замечания: 1) Уравнение 2 2 2 z тоже определяет
a
b
эллиптический параболоид, но «развернутый» вниз
2
2
2
2
x
z
y
z
2) Уравнения
2 2 y
2 2 x
2
2
a
c
b
c
определяют эллиптические параболоиды, с осями симметрии Oy
и Ox соответственно.

14.

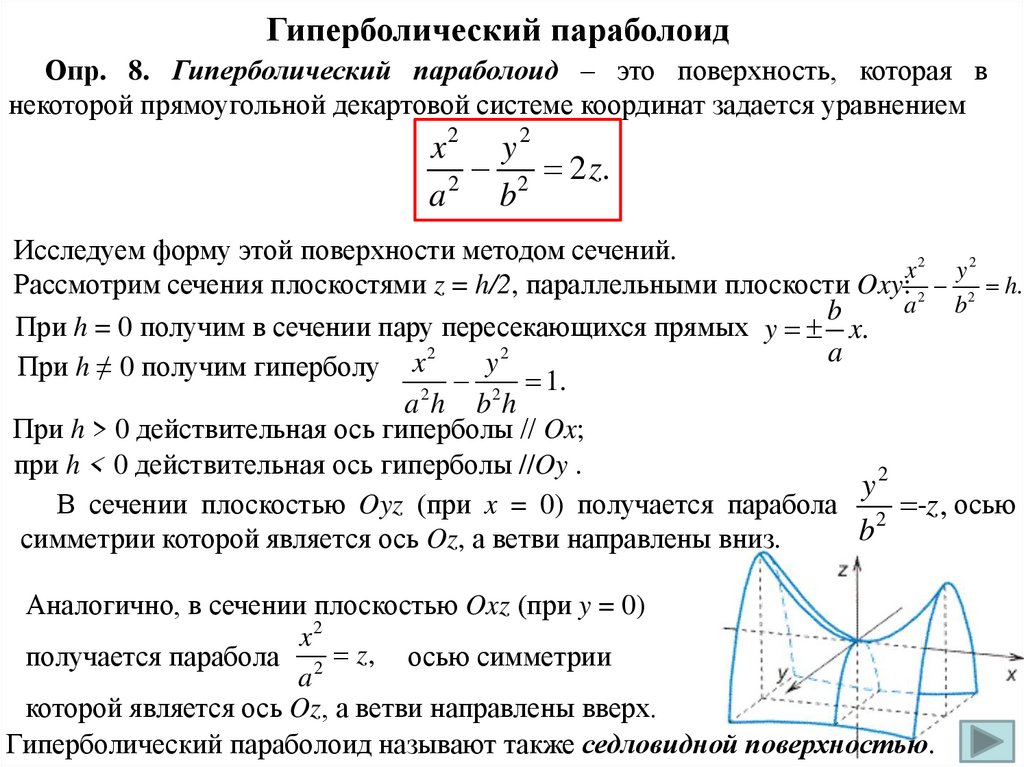
Гиперболический параболоид
Опр. 8. Гиперболический параболоид – это поверхность, которая в
некоторой прямоугольной декартовой системе координат задается уравнением
x2 y 2
2 2 z.
2
a
b
Исследуем форму этой поверхности методом сечений.
x2 y 2
Рассмотрим сечения плоскостями z = h/2, параллельными плоскости Oxy: 2 2 h.
a
b
b
При h = 0 получим в сечении пару пересекающихся прямых y x.
2
2
a
При h ≠ 0 получим гиперболу x y 1.
a 2h b2h
При h > 0 действительная ось гиперболы // Ox;
при h < 0 действительная ось гиперболы //Oy .
y2
В сечении плоскостью Oyz (при x = 0) получается парабола 2 -z , осью
b
симметрии которой является ось Oz, а ветви направлены вниз.
Аналогично, в сечении плоскостью Oxz (при y = 0)
x2
получается парабола 2 z , осью симметрии
a
которой является ось Oz, а ветви направлены вверх.
Гиперболический параболоид называют также седловидной поверхностью.

15.

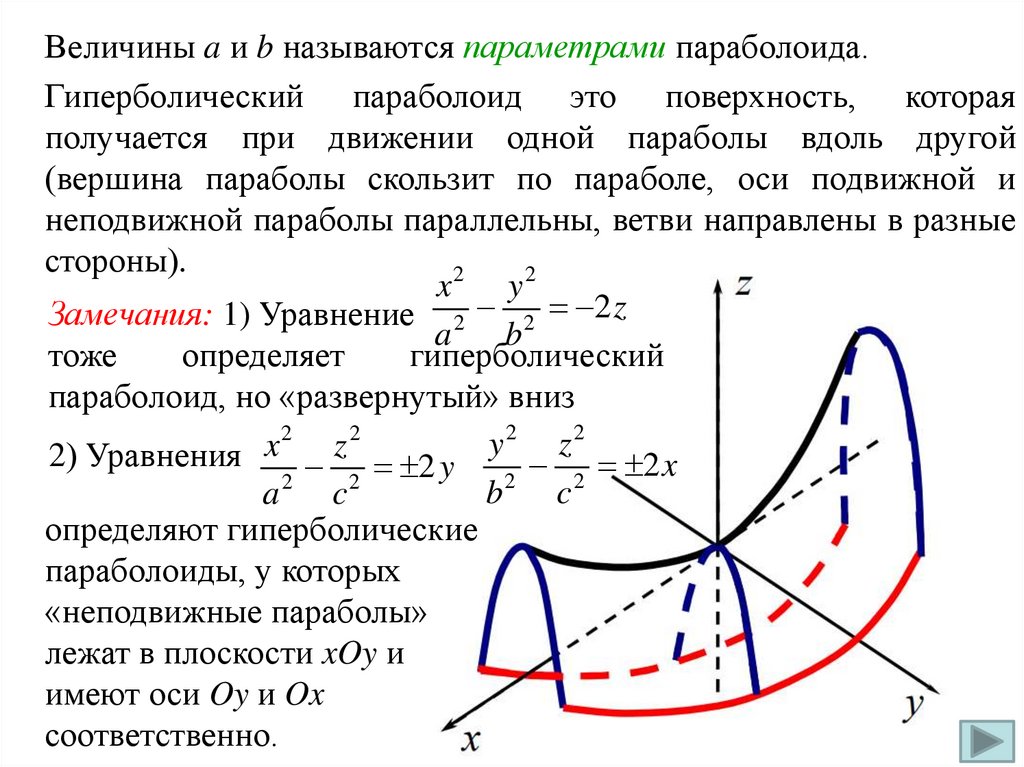
Величины a и b называются параметрами параболоида.
Гиперболический параболоид это поверхность, которая
получается при движении одной параболы вдоль другой
(вершина параболы скользит по параболе, оси подвижной и
неподвижной параболы параллельны, ветви направлены в разные
стороны).
x2 y 2
Замечания: 1) Уравнение 2 2 2 z
a
b
тоже
определяет
гиперболический
параболоид, но «развернутый» вниз
2
2
2
2
y
z
x
z
2) Уравнения
2 2 y 2 2 2 x
2
b
c
a
c
определяют гиперболические
параболоиды, у которых
«неподвижные параболы»
лежат в плоскости xOy и
имеют оси Oy и Ox
соответственно.

16.

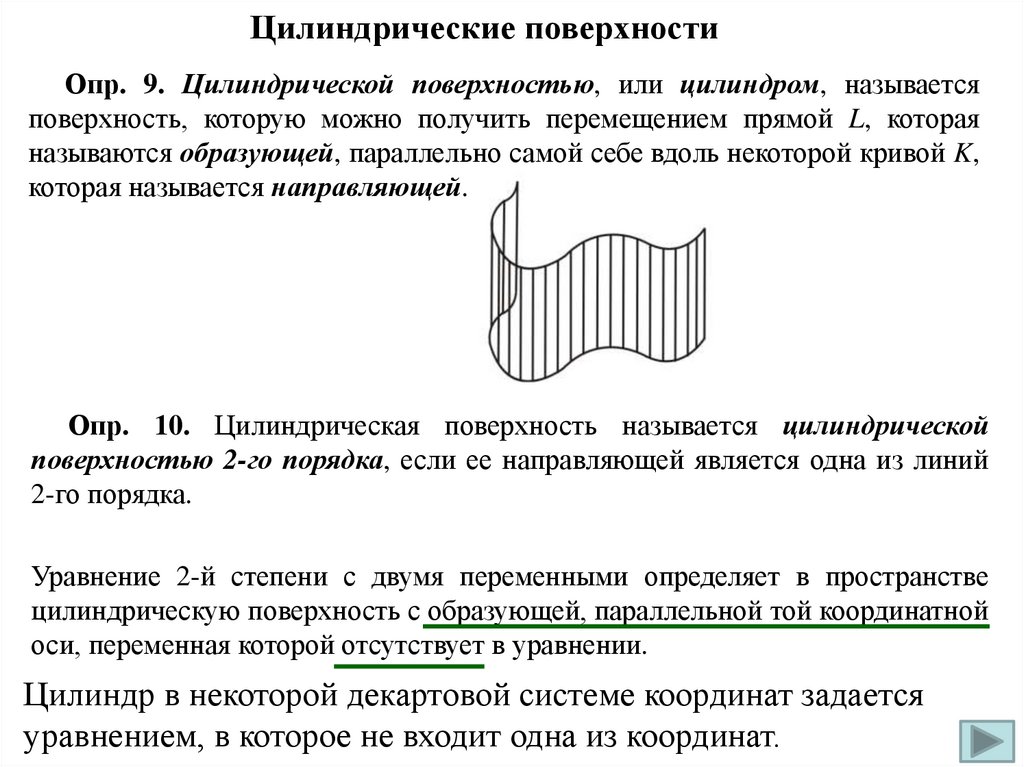
Цилиндрические поверхности
Опр. 9. Цилиндрической поверхностью, или цилиндром, называется
поверхность, которую можно получить перемещением прямой L, которая
называются образующей, параллельно самой себе вдоль некоторой кривой K,
которая называется направляющей.
Опр. 10. Цилиндрическая поверхность называется цилиндрической
поверхностью 2-го порядка, если ее направляющей является одна из линий
2-го порядка.
Уравнение 2-й степени с двумя переменными определяет в пространстве
цилиндрическую поверхность с образующей, параллельной той координатной
оси, переменная которой отсутствует в уравнении.
Цилиндр в некоторой декартовой системе координат задается
уравнением, в которое не входит одна из координат.

17.

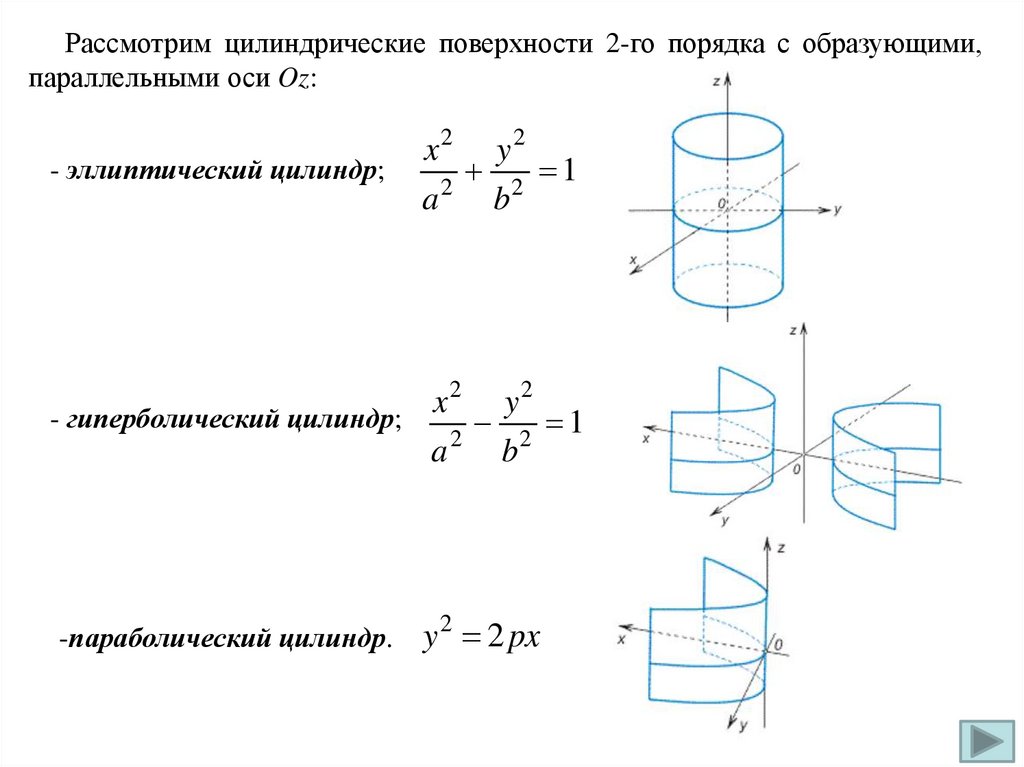
Рассмотрим цилиндрические поверхности 2-го порядка с образующими,
параллельными оси Oz:
- эллиптический цилиндр;
x2 y2
2 1
2
a
b
2
2
x
y
- гиперболический цилиндр;
2 1
2
a
b
-параболический цилиндр.
y 2 2 px

18.

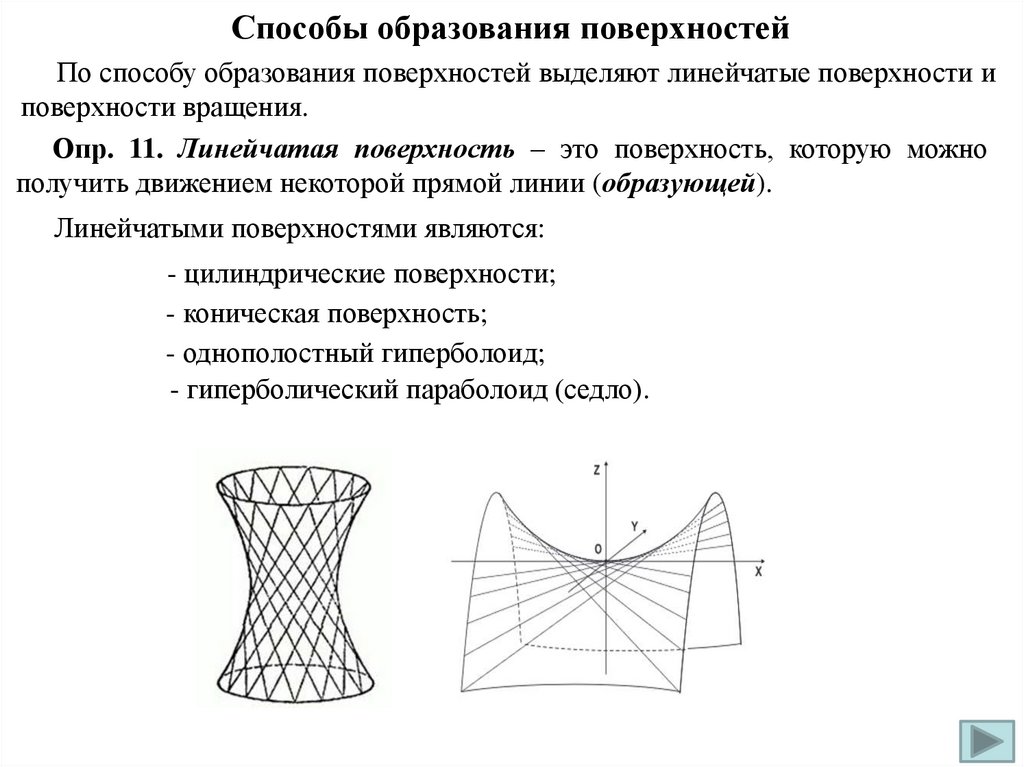
Способы образования поверхностей
По способу образования поверхностей выделяют линейчатые поверхности и
поверхности вращения.
Опр. 11. Линейчатая поверхность – это поверхность, которую можно
получить движением некоторой прямой линии (образующей).
Линейчатыми поверхностями являются:
- цилиндрические поверхности;
- коническая поверхность;
- однополостный гиперболоид;
- гиперболический параболоид (седло).

19.

Опр. 12. Поверхность вращения – это поверхность, образованная
вращением некоторой плоской кривой вокруг оси, лежащей в ее плоскости.
Поверхность, полученная вращением вокруг оси Oz, имеет уравнение
F(x2 + y2; z) = 0.
Например,
x2 y 2 z 2
2 1
2
a
c
– эллипсоид вращения;
x2 y 2 z 2
x2 y 2 z 2
2 1;
2 1 – однополостный и двуполостный
2
a2
c
a
c
гиперболоиды вращения;
x2 y 2 a 2 z
x2 y 2 z 2
2 0
2
a
c
x2 y 2 a2
– параболоид
параболоид);
вращения
– круговой конус;
– круговой цилиндр.
Упражнение. Построить поверхности:
(круговой

20.

21.

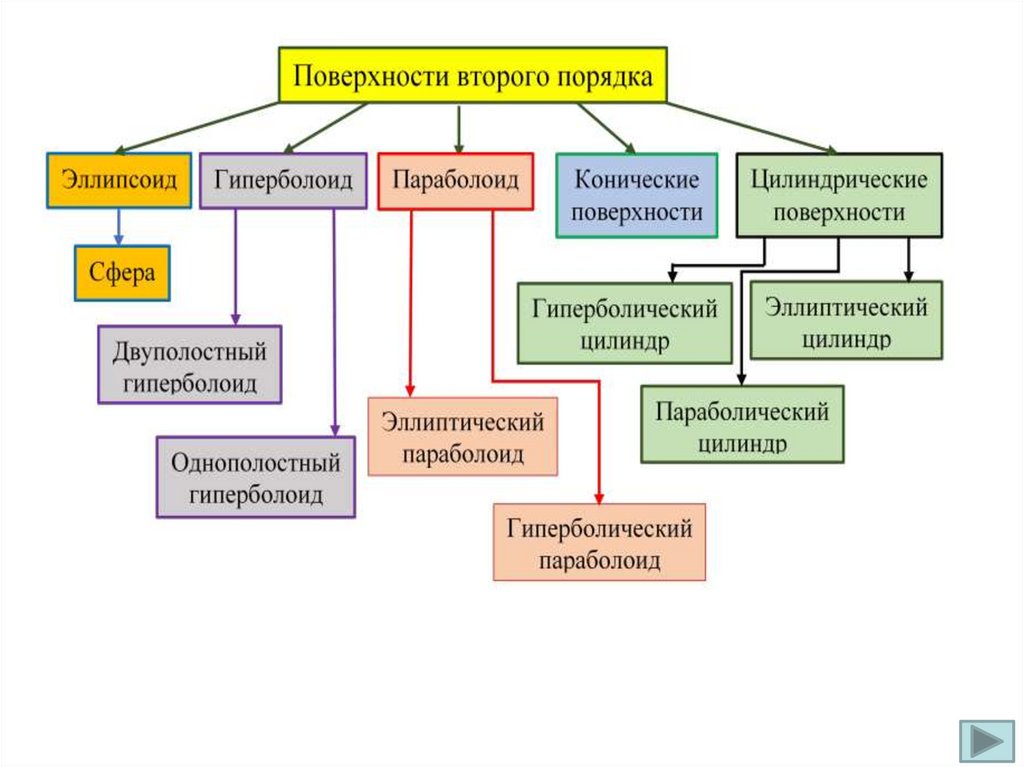
Классификация поверхностей второго порядка
эллиптические
x2 y 2 z 2
2 2 1 эллипсоид,
2
a
b
c
x2 y 2 z 2
2 2 1 – мнимый эллипсоид;
2
a
b
c
гиперболические
x2 y 2 z 2
2 2 1 – однополостный гиперболоид,
2
a
b
c
x2 y 2 z 2
2 2 1 – двуполостный гиперболоид;
2
a
b
c
параболические x 2 y 2
2 2 z – эллиптический параболоид,
2
a
b
x2 y 2
2 2 z – гиперболический параболоид.
2
a
b

22.

цилиндрические
x2 y2
2 1 – эллиптический цилиндр,
2
a
b
x2 y 2
2 1 – мнимый эллиптический цилиндр,
2
a
b
x2 y 2
2 1 – гиперболический цилиндр,
2
a
b
y 2 2 px – параболический цилиндр;
конические
x2 y 2 z 2
2 2 0 – конус,
2
a
b
c
x2 y 2 z 2
2 2 0 – мнимый конус.
2
a
b
c

23.

Распадающиеся вырождающиеся поверхности
x2 y 2
2 0 – пара пересекающихся плоскостей,
2
a
b
x2 y 2
2 0 – пара мнимых пересекающихся плоскостей,
2
a
b
x 2 a 2 – пара параллельных плоскостей,
x 2 a 2 – пара мнимых параллельных плоскостей,
x 2 0 – пара совпадающих плоскостей.