Tochki_extremuma_funktsii

1. Точки экстремума функции

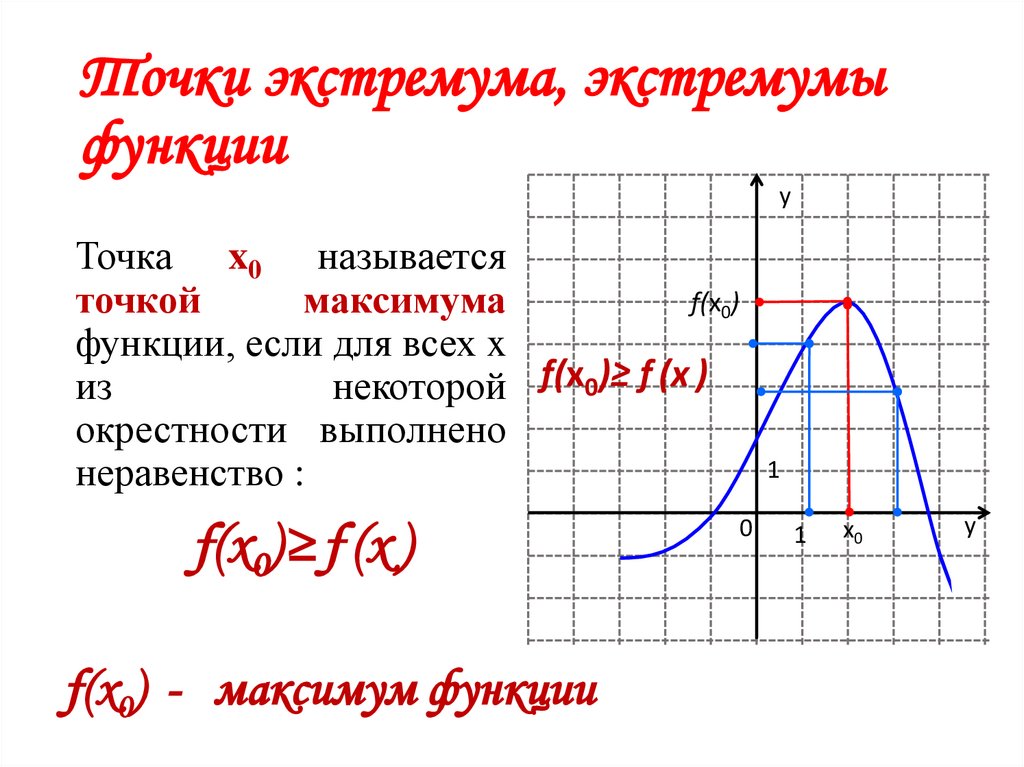
2. Точки экстремума, экстремумы функции

y
Точка x0 называется
f(x0)
точкой
максимума
функции, если для всех x
из
некоторой f(x0)≥ f (х )
окрестности выполнено
неравенство :
f(x0)≥ f (х )
f(x0) - максимум функции
1
0
1
x0
y

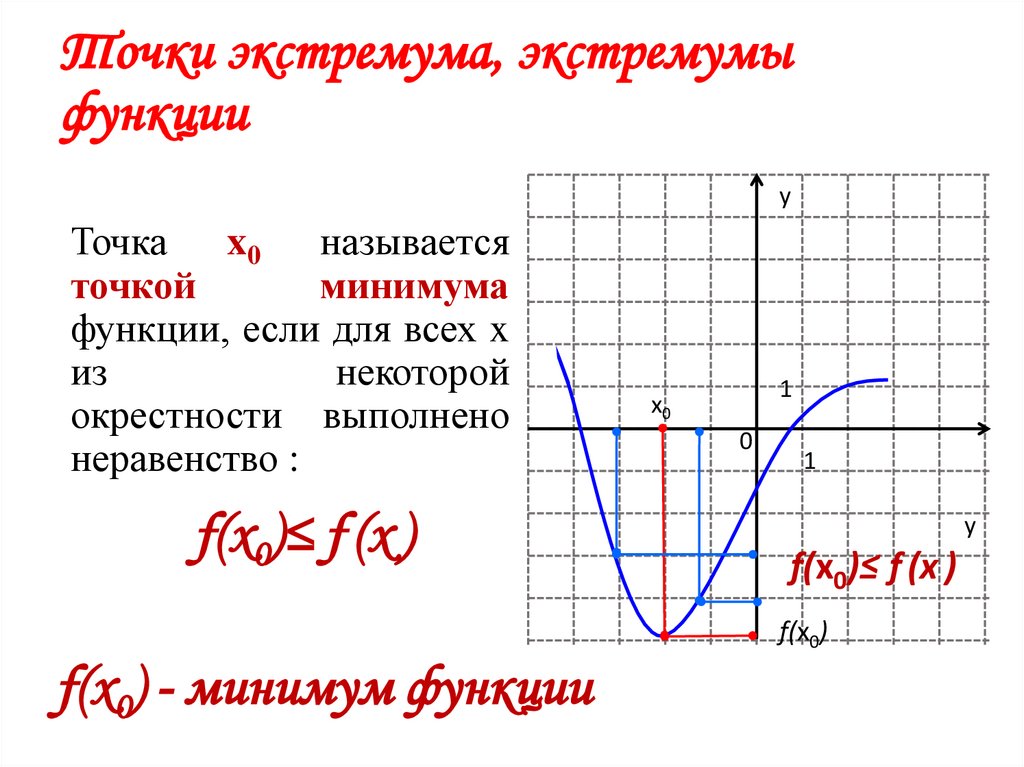
3. Точки экстремума, экстремумы функции

y
Точка x0 называется
точкой
минимума
функции, если для всех x
из
некоторой
окрестности выполнено
неравенство :
f(x0)≤ f (х )
1
x0
0
1
y
f(x0)≤ f (х )
f(x0)
f(x0) - минимум функции

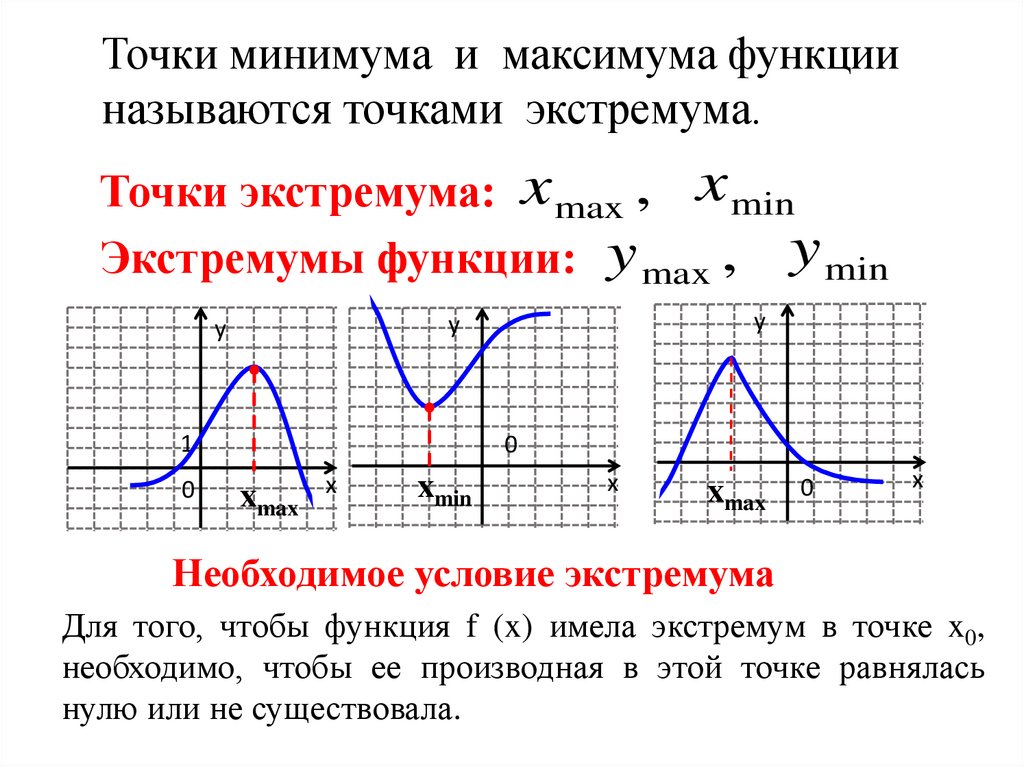
4.

Точки минимума и максимума функции
называются точками экстремума.
Точки экстремума: x max , x min
Экстремумы функции: y max , y min
1
0
y
y
y
0
xmax
x
xmin
x
xmax
0
x
Необходимое условие экстремума
Для того, чтобы функция f (x) имела экстремум в точке x0,
необходимо, чтобы ее производная в этой точке равнялась
нулю или не существовала.

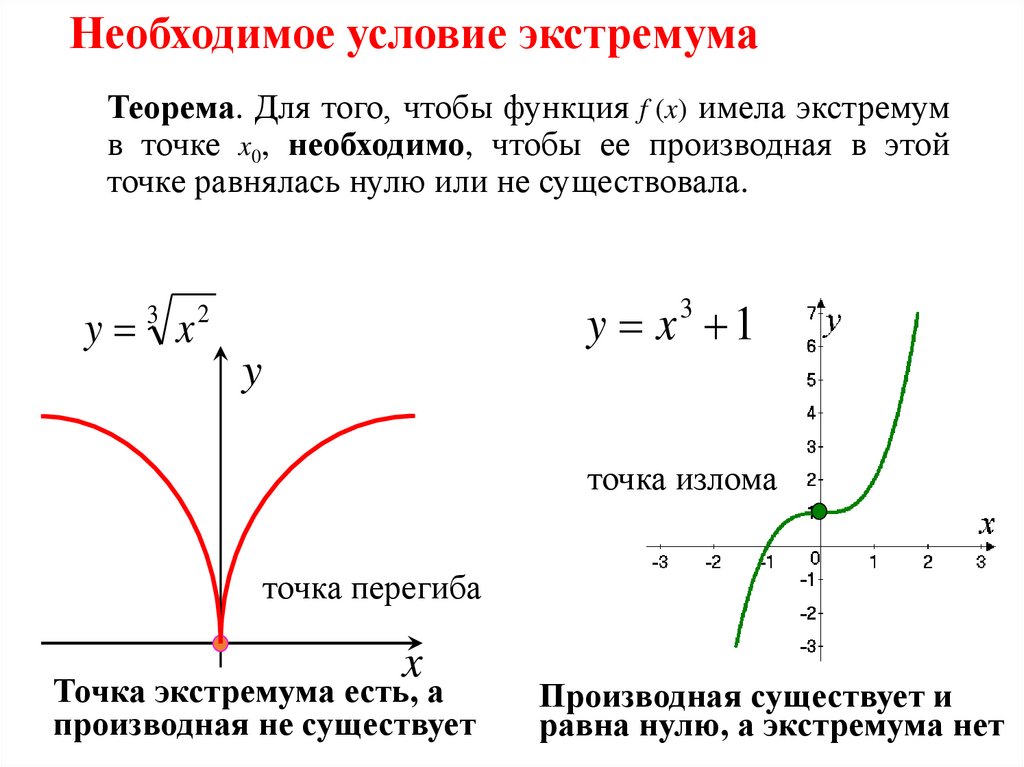
5. Необходимое условие экстремума

Теорема. Для того, чтобы функция f (x) имела экстремум
в точке x0, необходимо, чтобы ее производная в этой
точке равнялась нулю или не существовала.
y x
3
y x 1
3
2
y
точка излома
точка перегиба
x
Точка экстремума есть, а
производная не существует
Производная существует и
равна нулю, а экстремума нет

6.

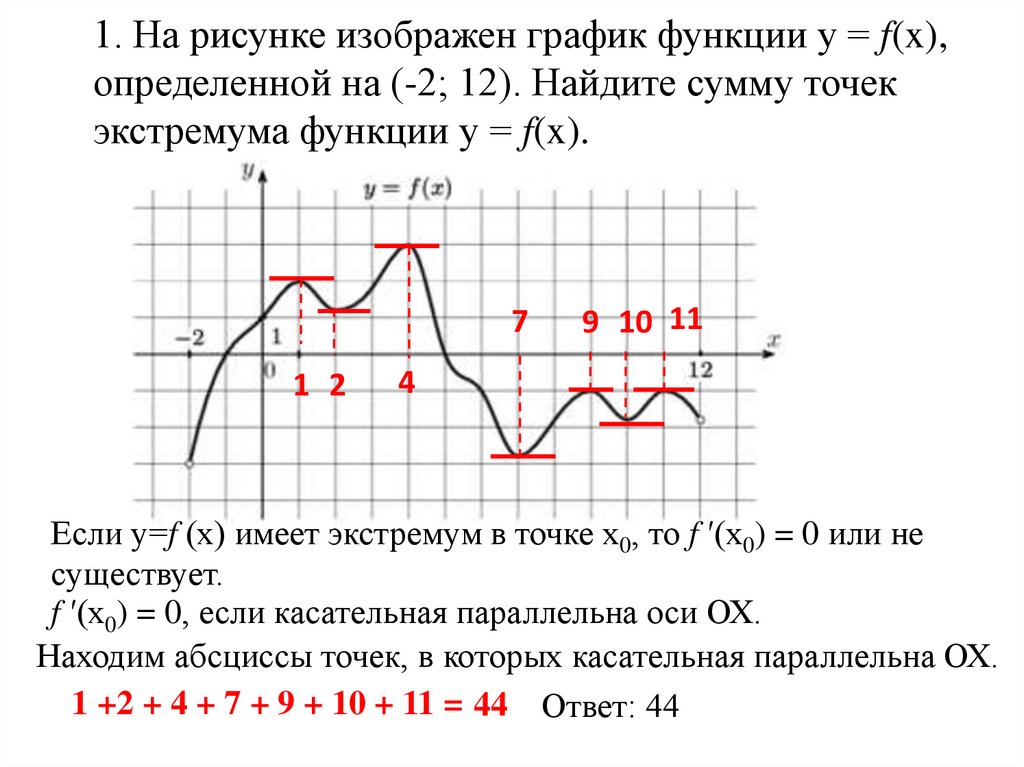
1. На рисунке изображен график функции у = f(x),
определенной на (-2; 12). Найдите сумму точек
экстремума функции у = f(x).
7
1 2
9 10 11
4
Если у=f (x) имеет экстремум в точке x0, то f ′(х0) = 0 или не
существует.
f ′(х0) = 0, если касательная параллельна оси ОХ.
Находим абсциссы точек, в которых касательная параллельна ОХ.
1 +2 + 4 + 7 + 9 + 10 + 11 = 44 Ответ: 44

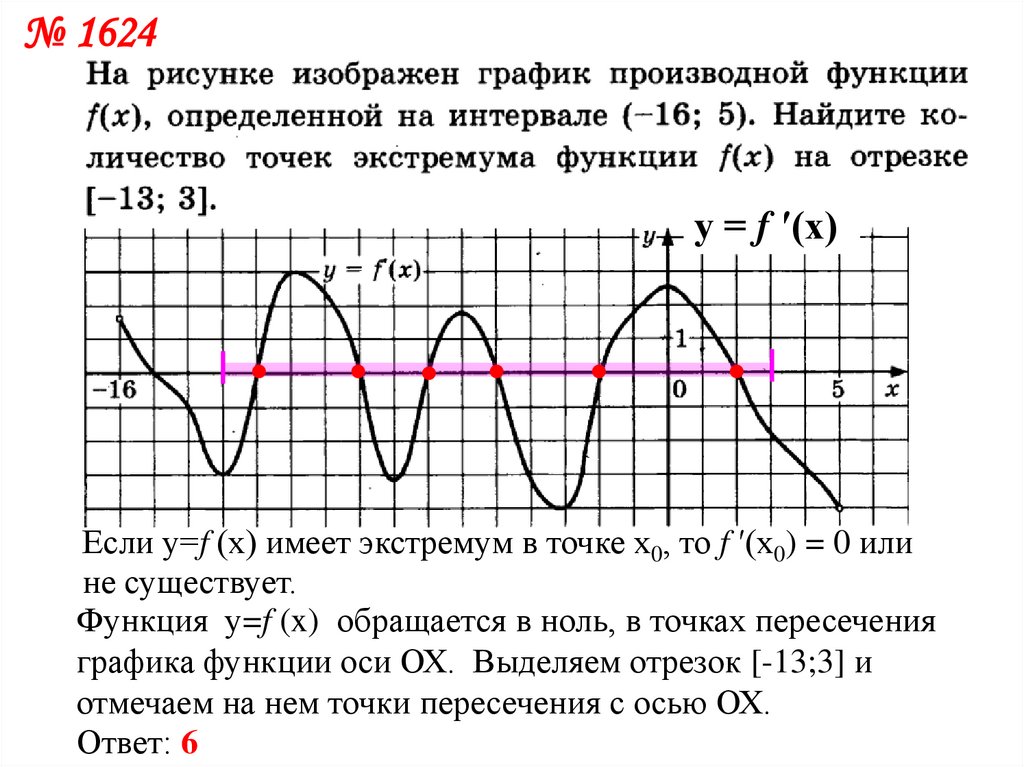
7.

№ 1624
у = f ′(x)
Если у=f (x) имеет экстремум в точке x0, то f ′(х0) = 0 или
не существует.
Функция у=f (x) обращается в ноль, в точках пересечения
графика функции оси ОХ. Выделяем отрезок [-13;3] и
отмечаем на нем точки пересечения с осью ОХ.
Ответ: 6

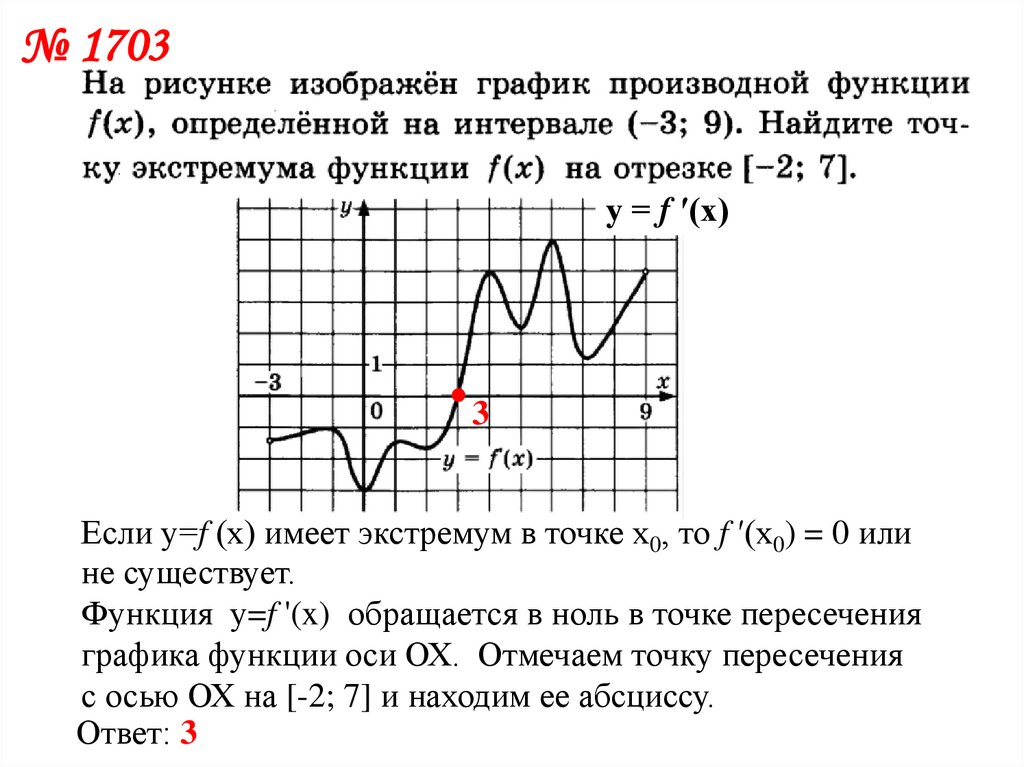
8.

№ 1703
у = f ′(x)
3
Если у=f (x) имеет экстремум в точке x0, то f ′(х0) = 0 или
не существует.
Функция у=f '(x) обращается в ноль в точке пересечения
графика функции оси ОХ. Отмечаем точку пересечения
с осью ОХ на [-2; 7] и находим ее абсциссу.
Ответ: 3

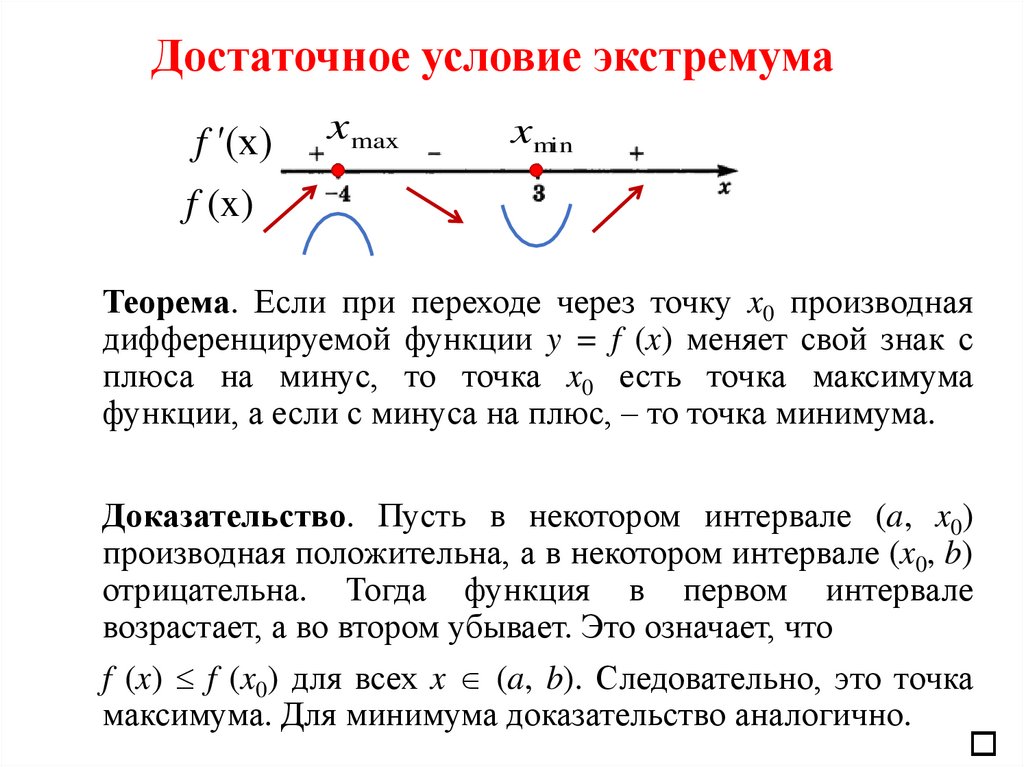
9. Достаточное условие экстремума

f ′(x)
x max
xmin
f (x)
Теорема. Если при переходе через точку x0 производная
дифференцируемой функции y = f (x) меняет свой знак с
плюса на минус, то точка x0 есть точка максимума
функции, а если с минуса на плюс, – то точка минимума.
Доказательство. Пусть в некотором интервале (a, x0)
производная положительна, а в некотором интервале (x0, b)
отрицательна. Тогда функция в первом интервале
возрастает, а во втором убывает. Это означает, что
f (x) f (x0) для всех x (a, b). Следовательно, это точка
максимума. Для минимума доказательство аналогично.

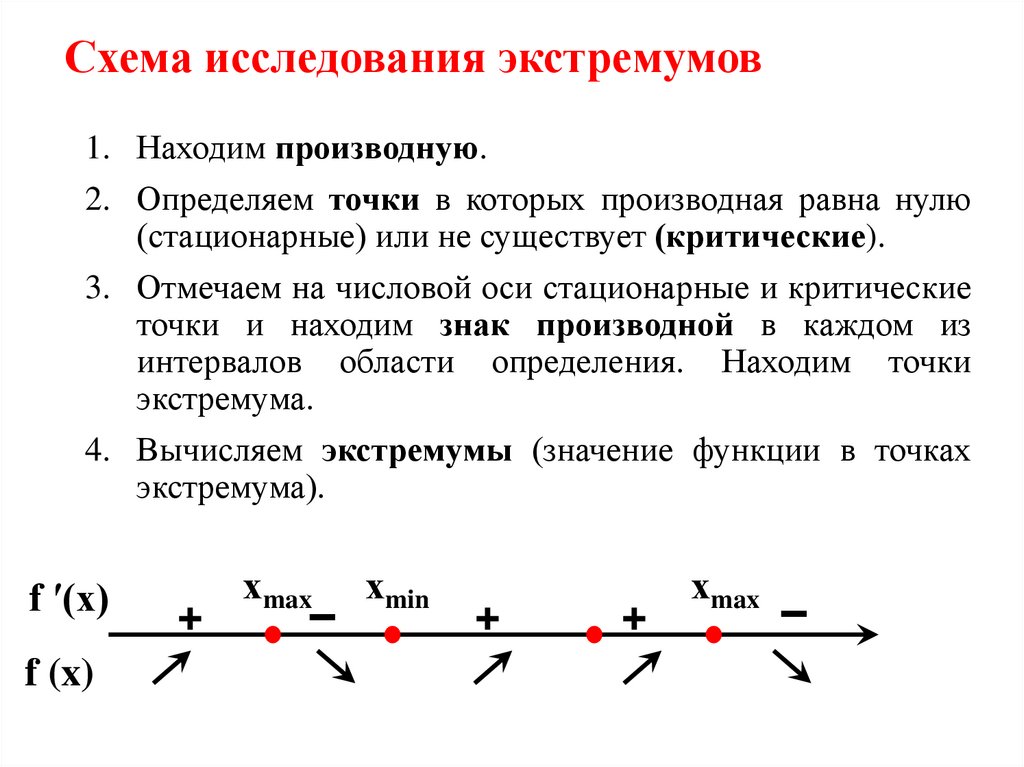
10. Схема исследования экстремумов

1. Находим производную.
2. Определяем точки в которых производная равна нулю
(стационарные) или не существует (критические).
3. Отмечаем на числовой оси стационарные и критические
точки и находим знак производной в каждом из
интервалов области определения. Находим точки
экстремума.
4. Вычисляем экстремумы (значение функции в точках
экстремума).
f ′(x)
f (x)
+
хmax
–
хmin
+
+
хmax
–

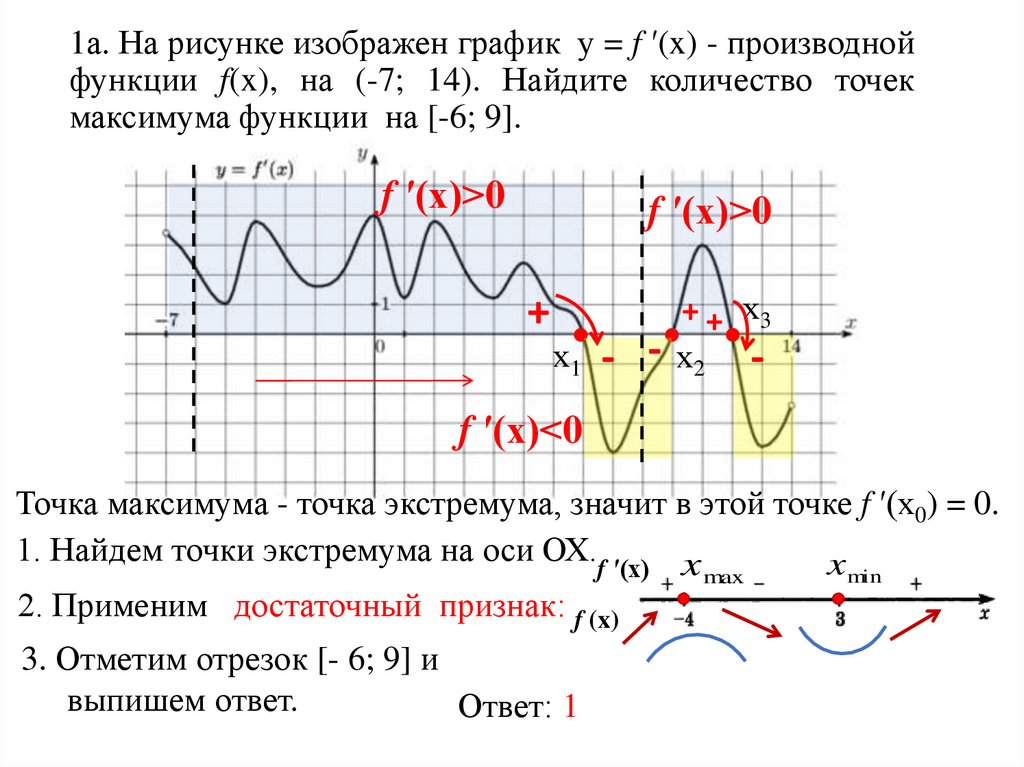
11.

1а. На рисунке изображен график у = f ′(x) - производной
функции f(x), на (-7; 14). Найдите количество точек
максимума функции на [-6; 9].
f ′(x)>0
f ′(x)>0
+
х1 -
+ + х3
- х2 -
f ′(x)<0
Точка максимума - точка экстремума, значит в этой точке f ′(x0) = 0.
1. Найдем точки экстремума на оси ОХ.f ′(x) x
x
2. Применим достаточный признак: f (x)
3. Отметим отрезок [- 6; 9] и
выпишем ответ.
Ответ: 1
max
min

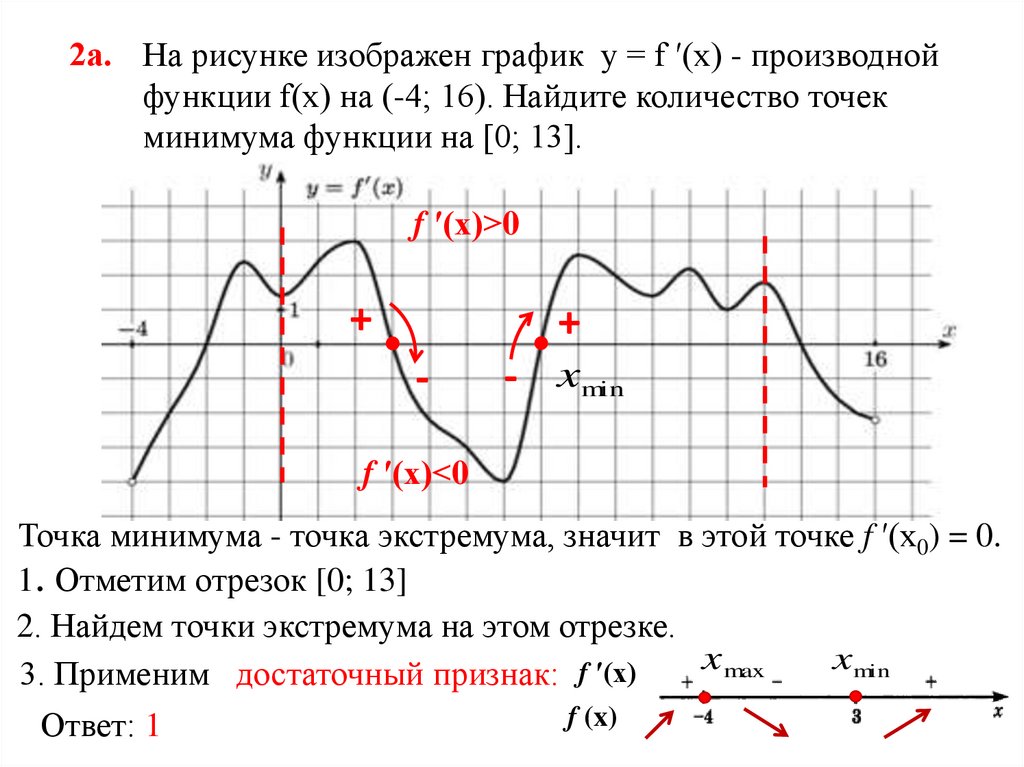
12.

2а. На рисунке изображен график у = f ′(x) - производной
функции f(x) на (-4; 16). Найдите количество точек
минимума функции на [0; 13].
f ′(x)>0
+
+
-
- xmin
f ′(x)<0
Точка минимума - точка экстремума, значит в этой точке f ′(x0) = 0.
1. Отметим отрезок [0; 13]
2. Найдем точки экстремума на этом отрезке.
x max
xmin
3. Применим достаточный признак: f ′(x)
f (x)
Ответ: 1

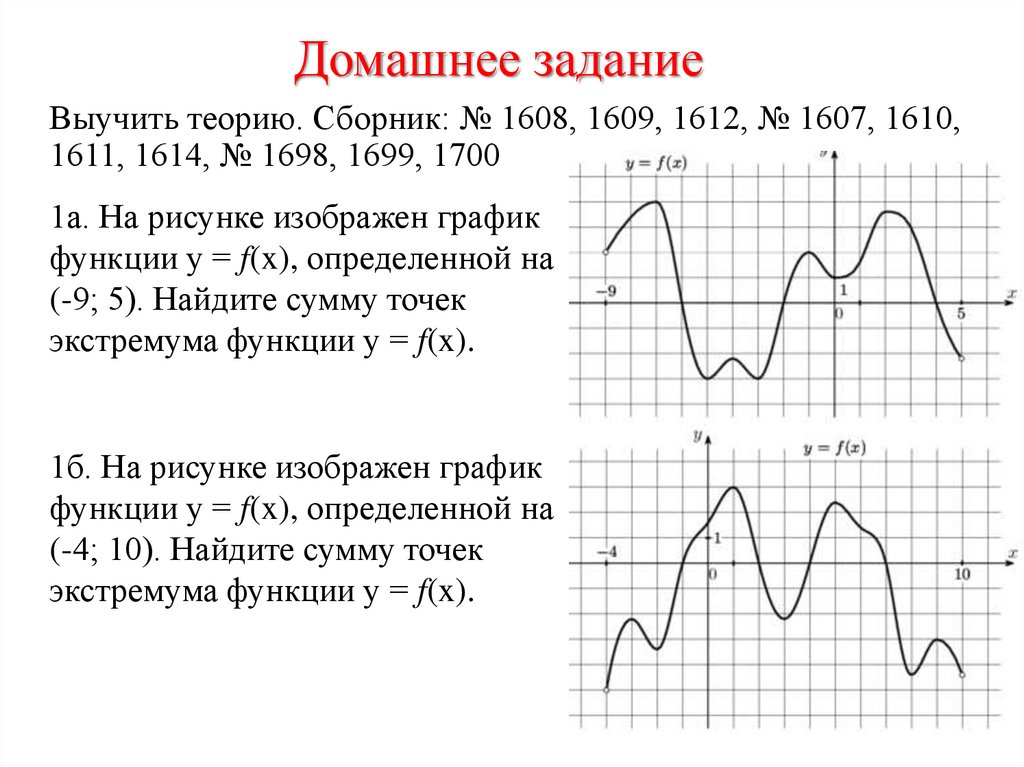
13. Домашнее задание

Выучить теорию. Сборник: № 1608, 1609, 1612, № 1607, 1610,
1611, 1614, № 1698, 1699, 1700
1а. На рисунке изображен график
функции у = f(x), определенной на
(-9; 5). Найдите сумму точек
экстремума функции у = f(x).
1б. На рисунке изображен график
функции у = f(x), определенной на
(-4; 10). Найдите сумму точек
экстремума функции у = f(x).

14.

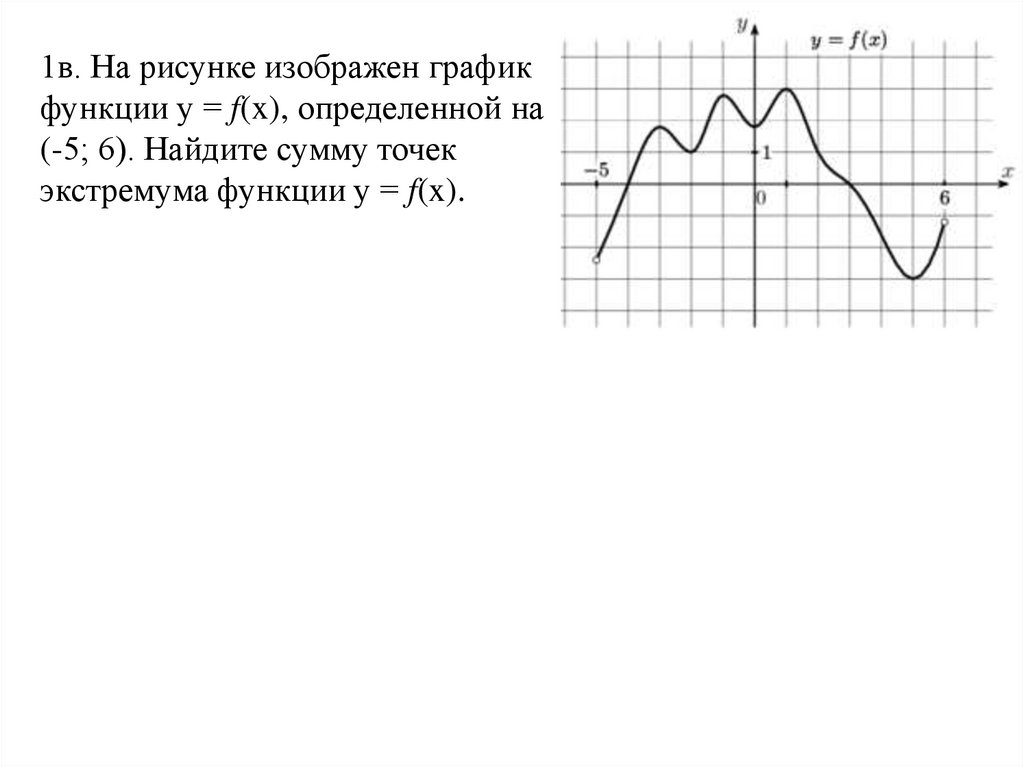
1в. На рисунке изображен график
функции у = f(x), определенной на
(-5; 6). Найдите сумму точек
экстремума функции у = f(x).