17_kvadr_nerav4

1. КВАДРАТИЧНАЯ ФУНКЦИЯ

Сенина Г.Н., Сенин В.Г., МБОУ «СОШ №4», г. Корсаков
Квадратные неравенства (часть 4)
Домашнее задание
У: с.118-119 – читать; ВИЗ(1-3); № 295(а, б); 296(а, б).
Метапредмет – Знак

2. Цель нашего урока

Вы узнаете
• как решать неравенства с опорой
на схематический график
квадратичной функции;
• как заменять неравенство
равносильным ему с
положительным коэффициентом
при х2;
Анализируя положение графика
функции y = ax2 + bx + с
относительно оси х мы, по сути,
находим множества решений
неравенств ax2 + bx + с > 0
или ax2 + bx + с < 0,
где а ≠ 0.
целеполагание

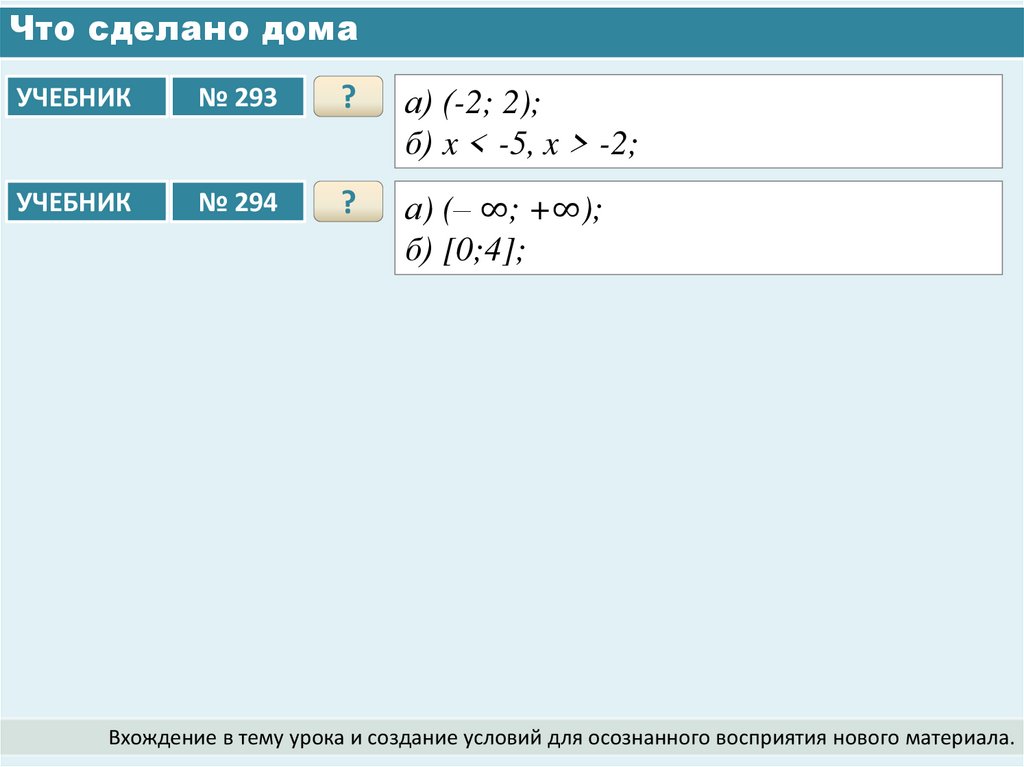
3. Что сделано дома

УЧЕБНИК
№ 293
?
а) (-2; 2);
б) x < -5, x > -2;
УЧЕБНИК
№ 294
?
а) (– ∞; +∞);
б) [0;4];
Вхождение в тему урока и создание условий для осознанного восприятия нового материала.

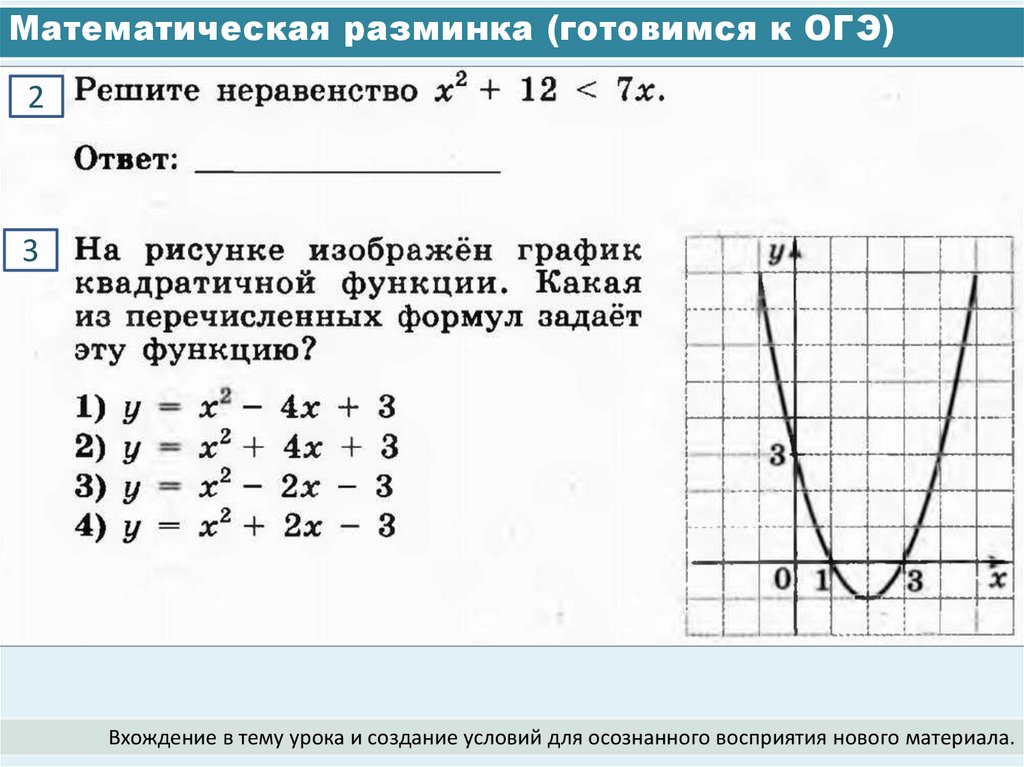
4. Математическая разминка (готовимся к ОГЭ)

1
Вхождение в тему урока и создание условий для осознанного восприятия нового материала.

5. Математическая разминка (готовимся к ОГЭ)

2
3
Вхождение в тему урока и создание условий для осознанного восприятия нового материала.

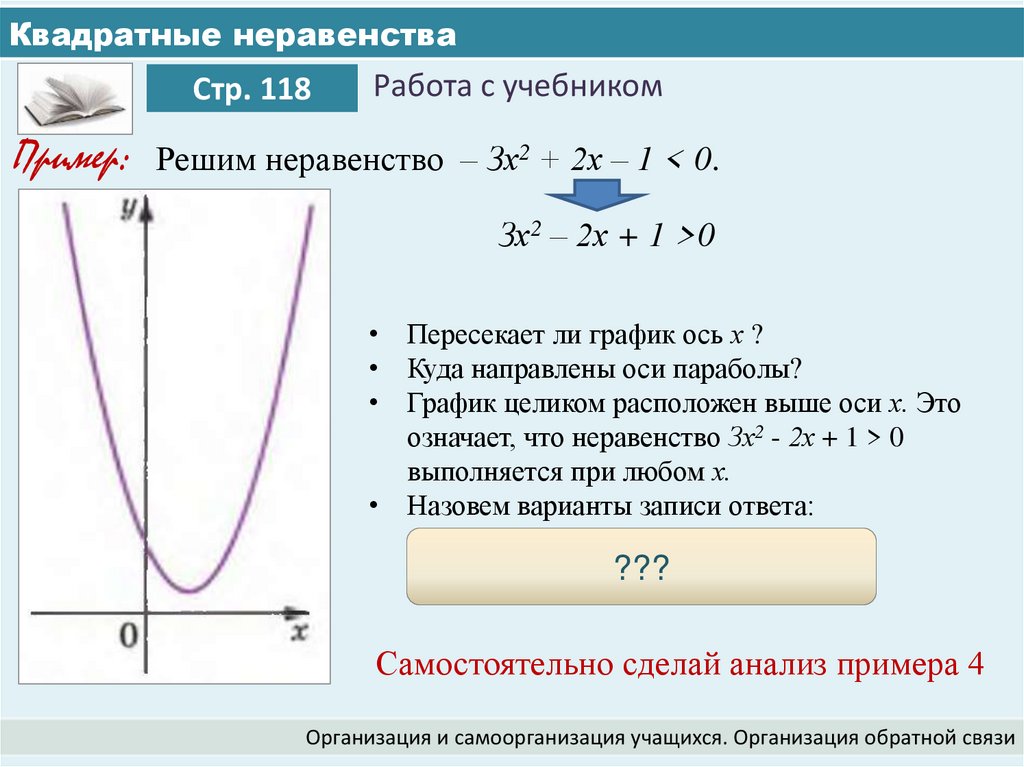
6. Квадратные неравенства

Стр. 118
Работа с учебником
Пример: Решим неравенство – Зх2 + 2х – 1 < 0.
Зх2 – 2х + 1 >0
• Пересекает ли график ось х ?
• Куда направлены оси параболы?
• График целиком расположен выше оси х. Это
означает, что неравенство Зх2 - 2х + 1 > 0
выполняется при любом х.
• Назовем варианты записи ответа:
Ответ: х – любое число.
??? ( – ∞ ; + ∞ ).)
(Ответ в другой форме:
Самостоятельно сделай анализ примера 4
Организация и самоорганизация учащихся. Организация обратной связи

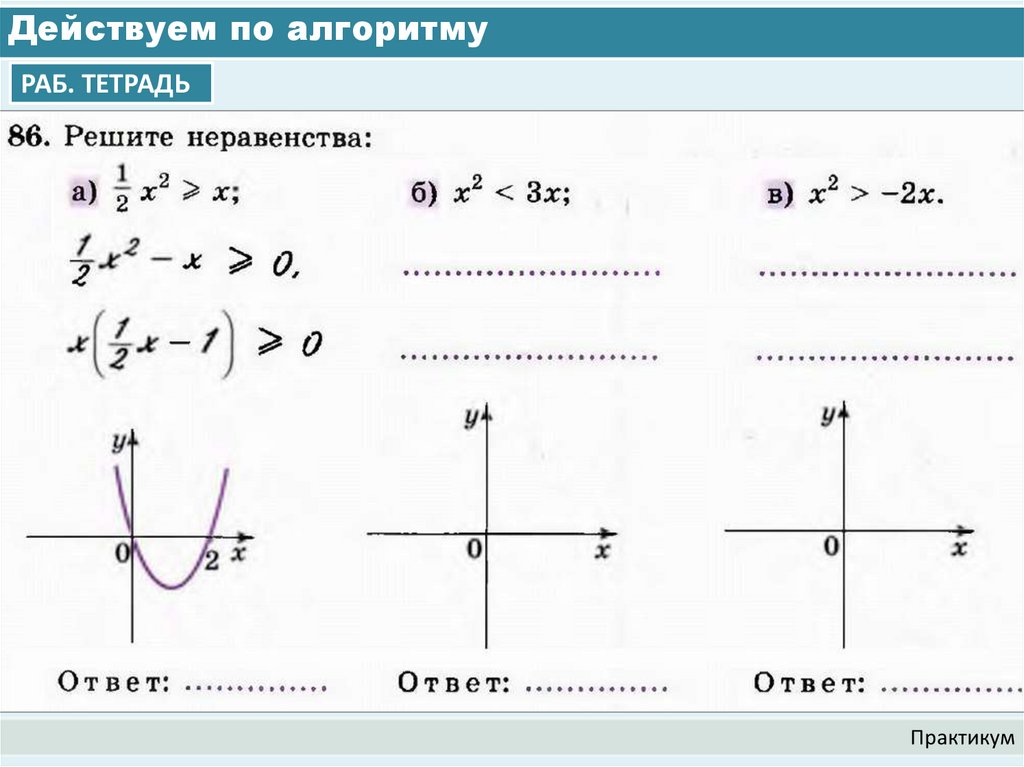
7. Действуем по алгоритму

РАБ. ТЕТРАДЬ
Практикум

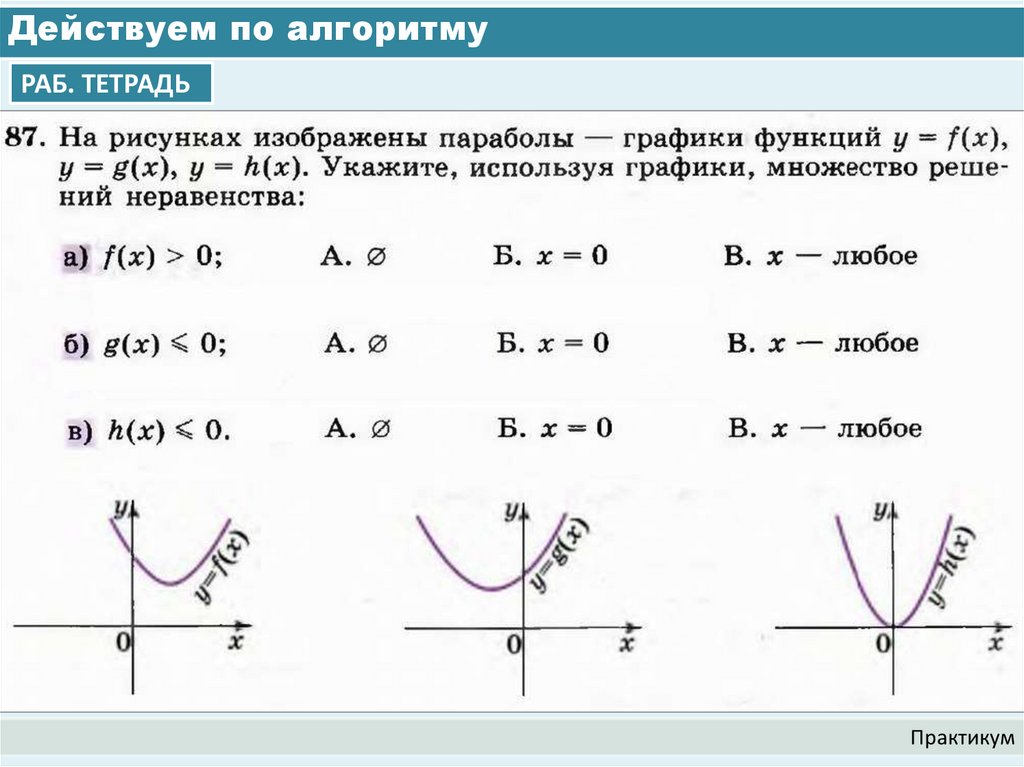
8. Действуем по алгоритму

РАБ. ТЕТРАДЬ
Практикум

9. Квадратные неравенства

УЧЕБНИК
в) ∅; д) ( –∞;+∞ ); з) x < 0, x >0;
д) [0;1]; и) x ≤-3, x≥3; к) (-10; 10); м) (-8; 8);
?
?
Практикум

10. Квадратные неравенства

УЧЕБНИК
ПРОДВИНУТЫМ
(0,25; 1);
?
?
а) x <5, x>10; г) (-7; -6);
(0; -1+ 3);
?
Практикум

11. Самостоятельная работа

Проверка полученных результатов. Коррекция

12. Пофилософствуем…

Что нужно, чтобы быть наверняка лучше других на ЕГЭ и быть в конечном
итоге… более счастливым?
НАБИТЬ РУКУ, РЕШАЯ ЗАДАЧИ ПО ЭТОЙ ТЕМЕ.
На экзамене у тебя не будут спрашивать теорию.
Тебе нужно будет решать задачи на время.
И, если ты не решал их (МНОГО!), ты обязательно где-нибудь глупо
ошибешься или просто не успеешь.
Это как в спорте - нужно много раз повторить, чтобы выиграть наверняка.
Найди где хочешь сборник, обязательно с решениями, подробным
разбором и решай, решай, решай!
И в заключение...
Если эти задачи тебе не нравятся, найди другие. Только не
останавливайся на теории.
“Понял” и “Умею решать” - это совершенно разные навыки. Тебе нужны
оба.
Найди задачи и решай!
Удачи!
Подведение итогов, рефлексия, домашнее задание.