6_Vektor_Deystvia_nad_vektorami

1. Векторная алгебра

2. Векторная алгебра

Понятие вектора
Длина вектора
Коллинеарные вектора
- Сонаправленные вектора
- Противоположно направленные вектора
Равенство векторов
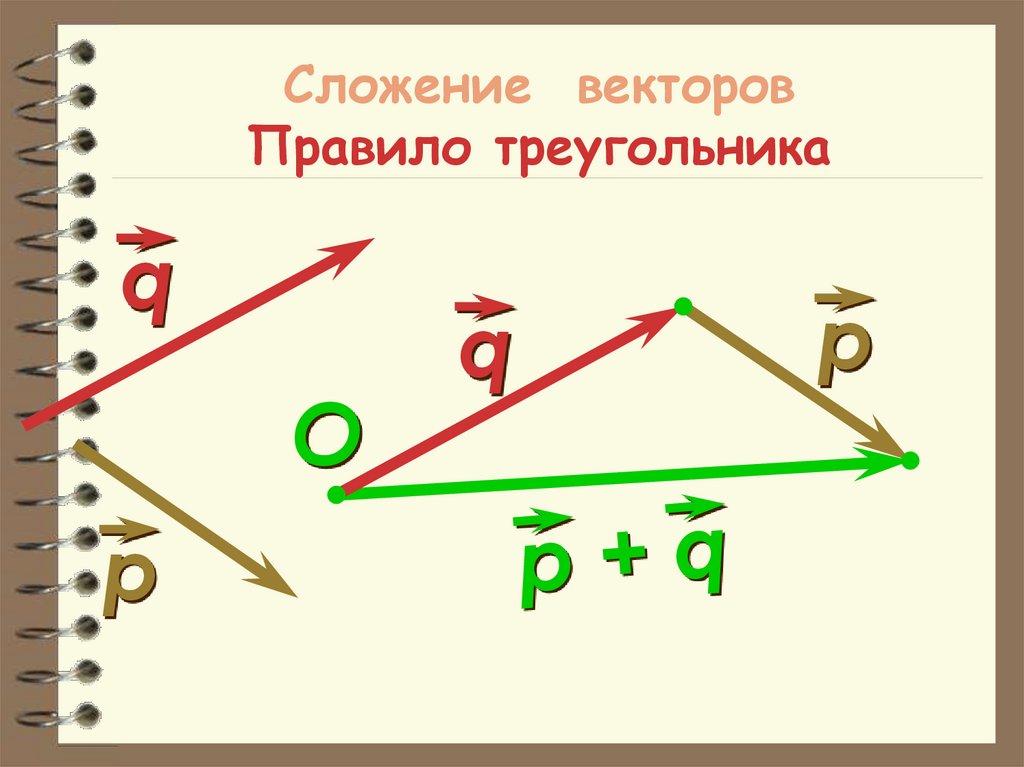
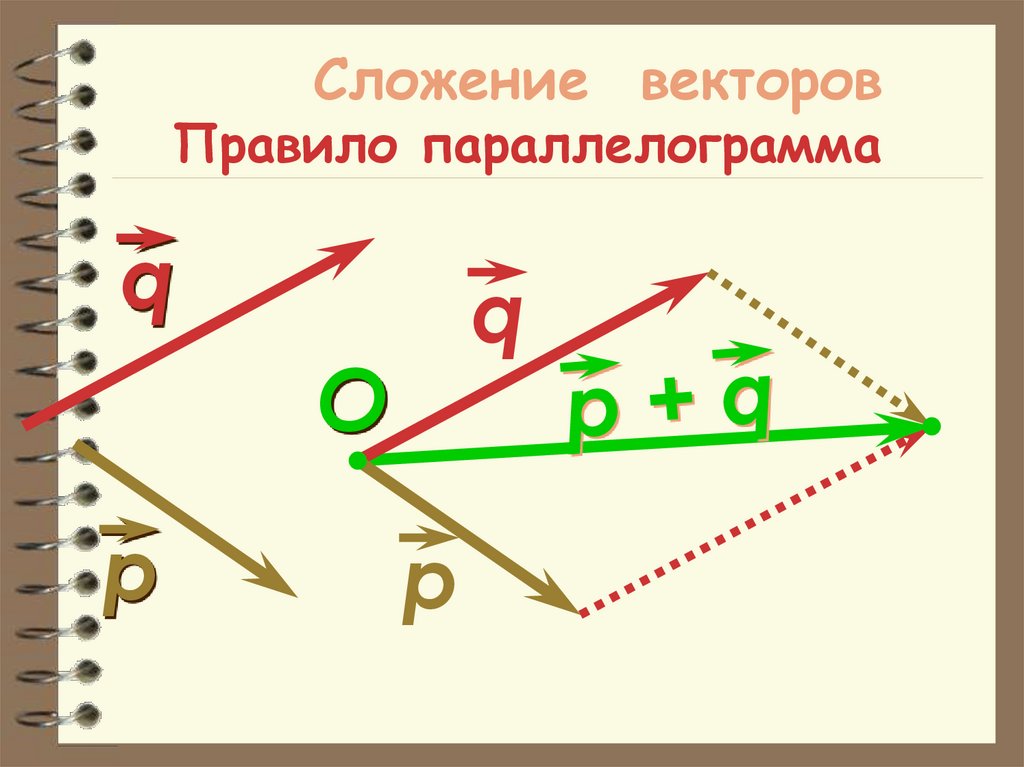
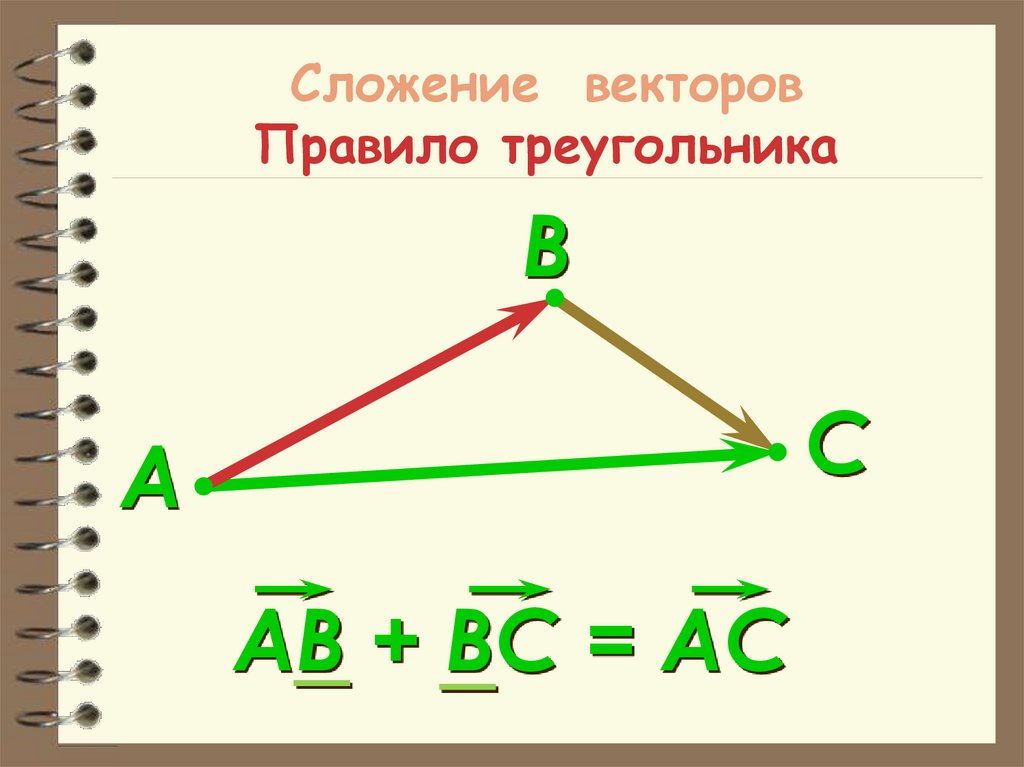
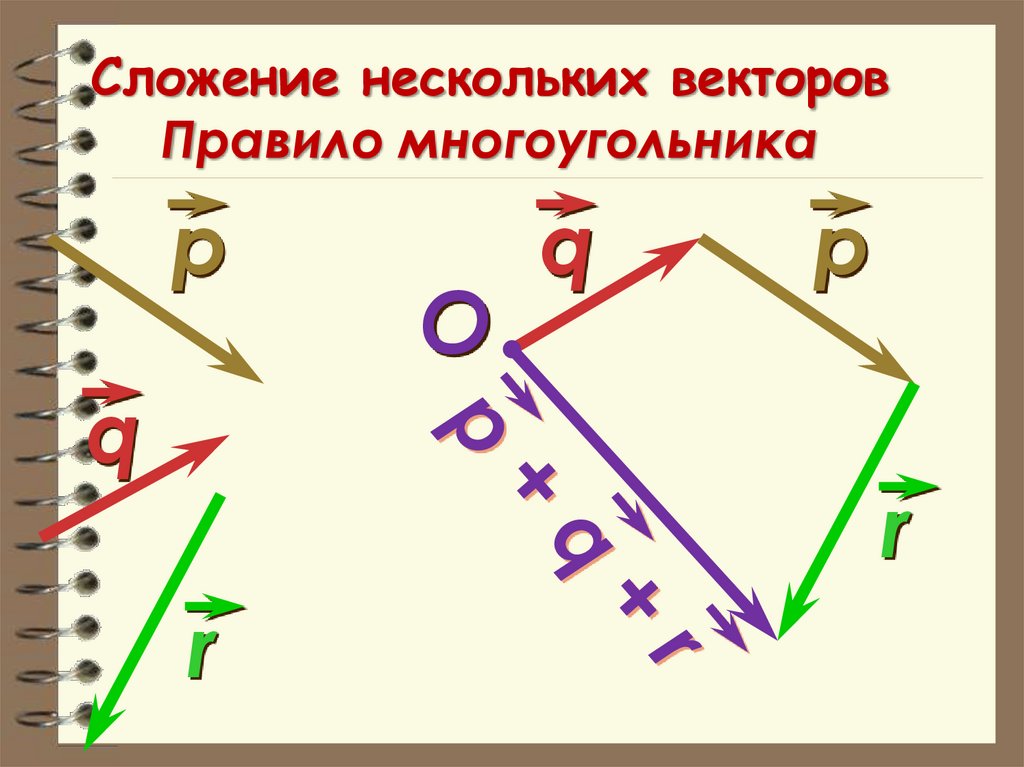
Сложение векторов
– Правило треугольника
– Правило параллелограмма
– Сложение нескольких векторов
Вычитание векторов
Произведение вектора на число

3. Историческая справка

Термин вектор (от лат. Vector
– « несущий» ) впервые
появился в 1845 г. у
ирландского математика
Уильяма Гамильтона (1805 –
1865) в работах по построению
числовых систем.

4.

Понятие вектора
Многие физические величины
характеризуются числовым значением и
направлением в пространстве, их называют
векторными величинами
v
F

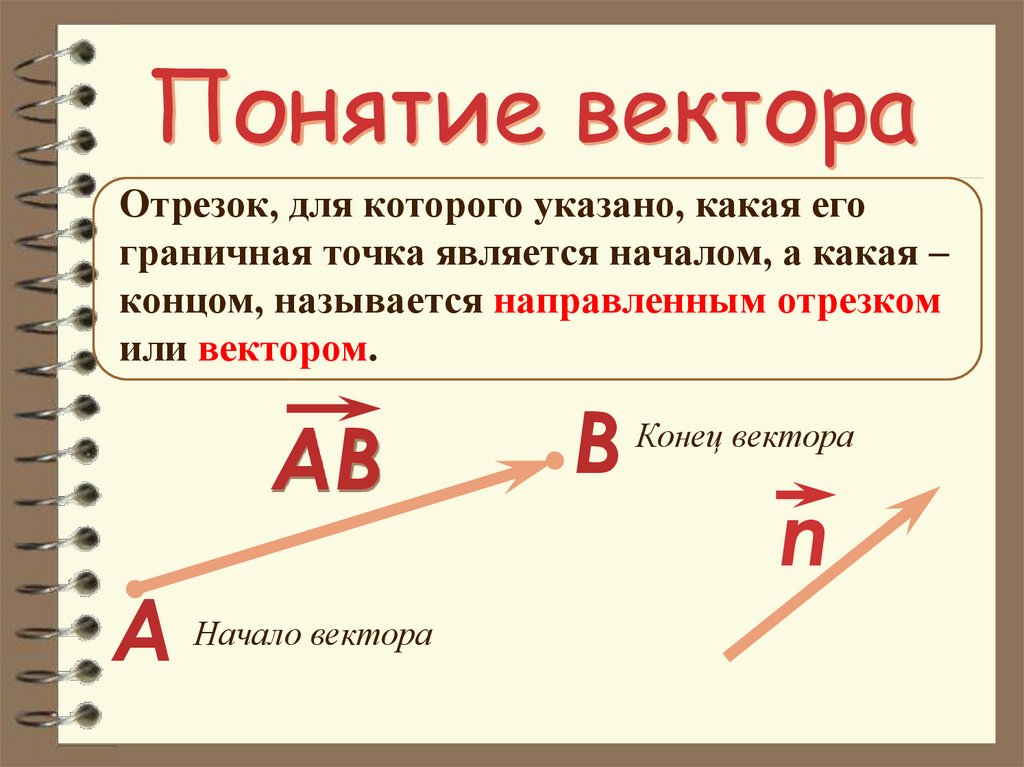
5. Понятие вектора

Отрезок, для которого указано, какая его
граничная точка является началом, а какая –
концом, называется направленным отрезком
или вектором.
АВ
А
Начало вектора
В
Конец вектора
n

6.

Вектор называется свободным, если его
значение не меняется при произвольном
параллельном переносе.
Свободным вектором является, например,
скорость движения материальной точки.
Вектор называется скользящим, если его
значение
не
меняется
при
любом
параллельном переносе вдоль линии его
действия.

7.

Примером скользящего вектора может
служить сила, действующая на абсолютно
твёрдое тело (две равные и расположенные
на одной прямой силы оказывают на
абсолютно
твёрдое
тело
одинаковое
воздействие).
Вектор
называется
связанным,
фиксировано его начало.
если

8.

Например, сила, приложенная к некоторой
точке упругого тела, представляет собой
связанный вектор.
Свойства свободных векторов изучаются
средствами векторной алгебры (Векторное
исчисление).
Общее понятие вектора, как элемента, так
называемого,
векторного
пространства
определяется аксиоматически.

9.

Векторное исчисление - математическая
дисциплина, в которой изучают свойства
операций
над
векторами
евклидова
пространства.
При этом понятие вектора представляет
собой
математическую
абстракцию
величин, характеризующихся не только
численным
значением,
но
и
направленностью
(например,
сила,
ускорение, скорость).

10.

Возникновение векторного исчисления тесно
связано с потребностями механики и физики.
До 19 в. для задания векторов использовался
лишь координатный способ, и операции над
векторами сводились к операциям над их
координатами.
Лишь в середине 19 в. усилиями ряда учёных
было создано векторное исчисление, в
котором
операции
проводились
непосредственно
над
векторами,
без
обращения к координатному способу задания.

11.

Основы
векторного
исчисления
были
заложены
исследованиями
английского
математика У. Гамильтона и немецкого
математика
Г.
Грассмана
по
гиперкомплексным числам (1844 - 50). Их
идеи
были
использованы
английским
физиком Дж. К. Максвеллом в его работах по
электричеству и магнетизму.

12.

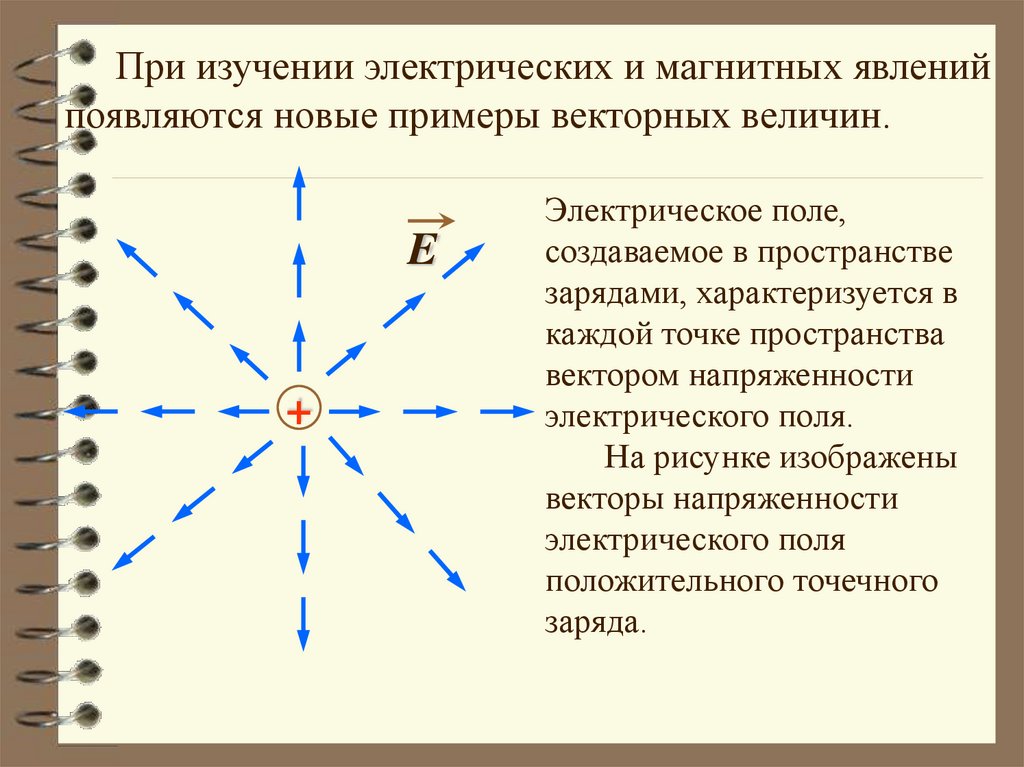
При изучении электрических и магнитных явлений
появляются новые примеры векторных величин.
E
+
Электрическое поле,
создаваемое в пространстве
зарядами, характеризуется в
каждой точке пространства
вектором напряженности
электрического поля.
На рисунке изображены
векторы напряженности
электрического поля
положительного точечного
заряда.

13.

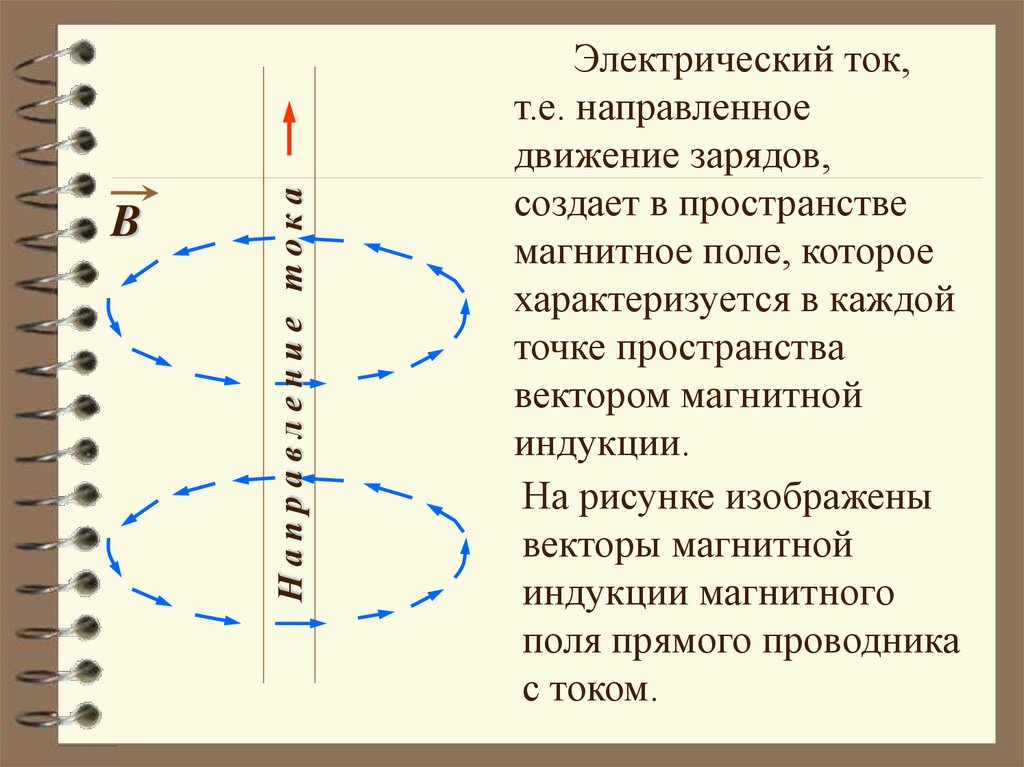
Направление тока
B
Электрический ток,
т.е. направленное
движение зарядов,
создает в пространстве
магнитное поле, которое
характеризуется в каждой
точке пространства
вектором магнитной
индукции.
На рисунке изображены
векторы магнитной
индукции магнитного
поля прямого проводника
с током.

14.

Современный вид векторному исчислению
придал американский физик Дж. Гиббс.
Значительный вклад в развитие векторного
исчисления внесли русские учёные.
В первую очередь следует отметить работы
М. В. Остроградского. Им была доказана
основная
теорема
векторного
анализа
(Остроградского формула).

15.

Исследования казанского математика А. П.
Котельникова по развитию винтового
исчисления имели важное значение для
механики и геометрии.
Эти
исследования
были
продолжены
советскими математиками Д. Н. Зейлигером и
А. Широковым. Большое влияние на развитие
В. и. имела книга «Векторный анализ»,
написанная в 1907 русским математиком П.
О. Сомовым.

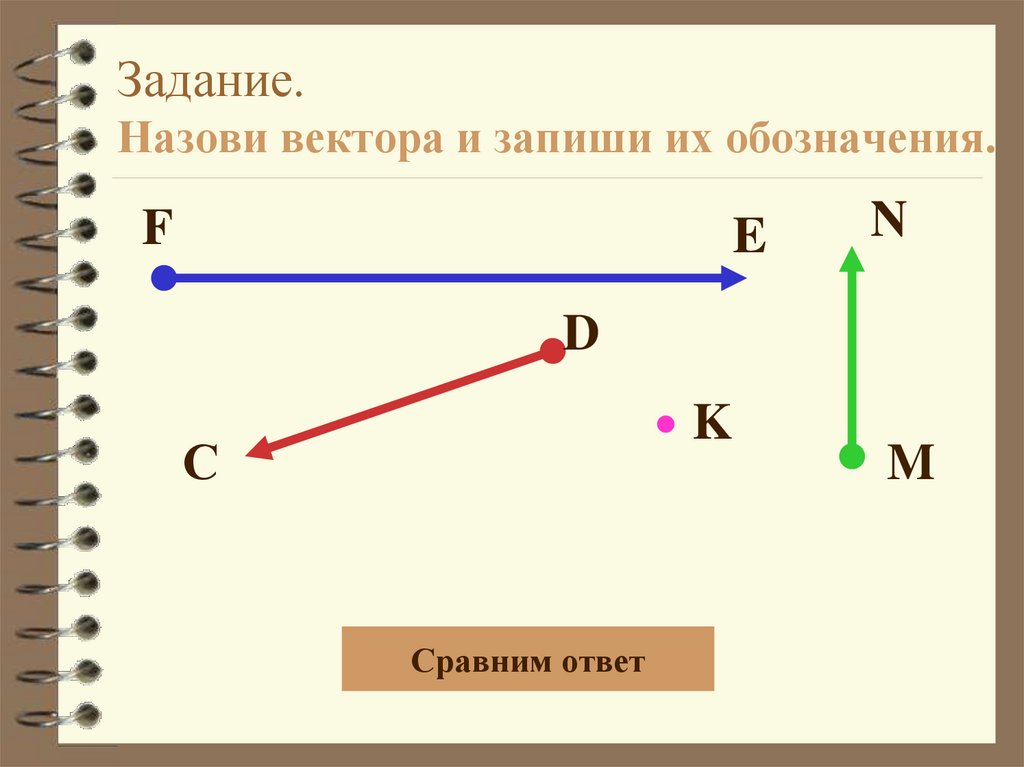
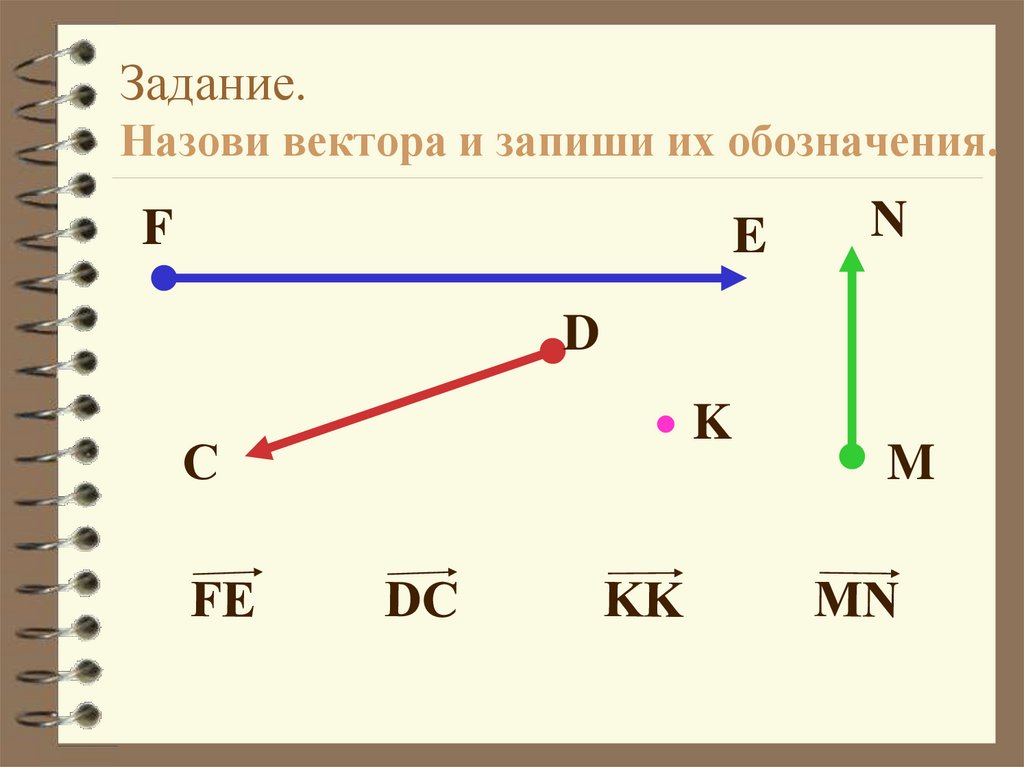
16. Задание. Назови вектора и запиши их обозначения.

F
E
N
D
K
С
Сравним ответ
M

17. Задание. Назови вектора и запиши их обозначения.

F
E
N
D
С
K
M

18. Длина вектора

N
Длиной вектора или модулем ненулевого
вектора называется длина отрезка.
|MN| = |a| длина вектора MN
a
M
Вектор, длина которого равна нулю
называется нулевой.
Вектор, длина которого равна единицы
называется единичным или орт - вектором.
K вектор КК или нулевой вектор, |KK| = 0

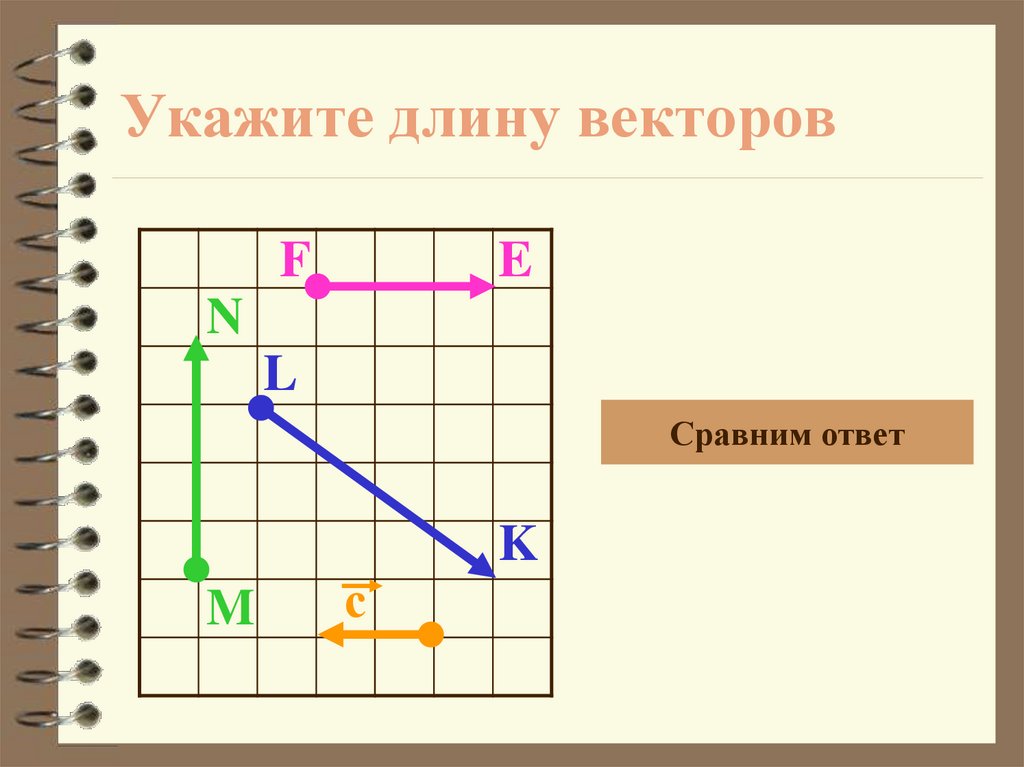
19. Укажите длину векторов

F
E
N
L
Сравним ответ
M
с
K

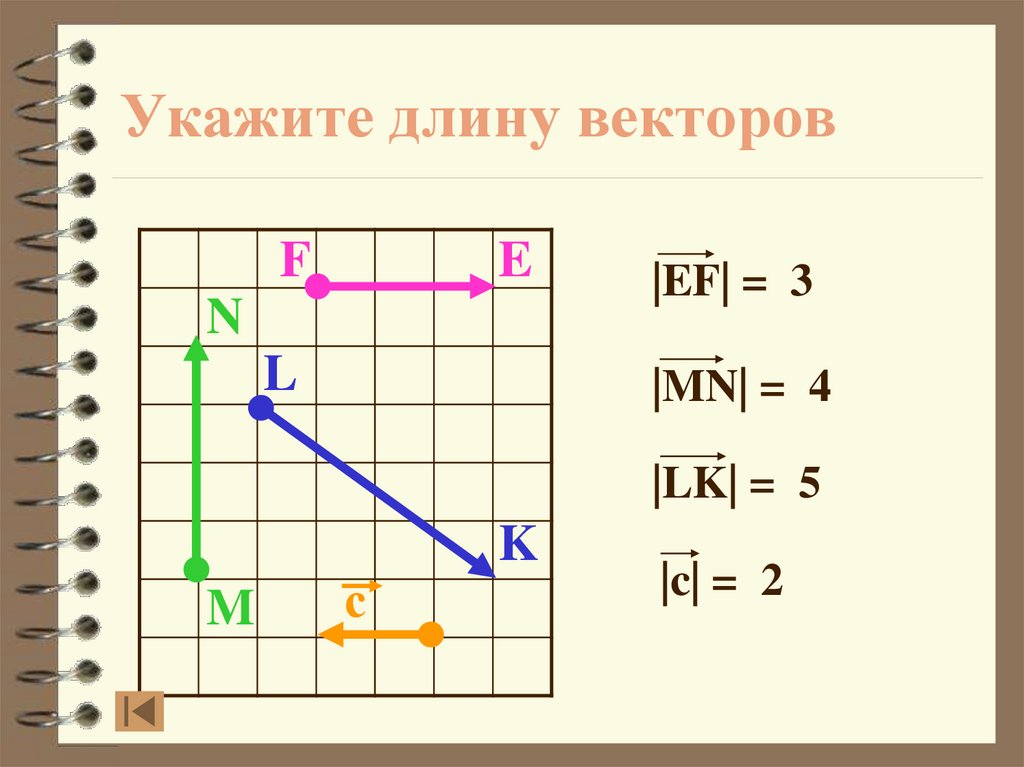
20. Укажите длину векторов

F
E
N
L
|EF| = 3
|MN| = 4
|LK| = 5
M
с
K
|c| = 2

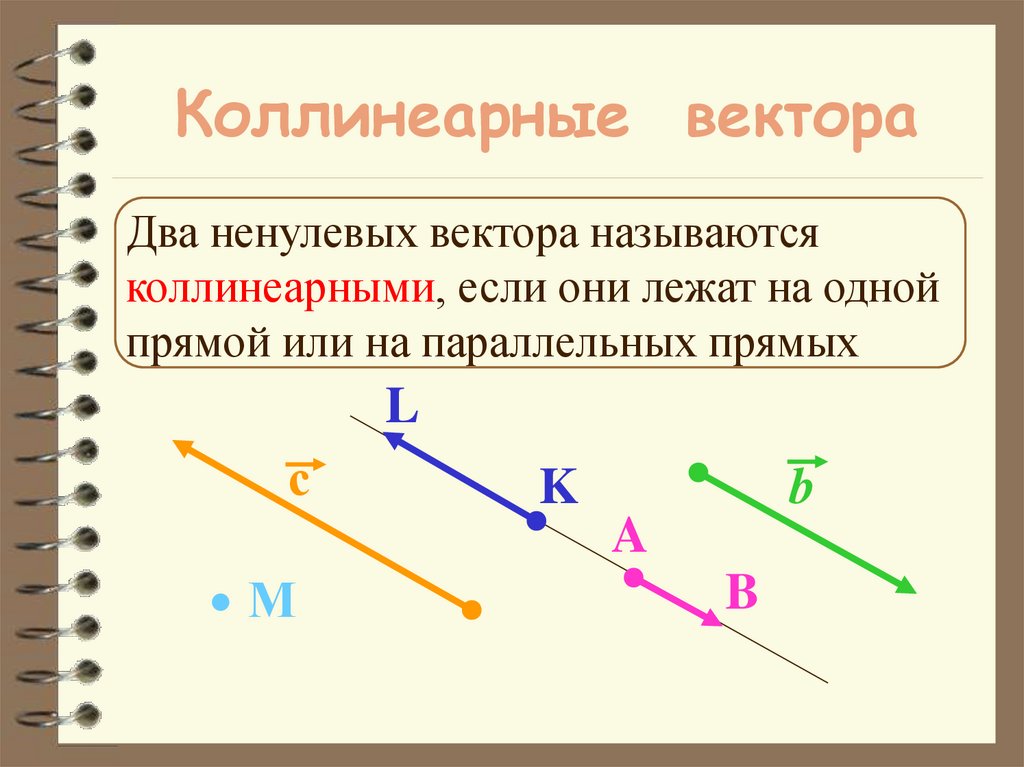
21. Коллинеарные вектора

Два ненулевых вектора называются
коллинеарными, если они лежат на одной
прямой или на параллельных прямых
L
с
K
b
A
М
B

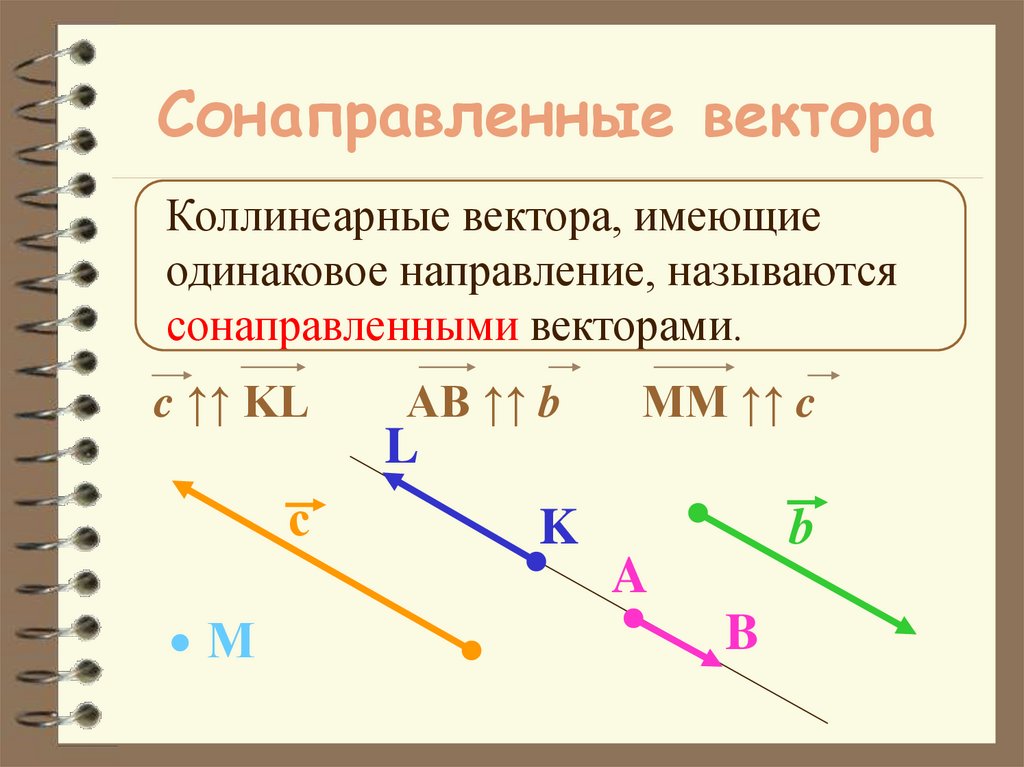
22. Сонаправленные вектора

Коллинеарные вектора, имеющие
одинаковое направление, называются
сонаправленными векторами.
c ↑↑ KL
AB ↑↑ b
MM ↑↑ c
L
с
K
b
A
М
B

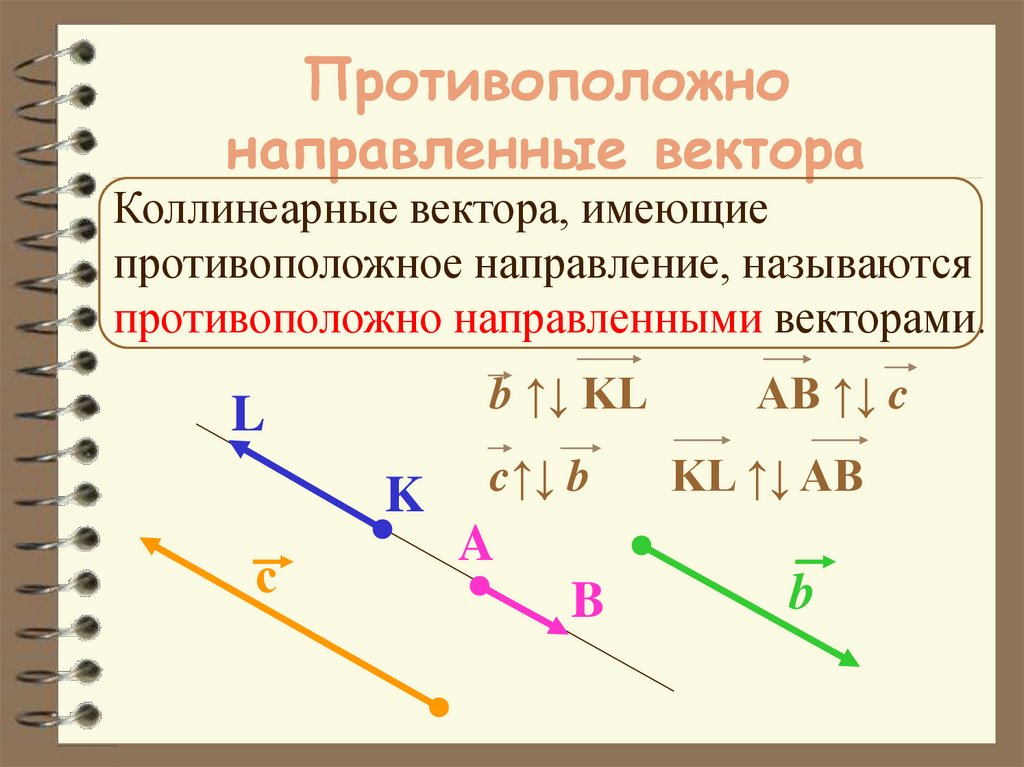
23. Противоположно направленные вектора

Коллинеарные вектора, имеющие
противоположное направление, называются
противоположно направленными векторами.
b ↑↓ KL
L
K
с
c↑↓ b
AB ↑↓ c
KL ↑↓ AB
A
B
b

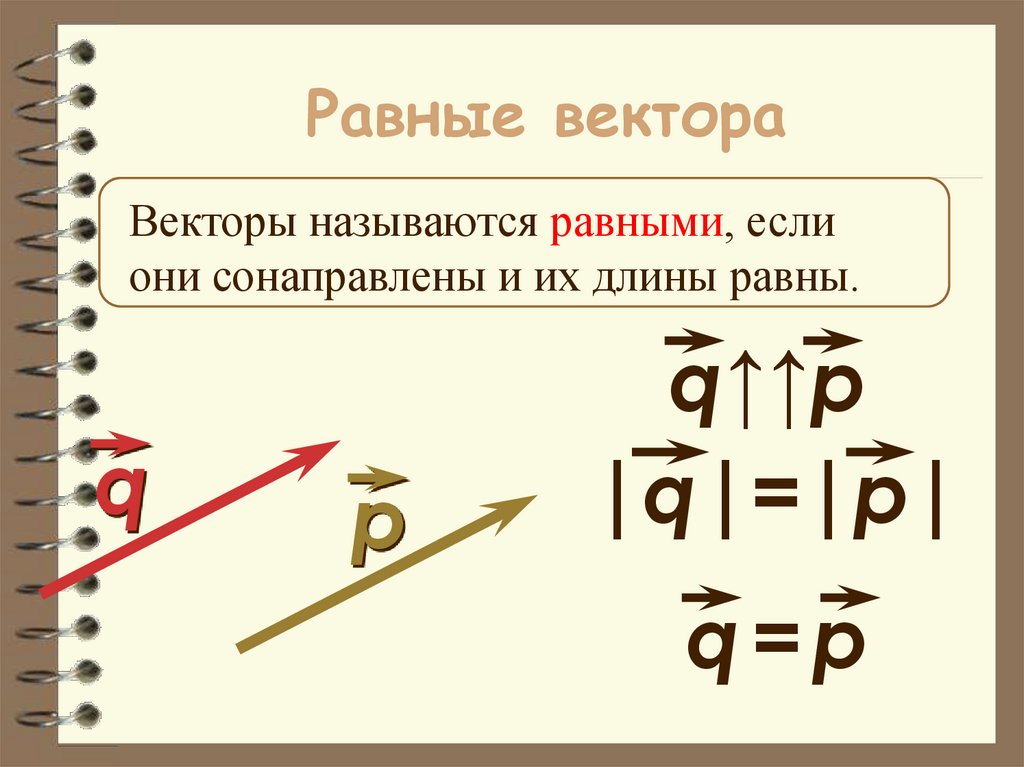
24. Равные вектора

Векторы называются равными, если
они сонаправлены и их длины равны.
q
р
q↑↑р
|q|=|р|
q=р

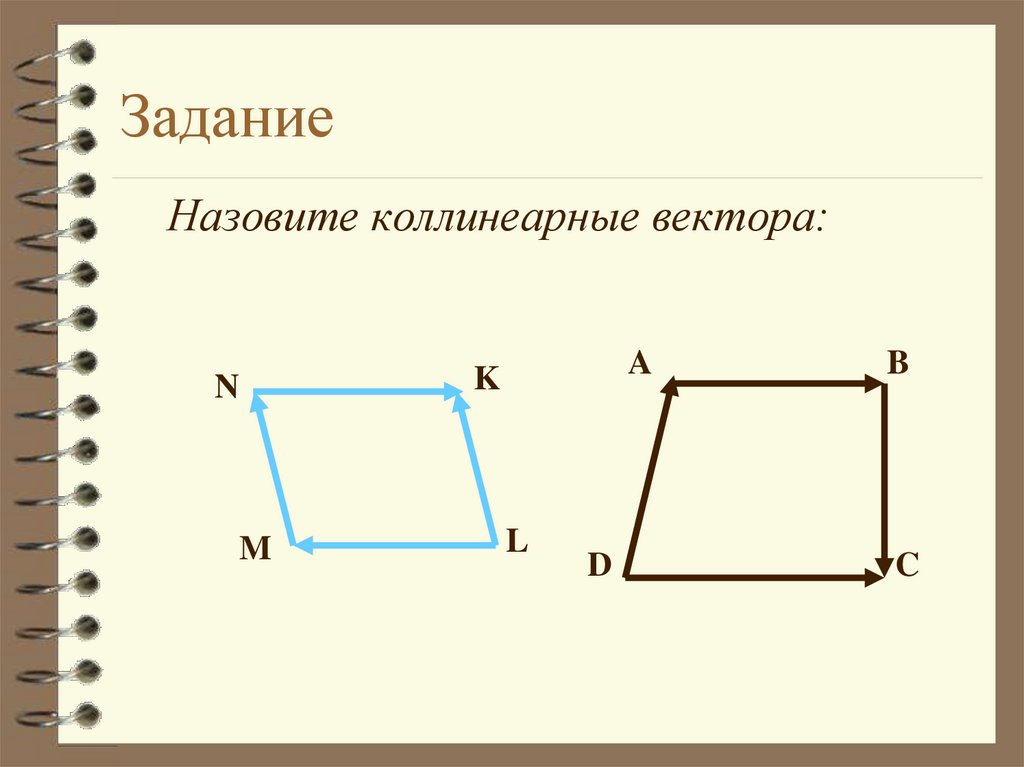
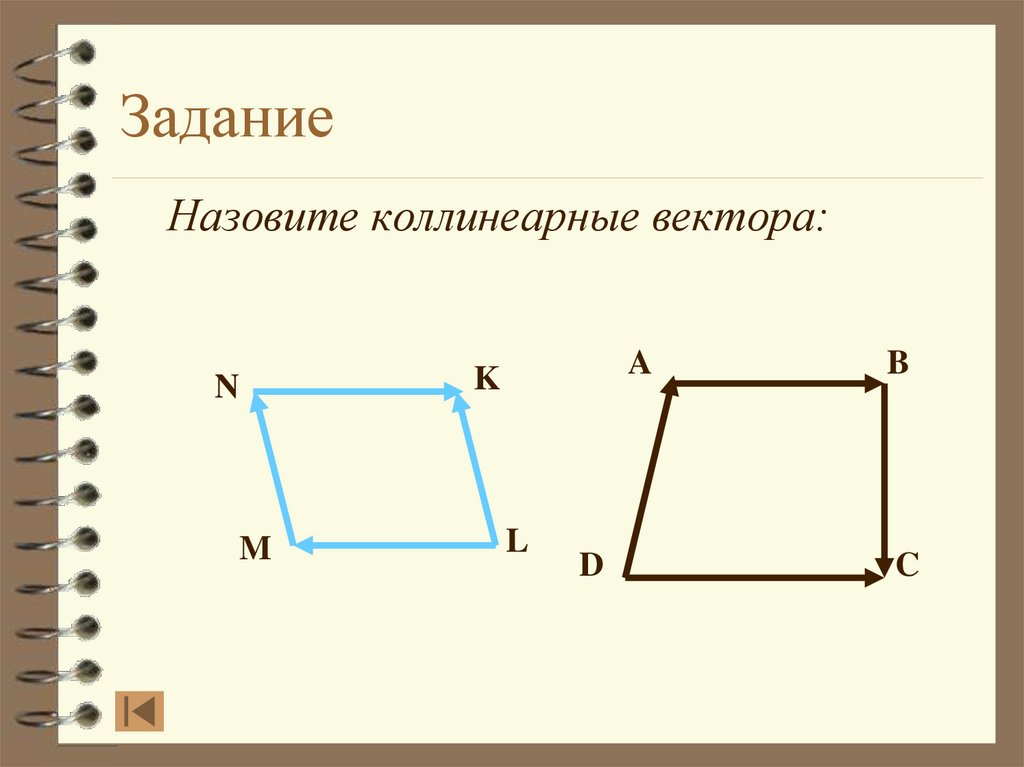
25. Задание

Назовите коллинеарные вектора:
N
M
A
K
L
D
B
C

26. Задание

Назовите коллинеарные вектора:
N
M
A
K
L
D
B
C

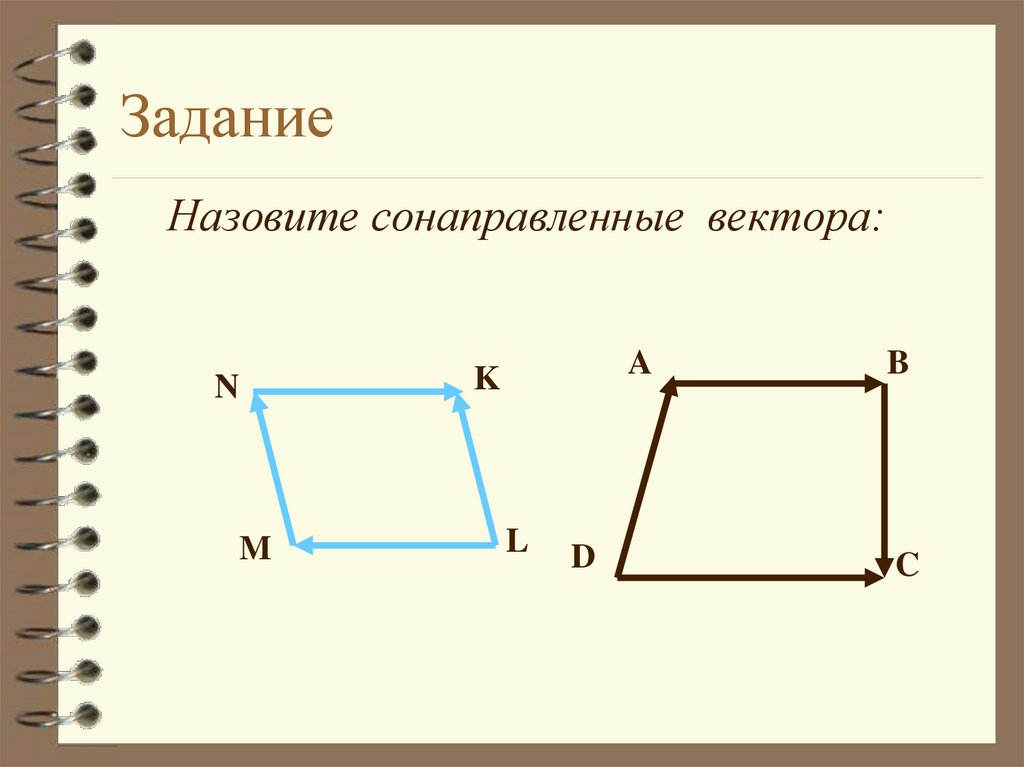
27. Задание

Назовите сонаправленные вектора:
N
M
A
K
L
D
B
C

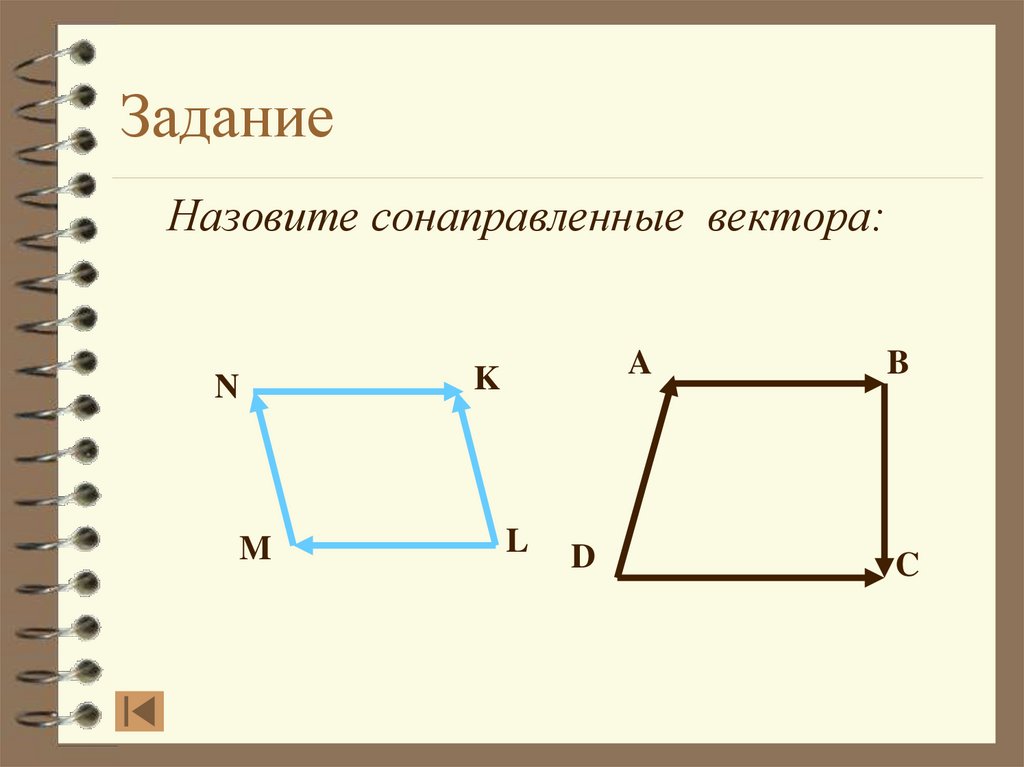
28. Задание

Назовите сонаправленные вектора:
N
M
A
K
L
D
B
C

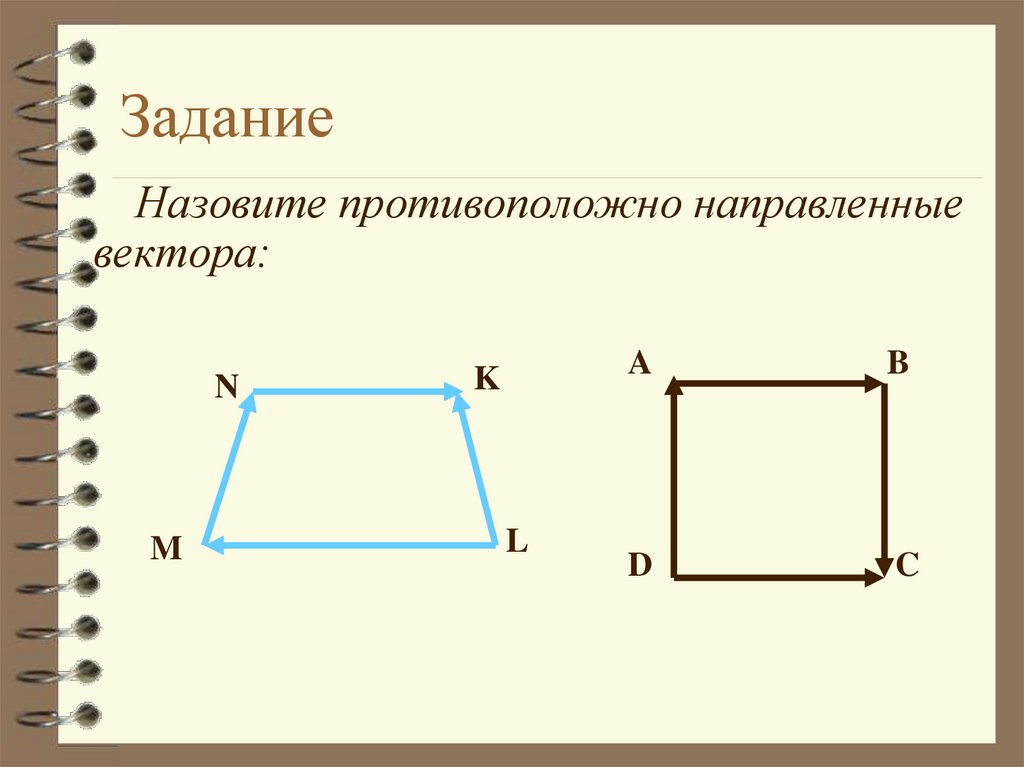
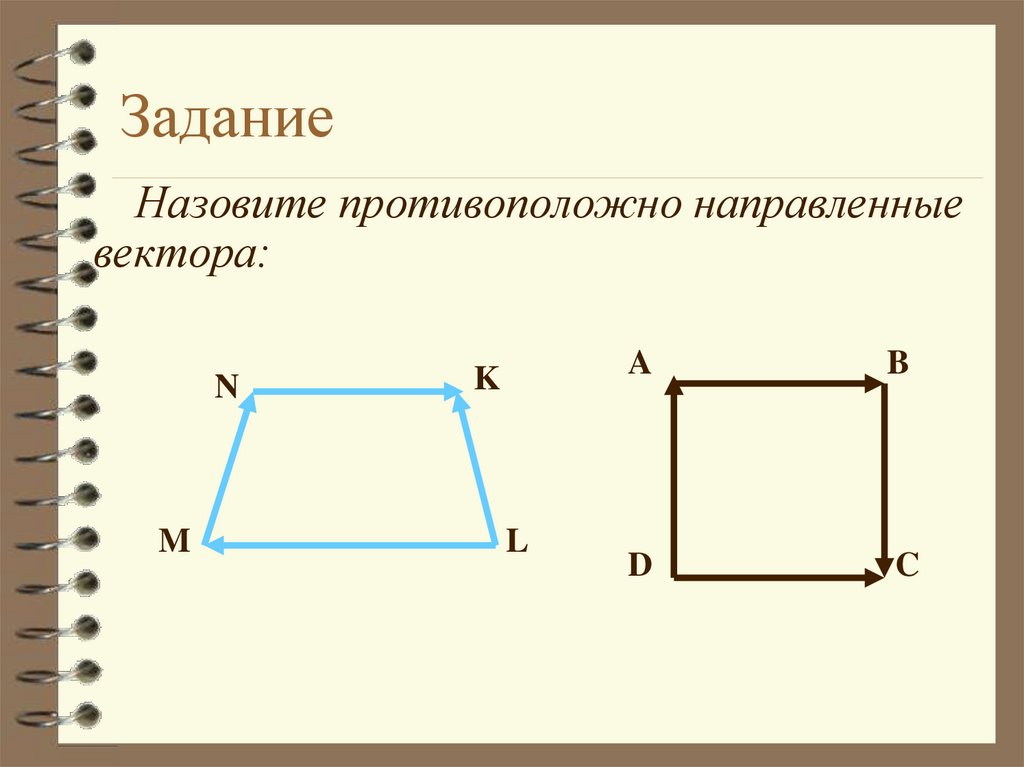
29. Задание

Назовите противоположно направленные
вектора:
N
M
K
L
A
B
D
C

30. Задание

Назовите противоположно направленные
вектора:
N
M
K
L
A
B
D
C

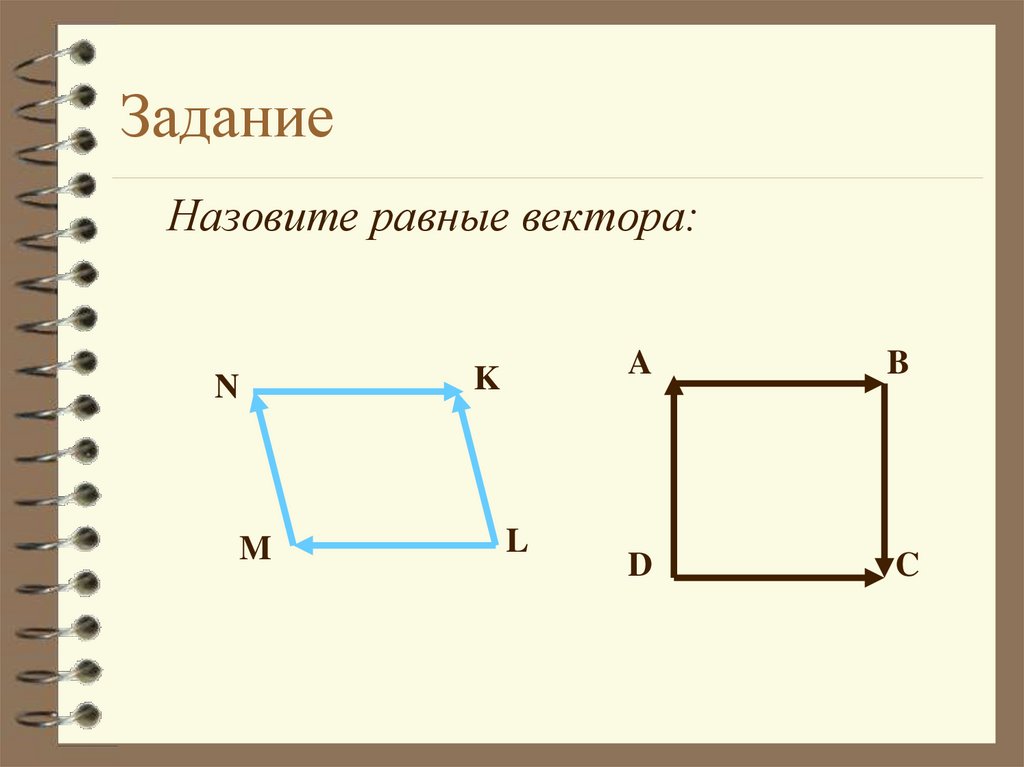
31. Задание

Назовите равные вектора:
N
M
K
L
A
B
D
C

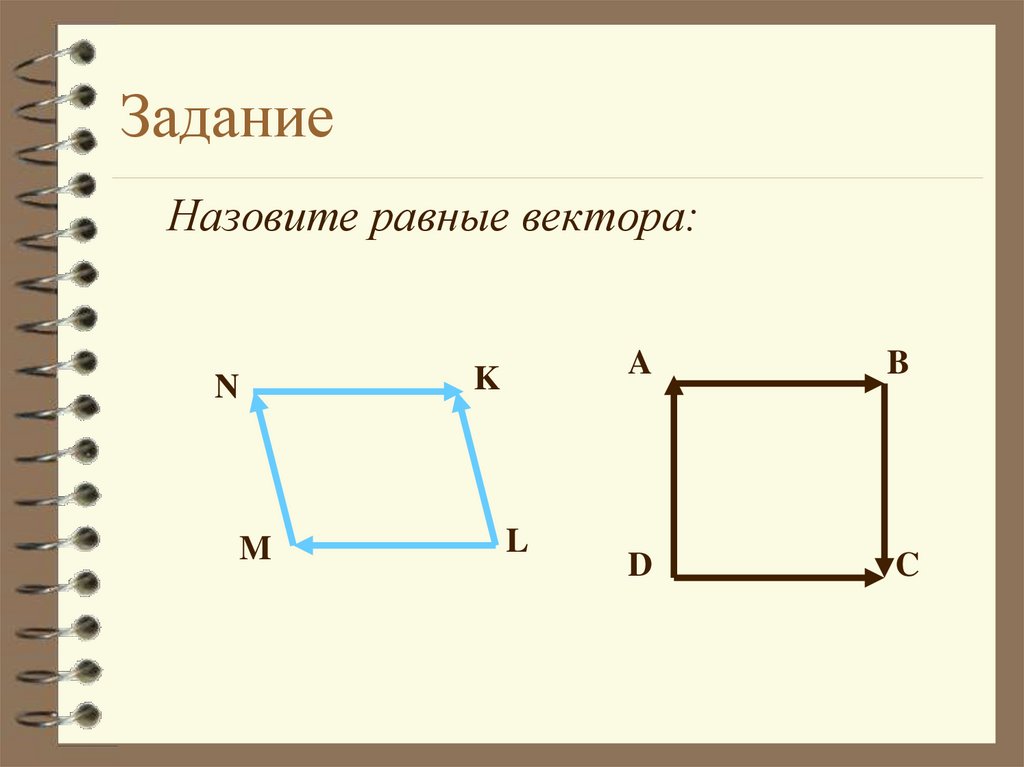
32. Задание

Назовите равные вектора:
N
M
K
L
A
B
D
C

33.

КОМПЛАНАРНЫЕ ВЕКТОРЫ
Три вектора называются компланарными, если
они лежат в одной плоскости или в параллельных
плоскостях.
D
Компланарные векторы
C
ED, OD и OE.
Некомпланарные векторы
E
B
О
A
OA, OB и OC.

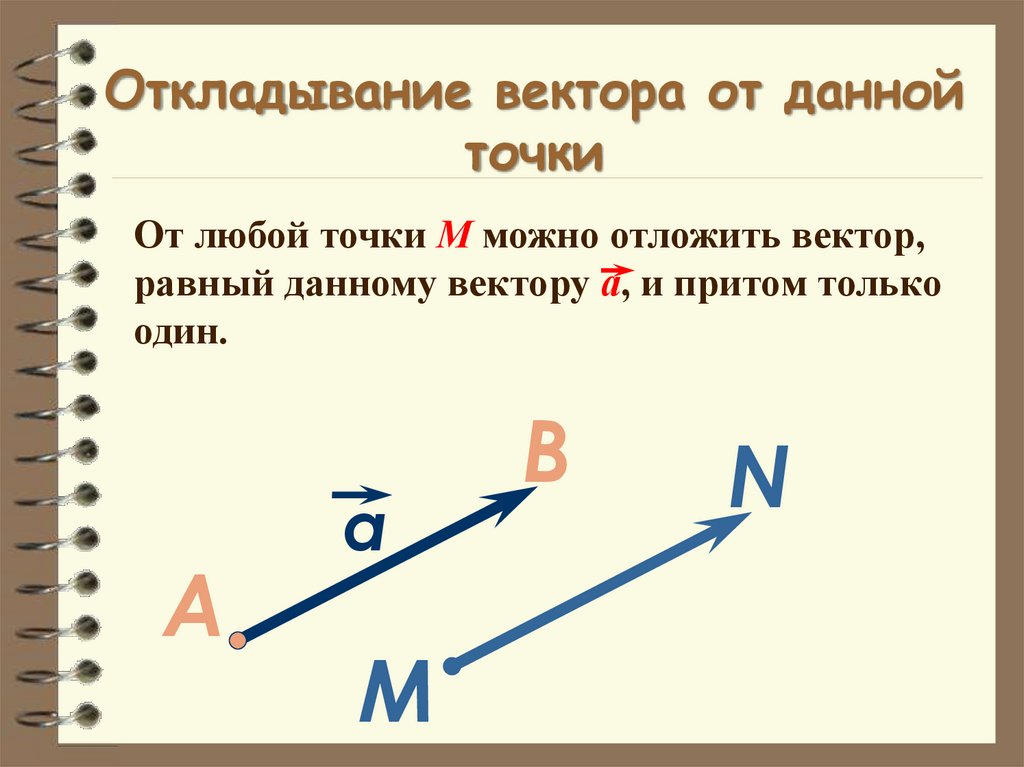
34. Откладывание вектора от данной точки

От любой точки М можно отложить вектор,
равный данному вектору а, и притом только
один.
А
a
М
В
N

35. Сложение векторов Правило треугольника

q
O
р
q
р

36. Сложение векторов Правило параллелограмма

q
q
O
р
р

37. Сложение векторов Правило треугольника

В
С
А
АВ + ВС = АС

38. Сложение нескольких векторов Правило многоугольника

р
q
O
q
р
r
r

39. Свойства сложения

а+b
=
b+a
− переместительный закон
(а + b) + с = (b + с) + a
− сочетательный закон
а−b
=
a +(− b)
− разность векторов

40. Вычитание векторов

Разностью двух векторов а и b называется такой
сумма которого с вектором b равна вектору а.
вектор,
Для любых векторов а и b справедливо равенство
а - b = а + (-b).
Задача. Даны векторы а и b. Построить вектор а – b.
b
-b
-b
а
а
a-b

41. Умножение вектора a на число k

k·a = b,
|a| ≠ 0, k – произвольное число
|b| = |k|·|a|,
если k>0, то a ↑↑ b
a
если k<0, то a ↑↓ b
2a
-2a
Для любых чисел k, l и любых векторов a, b справедливы равенства:
1º. (kl)a= k(la) (сочетательный закон),
2º. (k+l)a= ka+la (первый распределительный закон),
3º. k(a+b) = ka+kb (второй распределительный закон).

42.

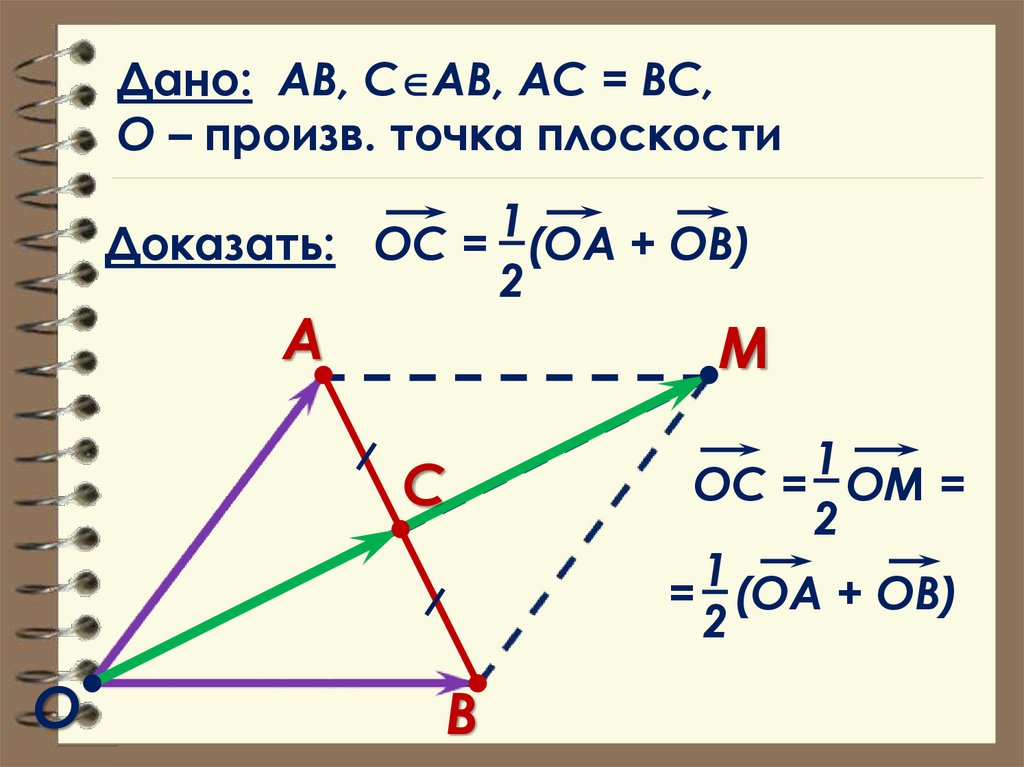
Дано: АВ, С АВ, АС = ВС,
О – произв. точка плоскости
1
Доказать: ОС = (ОА + ОВ)
2
А
М
С
О
В
1
ОС = ОМ =
2
1
= (ОА + ОВ)
2