Похожие презентации:
Глава IV. Векторы в пространстве
1.
Глава IV.Векторыв пространстве
2.
Понятие вектораМногие физические величины
характеризуются числовым значением и
направлением в пространстве, их
называют векторными величинами
v
F
3.
Понятие вектораОтрезок, для которого указано, какая
его граничная точка является началом,
а какая - концом, называется
направленным отрезком или вектором
AB
- вектор
B
Конец вектора
A
Начало вектора
4.
Задание 1Назови вектора и запиши их обозначения.
F
E
N
D
С
P
M
5.
Задание 1Назови вектора и запиши их обозначения.
F
E
N
D
С
P
M
6.
Длина векторавектор MN или вектор а
N
a
M
Длиной вектора или модулем
ненулевого вектора
называется длина отрезка MN
|MN| = |a| длина вектора MN
K вектор КК или нулевой
вектор |KK| = 0
7.
Укажите длину векторовF
E
N
L
M
с
K
8.
Укажите длину векторовF
N
E
L
|EF| = 3
|MN| = 4
|c| = 2
M
с
K
|LK| = 5
№ 320(а),321(а)
9. Векторы
коллинеарныесонаправленные
неколлинеарные
противоположно
направленные
10.
Коллинеарные вектораНенулевые вектора называются
коллинеарными, если они лежат на
одной прямой или на параллельных
прямых L
с
K
b
A
B
Нулевой вектор считается
коллинеарным любому вектору
М
11.
Задание 2Назовите коллинеарные вектора:
Вариант 1
N
M
Вариант 2
A
K
L
D
B
C
12.
Сонаправленные вектораКоллинеарные вектора имеющие
одинаковое направление, называются
сонаправленными векторами
c ↑↑ KL
AB ↑↑ b
MM ↑↑ c (любому
вектору)
L
с
K
b
A
М
B
13.
Задание 2Назовите сонаправленные вектора:
Вариант 1
N
M
Вариант 2
A
K
L
D
B
C
14.
Противоположно направленныевектора
Коллинеарные вектора имеющие
противоположное направление,
называются противоположно
направленными векторами
L
b ↑↓ KL
AB ↑↓ c
K
с
A
c↑↓ b
B
KL ↑↓ AB
b
15.
Задание 3Назовите противоположно
направленные вектора:
Вариант 1
N
M
Вариант 2
K
L
A
B
D
C
16.
Равенство векторовВекторы называются равными, если они
сонаправлены и их длины равны
c ↑↑ KL, | c | = | LK | c = LK
L
с
K
b
A
B
17.
Задание 4Назовите равные вектора:
Вариант 1
N
M
Вариант 2
K
L
A
B
D
C
18. Векторы
коллинеарныесонаправленные
a
b
a b
неколлинеарные
противоположно
направленные
c
d
c d
e
f
19.
Равенство векторовВекторы называются равными, если они
сонаправлены и их длины равны
a ↑↑ b, | a| = | b | a = b
a
b
20.
№ 322M
K
21.
№ 326M
K
22. Действия над векторами.
1. Сложение векторов.2. Вычитание векторов.
3. Умножение вектора на число.
23.
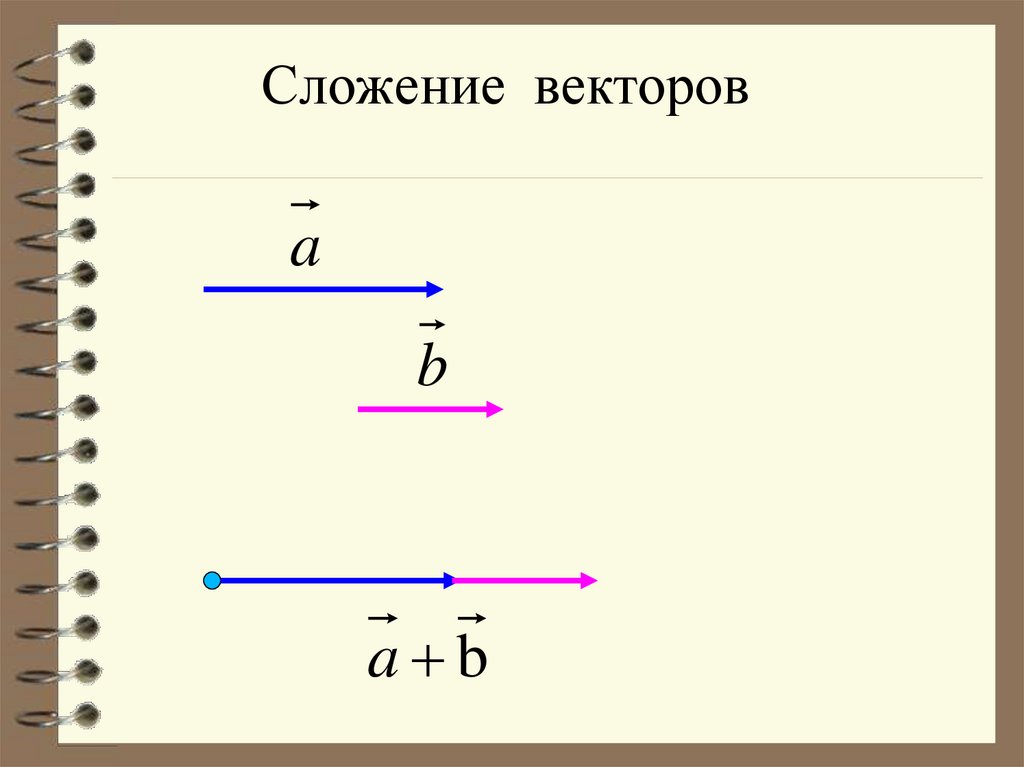
Сложение векторовПравило треугольника
b
Дано: a, b
a
Построить: c = a + b
Построение:
b
с
a
a+b=c
24.
Сложение векторовa
b
a b
25.
Сложение векторовa
b
a b
26.
Сложение векторовПравило треугольника для любых
трёх точек А, B,C:
AB BC AC
B
A
C
27.
Сложение векторовПравило параллелограмма
b
Дано: a, b
a
Построить: c = a + b
Построение:
с
b
a
a+b=c
28.
АВ
С
D
Постройте векторы:
RN NO RO
H
F
K
R
RN NK RK
B
B
C A
C
AB TU A
N
M
L
O
S
T
P
U
29.
АВ
С
D
Постройте векторы:
DA DU DR
H
F
K
N
M
R
S
L
O
T
P
U
RN RT RP
FM FH FN
30.
Сумма нескольких векторовa +b+ c+ d+ m+ n
b
a
b
n
a
m
c
m
n
d
c
d
31. Противоположные векторы
Два ненулевых вектора называютсяпротивоположными, если их длины равны
и они противоположно направлены.
Вектором, противоположным нулевому
вектору, считается нулевой вектор.
B
A
AB и BA противоположные
векторы.
32.
Вычитание векторовb
Дано: a, b
Построить: c = a - b
a
Построение:
-b
a
с
a-b=c
33.
аа
в
А
О
в
O
A O
B B
A
Как проверить?
O
B B
A O
A
В
34.
АВ
H
F
N
M
R
S
С
D
K
L
O
P
T
U
Постройте векторы:
BF BC CF
NM NU UM
LC LO OC
MH MS SH
35.
№ 329 - устно№ 335(а,б)
36.
Умножение вектора a на число kk·a = b,
|a| ≠ 0, k – произвольное число
|b| = |k|·|a|,
если k>0, то a ↑↑ b
если k<0, то a ↑↓ b
2a
a
-2a
37.
От точки N отложитевекторы
в
3в
2а
а
а
3в
а
N
в
2а
в
38.
Задача. Даны три вектора: a, b, cПостроить вектора:
p
2
a
2
b
2
c
1
q a b 3c
2





































 Физика
Физика








