Симметрия кристаллов

1.

СИММЕТРИЯ
КРИСТАЛЛОВ
Описание кристаллической структуры: узлы кристаллической решетки,
примитивная ячейка, векторы трансляций
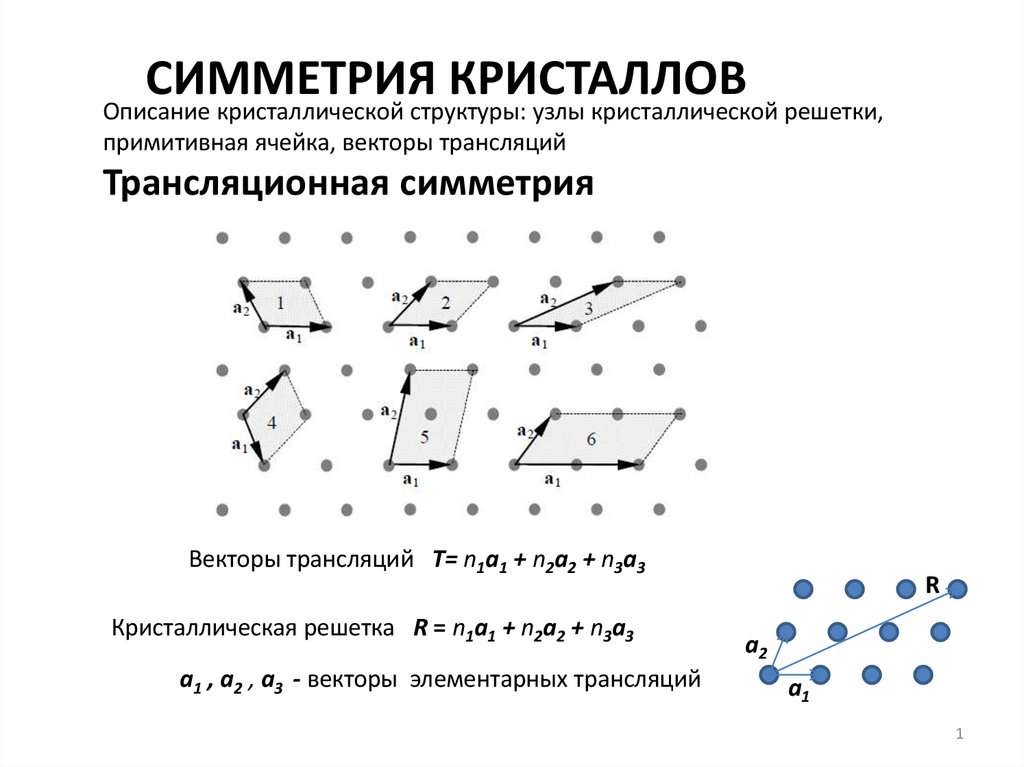
Трансляционная симметрия
Векторы трансляций T= n1a1 + n2a2 + n3a3
Кристаллическая решетка R = n1a1 + n2a2 + n3a3
a1 , a2 , a3 - векторы элементарных трансляций
R
a2
a1
1

2.

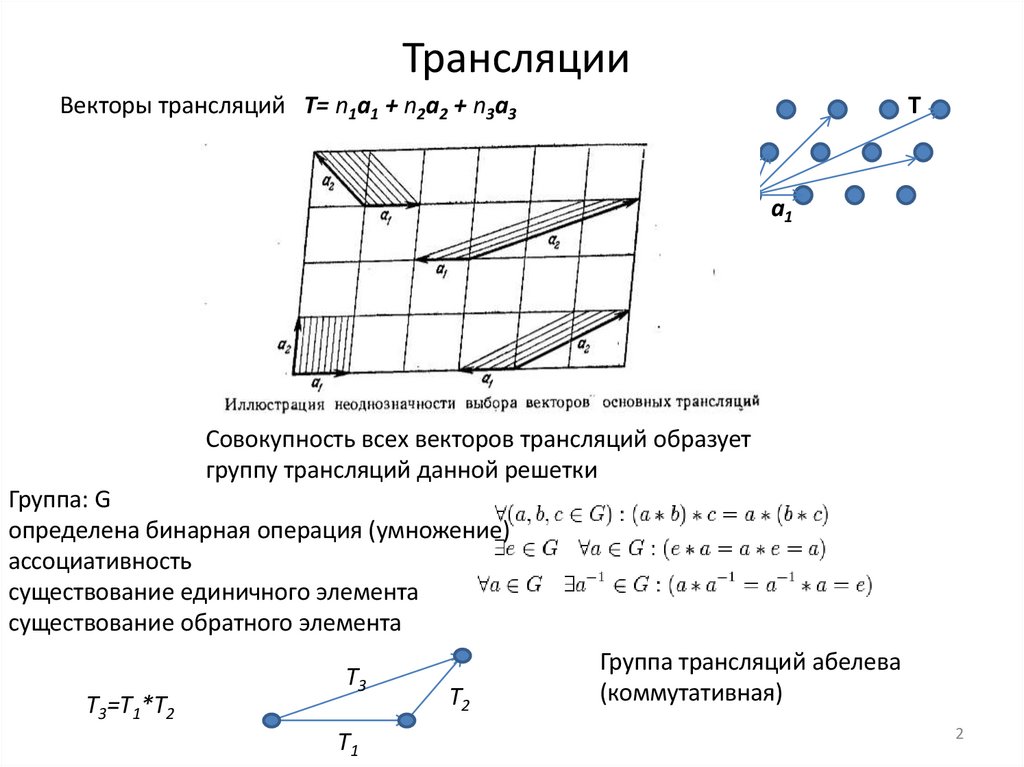
Трансляции
Векторы трансляций T= n1a1 + n2a2 + n3a3
T
a2
a1
Совокупность всех векторов трансляций образует
группу трансляций данной решетки
Группа: G
определена бинарная операция (умножение)
ассоциативность
существование единичного элемента
существование обратного элемента
Т3=Т1*Т2
Т3
Т1
Т2
Группа трансляций абелева
(коммутативная)
2

3.

Точечные группы симметрии
операции оставляют хотя бы одну точку пространства на месте:
вращение (элементы симметрии – оси вращения)
отражение (плоскости отражения)
инверсия (центр инверсии)
Пример – плоская квадратная решетка
ось вращения С4
плоскость отражения
4
1
2
3
3
2
1
4
центр инверсии
3

4.

Разрешенные вращения
A’B’=pa1=
p=-1,0,1,2,3
cos = 1, ½, 0, -1/2, -1
= 2 , 2 /6, /2, 2 /3,
4

5.

Классификация кристаллов: Сингонии
В зависимости от соотношения между длинами элементарных трансляций и
углами между ними выделяют шесть различных сингоний,
которые собраны в три группы в зависимости от числа равных длин
трансляций.
a1
a2
a3
•Низшая категория (все длины трансляций не равны друг другу)
a1 a2 a3
•Триклинная:
90
•Моноклинная: a1 a2 a3
90 , 90
•Ромбическая: a1 a2 a3
90
•Средняя категория (две длины трансляций из трёх равны между собой)
•Тетрагональная: a1 a2 a3
90
•Гексагональная: a1 a2 a3
90 , 120
•Высшая категория (все длины трансляций равны между собой)
•Кубическая: a1 a2 a3
90
5

6.

Классификация кристаллов: кристаллические системы
7 кристаллических систем – классификация по набору элементов точечной
симметрии, описывающих кристалл (по макроскопическим свойствам кристалла и
по внешнему виду). 7 точечных групп симметрии.
Низшая категория (нет осей высшего порядка)
•Триклинная: нет симметрии или только центр инверсии
•Моноклинная: одна ось 2-го порядка и/или плоскость симметрии m
•Ромбическая: три взаимно-перпендикулярных оси 2-го порядка и/или
плоскости симметрии m
Средняя категория (одна ось высшего порядка)
•Тетрагональная: одна ось 4-го порядка
•Тригональная (ромбоэдрическая): одна ось 3-го порядка
•Гексагональная: одна ось 6-го порядка
Высшая категория (несколько осей высшего порядка)
•Кубическая: четыре оси 3-го порядка
6

7.

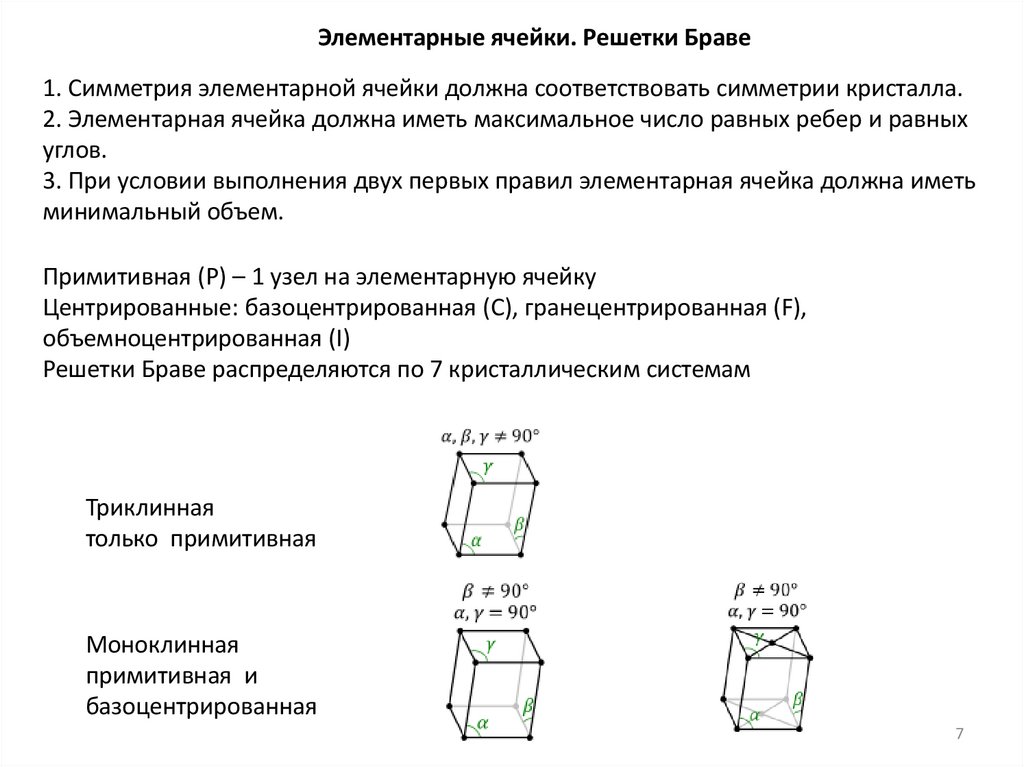
Элементарные ячейки. Решетки Браве
1. Симметрия элементарной ячейки должна соответствовать симметрии кристалла.
2. Элементарная ячейка должна иметь максимальное число равных ребер и равных
углов.
3. При условии выполнения двух первых правил элементарная ячейка должна иметь
минимальный объем.
Примитивная (P) – 1 узел на элементарную ячейку
Центрированные: базоцентрированная (C), гранецентрированная (F),
объемноцентрированная (I)
Решетки Браве распределяются по 7 кристаллическим системам
Триклинная
только примитивная
Моноклинная
примитивная и
базоцентрированная
7

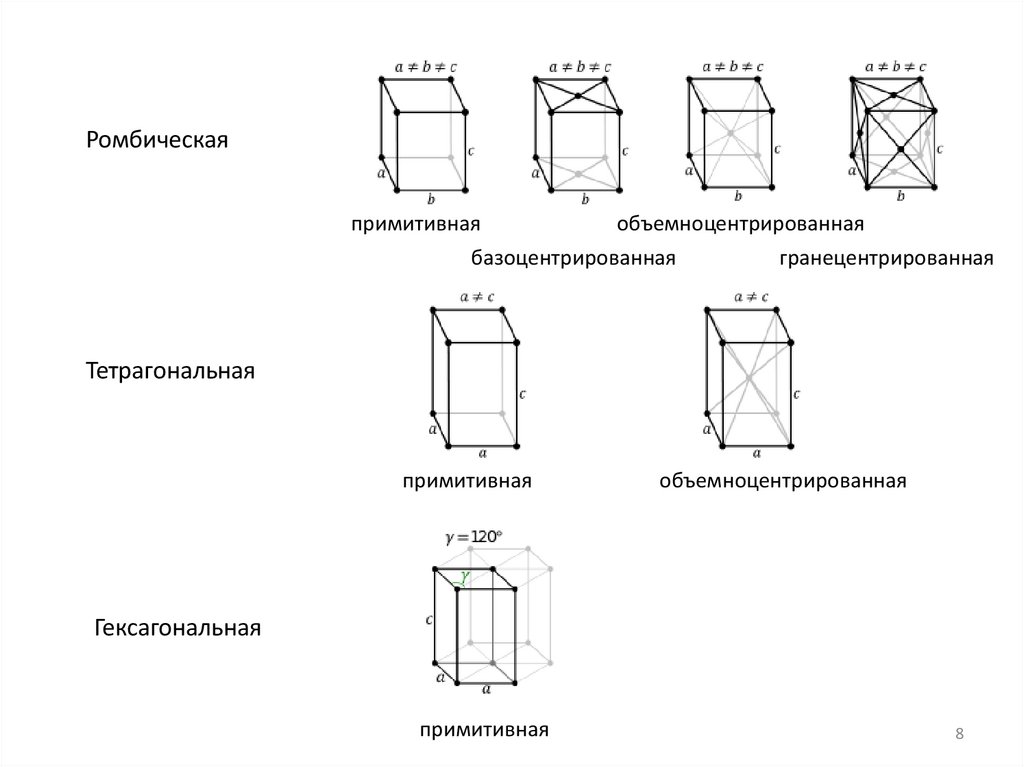
8.

Ромбическая
примитивная
объемноцентрированная
базоцентрированная
гранецентрированная
Тетрагональная
примитивная
объемноцентрированная
Гексагональная
примитивная
8

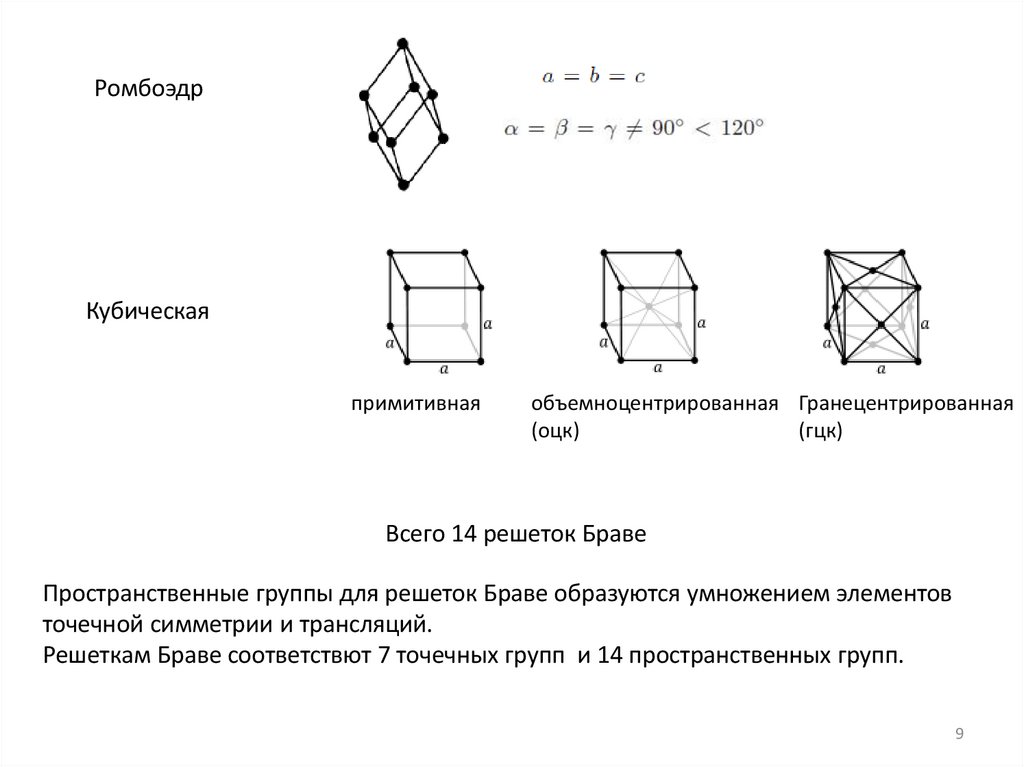
9.

Ромбоэдр
Кубическая
примитивная
объемноцентрированная Гранецентрированная
(оцк)
(гцк)
Всего 14 решеток Браве
Пространственные группы для решеток Браве образуются умножением элементов
точечной симметрии и трансляций.
Решеткам Браве соответствют 7 точечных групп и 14 пространственных групп.
9

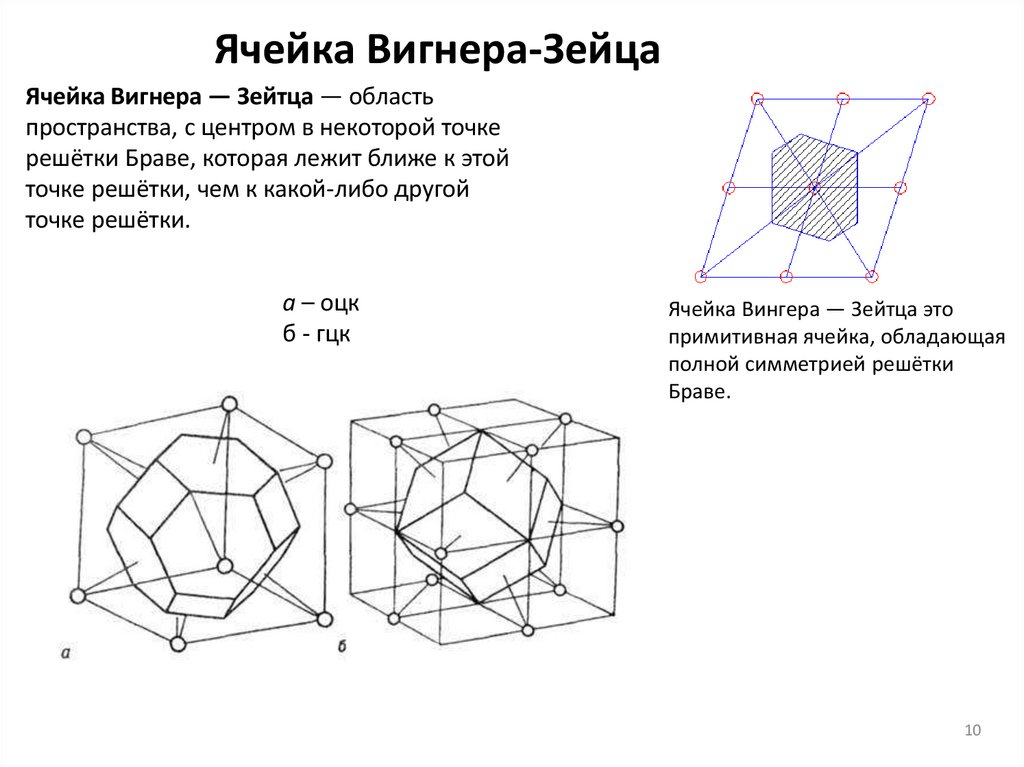
10.

Ячейка Вигнера-Зейца
Ячейка Вигнера — Зейтца — область
пространства, с центром в некоторой точке
решётки Браве, которая лежит ближе к этой
точке решётки, чем к какой-либо другой
точке решётки.
а – оцк
б - гцк
Ячейка Вингера — Зейтца это
примитивная ячейка, обладающая
полной симметрией решётки
Браве.
10

11.

Решетки с базисом
Добавляются винтовые оси (повороты вокруг оси с одновременным переносом на некоторый
вектор в направлении этой оси) и плоскости скользящего отражения (отражение
относительно плоскости с одновременным сдвигом на некоторый вектор, параллельный этой
плоскости).
Решеткам с базисом соответствует 32 группы точечной симметрии (32 класса
симметрии кристаллов) и 230 пространственных групп.
11

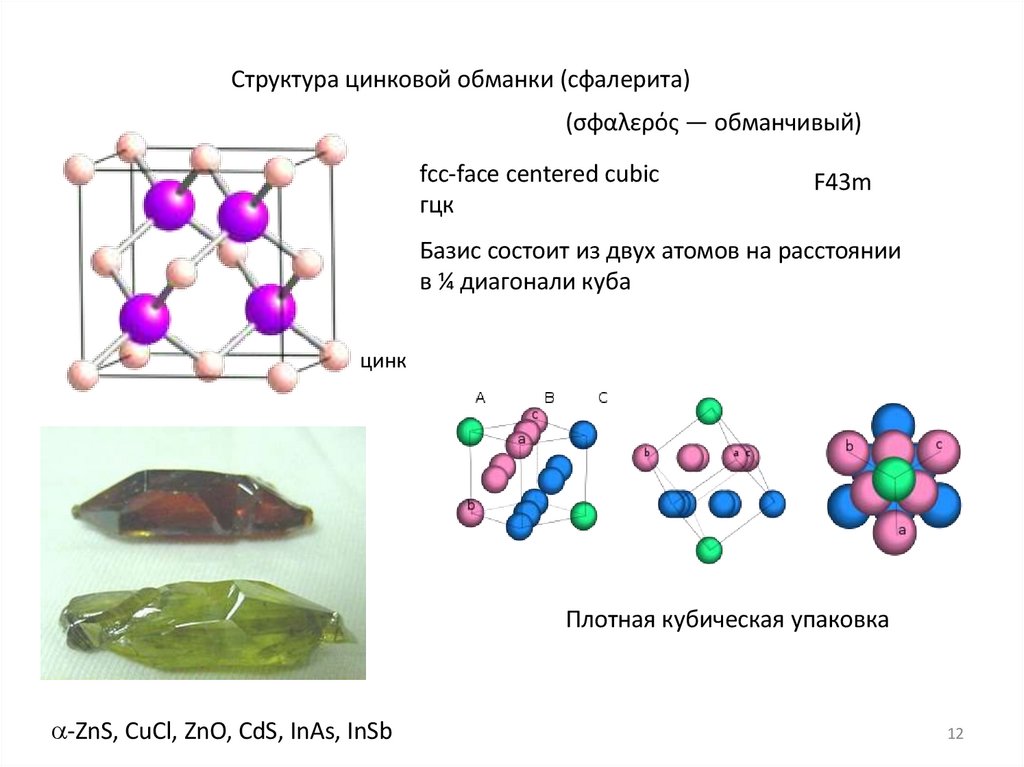
12.

Структура цинковой обманки (сфалерита)
(σφαλερός — обманчивый)
fcc-face centered cubic
гцк
F43m
Базис состоит из двух атомов на расстоянии
в ¼ диагонали куба
цинк
Плотная кубическая упаковка
-ZnS, CuCl, ZnO, CdS, InAs, InSb
12

13.

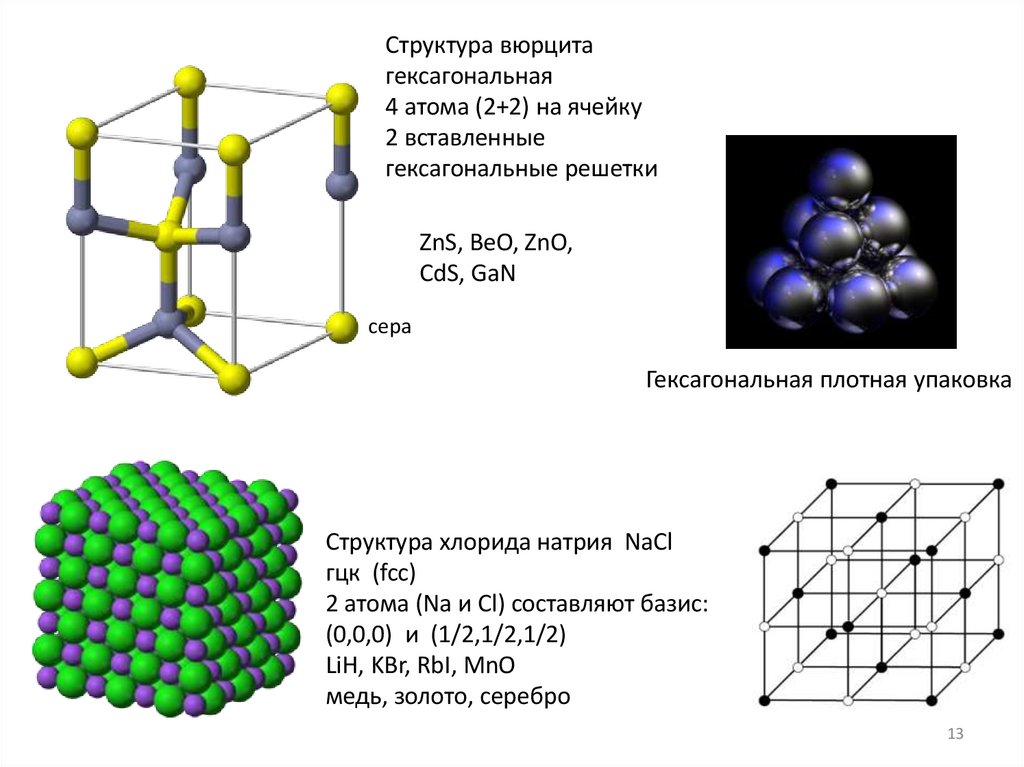
Структура вюрцита
гексагональная
4 атома (2+2) на ячейку
2 вставленные
гексагональные решетки
ZnS, BeO, ZnO,
CdS, GaN
сера
Гексагональная плотная упаковка
Структура хлорида натрия NaCl
гцк (fcc)
2 атома (Na и Cl) составляют базис:
(0,0,0) и (1/2,1/2,1/2)
LiH, KBr, RbI, MnO
медь, золото, серебро
13

14.

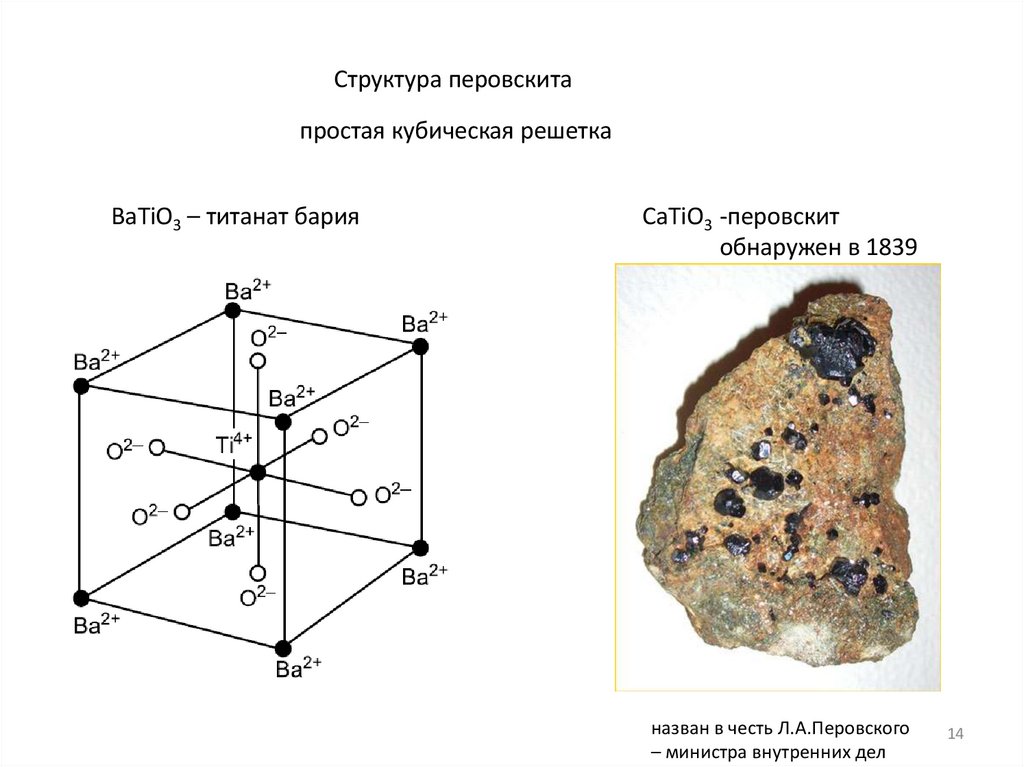
Структура перовскита
простая кубическая решетка
BaTiO3 – титанат бария
СaTiO3 -перовскит
обнаружен в 1839
назван в честь Л.А.Перовского
– министра внутренних дел
14

15.

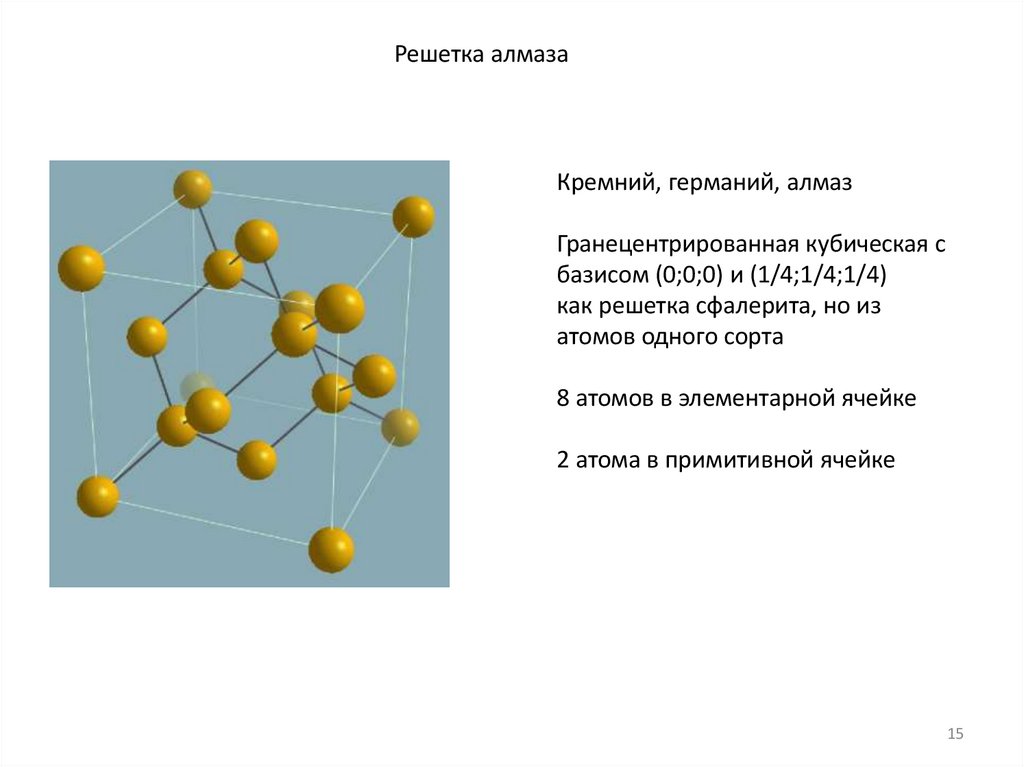
Решетка алмаза
Кремний, германий, алмаз
Гранецентрированная кубическая с
базисом (0;0;0) и (1/4;1/4;1/4)
как решетка сфалерита, но из
атомов одного сорта
8 атомов в элементарной ячейке
2 атома в примитивной ячейке
15

16.

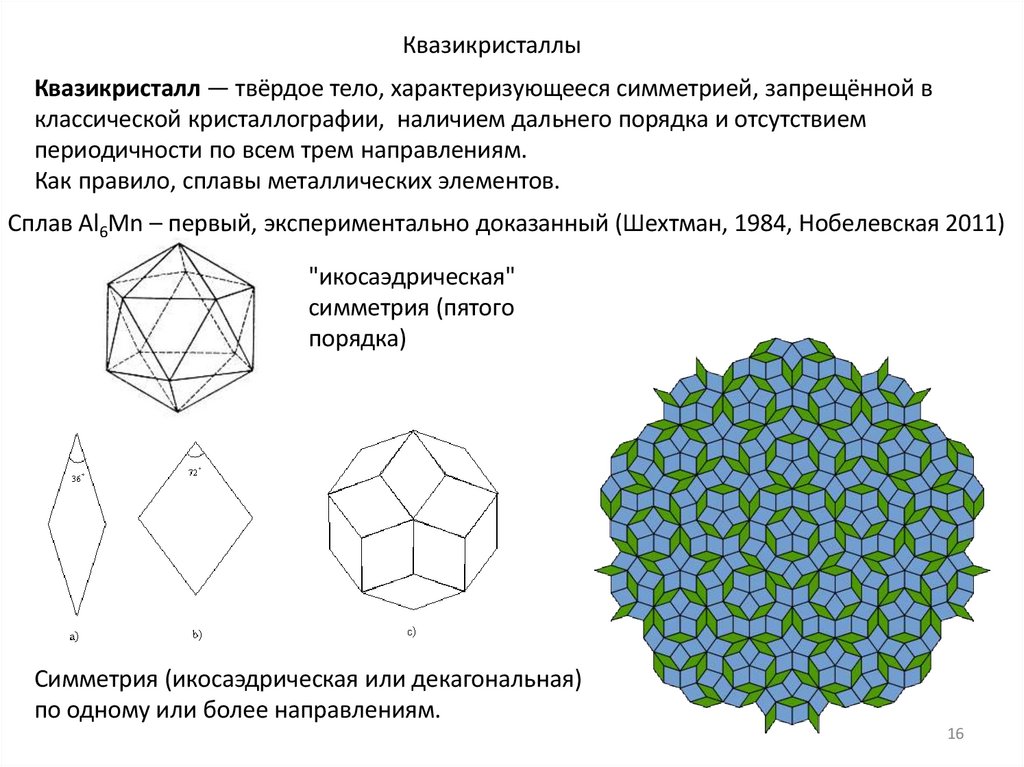
Квазикристаллы
Квазикристалл — твёрдое тело, характеризующееся симметрией, запрещённой в
классической кристаллографии, наличием дальнего порядка и отсутствием
периодичности по всем трем направлениям.
Как правило, сплавы металлических элементов.
Сплав Al6Mn – первый, экспериментально доказанный (Шехтман, 1984, Нобелевская 2011)
"икосаэдрическая"
симметрия (пятого
порядка)
Симметрия (икосаэдрическая или декагональная)
по одному или более направлениям.
16

17.

Обратная решетка
a1, a2, a3 - векторы элементарных трансляций
b1 2
a2 a3
a1 a2 a3
b1, b2, b3
b2 2
a3 a1
a2 a3 a1
b3 2
a1 a2
a3 a1 a2
- векторы элементарных трансляций обратной решетки
a1 a2 a3 - объем v примитивной ячейки прямой решетки
b1 b2 b3
- объем v* примитивной ячейки обратной решетки
v* 2 / v
3
ai bi 2 ...
R – вектор прямой решетки, B – вектор обратной решетки
eiBR 1
Размерность векторов B
17

18.

Обратная решетка для кубических решеток Браве
Для примитивной кубической решетки обратная решетка тоже примитивная
кубическая решетка
Для гранецентрированной кубической решетки обратная решетка объемноцентрированный куб и наоборот.
Обратная решетка для одномерного кристалла
b
2
a
Обратная решетка для двумерного кристалла
b2
! Отсутствующие
элементарные векторы
заменяются на векторы
нормалей к цепочке или
плоскости
Для квадратной решетки
b1
b1
2
a1
b2
2
a2
18

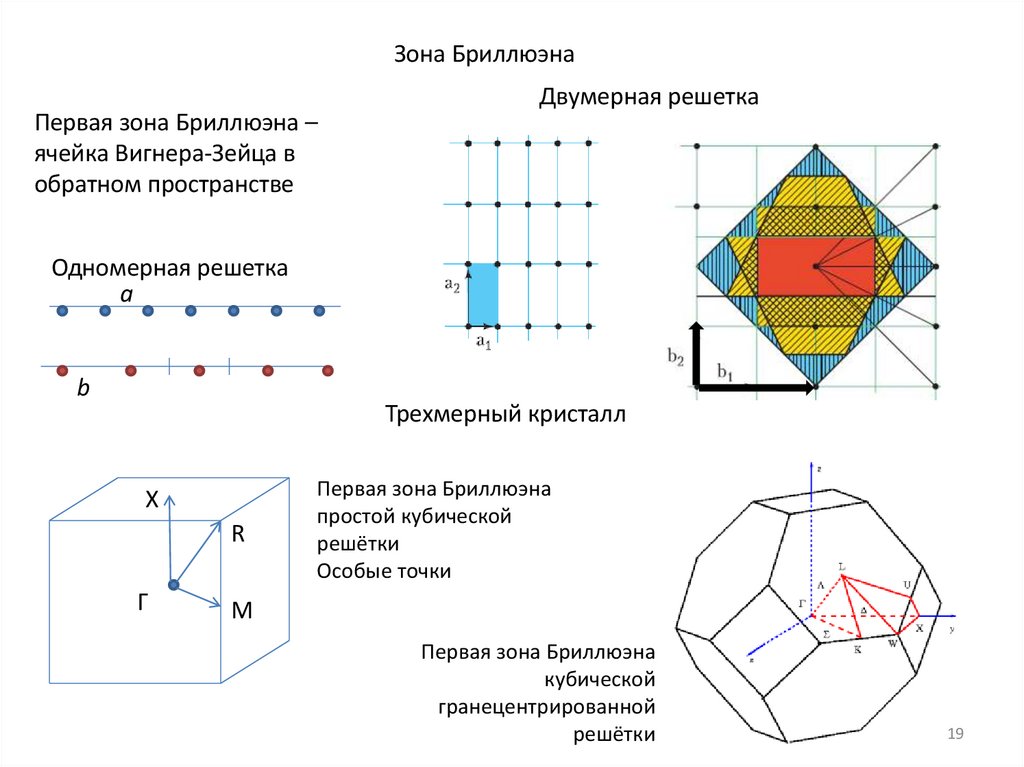
19.

Зона Бриллюэна
Первая зона Бриллюэна –
ячейка Вигнера-Зейца в
обратном пространстве
Двумерная решетка
Одномерная решетка
a
b
Трехмерный кристалл
X
R
Γ
Первая зона Бриллюэна
простой кубической
решётки
Особые точки
M
Первая зона Бриллюэна
кубической
гранецентрированной
решётки
19