Тема 2. Электронный энергетический спектр как фундаментальная характеристика твердого тела. Перестройка энергетического спектра

1. `

Тема 2.
Электронный энергетический
спектр как фундаментальная
характеристика твердого тела.
`
Перестройка энергетического
спектра под влиянием внешних
воздействий.

2.

Твердое тело - не есть совокупность
невзаимодействующих атомов
Разность энергии конфигурации атомов
образующих Тв. Тело по сравнению с
энергией системы из изолированных атомов
называется энергией связи.
Она варьируется от 0,1 эВ на атом,
в кристаллах, в которых атомы
связаны Ван дер Ваальсовским
взаимодействием до 7 эВ на атом
в ионных кристаллах.

3.

Типы междуатомных связей
Ван дер Ваальсово взаимодействие
A/r6
U = -A/r6 + B·exp(-r/ )
ограничения на
направления
образования связей
отсутствуют
Дипольный
момент
нулевых
колебаний
заряда

4.

Типы междуатомных связей
Ионная связь
Практически полная передача электрона
от аниона к катиону
Кулоновское взаимодействие
U = - e2 /r + B · exp(-r/ )
Энергетически наиболее
выгодная структура
кристалла определяется
соотношением между
радиусами аниона и катиона

5.

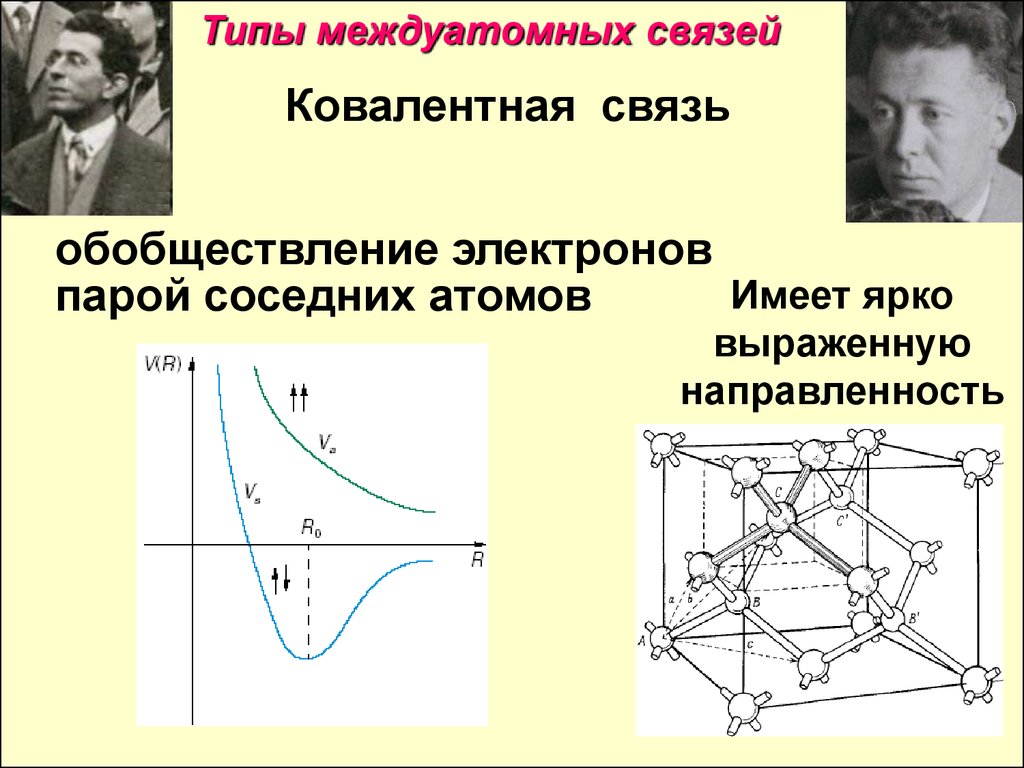
Типы междуатомных связей
Ковалентная связь
обобществление электронов
Имеет ярко
парой соседних атомов
выраженную
направленность

6.

Особенность кристаллов – периодичность
Весь кристалл можно построить на основе
решеток Браве
Решетка Браве, образована
всеми точками
с радиус-векторами
R n1a1 n2 a2 n3a3
где a1, a2, a3 вектора трансляции
n1, n2, n3 все возможные целые числа

7.

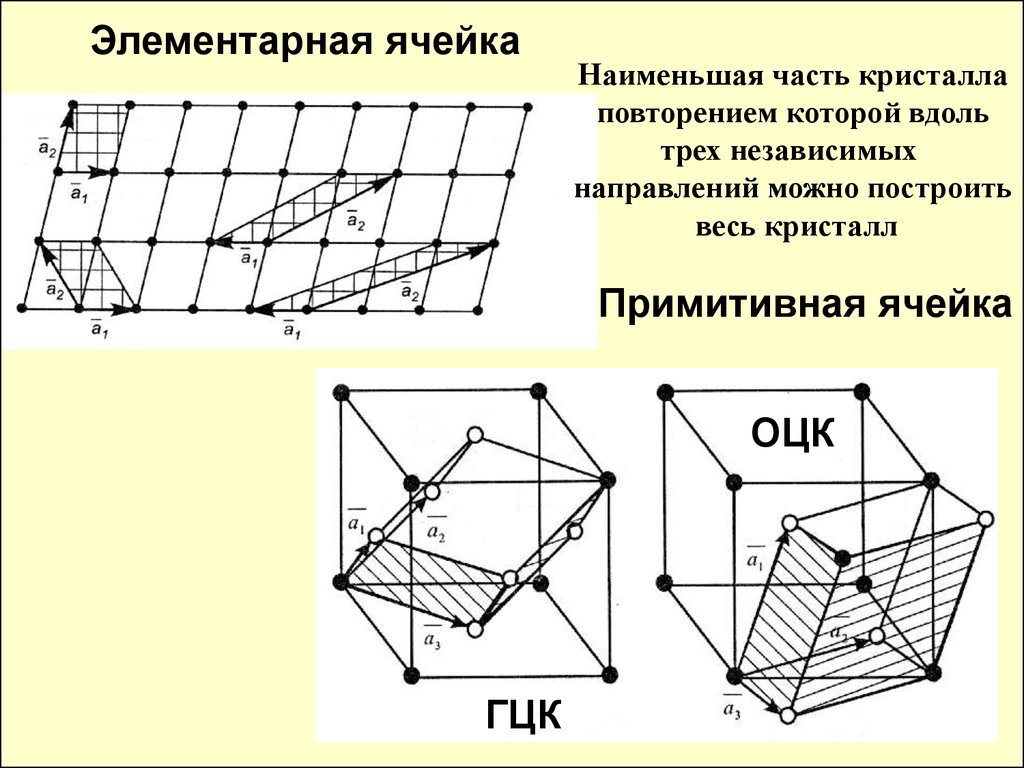
Элементарная ячейка
Наименьшая часть кристалла
повторением которой вдоль
трех независимых
направлений можно построить
весь кристалл
Примитивная ячейка
ОЦК
ГЦК

8.

Решетки Браве
7 кристаллических систем
1.
2.
3.
4.
5.
6.
7.
Триклинная
Моноклинная
Ромбическая
Тетрагональная
Гексагональная
Тригональная
Кубическая
a1 a2 a3;
a1 a2 a3; = = 90°
a1 a2 a3; = = =90°
a1 = a2 a3; = = =90°
a1 = a2 a3; = = 90° ; = 120°
a1 = a2 = a3; 120° > = = 90°
a1 = a2 = a3; = = =90°
Элементарная ячейка, 14 типов решеток
1.
2.
3.
4.
Примитивная
Объёмоцентрированная
Гранецентрированная
Базоцентрированная
7
4 (М,Р,Те,К)
2 (Р,К)
1 (Р)

9.

элементарные ячейки
Триклинная a
Моноклинные б, ж
Ромбические г, д, е, ж
Тетрагональные з,и
Гексагональная к
Тригональная л
Кубические м,н,о

10.

Элементарная ячейка – Вигнера - Зейтца
Двумерная
решетка
ОЦК
aR
ГЦК
2
R
2
0

11.

Индексы Миллера
x ma1
y na2
z pa3
Координаты узла [m,n,p]
Координаты направления <m,n,p>
Координаты плоскости (h,k,l)
Семейство плоскостей {h,k,l}

12.

Обратная решетка
R n1a1 n2 a2 n3a3
f (R)
2 [a a ]
2 [a3 a1 ]
2
3
b2
b1
(a2 [a3 a1 ])
( a1[a2 a3 ])
2 [a1 a2 ]
b3
(a1[a2 a3 ])
(a3 [a1 a2 ])
b q1b1 q2b2 q3b3 Вектор обратной решетки

13.

'
Дифракционный максимум
b
K
K
n
имеет место когда разность хода
волновых векторов падающей и рассеянной
волны равен вектору обратной решетки.
Это условие эквивалентно условию Вульфа Брэга
2 n
2d sin n
K

14.

Пример построения
обратной решетки
2
a
a1 ( h0 l0 )
b1
( h0 k0 l0 )
2
a
2
a
a2 ( h0 k0 )
b2
( h0 k0 l0 )
2
a
a
2
a3 ( k0 l0 )
b3
( h0 k0 l0 )
2
a
3
a
(a1[a2 a3 ])
4

15.

Зона Бриллюэна – Ячейка Вигнера Зейтца
в обратном пространстве
?
ГЦК
?
ОЦК

16.

Описание кристалла
ri координаты электронов R координаты ионов
Уравнение Шредингера для кристалла
e ( ri , R )
2me i
2M
2
2
2
(r , R )
i
1
e
( ri , R ) [W ( re , R ) U ( R )] ( ri , R )
2 j i ri rj
E ( ri , R )

17.

Адиабатическое приближение
2
2me
(ri , R ) (ri , R α ) ( R )
( R ) (r , R ) 2M (r , R ) ( R )
2
2M
2
e
i
i
i
2
( R )Δ α χ(ri , R α )
α χ(ri , R α ) ( R )
M
1
e2
( R ) (ri , R )
2 j i ri rj
[W (re , R ) U ( R )] ( R ) (ri , R ) E ( R ) (ri , R )
2 = ( )= ( + ) = 2 + 2 + 2

18.

Адиабатическое приближение
(ri , R α )
2
2me
Параметрическая зависимость от R
1
e2
(ri , R )
i e (ri , R ) 2
j i ri r j
W (re , R ) (ri , R ) N ( R ) (ri , R )
2
2M
(R )
[ N ( R ) U ( R )] ( R ) E ( R )
Координаты ядер полагаются постоянными и
равными своим средним значениям. R =const

19.

Адиабатическое приближение
Координаты ядер полагаются
постоянными и равными своим средним
значениям.
Одноэлектронное приближение
2
2
e j ( rj )
2
1
e
C
dri Хартри
ri rj
j i
2 j i ri rj
1 2 2
e
2m
(r) + [ (r) +U(r)] (r) = (r),
2
Для каждого электрона!!!!
2
j ( r1 ) e j ( r2 ) i ( r2 )
dr2
Хартри-Фок ex ( r1 ) ( r )
r2 r1
j
i
1

20.

Свободный электрон в бесконечном
пространстве
2
1 2
(r ) E (r )
2m
2
k (r ) 0
2
k2 = (2m·E) / 2
k = kx+ ky+ kz
Общее решение
(r) = A exp[i (kr - t)]
k = 2 / , p = k , E=
Длина волны Де Бройля

21.

(r) = A exp[i (pr -Et)/ ]
d 1 dE k
vгр
dk dk m
E
p 2 2k 2
E
2m 2m
Бесконечное вырождение!
E
E
E

22.

Lz
Ly
Lx
Модель Зоммерфельда!
Валентные электроны образуют
электронный газ, заключенный в
объёме V. Выберем куб, со стороной L.
Lx • Ly •Lz = V
Надо решить уравнение Шрёдингера
для свободных электронов 2 i / xi2+ k2 = 0
k2 = (2m·E) / 2
k = kx+ ky+ kz
из условий нормировки
Общее решение
2
A 2
V
Гран. Условия:
(r) = A exp[i (kr)]
x(0) = y(0)= z(0)=0
x(Lx) = y(Ly)= z(Lz)=0
exp[i kx Lx]= exp[i ky Ly)]= exp[i kz Lz] =0

23.

Решение удовлетворяющее гран.условиям
Стоячие волны
sin(kxLx)= sin(kyLy)= sin(kzLz)=0
kxLx= n1 kyLy = n2 kzLz= n3
k, принимает не любые, а дискретные значения
kx= n1 /Lx
ky= n2 /Ly
kz= n3 /Lz
Длина волны
x=2 /kx …….
2
2
2
n1 n2 n3
2
2
2
E
kx k y kz
2 2 2
2m
2m Lx Ly Lz
2
2
2

24.

Гран. Условия Кармана- Бора
При рассмотрении процессов переноса заряда
От стоячих волн удобно перейти к бегущим
Для этого надо изменить гран.условия на:
(x,y,z) = (x + Lx, y,z)
(x,y,z) = (x, y + Ly,z)
(x,y,z) = (x, y,z + Lz)
Дискретность решения по k сохранится!!!

25.

Движение свободного электрона
E = k2 2 / 2m
Движение электрона, локализованного в «ящике»
k, принимает не любые, а дискретные значения
kx= n1 /Lx
ky= n2 /Ly
kz= n3 /Lz
E = 2 ( kx2 + ky2 + kz2)/ 2m
Длина волны
x=2 /kx ……. << L

26.

Учет периодического потенциала
V (r ) V (r a )
2
1 2
e (r) + [ (r) +U(r)] (r) = (r),
2m
V ( r ) ( r ) U ( r )
Мы должны изучить свойства гамильтониана
с периодическим потенциалом

27.

Теорема Блоха
Собственные функции оператора Гамильтона
H
U ( r ), U ( r ) U ( r R),
2m
2
R n1a1 n2 a2 n3a3
где R любой вектор решетки Браве, могут быть
записаны в виде плоской волны, умноженной
на функцию с периодичностью решетки Браве:
n (r ) un (r ) e
un (r ) un (r R)
ik r
F.Bloch, Z.Physik, 52, 555 (1928)

28.

Примеры Блоховских функций
а

29.

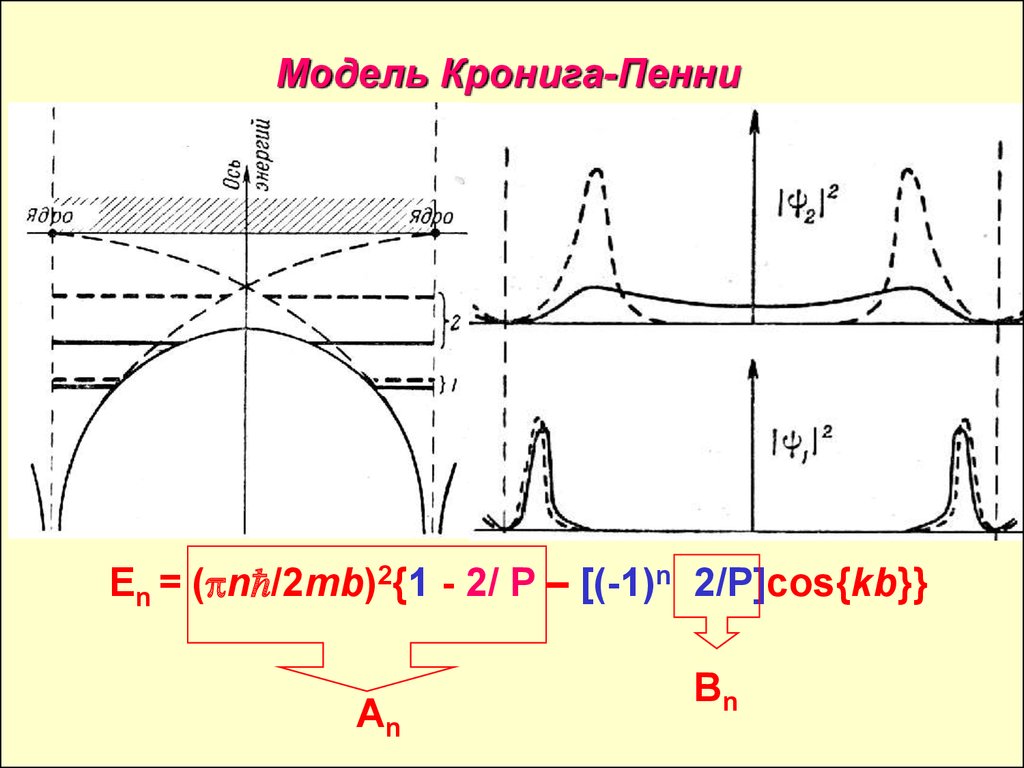
Образование энергетических
зон в модели Кронига-Пенни
Proc. R. Soc. Lond. A 3 130 (1931)
Ralph de
Kronig
William
Penney
V(x) = V(x+a) = V(x+2a)=….
I II
V( x) 0 для 0 x b
V( x) V0 для c x 0
d2 1(x)/dx2 + 2 1(x) = 0 I
d2 2(x)/dx2 + 2 2(x) = 0 II
d2 (x)/dx2 + {2·m / 2} [E- V(x)] (x) = 0
2=(2m·E) / 2 I; 2 = (2m·(V0 -E)) / 2 II
Хотим описать движение электрона в такой
системе, т.е. найти зависимость E(k)

30.

Модель Кронига-Пенни
Влияние периодичности потенциала на вид в.ф.
( x) u( x)e
ikx
u(x) = u(x+b+c)
( x b c) u( x b c)e
ik ( x b c )
( x)e
ik ( b c )
e ( x)
ika
После подстановки в.ф. в ур.Ш. Получаем систему ур.
d 2u1
du1
2
2
2
ik
k
u1 0, 0 x b
2
dx
dx
2
d u 2 2ik du 2 2 k 2 u 2 0, c x 0
2
dx
dx
Решение этой системы ур. имеет вид:
u1 (x) = Aei (
- k) x +
Be -i ( + k) x = e -i k x ( Aei x +Be-i x )
u2 (x) = Ce ( - ik) x + De - ( + ik) x = e -i k x ( Ce x + De - x )

31.

Модель Кронига-Пенни
1(x) = Aei x + Be -i x 0 x b
2(x) = Ce x + De - x -c x 0
Граничные условия на в.ф.
ika
b
b
c
a
c
e
1 0 2 0
1
2
2
2
ika
b
c
e
0
0
2
1
2
1
Подстановкой гран.условий получаем систему ур.
A + B- C –D = 0
i A - i B- C + D = 0
Aei b + Be-i b - C e- ceika -D e ceika = 0
i Aei b - i Be-i b - C e- ceika+ D e ceika = 0

32.

Модель Кронига-Пенни
1
i
i b
e
i e
i b
1
i
i b
e
i e
i b
1
c ika
e e
c ika
e e
1
c ika
e e
0
c ika
e e
cos(ka) = {( 2- 2)/2 } sh( c) sin( b) + ch( c)cos( b)
Подставим в ур. 2=(2m·E) / 2 ; 2 = (2m·(V0 -E)) / 2
2mE 2m V0 E
V0 2 E
sin b
sh c
2
2
2 (V0 E ) E
2mE 2m V0 E
cos b
ch c
cos k b c
2
2

33.

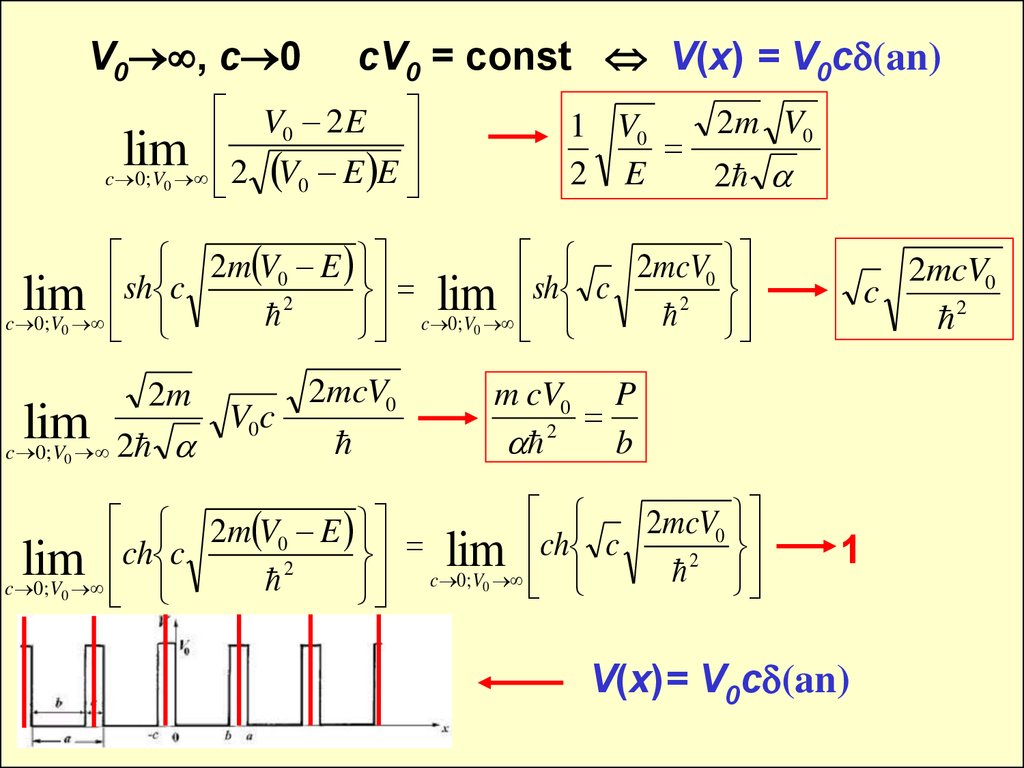
V0 , c 0
cV0 = const V(x) = V0c (an)
V0 2 E
lim
c 0; V0
2 V0 E E
2m V0
1 V0
2 E
2
2m V0 E
2mcV0
sh c
lim sh c
lim
2
2
c 0; V0
c 0;V0
2mcV0
2m
V0c
lim
c 0; V0 2
2mcV0
c
2
m cV0 P
2
b
2mcV0
2m V0 E
lim ch c
ch
c
2
lim
2
c 0; V0
c 0; V0
1
V(x)= V0c (an)

34.

2mE 2m V0 E
V0 2 E
sin b
sh c
2
2
2 (V0 E ) E
2mE 2m V0 E
cos b
ch c
cos k b c
2
2
V(x)=V0c (an)
m cV0b
P
2
2mE
2
cos{kb} = {P/ b } sin{b } + cos{ b }
Получили закон дисперсии –
уравнение, связывающее Е с k

35.

cos{kb} = {P/ b } sin{b } + cos{ b }
b = b(2m·E)0.5 /
1 cos{kb} -1
P 0
V0c 0
b = kb
E = k2 2 /2m
( x) u( x)e
ikx
Для мнимого k, экспоненциально затухает!!!

36.

2a / = n
ka = n
a = n /2
k = 2 / 2 a / = n
Переход к запрещенной зоне при cos{ka}= 1
2a sin = n
Условие Вульфа-Брэггов при нормальном = /2
падении волн на кристаллограф. плоскость.
Т.е. электрон с , удовлетворяющей этому
условию НЕ может двигаться в кристалле.

37.

Модель Кронига-Пенни
cos{kb} = {P/ b } sin{b } + cos{ b }
P
V0c электрон сильно связан в яме
P sin{b } 0 b n
P>>1 b = n + o(b )
cos{kb} = {P/ n } sin{ n + o(b )} + cos{ n + o(b )}
sin{ n + o(b )} = sin{ n} + cos{ n}·( n+o(b ) - n)
= (-1)n o(b )
cos{ n+o( )} =cos{ n}+ sin{ n}·( n+o(b )- n) =(-1)n
(-1) n{1+[P/ n] o(b ) } = cos{kb}
o(b ) = -[ n/P](1+(-1)n cos{kb})

38.

Модель Кронига-Пенни
b = n + o(b )
o(b ) = -[ n/P](1+(-1)n cos{kb})
b = n - [ n/P](1+(-1)ncos{kb})= n(1-1/P- [(-1)n/P]cos{kb})
b(2m·E)0.5 / = n {1 - 1/ P – [(-1)n /P]cos{kb}}
En = ( n /2mb)2{1 - 1/ P – [(-1)n /P]cos{kb}}2
при P
En = ( n /2mb)2{1 - 2/ P – [(-1)n 2/P]cos{kb}}
An
Bn

39.

Для ограниченного кристалла
k = n /L, где n=0,1……N т.е. принимает N значений
и лежит в переделах 2 /a k 0
т.е. В каждой зоне N дискретных состояний
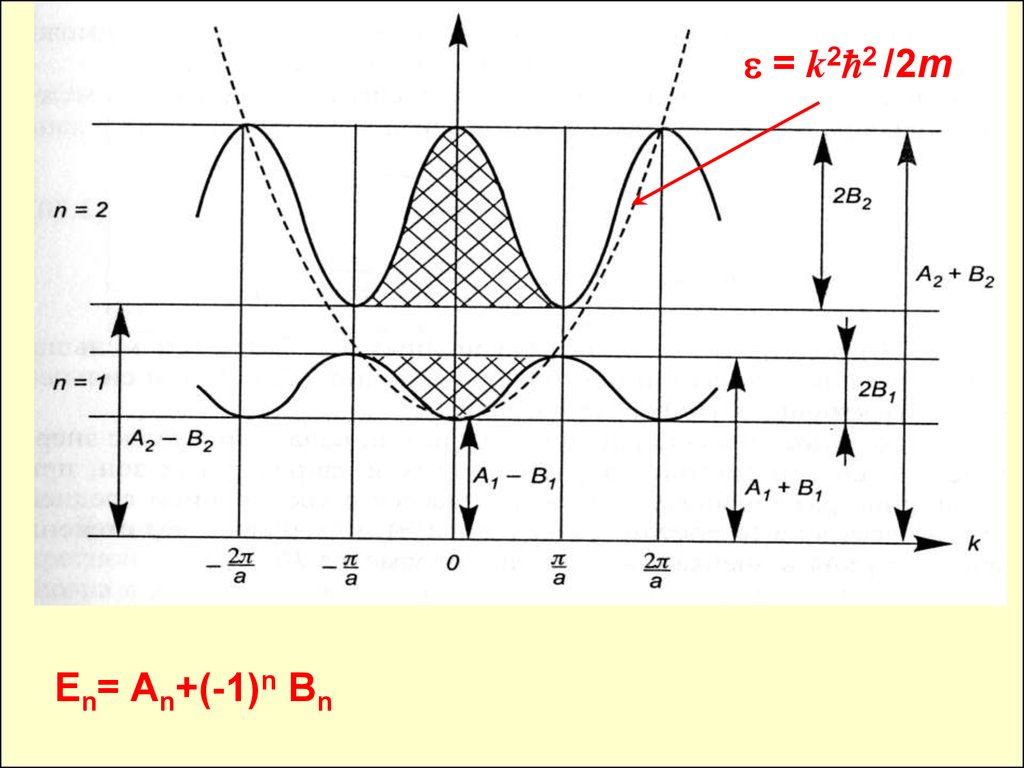
En= An+(-1)n Bncos{ka} Emax= An + Bn Emin= An - Bn
Ширина зоны: E = Emax - Emin
An = ( n /2ma)2(1 - 2/ P)
Bn = ( n /2ma)2(2/ P)
En = 2 Bn = ( n /2ma)2(4/ P)
Выбор промежутка изменения k не однозначен,
обычно выбирают /a k - /a

40.

= k2 2 /2m
En= An+(-1)n Bn

41.

В разных направлениях движения
электрона разная ширина зон!!!!
GaAs

42.

Эффективная масса
Разложим функцию E(k) в близи края зоны в ряд
E(k) = E(k0)+ 0.5 [ 2E(k)/ k k ](k - k0) (k - k0)+…
Выберем начало отсчета E(k0)=0 и k0 =0
Можно ввести тензор 1/m = [1/ 2 ] 2 (k)/ k k
Приведем тензор к главным осям
1/m = [1/ 2 ] 2 (k)/ k 2
Тогда E(k) =0.5 2k 2 /m
E(k) = p
2 /2m
p= k
E(k) = p2 /2m*

43.

Эффективная масса
2
1
1 d E (k )
2
2
m dk
2
k
k
kz
E
2 m|| m m
2
2
x
2
y

44.

Зонная диаграмма Si
Зонная диаграмма Ge

45.

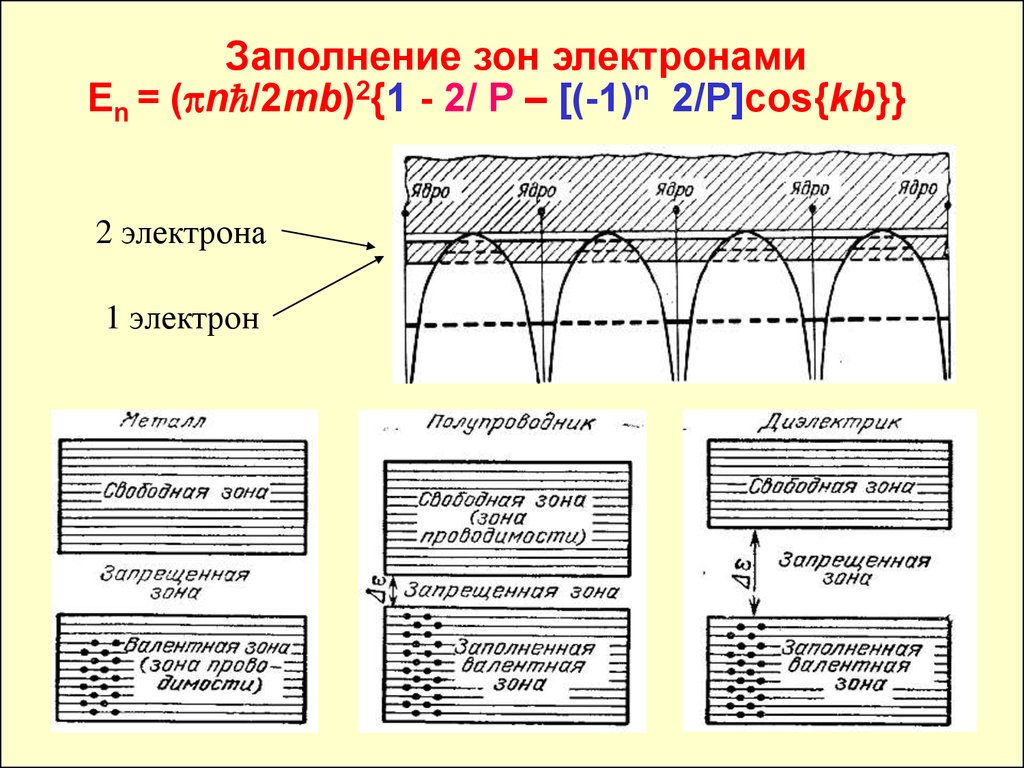
Заполнение зон электронами
En = ( n /2mb)2{1 - 2/ P – [(-1)n 2/P]cos{kb}}
2 электрона
1 электрон

46.

Заполнение зон электронами
f ( )
1
1 e
n
Emax
g
(
E
)
f
(
E
,
T
)
dE
Emin
F
kT

47.

Плотность состояний
Плотность состояний g(E) - число состояний в
единичном интервале вблизи заданной энергии
Полное число состояний
dG ( E )
dpx dp y dpz dxdydz
2
3
E dE
E
G( E ) dV
V
G( E )
pmax
0
pmax
0
3
dVd p
3
2
3
d p
3
2
В единице
объема
3
d p
3
2
dG ( E )
g (E)
dE

48.

Плотность состояний сферическая
изоэнергетическая поверхность
pmax
3
d p d 3 p 4 p 2 dp
G( E ) 2
3
0 2
3
pmax
2
4 p dp 8 p max
G( E ) 2
3
3
2 3 [2 ]
0
2
p
E ( p) Ec
p 2m( E ( p) Ec )
2m
3
3/ 2
p
max
[2m( E Ec )]
8
G( E )
3
2 3
3 [2 ]
3
3/ 2
2m
( E Ec )
dG( E )
g (E)
2 3
dE

49.

Положительные дырки
ev J e v
Je
n
s
S s
S
Для заполненной
зоны Jn=0
vs 0
s
удалим из заполненной зоны один электрон
evi
e evi
Jn
vs (
)
S s
S
S
т.е. ток равен току одного электрона с зарядом +e
В почти заполненной зоне
e
J p vs
S s

50.

Перестройка энергетического
спектра под влиянием:
Давления
Температуры
Легирования
Электрического поля
Магнитного поля

51.

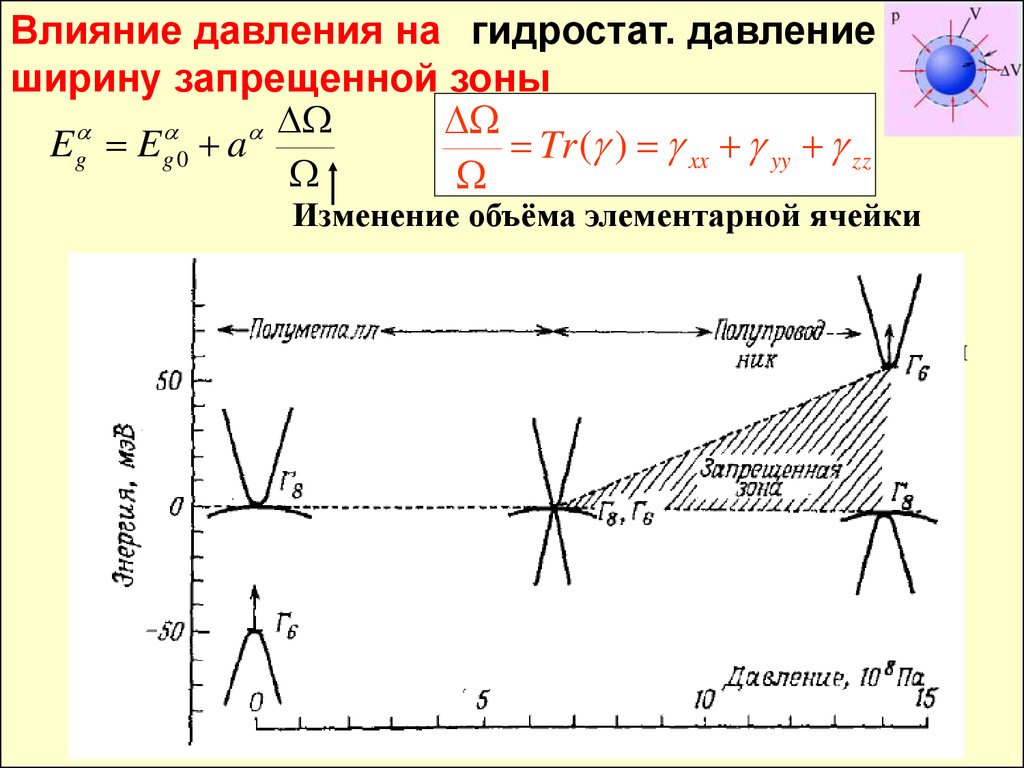
Влияние давления на гидростат. давление
ширину запрещенной зоны
Eg Eg 0 a
Tr ( ) xx yy zz
Изменение объёма элементарной ячейки
В общем случае под действием механического напряжения
зонная структура изменяется - происходит сдвиг краев зон, и
в случаях, когда возмущение понижает симметрию, - снятие
вырождения.
Изменение энергий описывают с использованием тензора
потенциалов деформации.
Для кубических кристаллов число независимых компонент
тензора потенциала сводится к трем. В особых точках зоны
Бриллюэна (Г,X и L) симметрия долин уменьшает число
компонент до двух.

52.

Влияние давления на ширину запрещенной
зоны GaAs E g E g 0 a
a , a L 0 ; a X 0

53.

Влияние давления на структуру запрещенной зоны
«Одно, двух осное давление»
E(n,l,m,s)
Состояния с различным l
(sharp)
s
0
(principal)
p
1
(diffuse)
d
2
(fundamental)
f
3

54.

Влияние давления на структуру запрещенной зоны
Одно,двуосное давление - расщепление вырожденных зон
Ehh-hl
E
2
E
4
E
2
2
4
2
9
E001 2b( zz xx )
E111 2 3d xy
2 E2 ( zz xx )
X XY
3
E2 ( zz xx )
X Z
3
L1 11
2 E3 xy
3
L111 2 E3 xy

55.

Влияние температуры на ширину
запрещенной зоны
Eg = Eg(0) - ·T2/(T+ )
Сглаживание периодического
потенциала
Тепловое расширение, обусловленное ангармонизмом
колебаний. т.е. Изменение энергетической щели из-за ее
зависимости от постоянной решетки.
Eg=1.519 - 5.405·10-4·T2/(T + 204) (eV), GaAs
Eg = 1.17 - 4.73·10-4·T2/(T + 636) (eV), Si

56.

Примеси в полупроводниках - феноменология
Появление состояний в запрещенной зоне
Донор – отдает электрон
в зону проводимости.
E Eg ED
E Eg E A
Акцептор – захватывает
электрон из валентной зоны
D
Захват электрона эквивалентен выбросу дырки
центр захвата для электронов
A центр захвата для дырок
D0 центр захвата для дырок
A0
центр захвата для электронов

57.

Влияние легирования на энергетический
спектр полупроводника
"Глубокие"
примесные уровни
"Мелкие" примесные уровни

58.

Энергетическая структура мелких
примесных уровней
aБ
2
e 2 m*
e 4 m*
m*
E 2 2 13,6
эВ
2
2
m0
Перекрытие состояний отдельных примесей
Примесные зоны

59.

Заполнение примесных зон носителями
«Хвосты» плотности состояний –
эффективное сужение запрещенной зоны

60.

Влияние сильного легирования на
энергетический спектр полупроводника
Заполнение зон носителями заряда
Эффект Бурштейна-Моccа

61.

Энергетический спектр в электрическом поле
Стационарные состояния электрона в эл. поле
Добавка к потенциальной энергии - eEz
= (p)+ eEz т.е. зоны должны наклониться
Это справедливо и для неоднородного эл.поля
когда масштаб изменения поля >> e

62.

Между зонные переходы!
Запрещенной зоне соответствуют значения
энергии с мнимым k
Туннельные переходы S ~ exp(- /E)
= Eg3/2mr1/2/2 e
mr= me mh / (me + mh)
Эффект Франца-Келдыша

63.

Энергетический спектр в магнитном поле
2
1p
[
U ] ( r ) E ( r )
2 m
без поля
e
В магнитном поле: p p A U U U
c
Энергия спина в поле
e
U g B ( , B) B 2m c ; матрицы Паули
0
1
e 2
( p A) g B ( , B ) E
2m
c

64.

1
e 2
H
( p A) g B ( , B )
2m
c
2
e 2
e
e
e
2
( p A) ( ) A i i A A
c
c
c
c
A i i A i div A
e 2
e
e
2
( p A) ( ) i ( 2 A div A) A
c
c
c
Кулоновская калибровка: divA=0, = 0
Выберем B (0,0, Bz )
B rot A(r )
Az Ay 0 ; Ax yBz yB
2

65.

Нет явной зависимости коэффициентов от x и z
eB
f ( y) c
Ищем решение в виде: e
mc
2
2
( )
e
d
1 eBy
H
i
yB
g B ( , B )
2m
mc
dx 2m c
2
( )
d m
2
H
i y c c y g B ( , B )
2m
dx 2
i (kx x kz z )
Получаем два уравнения, для разных проекций спина
2
2
d f
c k x
2
2
2 (k z k x ) f ) y y o y
2m
dy
eB
m
2
( y c k x c y g B ( , B) E ) f 0
2

66.

d f ( ) m c
f ( )
2
2m dy
2
2
2
2
2
2
2
z
k
( E
g B ( , B)) f ( )
2m
Уравнение для осциллятора!!!
2 2
z
k
1
E
g B ( , B)) c (n )
2m
2
Полная энергия электрона в поле
f
Hn (
y y0
)
e
1 y y 2
0
2
c
Be
Магнитная длина

67.

Энергетический спектр в магнитном поле
c kT
Спектр электрона в
отсутствие
магнитного поля
c
1 Ly Lx
m c Ly Lx
2
2 2
eB
Ly Lx
2 ñ
Кратность вырождения

68.

Влияние химической природы атомов
на зонную структуру.