10-Special theory of relativity

1. Специальная теория относительности

ВоГУ
Лекция 10
Специальная
теория
относительности
2019 г.
1

2. 1. Введение (предыстория вопроса) 2. Постулаты СТО 3. Преобразования Лоренца 4. Следствия из преобразований Лоренца 4.1.

План
1. Введение (предыстория вопроса)
2. Постулаты СТО
3. Преобразования Лоренца
4. Следствия из преобразований Лоренца
4.1. Относительность одновременности
4.2. Замедление времени
4.3. Сокращение длины
4.4. Интервал
4.5. Релятивистский закон сложения скоростей
5. Динамика СТО
5.1. Энергия покоя
5.2. Полная энергия; импульс
5.3. Кинетическая энергия
5.4. Фотоны. Неаддитивность массы
5.5. Второй закон Ньютона в СТО
6. Понятие об ОТО
2

3.

Предыстория вопроса: проблема эфира
Около 1865 г. Джеймс Клерк Максвелл создал теорию электромагнитного
поля (уравнения Максвелла).
Теория Максвелла предсказывала существование электромагнитных
волн, которые должны распространяться с некоторой фиксированной
скоростью с=3.108 м/с.
Возникал вопрос: относительно чего измеряется эта фиксированная
скорость?
Пришлось предположить существование некой субстанции, названной
«эфиром», которой наполнено все, даже «пустое» пространство.
Световые волны распространяются в эфире так же, как звуковые в
воздухе. Их скорость – это скорость относительно эфира.
Эфир – это абсолютная система отсчёта
3

4.

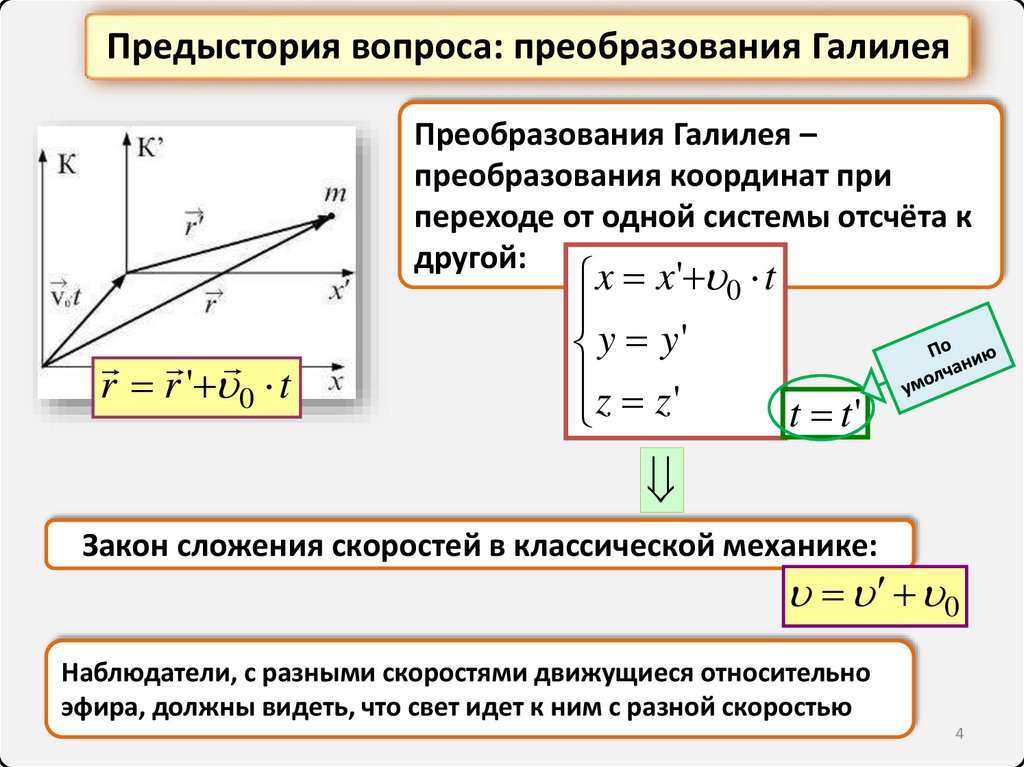
Предыстория вопроса: преобразования Галилея
Преобразования Галилея –
преобразования координат при
переходе от одной системы отсчёта к
другой:
r r ' 0 t
x x' 0 t
y y'
z z'
t t'
Закон сложения скоростей в классической механике:
0
Наблюдатели, с разными скоростями движущиеся относительно
эфира, должны видеть, что свет идет к ним с разной скоростью
4

5.

Опыт Майкельсона и Морли
1887 г.
Сравнивалось значение скорости света, измеренной
в направлении орбитального движения Земли, с её значением,
измеренным в перпендикулярном направлении.
vЗемли =3.104м/с
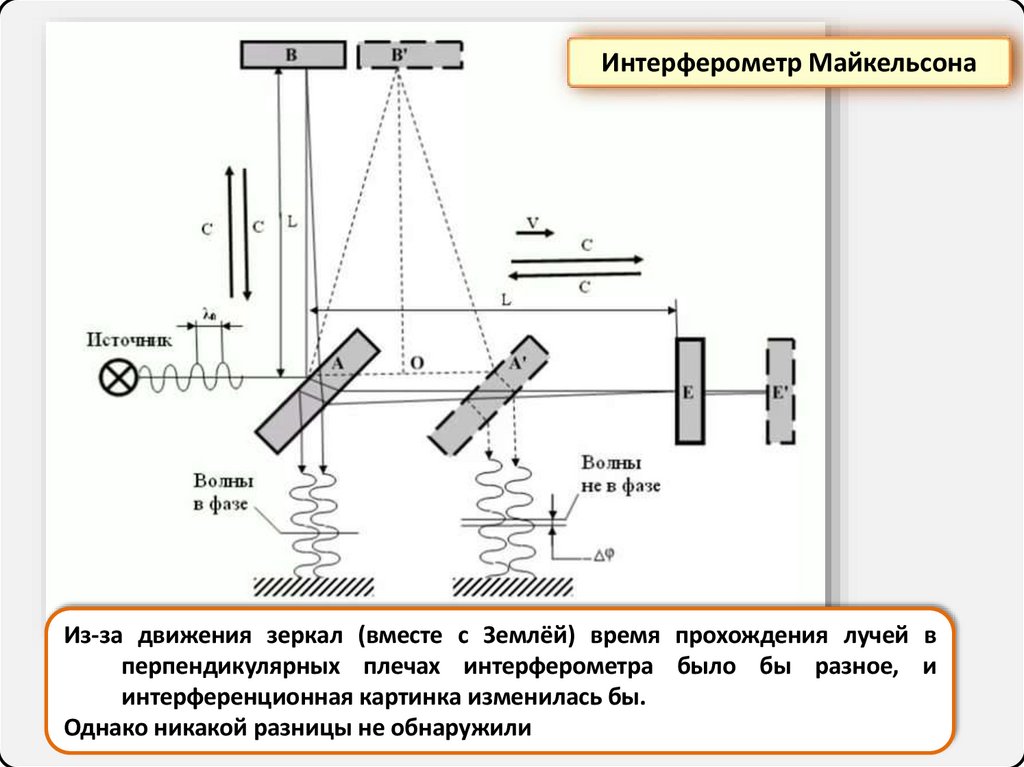
Интерферометр Майкельсона
Эдвард Уильямс
Морли
Альберт Абрахам
Майкельсон

6.

Интерферометр Майкельсона
Из-за движения зеркал (вместе с Землёй) время прохождения лучей в
перпендикулярных плечах интерферометра было бы разное, и
интерференционная картинка изменилась бы.
Однако никакой разницы не обнаружили

7.

1905 г.
Постулаты СТО
Альберт Эйнштейн
Публикация работы
«К электродинамике движущихся сред»,
в которой было показано,
что никакого эфира не нужно, если отказаться
от понятия абсолютного времени
1) Принцип относительности
Все законы природы одинаковы во всех инерциальных системах отсчёта.
Никакими физическими опытами нельзя установить, находится ли система
в покое или движется равномерно и прямолинейно
2) Принцип постоянства скорости света
Скорость света в вакууме одинакова во всех инерциальных системах
отсчёта, независимо от движения источника или наблюдателя

8.

x' 0 t
x
2
1 02
с
y y '
z z'
t ' 0 x
t
с2
2
1 02
с
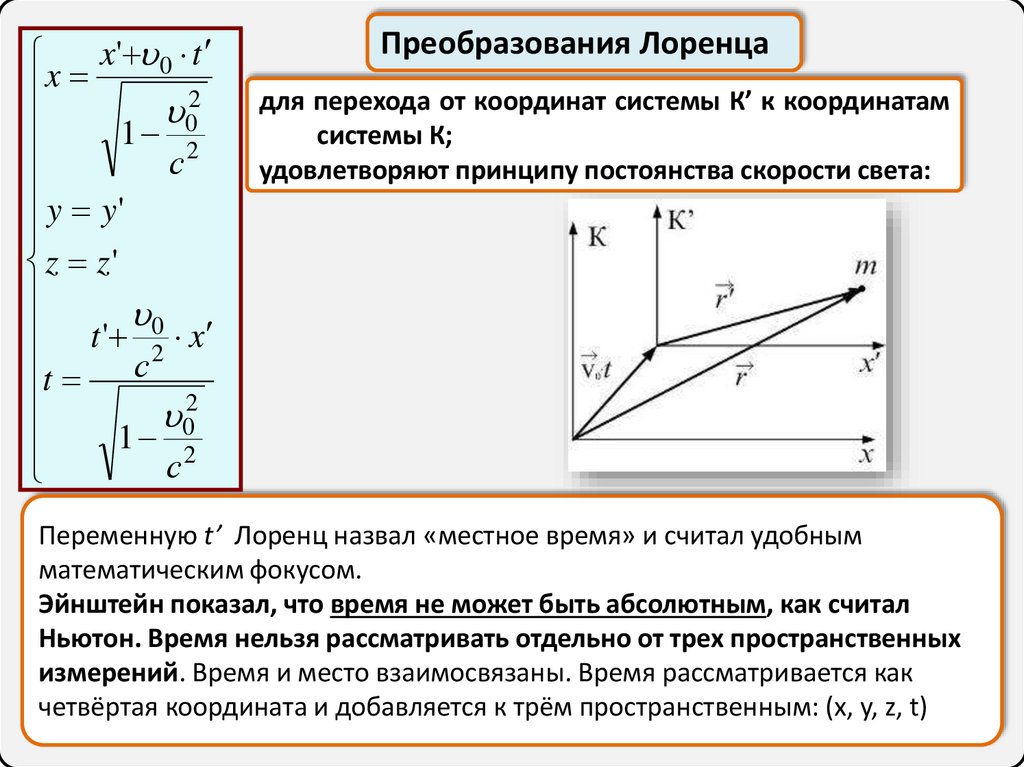
Преобразования Лоренца
для перехода от координат системы К’ к координатам
системы К;
удовлетворяют принципу постоянства скорости света:
Переменную t’ Лоренц назвал «местное время» и считал удобным
математическим фокусом.
Эйнштейн показал, что время не может быть абсолютным, как считал
Ньютон. Время нельзя рассматривать отдельно от трех пространственных
измерений. Время и место взаимосвязаны. Время рассматривается как
четвёртая координата и добавляется к трём пространственным: (x, y, z, t)

9.

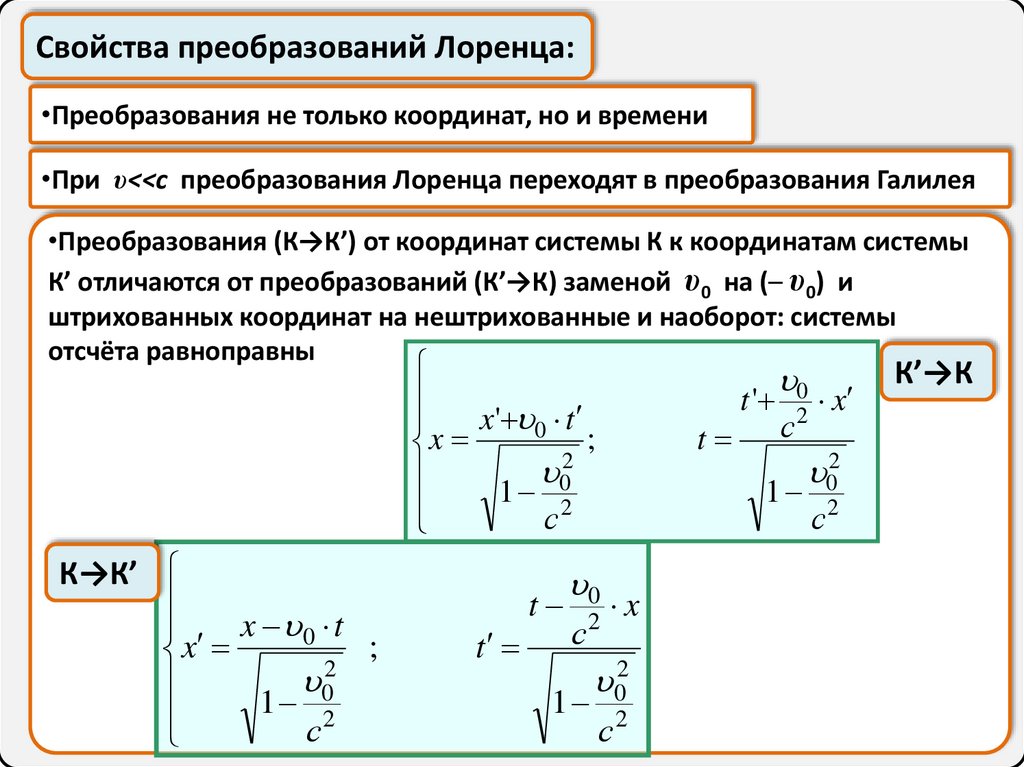
Свойства преобразований Лоренца:
•Преобразования не только координат, но и времени
•При υ<<c преобразования Лоренца переходят в преобразования Галилея
•Преобразования (К→К’) от координат системы К к координатам системы
К’ отличаются от преобразований (К’→К) заменой υ0 на (– υ0) и
штрихованных координат на нештрихованные и наоборот: системы
отсчёта равноправны
x' 0 t
x
;
02
1 2
с
К→К’
x 0 t
;
x
2
0
1 2
с
t
t
0
t ' 2 x
с
t
1
0
с
2
1
x
02
с2
02
с2
К’→К

10.

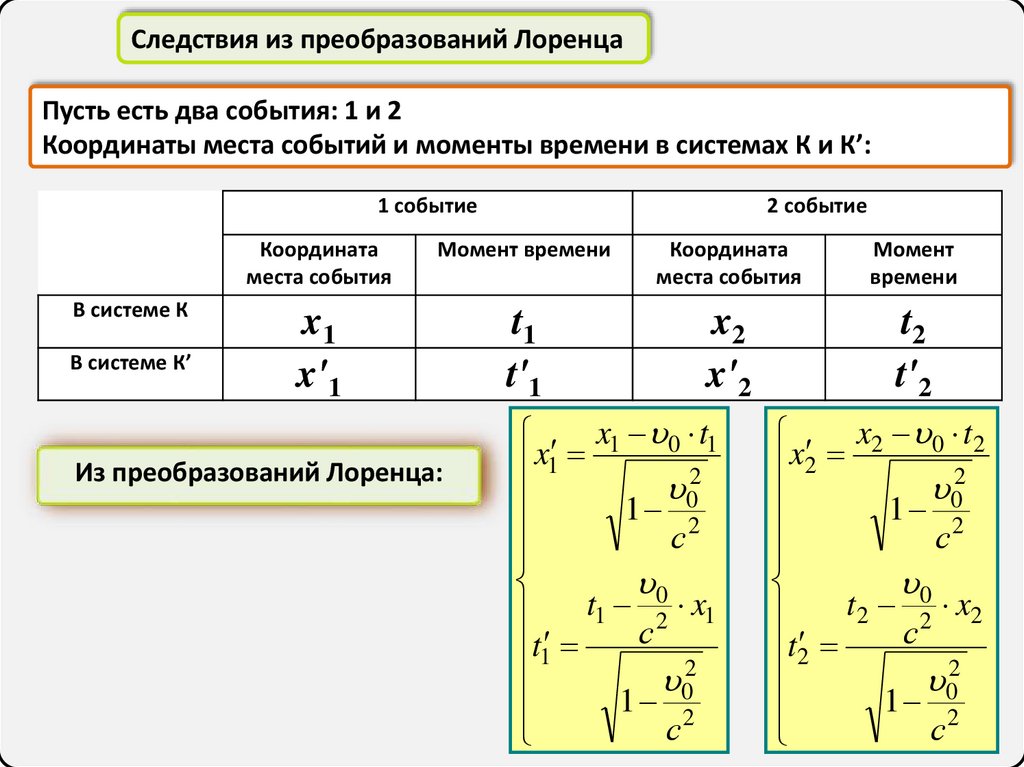
Следствия из преобразований Лоренца
Пусть есть два события: 1 и 2
Координаты места событий и моменты времени в системах К и К’:
1 событие
В системе К
В системе К’
2 событие
Координата
места события
Момент времени
Координата
места события
Момент
времени
x1
x'1
t1
t'1
x2
x'2
t2
t'2
Из преобразований Лоренца:
x1 0 t1
x1
2
1 02
с
0
t
x1
1
2
с
t1
02
1 2
с
x2 0 t2
x2
2
1 02
с
0
t
x2
2
2
с
t2
02
1 2
с

11.

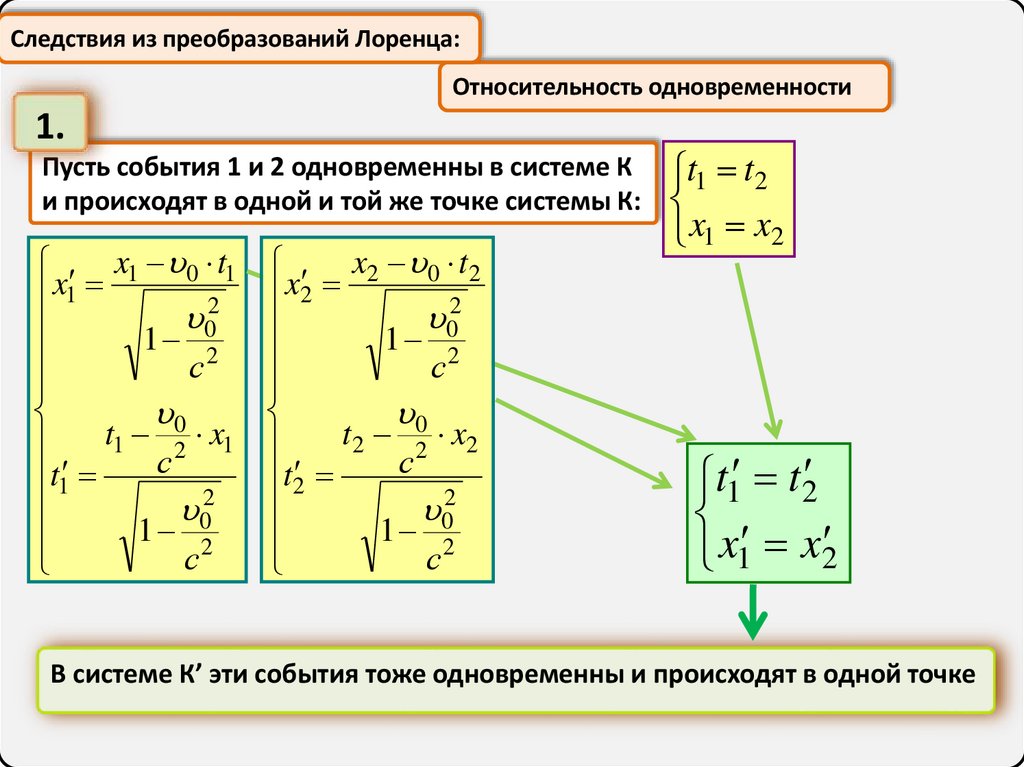
Следствия из преобразований Лоренца:
Относительность одновременности
1.
Пусть события 1 и 2 одновременны в системе К
и происходят в одной и той же точке системы К:
x1 0 t1
x1
2
1 02
с
0
t1 2 x1
с
t1
02
1 2
с
x2 0 t2
x2
2
1 02
с
0
t2 2 x2
с
t2
02
1 2
с
t1 t2
x1 x2
t1 t 2
x1 x2
В системе К’ эти события тоже одновременны и происходят в одной точке

12.

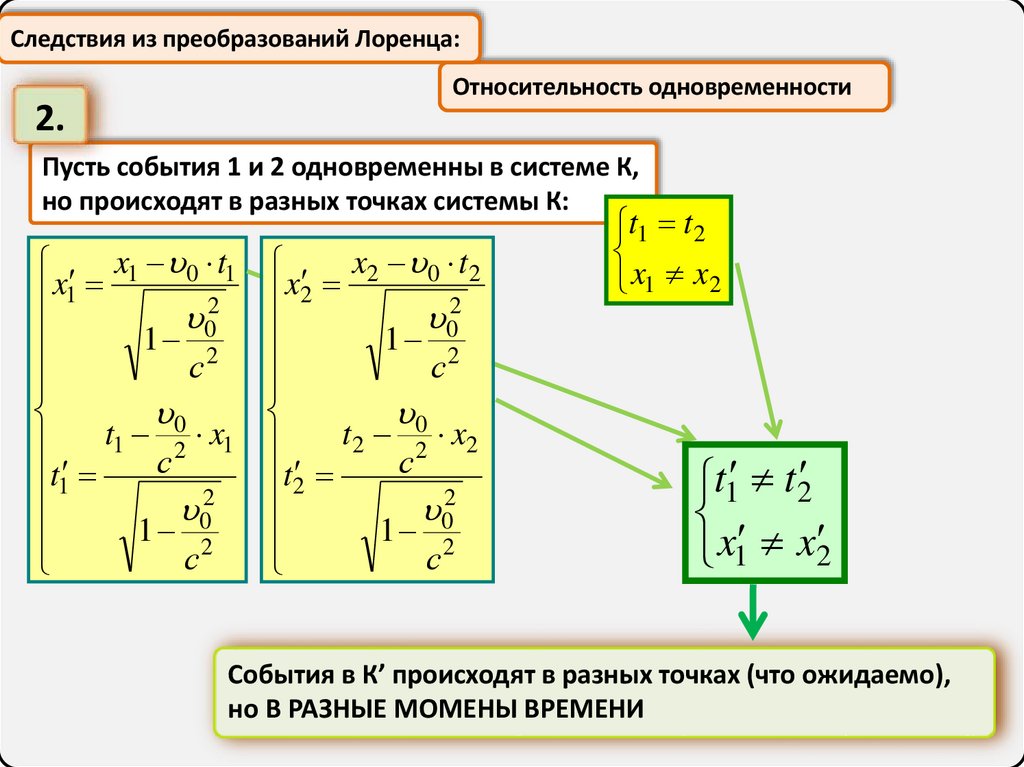
Следствия из преобразований Лоренца:
Относительность одновременности
2.
Пусть события 1 и 2 одновременны в системе К,
но происходят в разных точках системы К:
x1 0 t1
x1
2
1 02
с
0
t1 2 x1
с
t1
02
1 2
с
x2 0 t2
x2
2
1 02
с
0
t2 2 x2
с
t2
02
1 2
с
t1 t 2
x1 x2
t1 t 2
x1 x2
События в К’ происходят в разных точках (что ожидаемо),
но В РАЗНЫЕ МОМЕНЫ ВРЕМЕНИ

13.

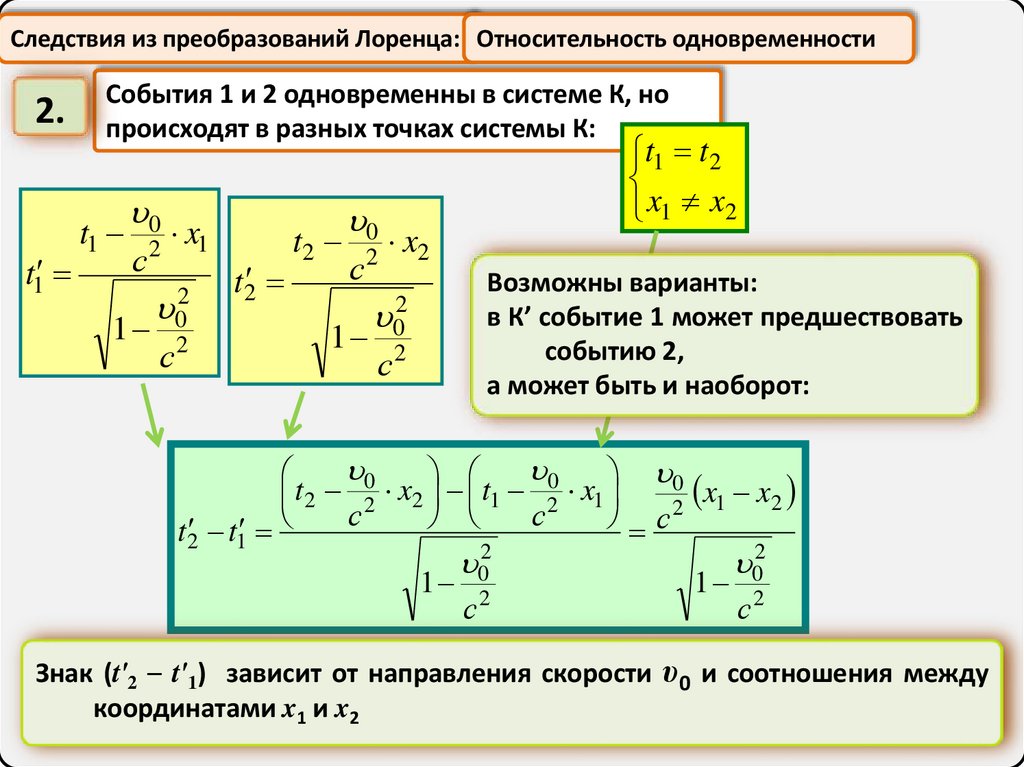
Следствия из преобразований Лоренца: Относительность одновременности
2.
t1
События 1 и 2 одновременны в системе К, но
происходят в разных точках системы К:
t1
0
с
x1
2
02
1 2
t2
с
t2
0
с
2
t1 t 2
x1 x2
x2
Возможны варианты:
в К’ событие 1 может предшествовать
событию 2,
а может быть и наоборот:
02
1 2
с
0
0
0
t
x
t
x
x x2
2
2 1
1
2
2
2 1
с
с
с
t t
2
1
1
02
с
2
1
02
с2
Знак (t'2 – t'1) зависит от направления скорости υ0 и соотношения между
координатами x1 и x2

14.

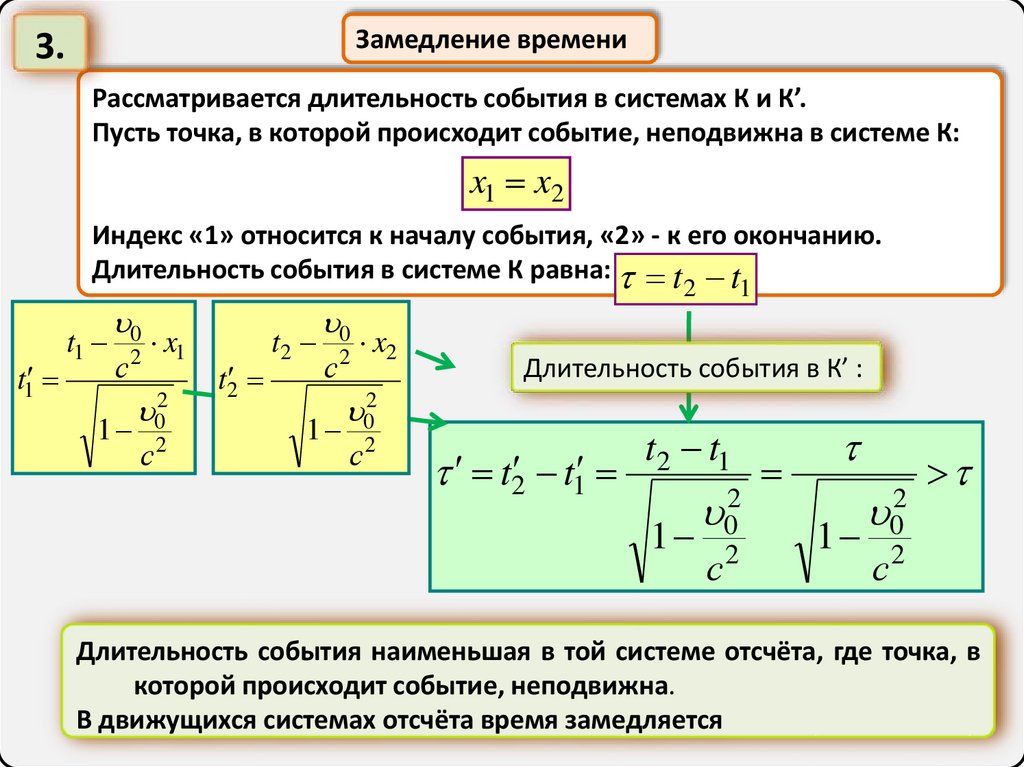
Замедление времени
3.
Рассматривается длительность события в системах К и К’.
Пусть точка, в которой происходит событие, неподвижна в системе К:
x1 x2
Индекс «1» относится к началу события, «2» - к его окончанию.
Длительность события в системе К равна: t t
t1
t1
0
с
x1
2
1
02
с
2
t2
t2
0
с
2
1
2
x2
Длительность события в К’ :
02
с2
1
t2 t1
t2 t1
1
02
с
2
1
02
с2
Длительность события наименьшая в той системе отсчёта, где точка, в
которой происходит событие, неподвижна.
В движущихся системах отсчёта время замедляется

15.

3.
Экспериментальная проверка замедления времени:
На высоте 10 км под действием космических лучей рождаются
короткоживущие частицы - µ-мезоны.
Их время жизни τ0 =2.10-6 с
Даже двигаясь почти со скоростью света, за это время частица пролетела
бы всего
l=3.108(м/с) .2.10-6 с=600 м
Однако частицы долетают до поверхности Земли, то есть преодолевают путь
10 км.
Движущаяся частица живёт дольше (с точки зрения наблюдателя на Земле).
Собственное время жизни частицы (в системе, с нею связанной) равно τ0,
но с «точки зрения частицы» сокращается её путь: длина движущейся
относительно частицы толщи атмосферы сокращается в направлении
движения.

16.

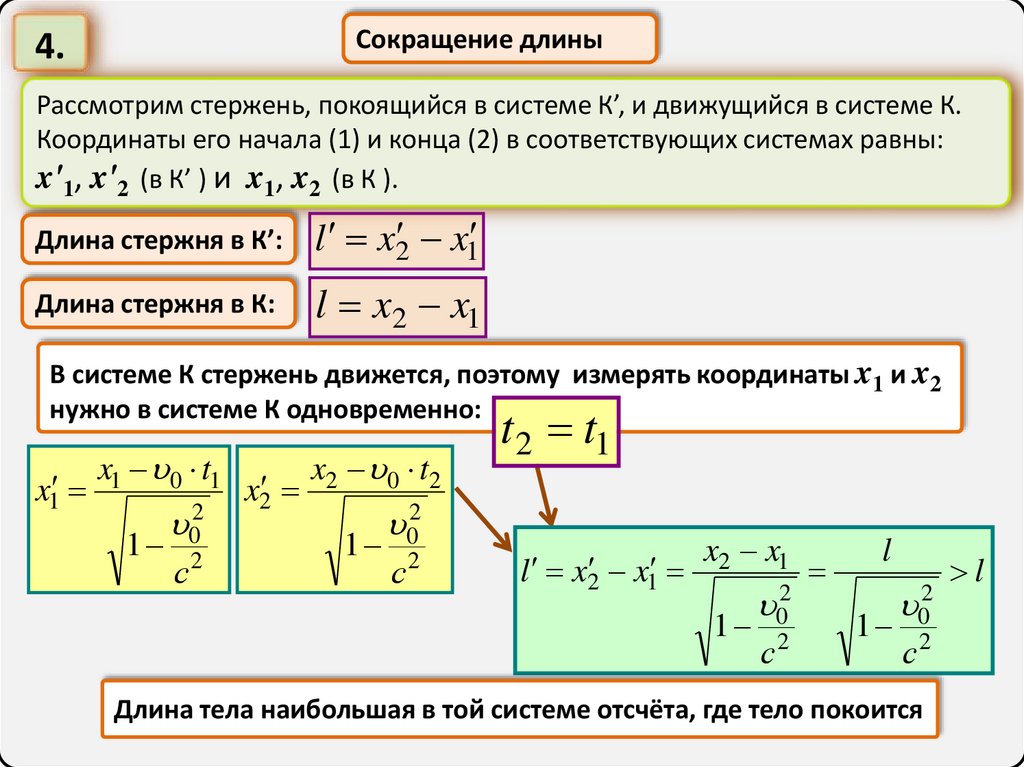
Сокращение длины
4.
Рассмотрим стержень, покоящийся в системе К’, и движущийся в системе К.
Координаты его начала (1) и конца (2) в соответствующих системах равны:
x'1, x'2 (в К’ ) и x1, x2 (в К ).
Длина стержня в К’:
l x2 x1
Длина стержня в К:
l x2 x1
В системе К стержень движется, поэтому
измерять координаты x1 и x2
ь
нужно в системе К одновременно:
x t
x t
x1 1 0 1 x2 2 0 2
1
02
с
2
1
02
с
2
t2 t1
l x2 x1
x2 x1
02
1 2
с
l
02
1 2
с
Длина тела наибольшая в той системе отсчёта, где тело покоится
l

17.

Интервал
Пространство и время в СТО образуют единую сущность –
пространство-время, описываемую четырьмя координатами (x,y,z,t)
Не сохраняется длина тел и продолжительность события,
но сохраняется интервал S между событиями
По определению, интервал S – это:
ь
S c t2 t1 x2 x1 y2 y1 z2 z1
2
2
2
2
2
Интервал между событиями – инвариант СТО:
2
2
2
2
2
S S c t2 t1 x2 x1 y2 y1 z2 z1

18.

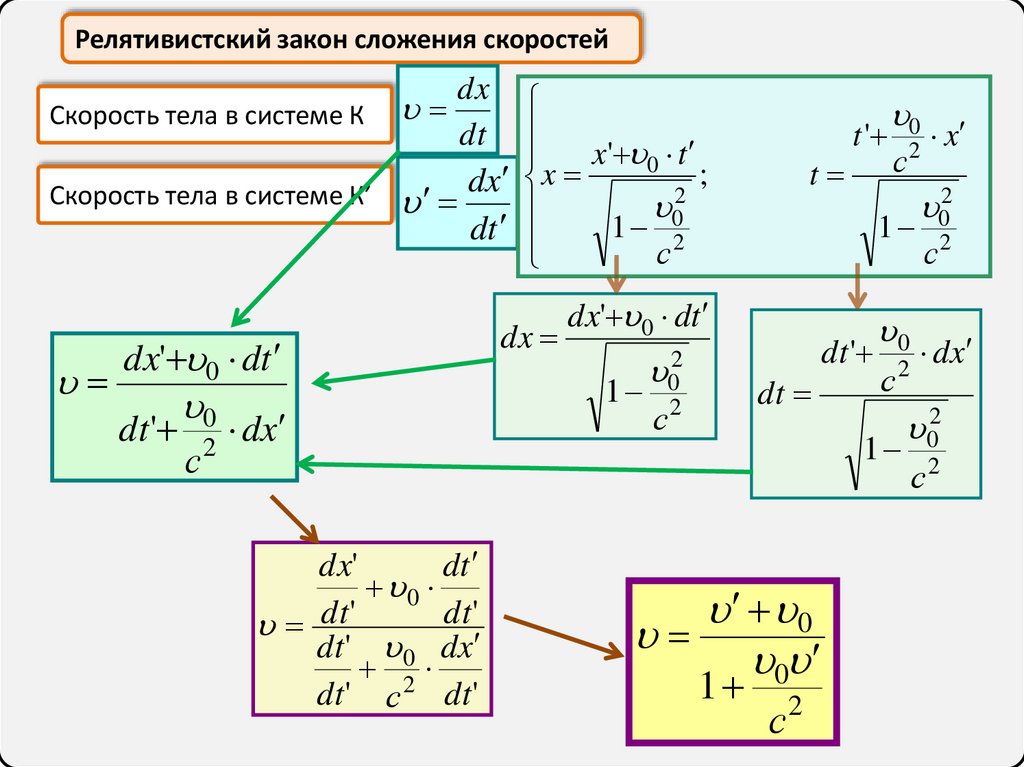
Релятивистский закон сложения скоростей
dx
Скорость тела в системе К
dt
x' 0 t
x
;
d
x
2
Скорость тела в системе К’
0
1
dt
с2
dx' 0 dt
dt'
0
с
dx
2
dx'
dt
0
dt'
dt'
dt ' 0 dx
2
dt ' с dt'
dx
t ' 20 x
с
t
dx' 0 dt
02
1 2
dt '
dt
с
1
02
0
dx
с
2
1
0
0
1
с2
с2
02
с2

19.

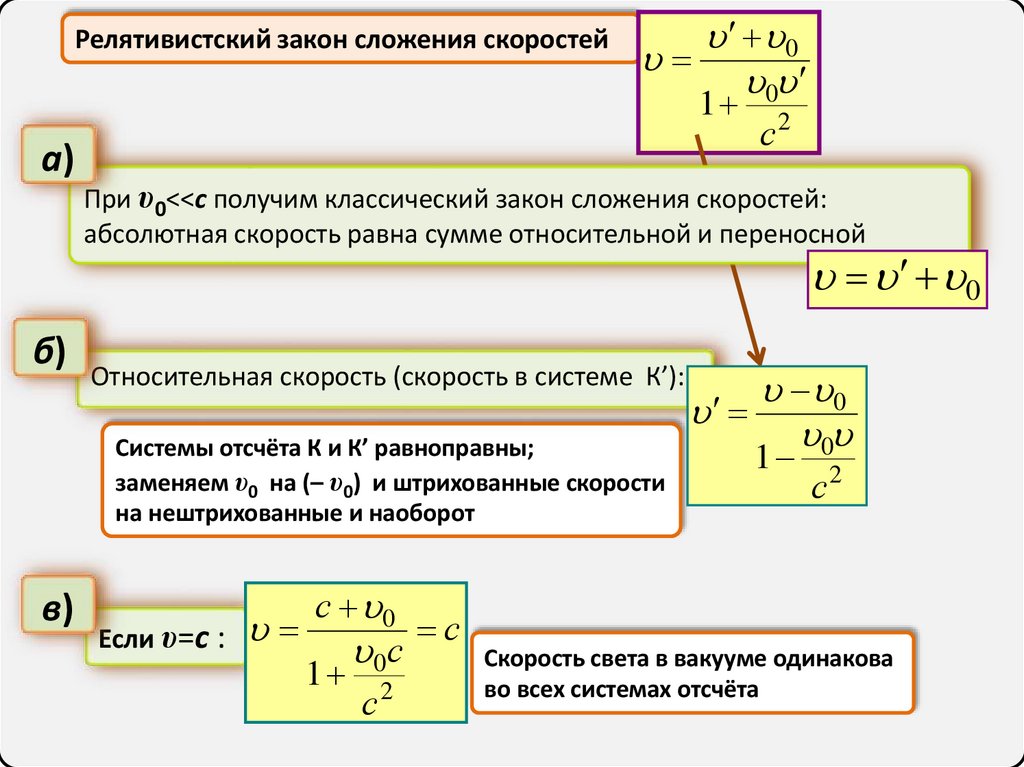
Релятивистский закон сложения скоростей
0
0
1
а)
с2
При υ0<<c получим классический закон сложения скоростей:
абсолютная скорость равна сумме относительной и переносной
0
б)
Относительная скорость (скорость в системе К’):
Системы отсчёта К и К’ равноправны;
заменяем υ0 на (– υ0) и штрихованные скорости
на нештрихованные и наоборот
в)
0
0
1
с2
с 0
с
Если υ=с :
0с
Скорость света в вакууме одинакова
1 2
во всех системах отсчёта
с

20.

Динамика СТО
Второй закон Ньютона
Импульс
по определению
Полная энергия;
взаимосвязь импульса
и полной энергии
Энергия покоя
Релятивистская масса
Верно
dp
F
dt
F ma
E
p 2
c
E E0 E кин.
E 2 p 2c 2 m 2c 4
E0 mc
Неверно
2
Не бывает
Масса покоя
Не бывает
Масса
m
p m
E mc 2
E m0c 2
E0 m0c 2
m0
m
1
m0
2
c2

21.

1.
Понятия «масса покоя» и «релятивистская масса» – не нужны
Если верна формула E=mс2 , то есть масса и энергия ПОЛНОСТЬЮ
эквивалентны, то зачем вводить ДВЕ разных величины, они же всё равно
связаны постоянной константой с2.
На самом деле масса и энергия – это разные понятия: любой массе
отвечает энергия (энергия покоя),
но не наоборот: не любой энергии отвечает масса
Формула E=mс2 вредна: она создаёт иллюзию, будто величина m
E
c2
является универсальной мерой инертности, а также универсальной
гравитационной массой.
В действительности для релятивистского тела понятие «гравитационной
массы» неприемлемо;
она зависит от направления скорости частицы в гравитационном поле

22.

Понятия «масса покоя» и «релятивистская масса» – не нужны
2.
Обычно объясняют невозможность достижения скорости света тем, что с
увеличением скорости растёт масса в соответствии с
m
m0
1
2
c2
,
поэтому при действии на тело постоянной силы требуется бесконечное
время для достижения скорости света.
Рассчитаем время, необходимое для разгона тела с «массой покоя» m0 от
нулевой начальной скорости до скорости света, если на него действует
постоянная сила F

23.

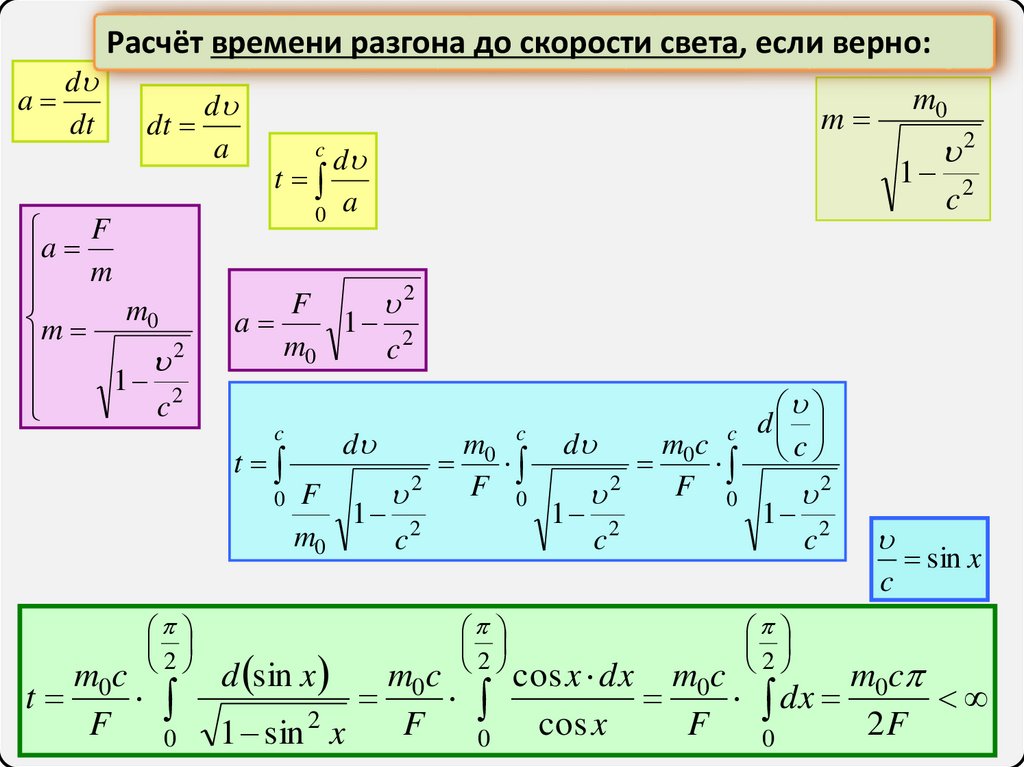
a
d
dt
Расчёт времени разгона до скорости света, если верно:
d
dt
a
F
a
m
m m0
2
1 2
c
m0
m
d
0 a
c
1
t
c
d
0
F
1 2
m0
c
m0 c
2
F 0
d
m0c c c
d
2
F 0
2
1 2
1 2
c
c
c
m0c
t
F
0
c2
F
2
a
1 2
m0
c
t
2
2
d sin x
2
2
sin x
m0c
m0c
cos x dx m0c
dx
2
F
cos x
F
2F
1 sin x
0
0

24.

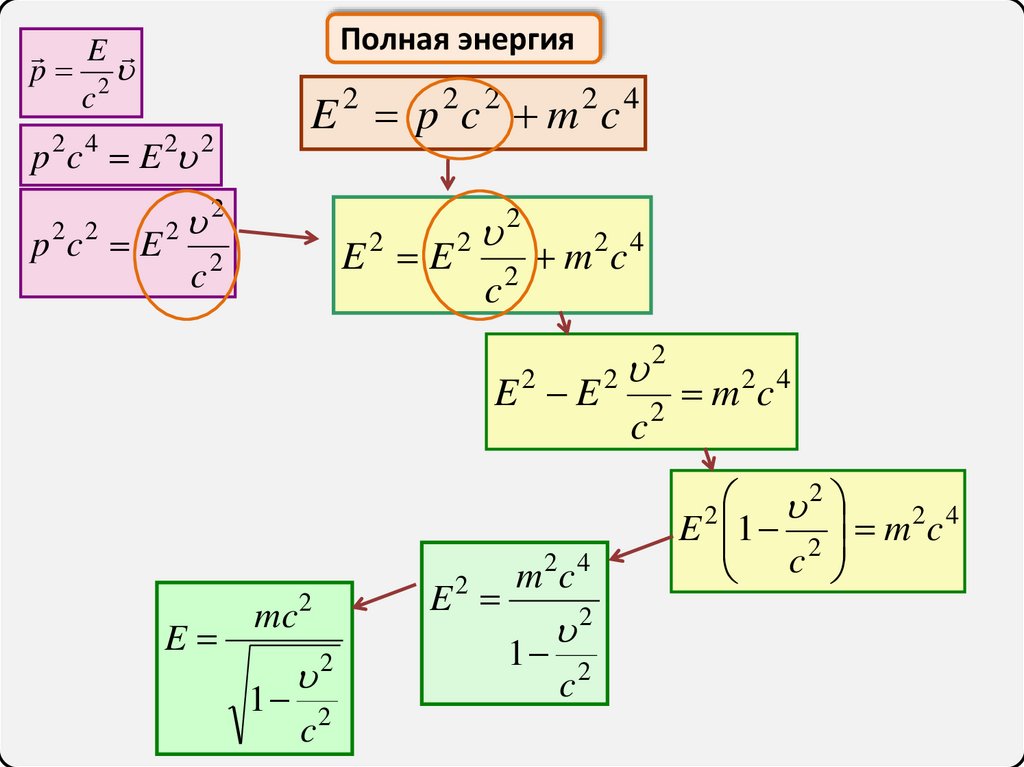
Полная энергия
E
p 2
c
E 2 p 2c 2 m 2c 4
p 2c 4 E 2 2
p c E
2 2
2
2
c
E2 E
2
2
2
c
2 4
m
c
2
E E
2
E
mc
1
E2
2
2
c2
m 2c 4
1
2
c2
2
c
2
2 4
m
c
2
2
E 2 1 2 m 2c 4
c

25.

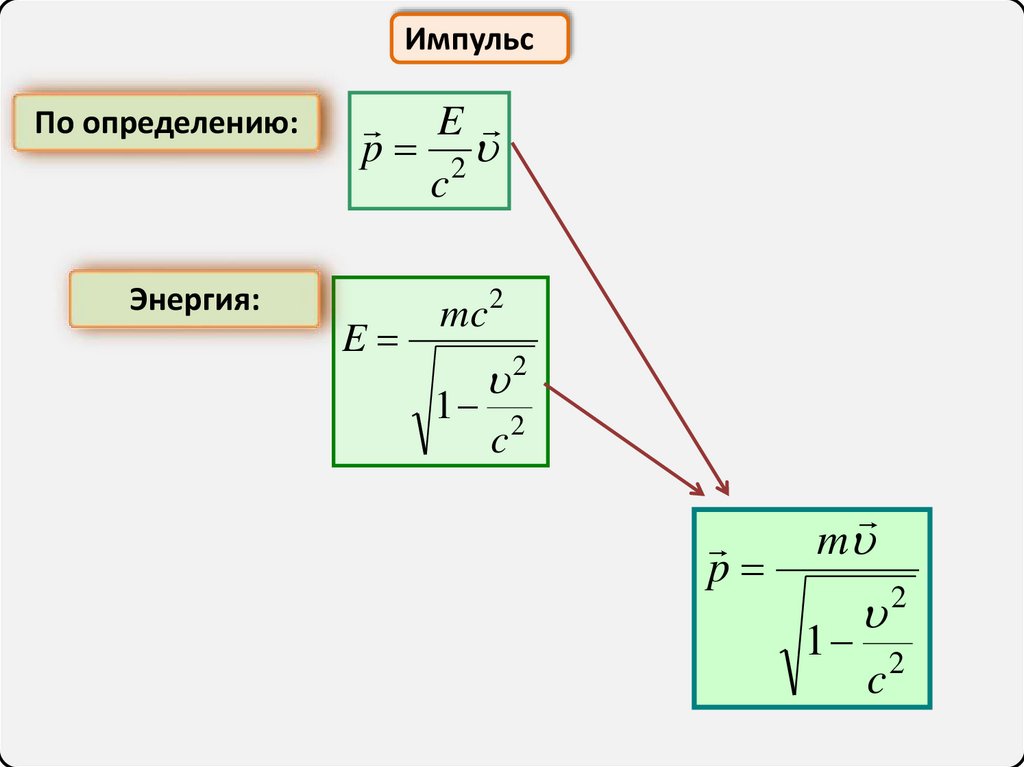
Импульс
По определению:
Энергия:
E
p 2
c
E
mc2
1
2
c2
p
m
1
2
c2

26.

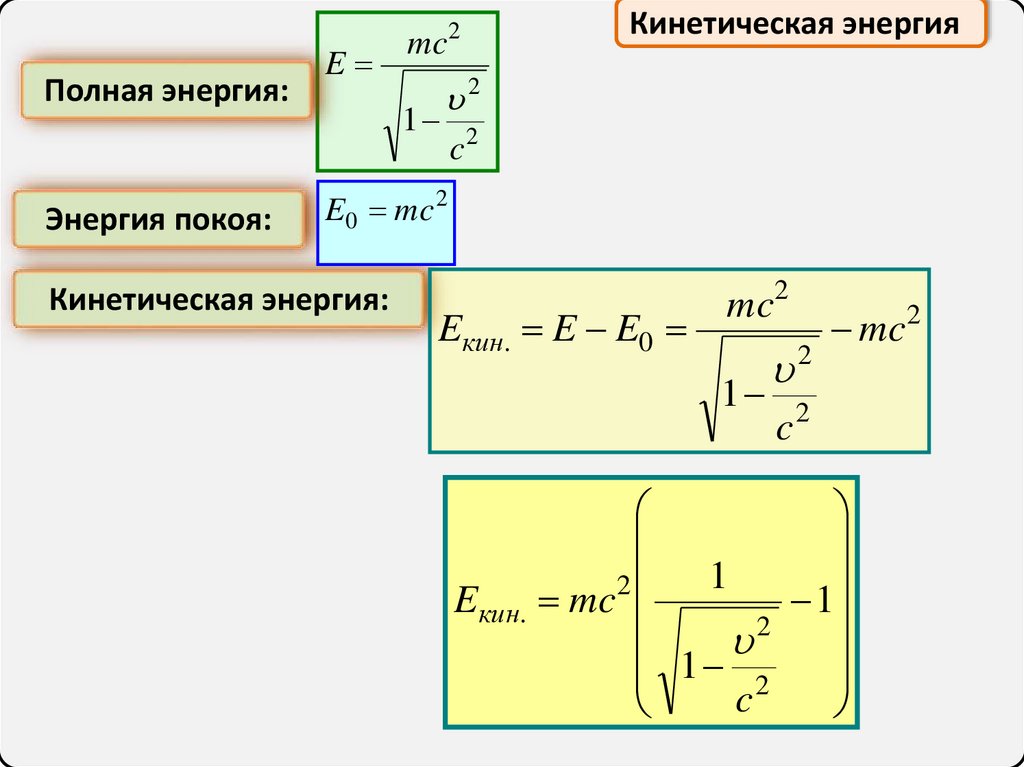
Полная энергия:
Энергия покоя:
E
mc2
1
Кинетическая энергия
2
c2
E0 mc 2
Кинетическая энергия:
Eкин. E E0
mc2
1
2
mc
c2
1
2
Eкин. mc
1
2
1
2
c
2

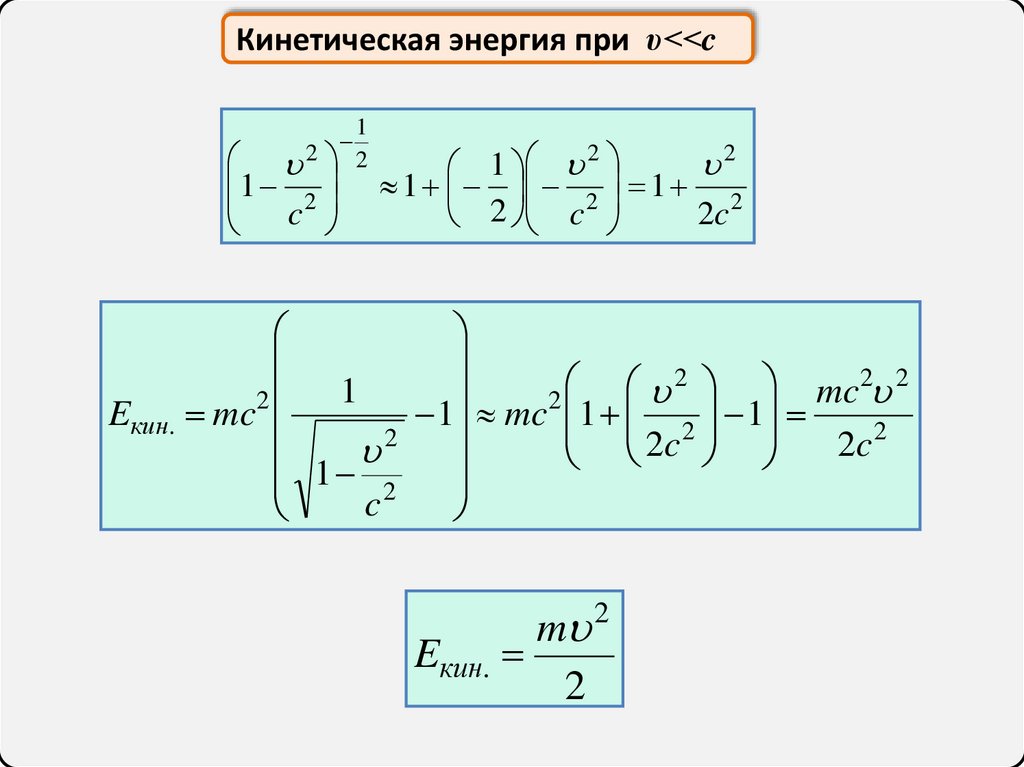
27.

Кинетическая энергия при υ<<c
1
2 2
1
c2
2
2
1
1 2 1 2
2c
2 c
2
2 2
1
mc
2
2
Eкин. mc
1 mc 1 2 1
2
2
2
c
2
c
1
2
c
m 2
Eкин.
2

28.

Энергия покоя – это:
внутренняя энергия частицы или тела,
не связанная с движением тела как целого
и его взаимодействием с внешними силовыми полями.
Для сложного тела его энергия покоя – это:
•суммарная энергия покоя всех его частиц;
•их кинетическая энергия движения относительно центра
масс тела и
•потенциальная энергия взаимодействия частиц между
собой.
При изменении энергии покоя меняется масса:
E0 mc 2
E0
m 2
с

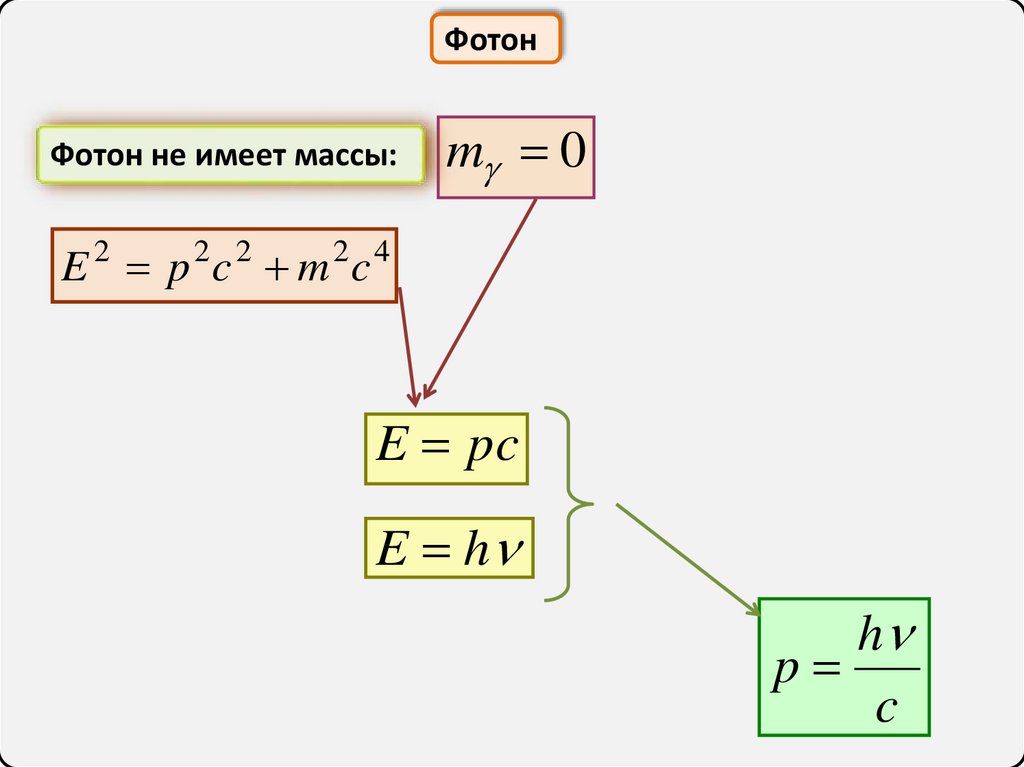
29.

Фотон
Фотон не имеет массы:
m 0
E 2 p 2c 2 m 2c 4
E pc
E h
h
p
c

30.

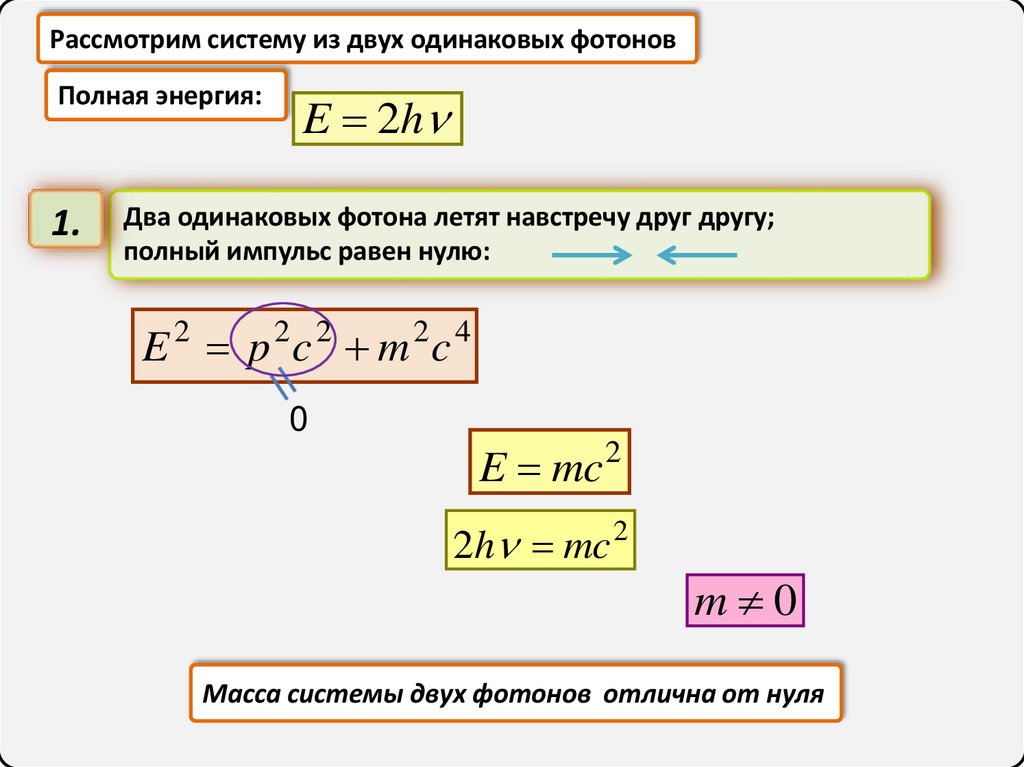
Рассмотрим систему из двух одинаковых фотонов
Полная энергия:
1.
E 2h
Два одинаковых фотона летят навстречу друг другу;
полный импульс равен нулю:
E 2 p 2c 2 m 2c 4
0
E mc 2
2h mc
2
m 0
Масса системы двух фотонов отлична от нуля

31.

Рассмотрим систему из двух одинаковых фотонов
Полная энергия:
2.
E 2h
Два одинаковых фотона летят в одну сторону;
модули импульсов складываются:
2 h
p
c
E 2 p 2c 2 m 2c 4
2h 2
2 4
2h
c
m
c
c
2
2
m 0
Масса системы двух фотонов равна нулю
Вывод: масса неаддитивна

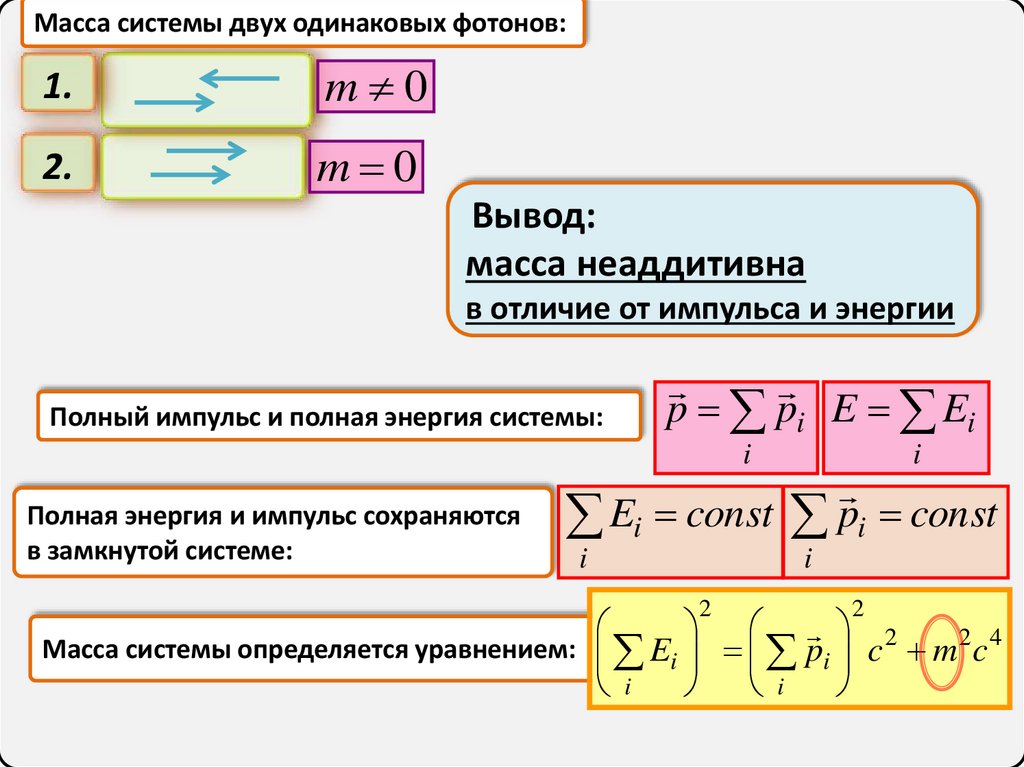
32.

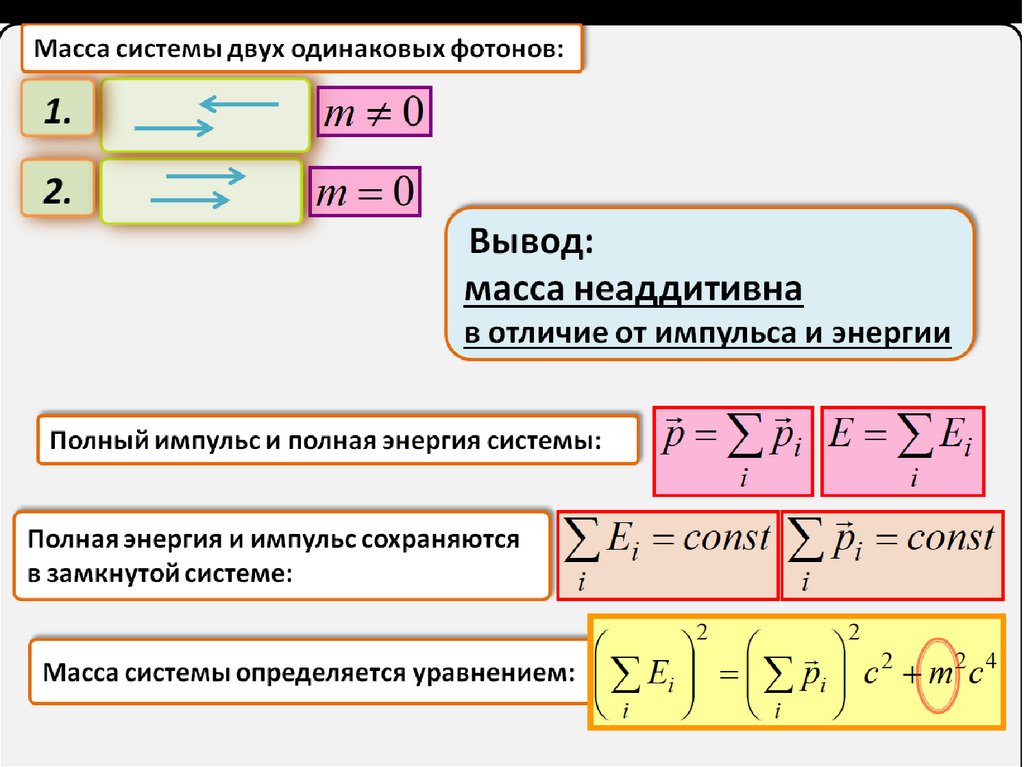
Масса системы двух одинаковых фотонов:
1.
m 0
2.
m 0
Вывод:
масса неаддитивна
в отличие от импульса и энергии
Полный импульс и полная энергия системы:
p pi E Ei
i
Полная энергия и импульс сохраняются
в замкнутой системе:
i
Ei const pi const
i
i
i
2
i
2
Масса системы определяется уравнением: Ei pi c 2 m 2 c 4

33.

33

34.

Масса - инвариант
Энергия и импульс меняются при переходе к другой
инерциальной системе отсчёта, но комбинация
E p c m c
2
2 2
2 4
(как и масса!) является лоренцевым инвариантом и не
меняется
Понятие «релятивистской массы» не используется и не рекомендуется к
применению, хотя оно и встречается в ранних работах по теории
относительности
Масса частицы m не зависит от скорости,
являясь инвариантом относительно преобразований Лоренца

35.

m
p
2
1 2
c
dp F
dt
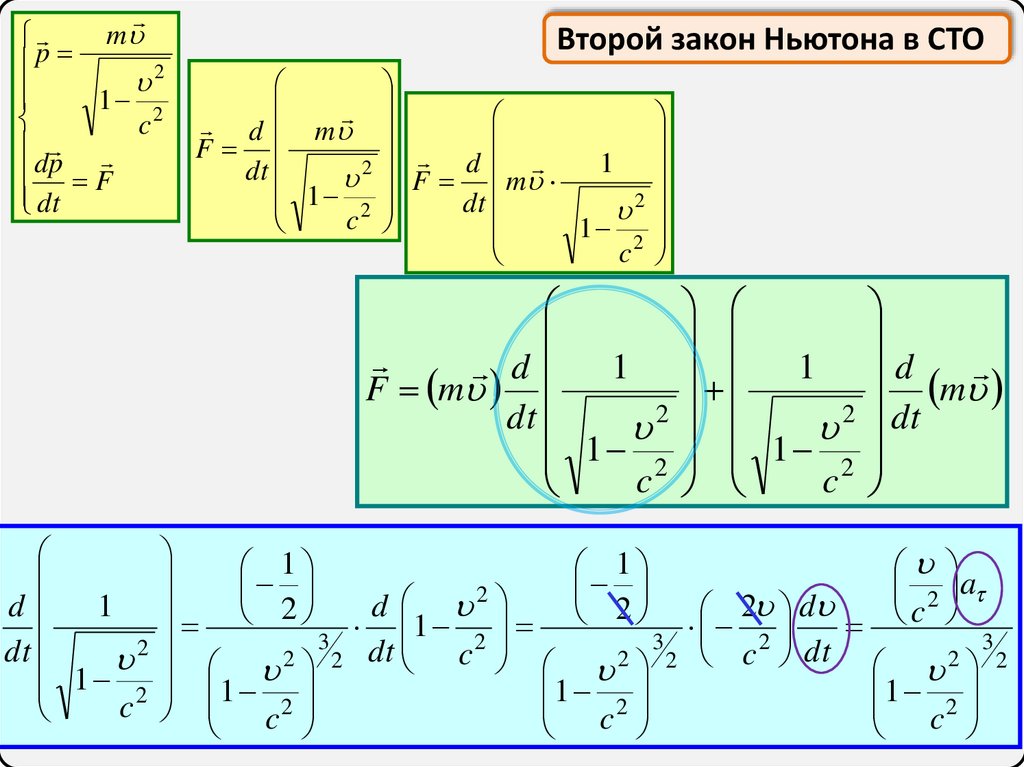
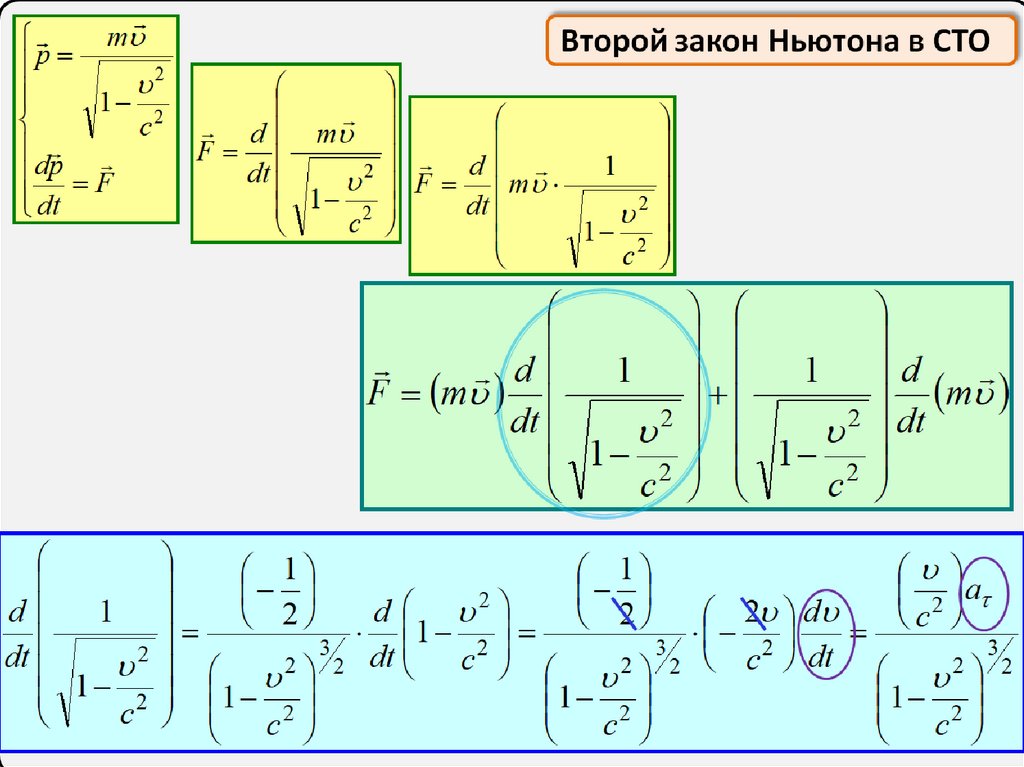
Второй закон Ньютона в СТО
d m
F
d
1
2
dt
F
m
1
2
dt
2
c
1
c2
d 1 1 d
F m
m
dt
2
2 dt
1 2 1 2
c
c
1
1
2 a
2
d 1
2 d 1 2 2 d c
2
3
2
3
3
2
dt
dt
dt
c
c
2
2
2
2
2
2
1
1
1
2 1 2
2
c2
c
c
c

36.

36

37.

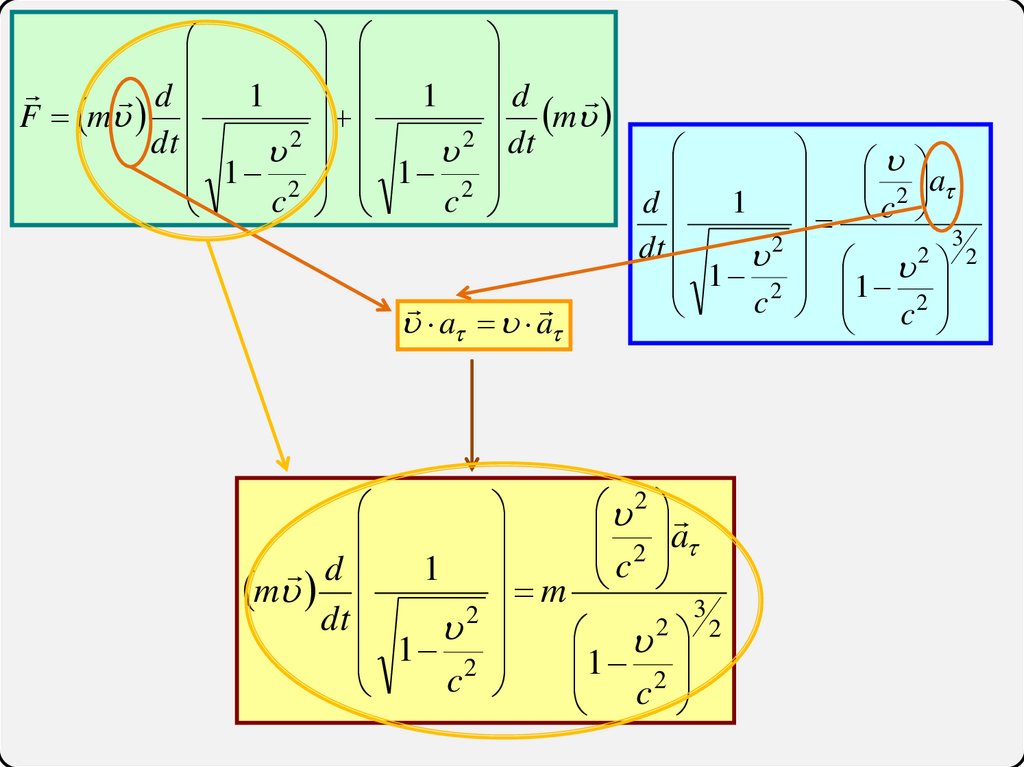
d 1 1 d
F m
m
dt
2
2 dt
1
1
2 a
2
2
c
c
d 1
c
3
2
dt
2
1
2
2 1 2
c c
a a
2
a
c2
d 1
m
m
3
2
dt
2
2
1
1
2
c2
c

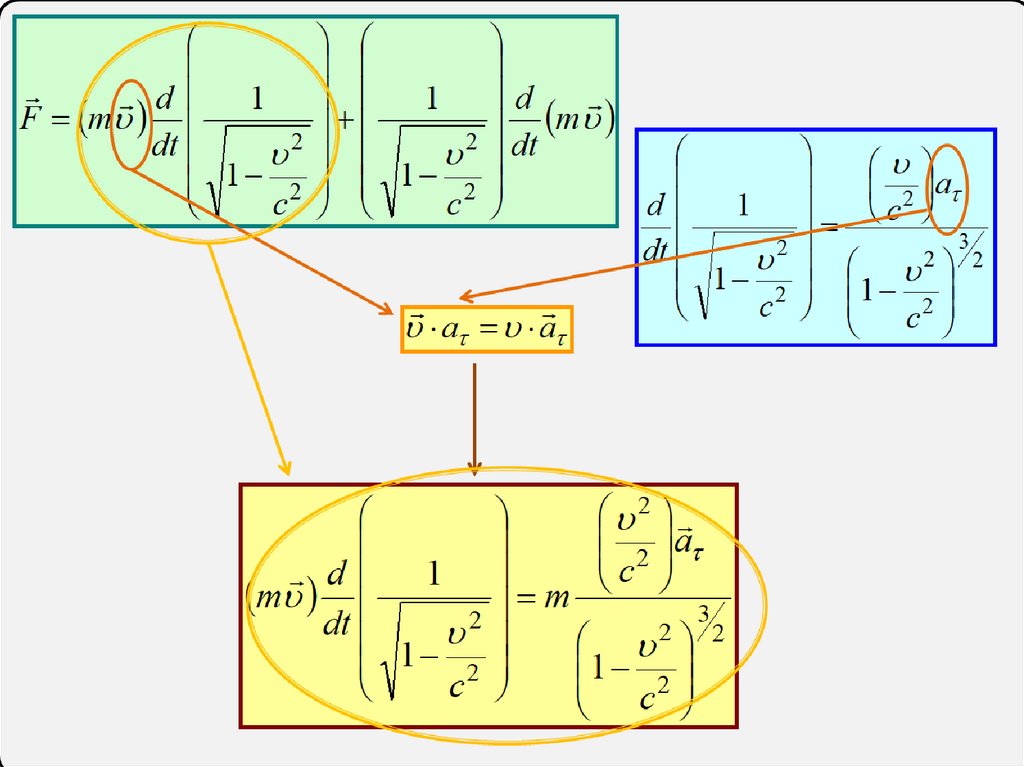
38.

38

39.

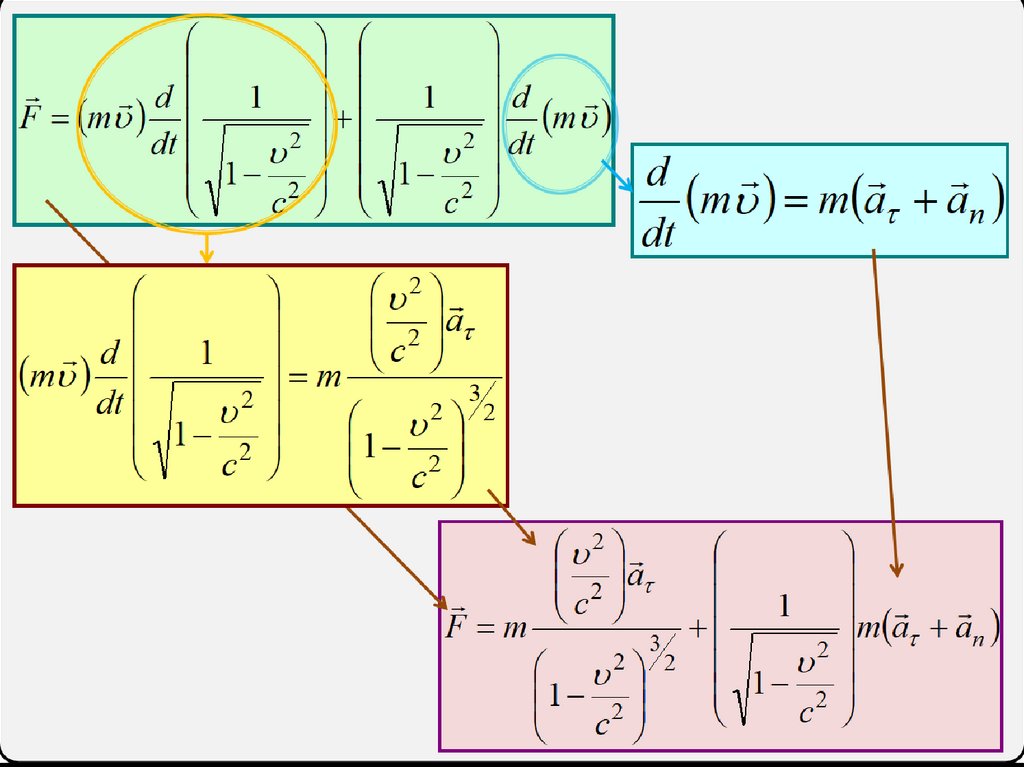
d 1 1 d
F m
m
dt
2
2 dt
1 2 1 2
c
c
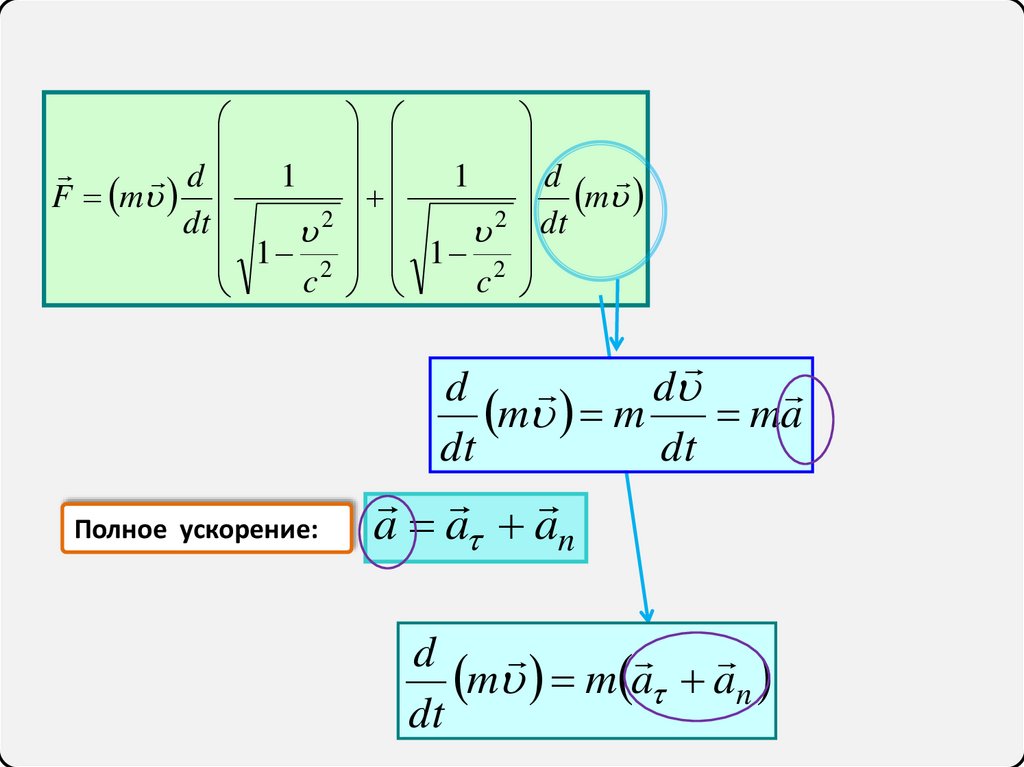
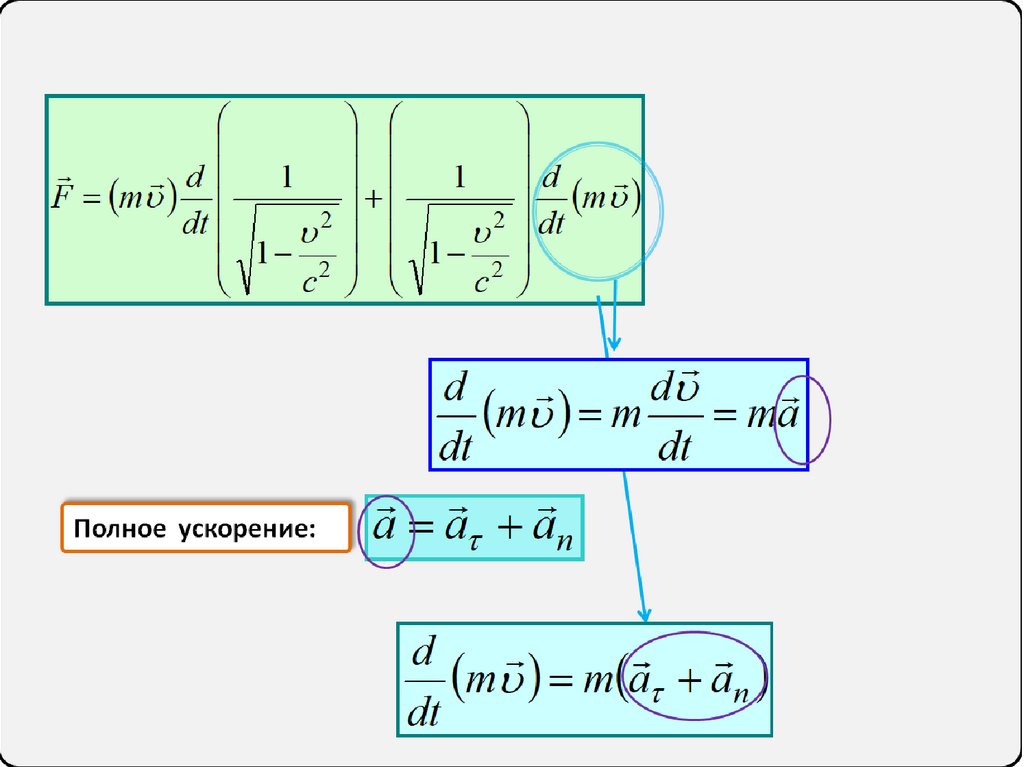
d
d
m m ma
dt
dt
Полное ускорение:
a a an
d
m m a an
dt

40.

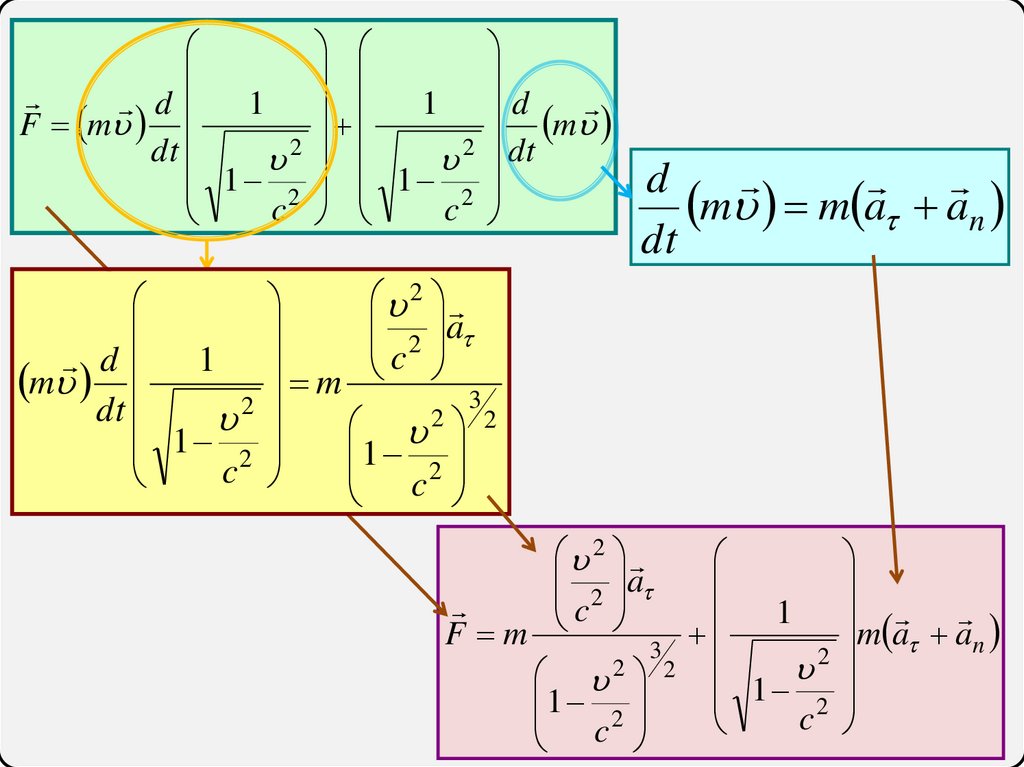
40

41.

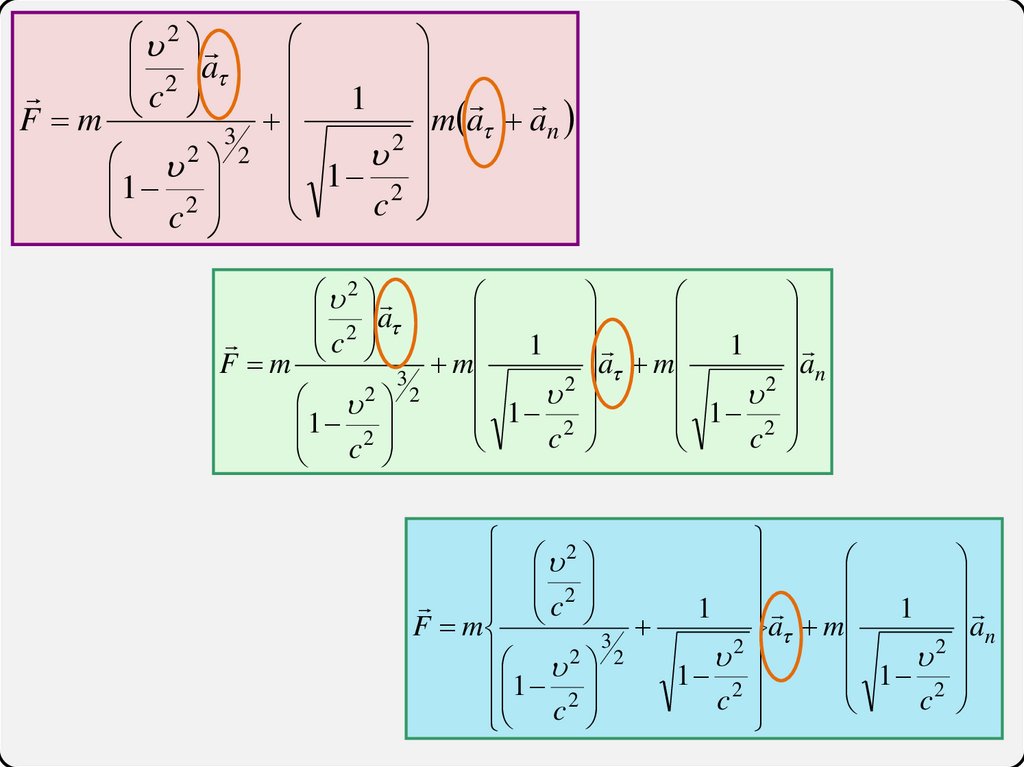
d 1 1 d
F m
m
dt
2
2 dt
1 2 1 2
c
c
d
m m a an
dt
2
a
c2
d 1
m
m
3
2
dt
2 2
1
1
2
c2
c
2
a
2
c
1
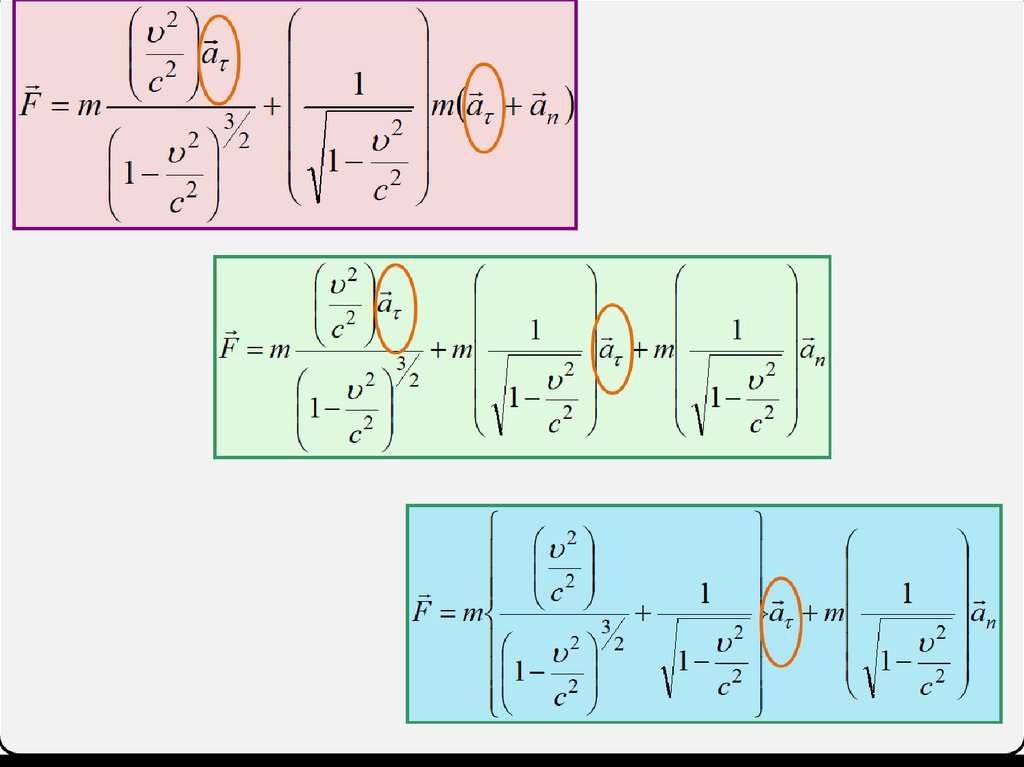
F m
m a an
3
2
2 2 1
1
2
c2
c

42.

42

43.

2
a
2
c
1
F m
m a an
3
2
2 2 1
1
2
c2
c
2
a
2
c
1
1
F m 3 m
a
m
an
2
2
2 2
1
1
1
2
2
c2
c
c
2
2
c
1
1
F m 3
a
m
an
2
2
2 2
1 2
1 2
1 2
c
c
c

44.

44

45.

2
2
1
1
c
F m
a
m
an
3
2
2
2 2
1
1
2
2
1 2
c
c
c
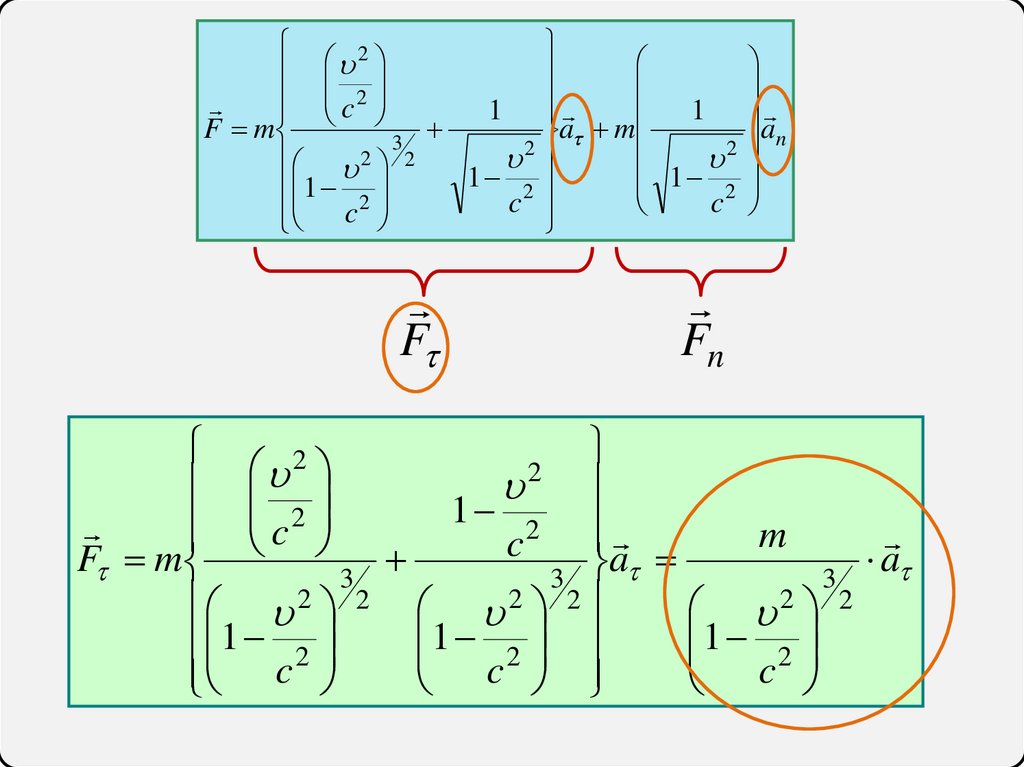
F
Fn
2
2
1 2
c 2
m
c
F m
a
a
3
3
3
2 2 2 2
2 2
1
1
1 2
2
2
c
c
c

46.

46

47.

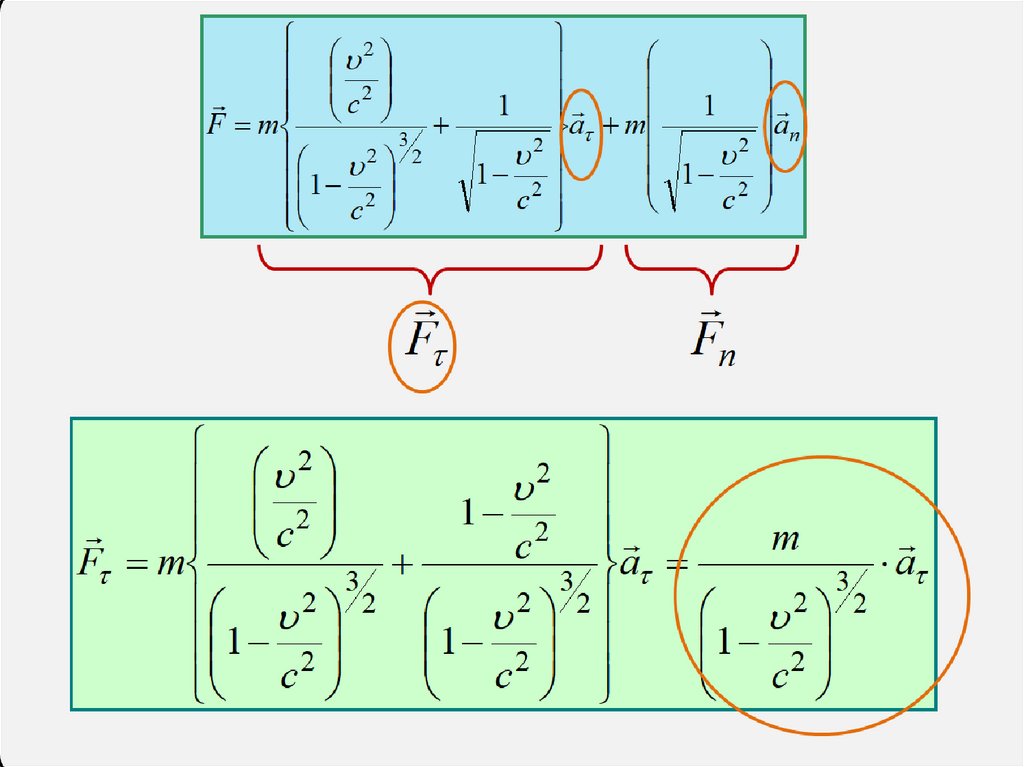
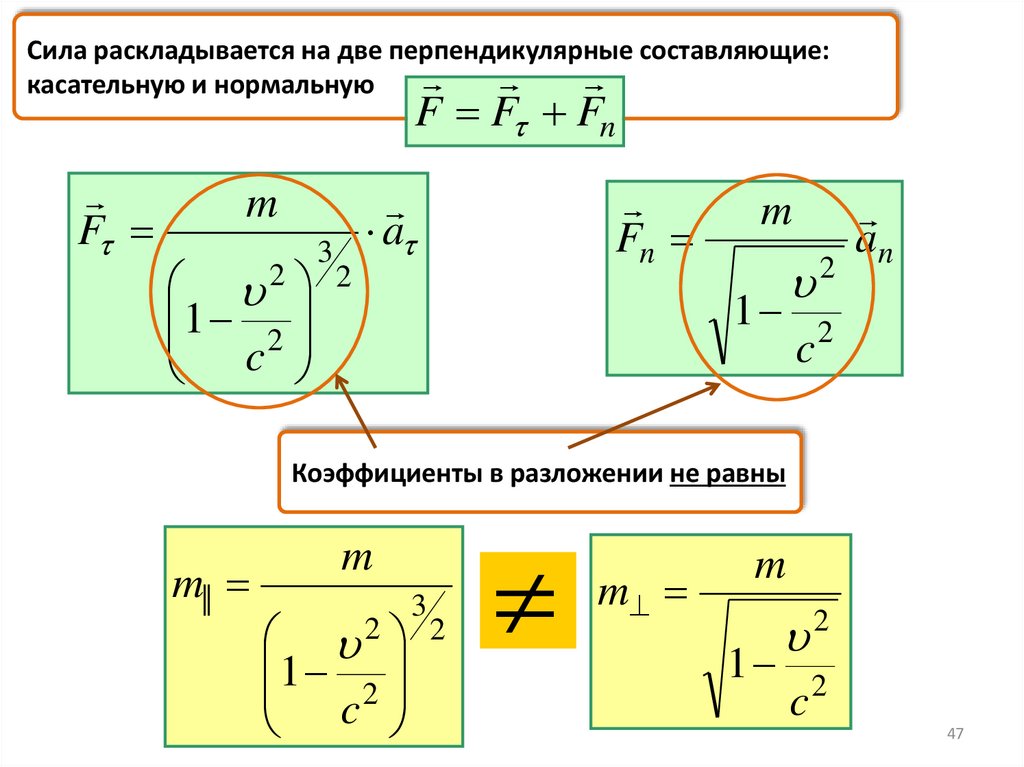
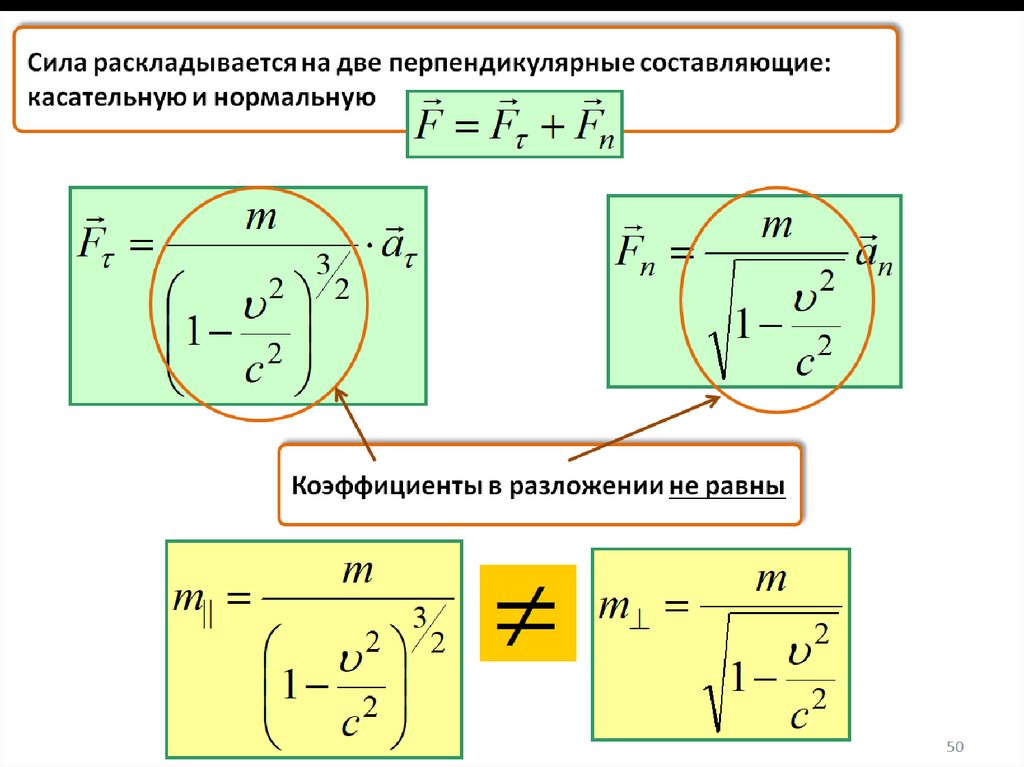
Сила раскладывается на две перпендикулярные составляющие:
касательную и нормальную
F F Fn
F
m
1
c2
3
2 2
Fn
a
m
1
2
an
c2
Коэффициенты в разложении не равны
m||
m
1
c2
3
2 2
m
m
1
2
c2
47

48.

48

49.

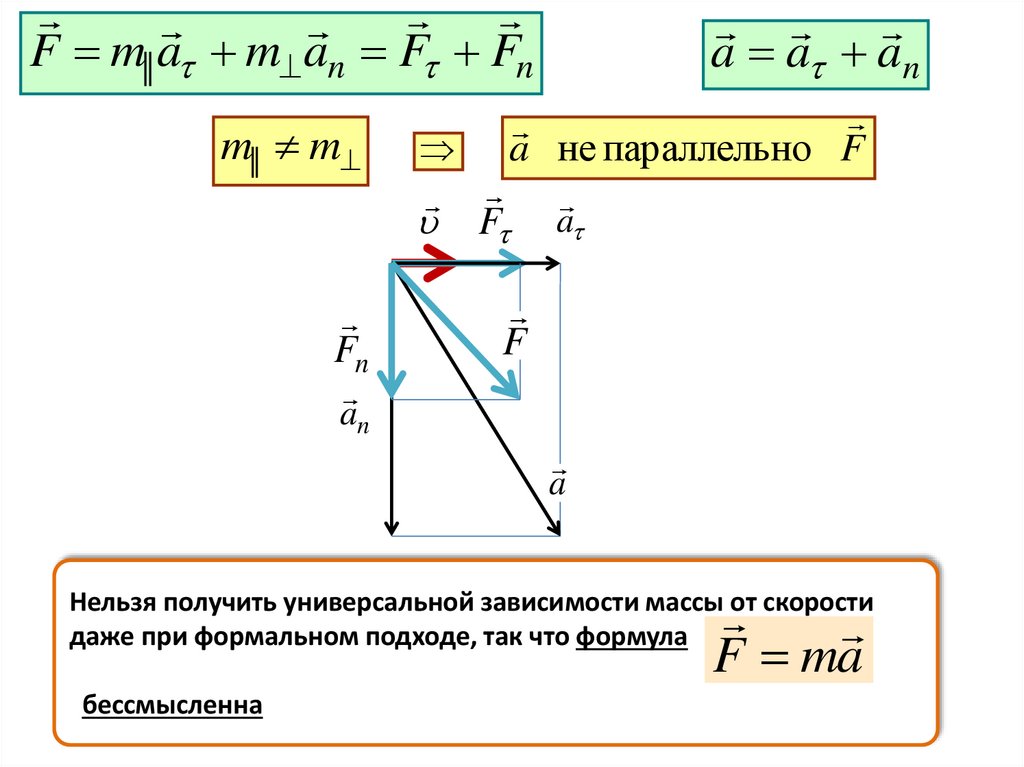
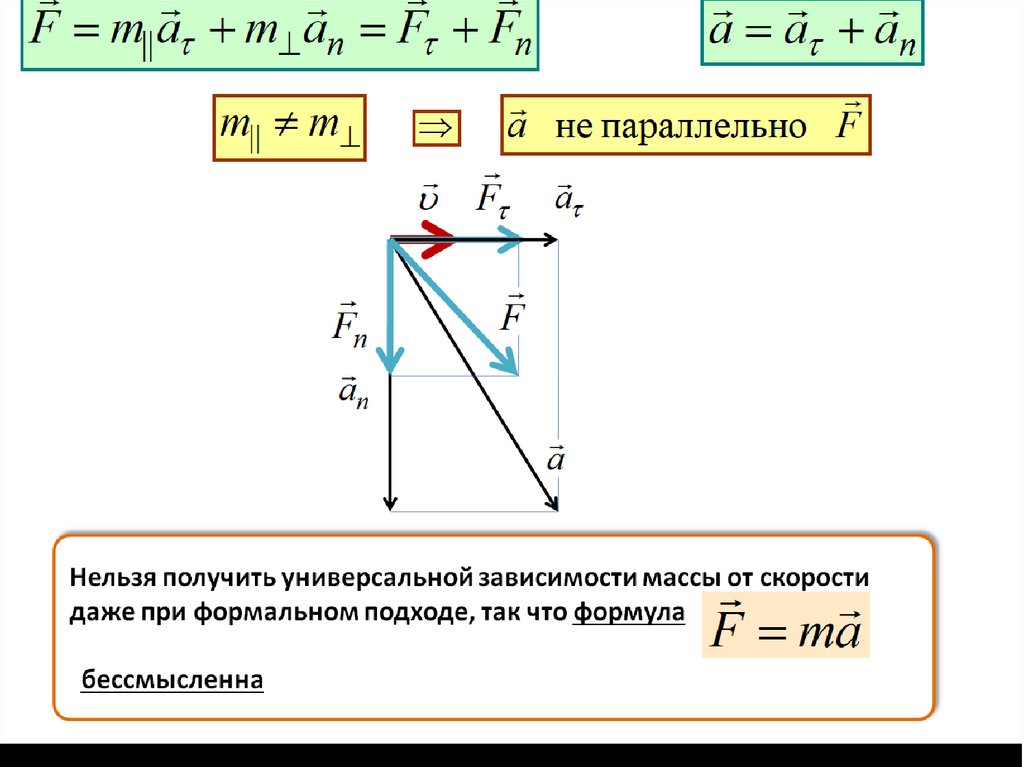
F m|| a m an F Fn
m|| m
Fn
a a an
a не параллельно F
F
a
F
an
a
F ma
Нельзя получить универсальной зависимости массы от скорости
даже при формальном подходе, так что формула
бессмысленна

50.

50

51.

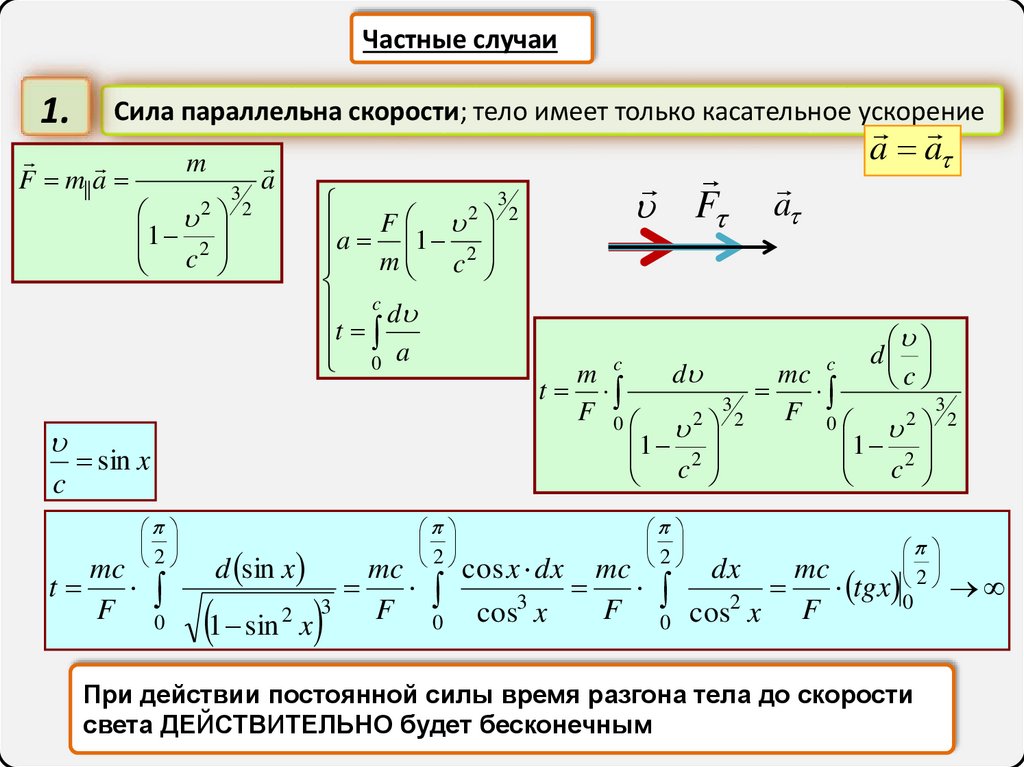
Частные случаи
1.
Сила параллельна скорости; тело имеет только касательное ускорение
F m|| a
c
m
1
c2
3
a
3
2
2
F
a 1
m c 2
c d
t
0 a
2 2
sin x
t
2
mc
F 0
d sin x
1 sin x
2
3
2
F
a
a a
d
c
m c
d
mc c
t
3
3
F 0
F
2 2
2
0
2
1
1
c2
c2
2
mc
cos x dx mc
dx
F 0 cos3 x
F 0 cos2 x
mc
tgx 0 2
F
При действии постоянной силы время разгона тела до скорости
света ДЕЙСТВИТЕЛЬНО будет бесконечным

52.

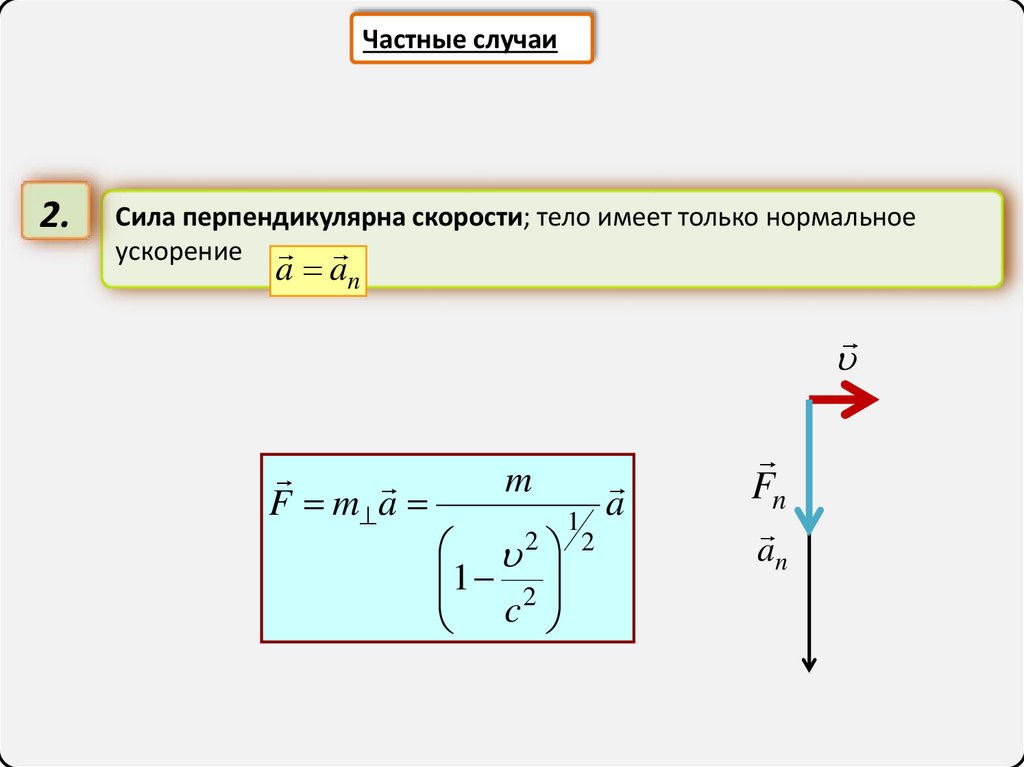
Частные случаи
2.
Сила перпендикулярна скорости; тело имеет только нормальное
ускорение
a an
F m a
m
1
c2
a
1
2 2
Fn
an

53.

Выводы
Многие предсказания теории относительности противоречат интуиции,
кажутся невероятными и невозможными.
Это не означает, что теория относительности неверна.
Ни одна из попыток опровергнуть СТО не смогла найти ни малейшего
изъяна в теории.
Теория верна математически: строгая математическая форма и чёткость
всех формулировок.
Новая теория является расширением старой и лишь ограничивает область
применения старой теории, не опровергая её.
На практике мы пользуемся теорией Ньютона, так как при скоростях, много
меньших скорости света, её предсказания очень мало отличаются от
предсказаний теории относительности.
Теория Ньютона имеет и то преимущество, что с ней гораздо проще
работать, чем с теорией Эйнштейна

54.

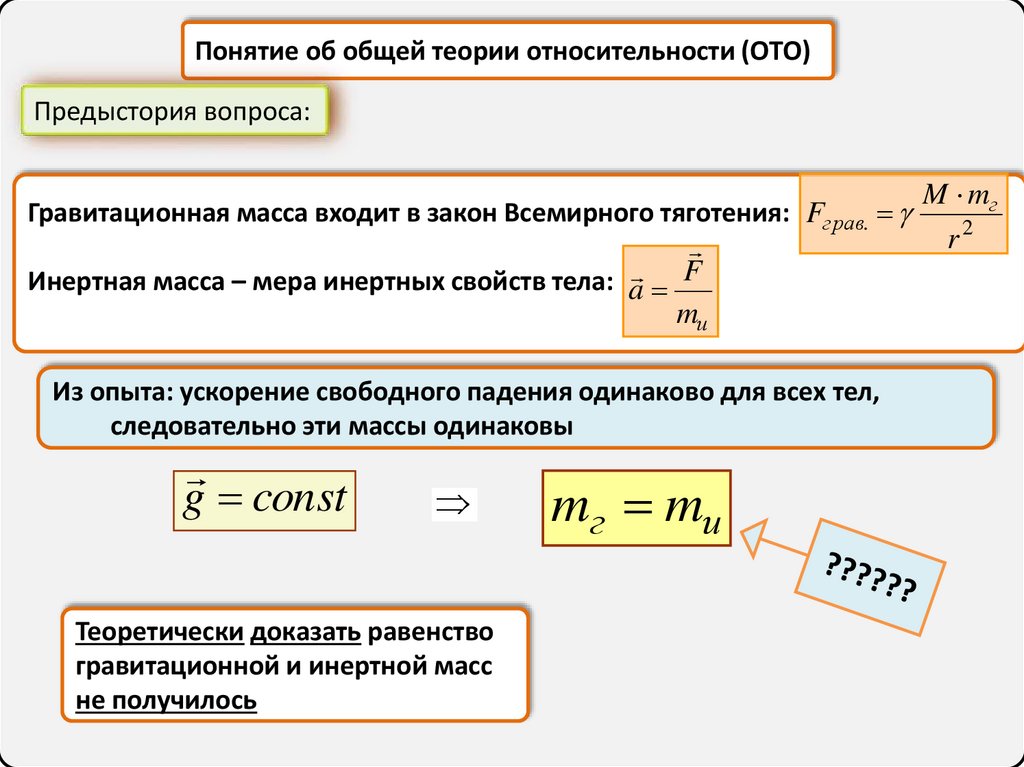
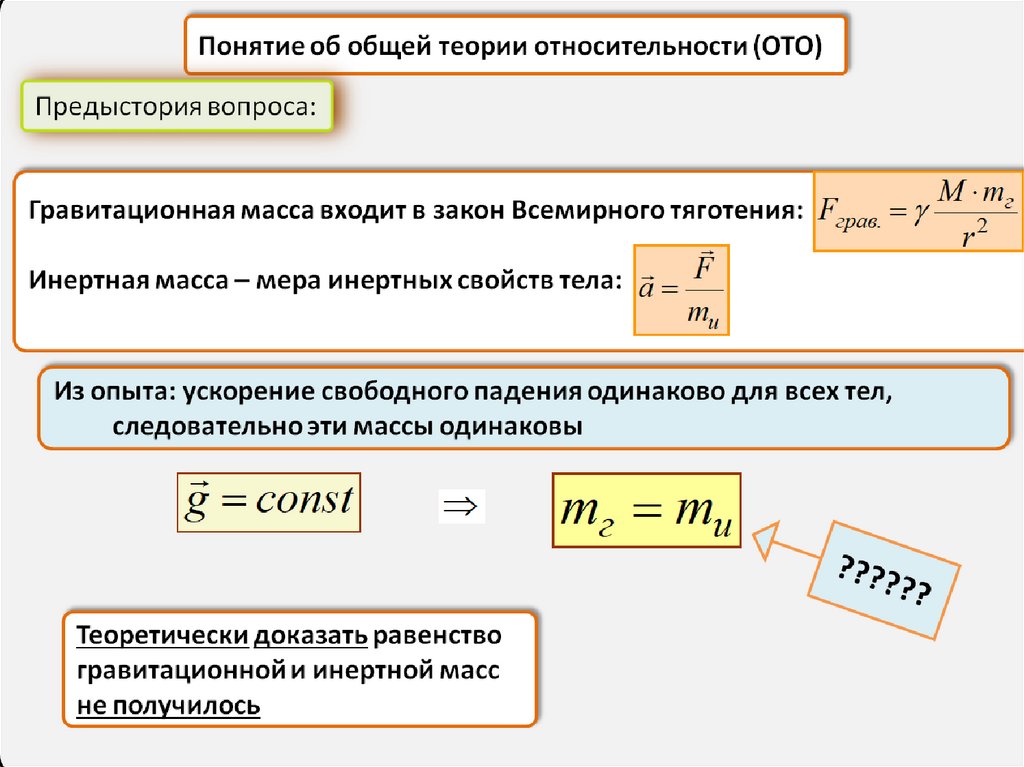
Понятие об общей теории относительности (ОТО)
Предыстория вопроса:
M mг
Гравитационная масса входит в закон Всемирного тяготения: Fграв.
r2
Инертная масса – мера инертных свойств тела: a F
mи
Из опыта: ускорение свободного падения одинаково для всех тел,
следовательно эти массы одинаковы
g const
Теоретически доказать равенство
гравитационной и инертной масс
не получилось
mг mи

55.

55

56.

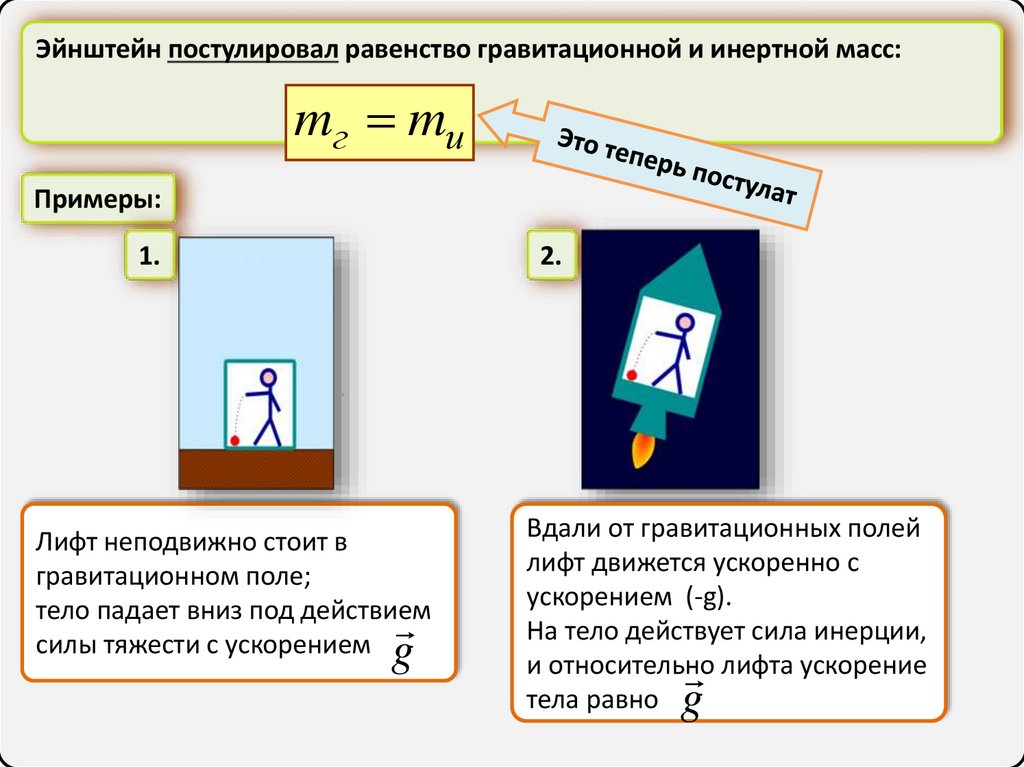
Эйнштейн постулировал равенство гравитационной и инертной масс:
mг mи
Примеры:
1.
2.
Лифт неподвижно стоит в
гравитационном поле;
тело падает вниз под действием
силы тяжести с ускорением
g
Вдали от гравитационных полей
лифт движется ускоренно с
ускорением (-g).
На тело действует сила инерции,
и относительно лифта ускорение
тела равно
g

57.

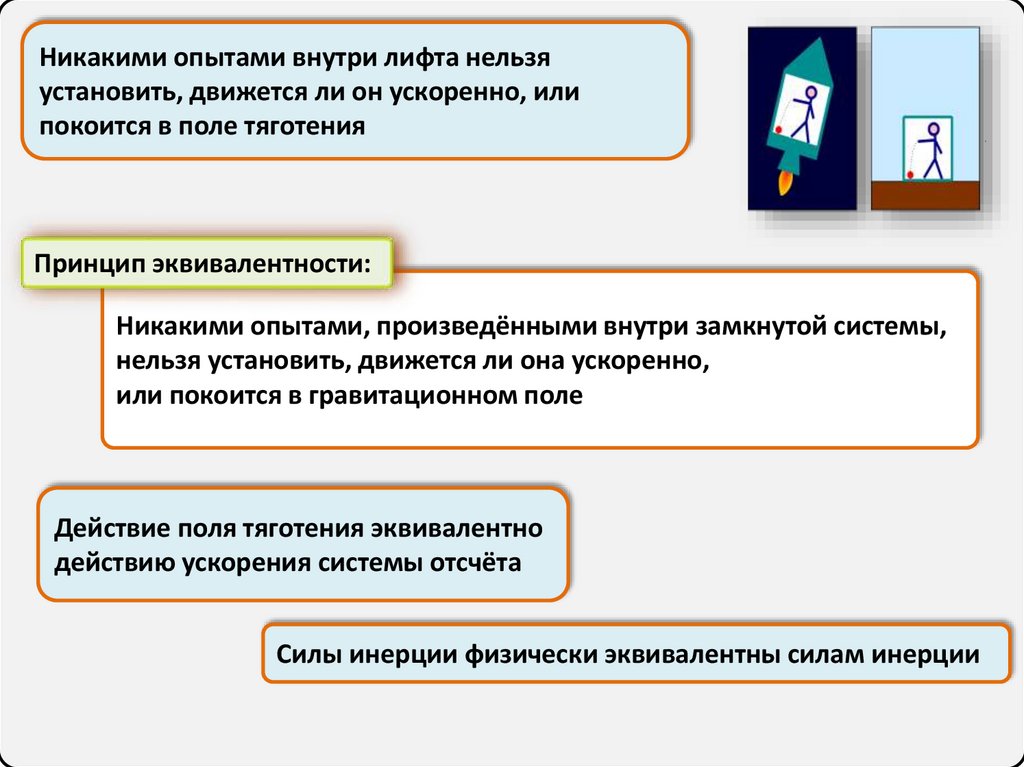
Никакими опытами внутри лифта нельзя
установить, движется ли он ускоренно, или
покоится в поле тяготения
Принцип эквивалентности:
Никакими опытами, произведёнными внутри замкнутой системы,
нельзя установить, движется ли она ускоренно,
или покоится в гравитационном поле
Действие поля тяготения эквивалентно
действию ускорения системы отсчёта
Силы инерции физически эквивалентны силам инерции

58.

Следствия:
Длительность событий и длина тел зависят от
гравитационного потенциала:
f ( )
l f ( )
Геометрия пространства-времени зависит от полей тяготения
Вблизи массивных тел:
время замедляется
длина тел сокращается в направлении вектора G напряжённости
гравитационного поля
Кажется, что луч света «притягивается»
к массивному телу
Само пространство искривлено; луч
идёт по пути, соответствующему
минимальному времени

59.

Экспериментальные доказательства:
1.
2.
2.
f ( )
Эффект замедления времени вблизи массивных тел:
в спектре излучения Солнца частота ниже, чем аналогичного
излучения тех же элементов, находящихся на Земле
Чем сильнее гравитация, тем медленнее протекает время.
Этот факт обязательно учитывается при работе GPS и ГЛОНАСС.
На спутниках часы тикают чуть-чуть быстрее, чем на Земле.
Если этот факт не учитывать, то уже через сутки погрешность
координат составит 10 км
f ( )
ОТО объяснила постепенное смещение перигелия орбиты Меркурия
(обнаружено в XIX веке).
Ньютоновская теория всемирного тяготения объяснить смещение не
смогла
Расчёт на основе общей теории относительности с замечательной
точностью совпал с наблюдениями

60.

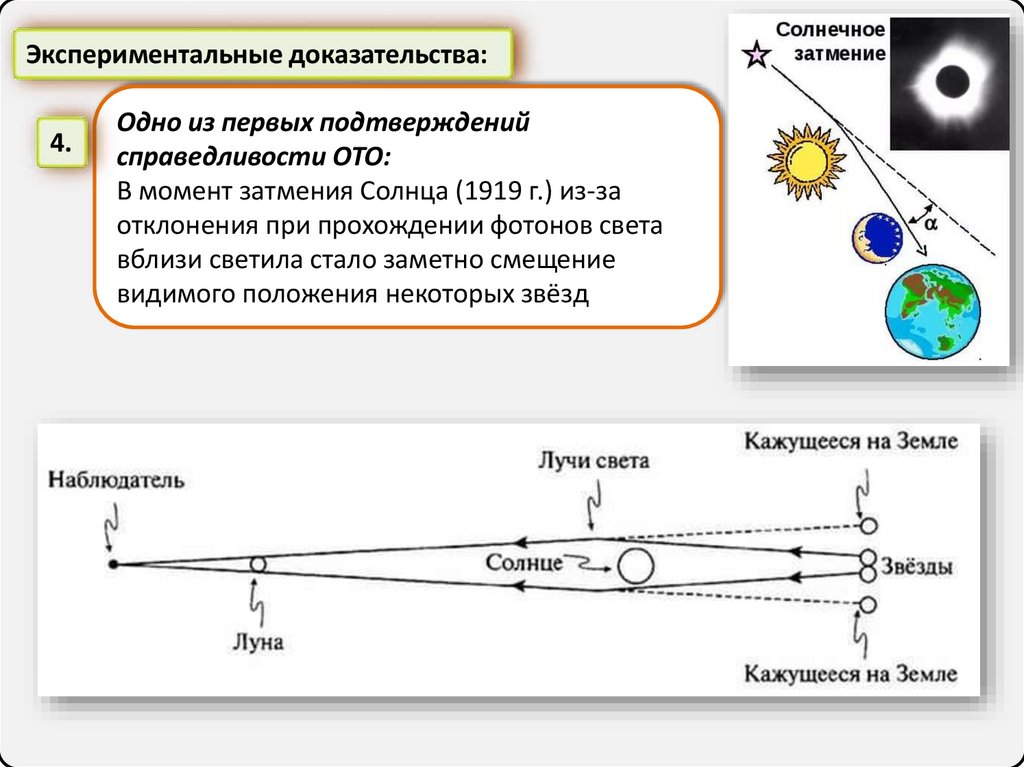
Экспериментальные доказательства:
4.
Одно из первых подтверждений
справедливости ОТО:
В момент затмения Солнца (1919 г.) из-за
отклонения при прохождении фотонов света
вблизи светила стало заметно смещение
видимого положения некоторых звёзд

61.

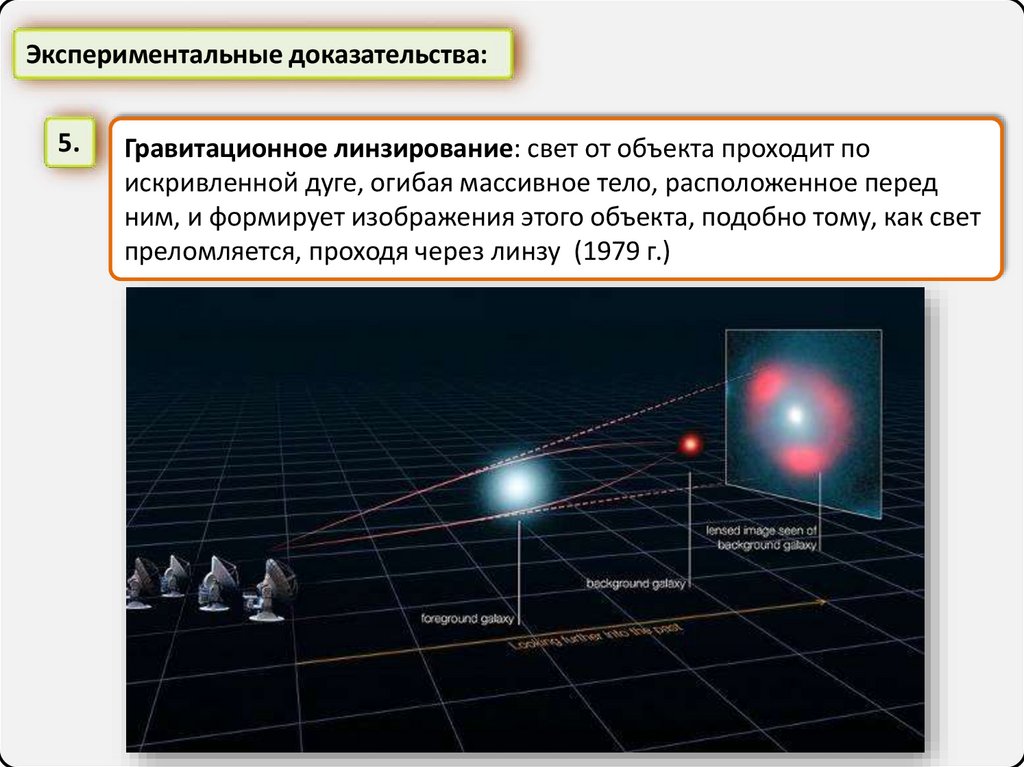
Экспериментальные доказательства:
5.
Гравитационное линзирование: свет от объекта проходит по
искривленной дуге, огибая массивное тело, расположенное перед
ним, и формирует изображения этого объекта, подобно тому, как свет
преломляется, проходя через линзу (1979 г.)

62.

Экспериментальные доказательства:
6.
Гравитационные волны, предсказанные ОТО, наконец обнаружены.
О первом прямом детектировании гравитационных волн
коллаборациями LIGO и VIRGO было объявлено 11 февраля 2016 года.
Гравитационные волны представляют собой рябь пространства,
распространяющуюся во времени со скоростью света: при
прохождении гравитационной волны между двумя свободно
падающими телами расстояние между ними изменяется
Астрофизики обнаружили место, где
предположительно находились две черные
дыры, слияние которых породило недавно
найденные гравитационные волны

63.

Экспериментальные доказательства:
7.
Существование чёрных дыр. Тяготение массивного объекта,
искривляя пространство, создает в пространстве «впадину», в
которую скатываются свет и материя. Чем плотнее объект, тем глубже
впадина. Черная дыра, самый плотный объект во Вселенной, создает
такую глубокую впадину, из которой ничто не может вырваться
наружу

64.

Заключение:
Нет ни одного надёжного экспериментального свидетельства,
опровергающего Общую Теорию Относительности