Лекция №4 Основные методы решения неравенств

1. 24.01. 26 Лекция №4 Различные методы решения неравенств

«МЕТОД РЕШЕНИЯ ХОРОШ,
ЕСЛИ С САМОГО НАЧАЛА
МЫ МОЖЕМ ПРЕДВИДЕТЬ –
И ВПОСЛЕДСТВИИ ПОДТВЕРДИТЬ,
ЧТО, СЛЕДУЯ ЭТОМУ МЕТОДУ,
МЫ ДОСТИГНЕМ ЦЕЛИ.»
ЛЕЙБНИЦ

2. Общие методы решения неравенств

1. Обобщенный метод интервалов.
2. Метод замены переменной.
3. «Расщепление» неравенств.
4. Метод рационализации.
5. Использование свойств функции.
5.1. Исследование области определения функции.
5.2. Использование свойства ограниченности
функции.
5.3. Использование свойства монотонности
функции.

3. 1. Обобщенный метод интервалов

Применимость метода интервалов не
ограничивается решением рациональных
неравенств.
Применяя метод интервалов к
решению иррациональных,
трансцендентных, комбинированных
неравенств, говорят об обобщенном
методе интервалов.

4. Алгоритм обобщенного метода интервалов

1) Привести неравенство к виду
>0.
2) Найти область определения функции
же ОДЗ переменной).
3) Найти нули функции
(она
, решив уравнение
4) Изобразить на числовой прямой область
определения и нули функции.
5) Определить знаки функции на промежутках,
входящих в область определения функции.
6) Записать ответ, включив в него промежутки в
соответствии со знаком неравенства (не забыть
включить в ответ изолированные точки).

5.

Методы
Метод интервалов.
Пример 1.
5
Метод интервалов – это универсальный способ решения
практически любых неравенств, которые встречаются в
школьном курсе алгебры.
Пример 1.
4 x x 5 0
4 x 0
ОДЗ :
x 5 0
Найдем нули функции
4 x x 5 0
4 x x 5
4 x x 5
1
x ОДЗ
2
5
x 4
x 5
x [ 5 ;4 ]
1
2
4
Определим знаки функции на полученных
промежутках и учтем ОДЗ.
1
Ответ : 5 ;
2
24.01.2026

6.

Методы
Метод интервалов.
Пример 2.
6
x 2 5 x 6 2 x 2 6 x 15
x 2 5 x 6 2 x 2 6 x 15 0
Найдем нули функции
x 2 5 x 6 2 x 2 6 x 15 0
x 2 5 x 6 2 x 2 6 x 15
x 2 5 x 6 2 x 2 6 x 15
x2 x 9 0
1 37 ОДЗ
x
2
1 37 ОДЗ
x
2
1 37
2
x2 5 x 6 0
ОДЗ : 2
2 x 6 x 15 0
( x 6 )( x 1 ) 0
3 39
3 39
x
0
x
2
2
3 39
2
3 39
2
1
3 39
2
6
6
Далее нужно определить знаки функции на
полученных промежутках.

7.

Методы
Метод интервалов.
Пример 2.
7
x 2 5 x 6 2 x 2 6 x 15
x 5 x 6 2 x 6 x 15 0
2
2
1 37
2
3 39
2
6
Правило чередования знаков здесь не работает, так как левая
часть не разложена на множители.
Браться за определение знаков функции методом контрольных
точек страшновато (хотя преодолев определенные
вычислительные трудности, мы достигнем цели).
Можно избежать этих неприятностей, если владеть другими
методами решения иррациональных неравенств.
Ответ :

8. 2.Метод замены переменной. Пример 3

9. 2.Метод замены переменной. Пример 4

10. 3.«Расщепление» неравенств.

Если левая часть неравенства представляет собой
произведение двух выражений, а правая равна нулю,
то схема решения неравенства опирается на правило
знаков при умножении (делении) положительных и
отрицательных чисел.
Пример 1.
Пример 2.
или
или

11.

Использование свойств квадратного корня.
1)
f ( x) 0,
f ( x) g ( x)
2)
f ( x) g ( x)
Методы
Пример 5.
20 x 2 x ( x 2 8 x 12 ) 0
Так как первый множитель (корень)
неотрицателен, следовательно не влияет на
знак правой части неравенства.
ОДЗ : 20 x 2 x 0
x [ 5 ;4 ]
Рассмотрим два случая.
1 случай.
20 x 2 x 0
x 5
В этом случае неравенство выполнено =>
- решения.
x 4
2 случай. 20 x 2 x 0 Тогда имеем право разделить обе части
неравенства на положительный множитель не меняя знак.
x 2 8 x 12 0
( x 2 )( x 6 ) 0
5
2
4
6
Учтем ОДЗ
Ответ : { 5 } [ 2 ;4 ]

12.

Использование свойств квадратного корня.
1)
f ( x ) 0,
f ( x ) g( x )
2)
f ( x ) g( x )
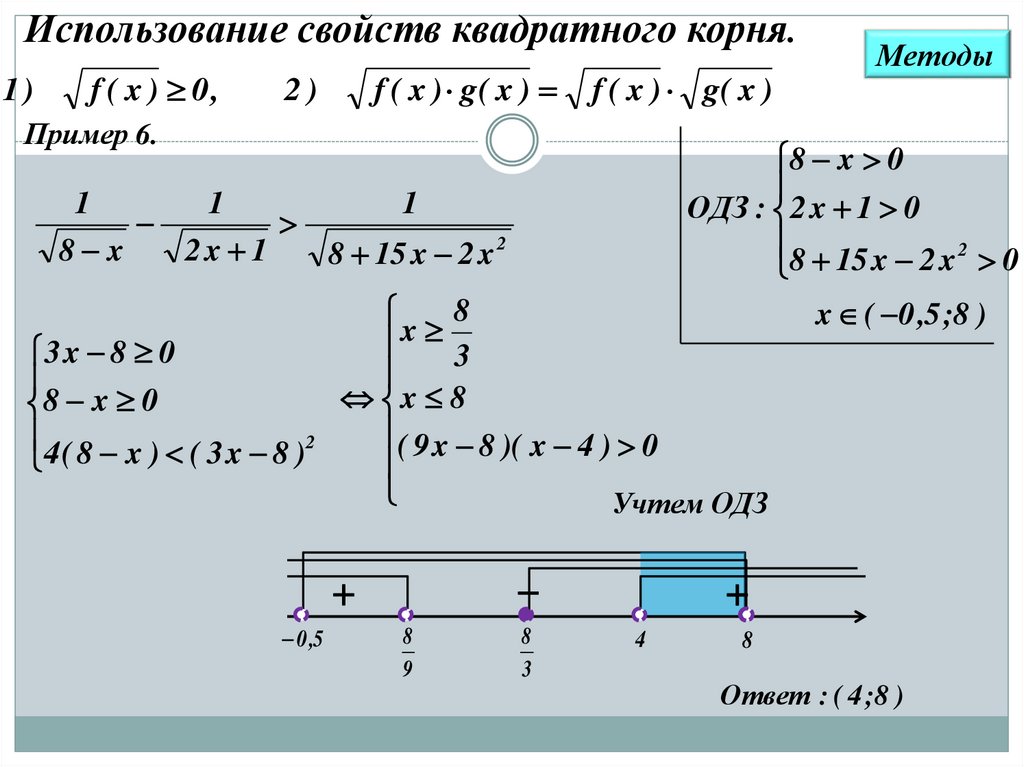
Пример 6.
8 x 0
ОДЗ : 2 x 1 0
8 15 x 2 x 2 0
1
1
1
8 x
2x 1
8 15 x 2 x 2
3 x 8 0
8 x 0
4 ( 8 x ) ( 3 x 8 )2
8
x 3
x 8
( 9 x 8 )( x 4 ) 0
Учтем ОДЗ
0 ,5
8
9
Методы
8
3
x ( 0 ,5 ;8 )
4
8
Ответ : ( 4 ;8 )

13. «Расщепление» неравенств. Примеры.

1.
2.
3.

14. 4. Метод рационализации.

Метод рационализации заключается в замене
сложного выражения F(x) на более простое
выражение G(x) (в конечном счете рациональное), при которой неравенство G(x)
равносильно неравенству F(x)
в области
определения выражения F(x) .
Выделим некоторые выражения F и соответствующие им рационализирующие выражения G.

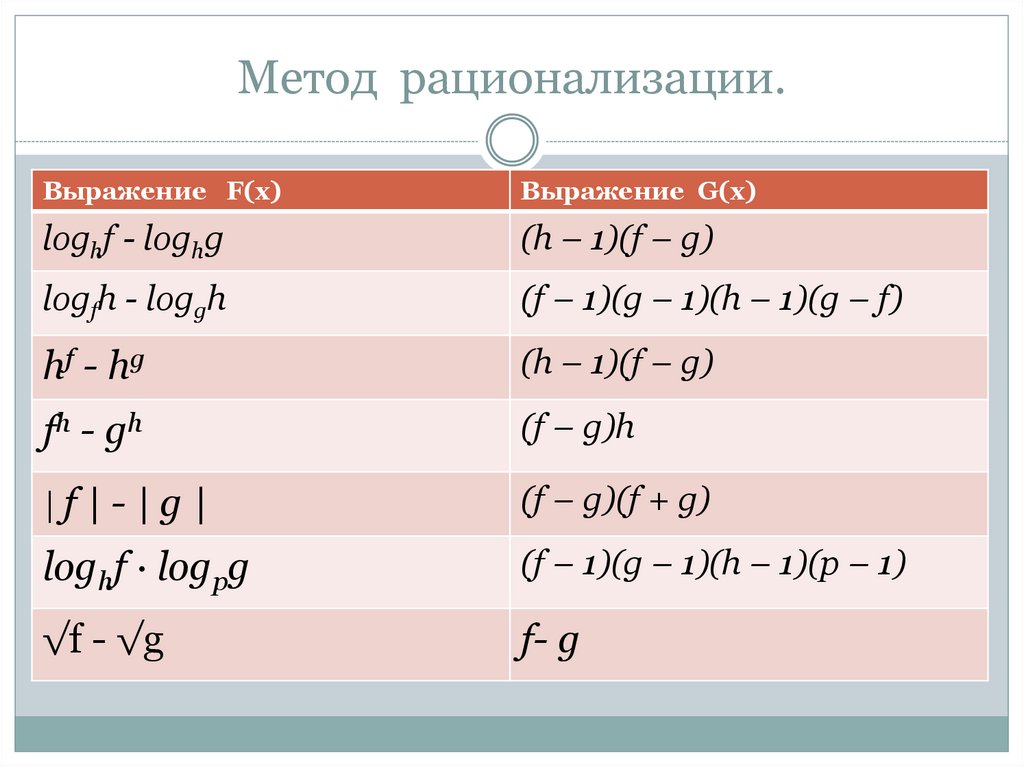
15. Метод рационализации.

Выражение F(x)
Выражение G(x)
loghf - loghg
(h – 1)(f – g)
logfh - loggh
(f – 1)(g – 1)(h – 1)(g – f)
hf - hg
(h – 1)(f – g)
fh - gh
(f – g)h
|f|-|g|
(f – g)(f + g)
loghf · logpg
(f – 1)(g – 1)(h – 1)(p – 1)
√f - √g
f- g

16.

Метод рационализации (замены множителей) Методы
Переходы
Пример 7.
3x 3x 7 6 x x
0
( 10 x 7 )( 10 x 3 )
2
2
Числитель является множителем дроби.
Замена:
f ( x ) g( x ) f ( x ) g( x )
3 x2 3 x 7 ( 6 x x2 )
0
( 10 x 7 )( 10 x 3 )
3 x2 3 x 7 ( 6 x x2 )
0
( 10 x 7 )( 10 x 3 )
4 x2 4 x 1
( 2 x 1 )2
0
0
( 10 x 7 )( 10 x 3 )
( 10 x 7 )( 10 x 3 )
2
0 ,3
!
0 ,5
Учтем ОДЗ
0 ,7
3
3 x 2 3 x 7 0
6 x x 2 0
ОДЗ
10 x 7 0
10 x 3 0
D 0, x R
( x 3 )( x 2 ) 0
x 0 ,7
x 0 ,3
2 0 ,3
0 ,7
3
Ответ : [ 2 ;0 ,3 ) { 0 ,5 } ( 0 ,7 ;3 ]

17.

Методы
Использование равносильных переходов.
Пример 8.
17
x 2 2 x 1 0
2 x 3 0
2
x 2x 1 2x 3
2 x 3 0
x 2 2 x 1 ( 2 x 3 )2
1 система
x 2 2 x 1 0
2 x 3 0
( x ( 1 2 ))( x ( 1 2 )) 0
x 1,5
1 2
1,5
1 2
x [ 1 2 ;1,5 )

18. 5.Использование свойств функции. 4.1. Исследование области определения функции.

Предварительный анализ области определения
функций, входящих в неравенство (ОДЗ
неизвестной), иногда позволяет получить
решение без преобразований.

19. 5.1. Исследование ОДЗ неизвестной. Примеры.

1.
2.
3.

20. 5.2. Использование ограниченности функции. Метод оценки.

Иногда неравенство
устроено так,
имеют место
.
что на всей ОДЗ неизвестной
неравенства
и
В этом случае:
а) решение неравенства
сводится к
нахождению тех значений , для которых
и
б) решение неравенства
сводится к
нахождению ОДЗ неизвестной неравенства.

21. 5.2. Использование ограниченности функции. Метод оценки.

Примеры.
1.
2.

22. 5.2. Использование ограниченности функции. Использование неотрицательности функций.

Пусть левая часть неравенства
есть сумма
нескольких функций
Установили, что каждая из этих функций
неотрицательна на своей области определения. Тогда
неравенство
равносильно системе уравнений
При тех же условиях неравенство
сводится
к нахождению области определения функции
.

23. 4.2. Использование ограниченности функции. Использование неотрицательности функций.

Примеры.
1.
2.

24. 5.3. Использование монотонности функции.

Если функция
возрастает на своей области
определения, то неравенство
на
ОДЗ равносильно неравенству
. .
Если функция
убывает на своей области
определения, то неравенство
на
ОДЗ равносильно неравенству
.

25. Использование монотонности. Примеры.

1.
2.
3.