1000210123

1. ОТНОШЕНИЕ ПЛОЩАДЕЙ ПОДОБНЫХ ТРЕУГОЛЬНИКОВ геометрия – 8 класс

2.

1. Записать в тетрадь тему урока
2. Разобрать устно Теорему на Слайде 3
3. Разобрать и записать решение задачи на Слайде 4
4. Разобрать устно задачу на Слайде 5
5. Выписать в тетрадь Формулы выделенные красным цветом
6. Выполнить тест по ссылке:
https://onlinetestpad.com/itsejrsrsl3hw

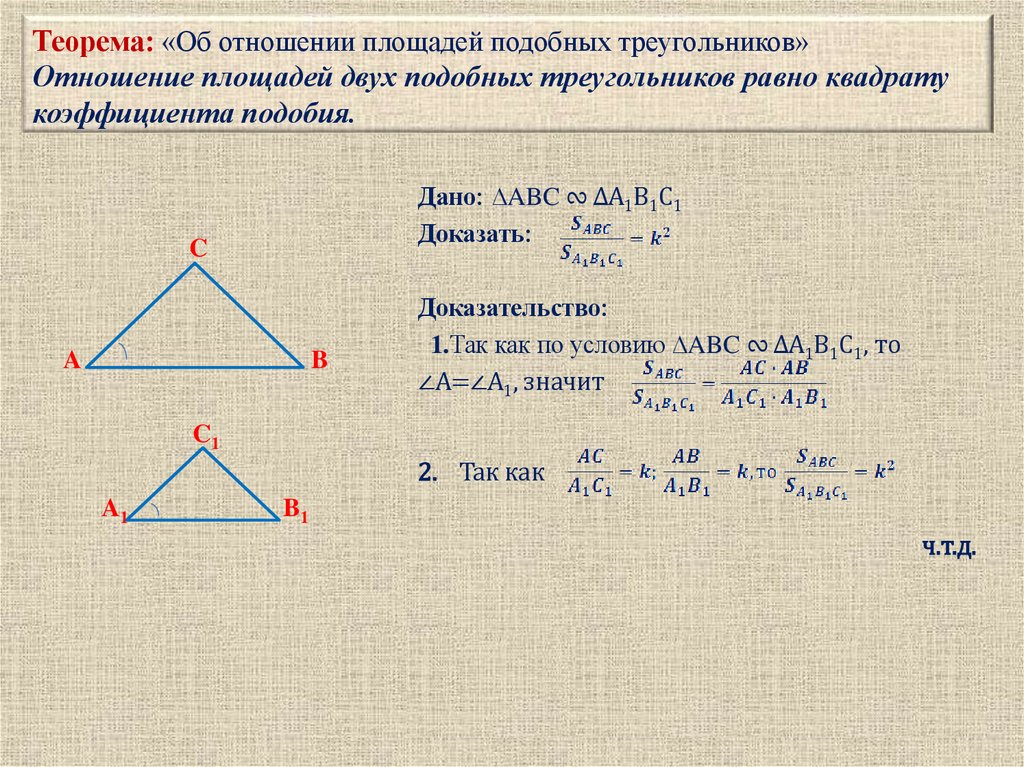
3. Теорема: «Об отношении площадей подобных треугольников» Отношение площадей двух подобных треугольников равно квадрату

коэффициента подобия.
Дано: ∆ABC ∾ ∆A1B1C1
Доказать:
C
A
B
Доказательство:
1.Так как по условию ∆ABC ∾ ∆A1B1C1, то
∠A=∠A1, значит
C1
2. Так как
A1
B1
ч.т.д.

4. Закрепление.

Дано: ∆ABC ∾ ∆A1B1C1,
Найти: AC
Решение:
B
A
1.Так как по условию
то по т. «Об отношении площадей подобных
треугольников»:
C
B1
A1
2.Так как : ∆ABC ∾ ∆A1B1C1, а также
AC и A1C1 – сходственные стороны, k=2, то
C1
Ответ: AC=4,5 (м)

5.

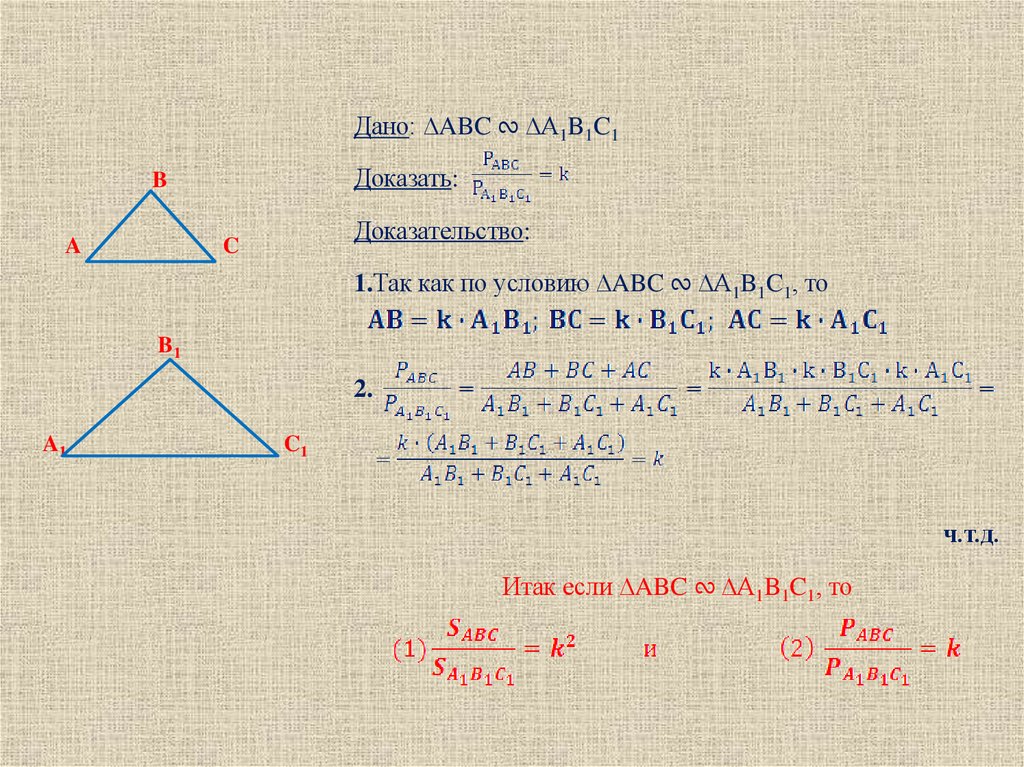
Дано: ∆ABC ∾ ∆A1B1C1
Доказать:
B
A
Доказательство:
C
1.Так как по условию ∆ABC ∾ ∆A1B1C1, то
B1
2.
A1
C1
ч.т.д.
Итак если ∆ABC ∾ ∆A1B1C1, то