Похожие презентации:
Второй и третий признаки подобия треугольников (8 класс)
1. Второй и третий признаки подобия треугольников
2. Вспоминаем то, что знаем
3.
Определение подобных треугольниковПервый признак подобия треугольников
Отношение площадей подобных
треугольников
Начать изучение нового
4.
BА
С
B1
С1
А1
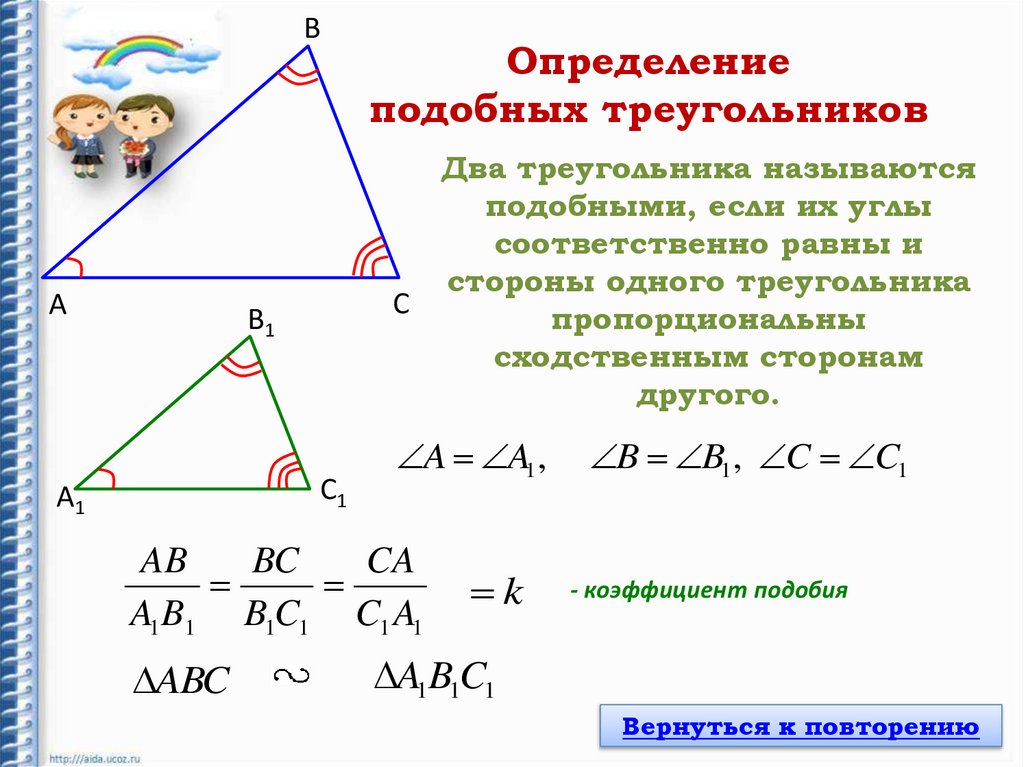
Определение
подобных треугольников
A A1 ,
AB
BC
CA
A1 B1 B1C1 C1 A1
ABC
Два треугольника называются
подобными, если их углы
соответственно равны и
стороны одного треугольника
пропорциональны
сходственным сторонам
другого.
k
B B1 , C C1
- коэффициент подобия
A1B1C1
Вернуться к повторению
5.
Первый признак подобиятреугольников
B
Если два угла одного треугольника
соответственно равны двум углам
другого треугольника, то такие
треугольники подобны.
С
А
Дано: A A1
B B1
B1
Доказать:
А1
С1
ABC
A1B1C1
Вернуться к повторению
6.
Отношение площадей подобныхтреугольников
B
Отношение площадей двух подобных
треугольников равно квадрату
коэффициента подобия.
S
С
А
ABC
A1B1C1
B1
AB
CD
CA
k
A1 B1 C1 D1 C1 A1
S1
А1
С1
S
k2
S1
Вернуться к повторению
7. Открываем новые знания
8.
Второй признак подобия треугольниковТретий признак подобия треугольников
Начать развивать умения
9.
Второй признак подобиятреугольников
ЕСЛИ ДВЕ СТОРОНЫ ОДНОГО
ТРЕУГОЛЬНИКА ПРОПОРЦИОНАЛЬНЫ
ДВУМ СТОРОНАМ ДРУГОГО
ТРЕУГОЛЬНИКА И УГЛЫ, ЗАКЛЮЧЕННЫЕ
МЕЖДУ ЭТИМИ СТОРОНАМИ, РАВНЫ, ТО
ТАКИЕ ТРЕУГОЛЬНИКИ ПОДОБНЫ.
С
А
B
Дано: AB AC
A1 B1
Доказать:
ABC
С1
A1C 1
A A1
A1B1C1
Доказательство
А1
B1
Вернуться к изучению нового
10.
Вернуться к изучению новогоДоказательство второго признака
подобия треугольников
1. Построим
С
А
1
2
С2
ABC 2 так, что
1 A1 , а 2 B1 .
2. 1 A1 , а 2 B1 , значит
B
ABC 2
A1B1C1 - по первому признаку
подобия треугольников.
AB
AC2
AB
AC
3.
и
, поэтому
С1
A1 B1 A1C 1
A1 B1 A1C 1
AC AC2 , значит ABC ABC2 , B 2.
,
4. B 2 , 2 B1 , значит B B1.
А1
B1 5. A A1 , B B1, A1 B1C1
ABC .
11.
Третий признак подобиятреугольников
ЕСЛИ ТРИ СТОРОНЫ ОДНОГО
ТРЕУГОЛЬНИКА ПРОПОРЦИОНАЛЬНЫ
ТРЕМ СТОРОНАМ ДРУГОГО, ТО ТАКИЕ
ТРЕУГОЛЬНИКИ ПОДОБНЫ.
С
А
B
Дано: AB BC CA
A1 B1
B1C1
Доказать: ABC
С1
C1 A1
A1B1C1
Доказательство
А1
B1
Вернуться к изучению нового
12.
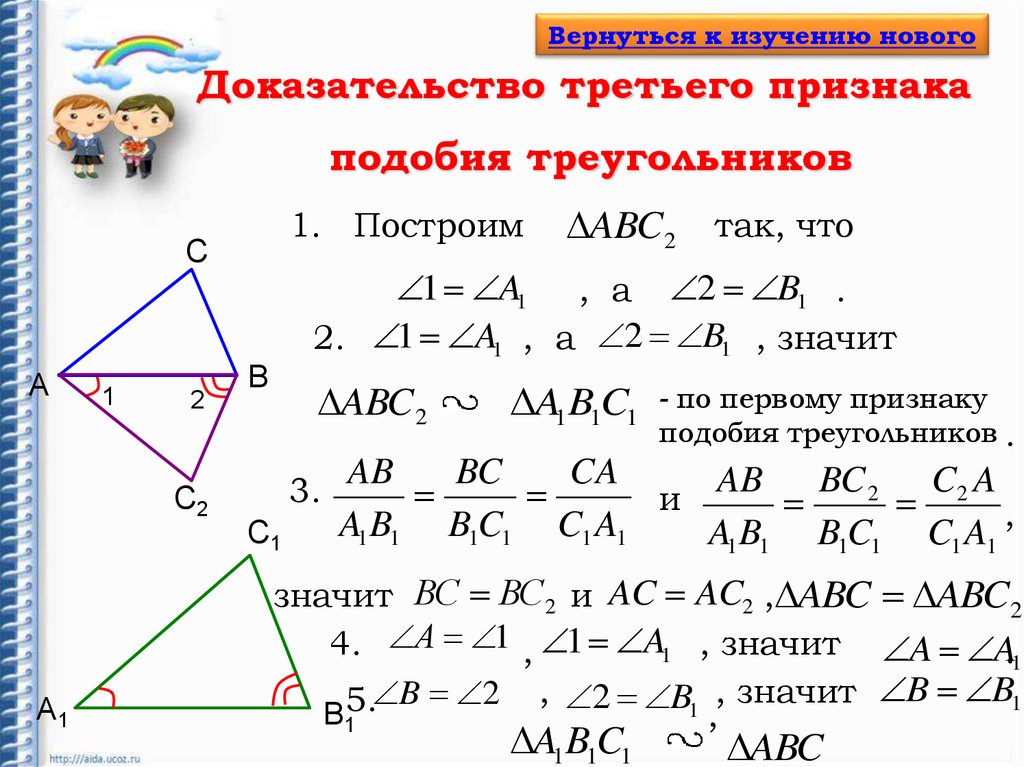
Вернуться к изучению новогоДоказательство третьего признака
подобия треугольников
1. Построим
С
А
1
2
С2
А1
ABC 2 так, что
1 A1 , а 2 B1 .
2. 1 A1 , а 2 B1 , значит
B
ABC 2
A1B1C1 - по первому признаку
подобия треугольников .
AB
BC
CA
AB BC 2 C2 A
3.
и
A1 B1 B1C1 C1 A1
С1
A1 B1 B1C1 C1 A1 ,
значит ВC ВC2 и AC AC2 , ABC ABC2
4. А 1 , 1 A1 , значит A A.1
B 2 , 2 B1 , значит B B1
5.
B1
,
A1B1C1
ABC
13. Развиваем умения
14.
Решите устно:в
Р
35˚
8
10
35˚
4
А
С
М
5
К
15.
Решите устно:в
Р
25˚
25˚
А
С
М
К
16.
Решите устно:в
32
А
Р
40
24
С
4
5
М
3 К
17.
Решите устно:в
36
20
18
А
9
С
М
10
18.
Решите письменно:19.
Решите письменно:М
В
5 cм
3,6 см
А
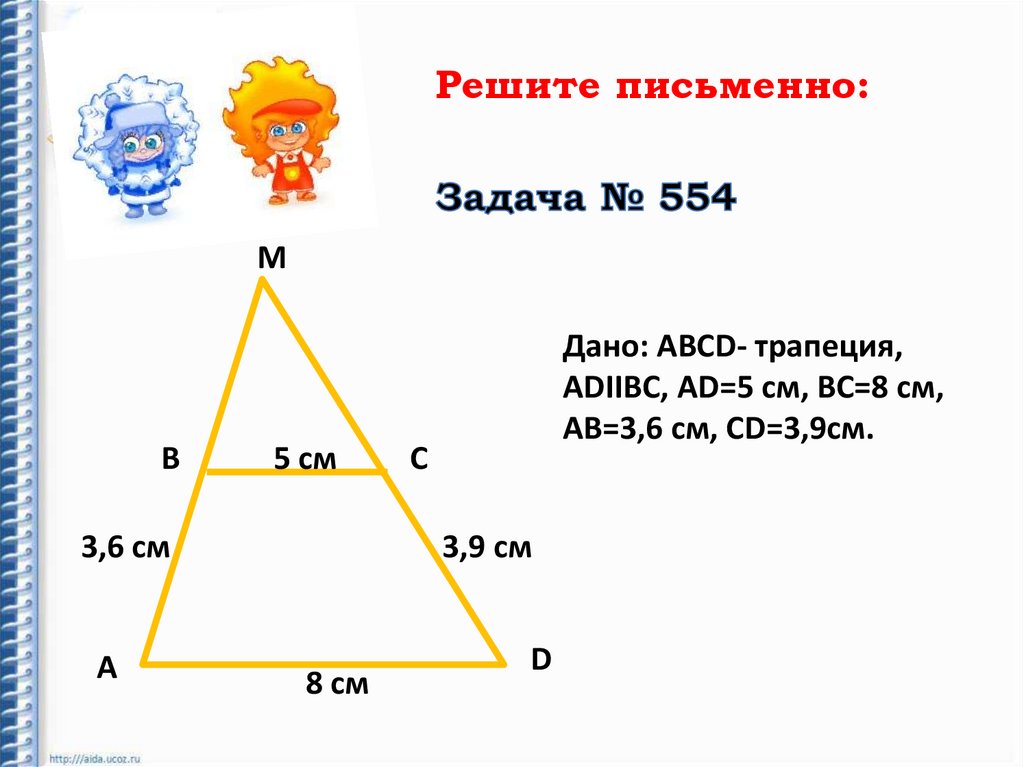
Дано: АВСD- трапеция,
АDIIВС, АD=5 см, ВС=8 см,
АВ=3,6 см, СD=3,9см.
С
3,9 см
8 см
D
20.
Решите письменно:М
В
5 cм
Дано: АВСD- трапеция,
АDIIВС, АD=5 см, ВС=8 см,
АВ=3,6 см, СD=3,9см.
С
Найти: МВ, МС.
3,6 см
3,9 см
Решение:
А
8 см
D
21.
Решите письменно:М
В
5 cм
3,6 см
А
8 см
Решение:
1) ∆ АМD
∆ ВМС по
первому признаку
(<М – общий, <В = <А , т к
соответственные при
С
пересечении
параллельных прямых
АD и ВС секущей АВ).
3,9 см
2) Из подобия ∆ АМD и
∆ ВМС следует, что
D АD
АМ = МD
=
ВС
ВМ
МС
22.
Решите письменно:М
х см
В
5 cм
3,6 см
А
8 см
Решение:
3) Пусть ВМ – х см, тогда
(х + 3,6) см – АМ.
х + 3,6 8
=
х
5
С
5( х + 3,6) = 8х
5х + 18 = 8х
3,9 см 5х – 8х = -18
-3х = -18
х = 6 (см) - МВ
D
23.
Решите письменно:М
х см
В
3,6 см
А
Решение:
4) Пусть СМ – у см, тогда
(у + 3,9) см – МD.
у см
у + 3,9 8
=
у
5
5 cм
С
5( у + 3,9) = 8у
5у + 19,5 = 8у
3,9 см 5у – 8у = -19,5
-3у = -19,5
у = 6,5 (см) – МС
D
8 см
Ответ: 6 см и 6,5 см.
24.
Домашнее задание:25.
Вопросы к уроку:Какие треугольники
называются подобными?
Чему равно отношение площадей
подобных треугольников?
Сформулируйте признаки
подобия треугольников.























 Математика
Математика








