Похожие презентации:
3b0ca83b9e954f4299081092fe364b00
1.
2.
1. Простейшие (поопределению)
2. Метод
потенцирования.
Логарифмические уравнения
3. Метод введения
новой переменной
4. Преобразование по
формулам
2
3.
Решим следующие уравнения:3
8
а) log2(7-8х)=2
б) log 1 (3х 1) log 1 (6 х 10)
2
2
3
4.
log а f ( x) log а g ( x),где
a 0, a 1
f ( x) g ( x),
f ( x) 0 и g ( x ) 0
4
5.
• Ликвидировать (потенцировать)логарифмы можно, если у них:
• а) одинаковые числовые основания
• в) логарифмы слева - справа чистые (безо
всяких коэффициентов) и находятся в
гордом одиночестве.
• Итак, убирать логарифмы можно, если
уравнение выглядит так и только так:
logа(.....) = logа(.....)
5
6.
Пример 1log 1 (3х 1) log 1 (6 х 10)
2
(3х 1) 0 3х 1
(6 х 10) 0 6 х 10
х
х
1
3
5
3
3х 1 6х 10 3х 9
2
х
х 3
5
3
3
6
7.
Пример 2Решите уравнение
ОДЗ:
2 x 4 0,
х 1 0;
2 х 4 х 1,
log 2 (2х 4) log 2 ( x 1).
x 2,
x 1.
2 х х 1 4,
x 2.
х 3.
x 3 удовлетворяет условию x 2, следовательно, x 3
является корнем исходного уравнения.
Ответ : 3.
8.
Пример 2Решите уравнение
log 2 (2х 4) log 2 ( x 1).
2 х 4 х 1, 2 х х 1 4,
Проверка:
Если х 3, то
х 3.
log 2 (2 3 4) log 2 (3 1),
log 2 (6 4) log 2 2, log 2 2 log 2 2,
1 1 верно.
Ответ : 3 .
9.
Решим следующее уравнение:2
lg(х -2) = lg х
2
9
10. Самостоятельное решение заданий
1) log3х = log392) log7(2х-3) = log7х
3) log 5 (2x+3)= log 5 (x+1)
4) log 4 x= log 4 (6-x2)
5) log 0,3 (-x 2 +5x+7)= log 0,3
9
3
Нет
решени
я
2
(10x-7)
2
10
11. Домашняя работа
.1) log2(x + 3) = log216
2) log 1 x 2 3x 1 2
3
3) log4(х+3) = log4(4x – 15)
4) lg(х2 – 2х) = lg (2х + 12)
2
2
x
lg
8
9
x
5) lg
6) (log2x) 2 -5 log2x +6 = 0
11







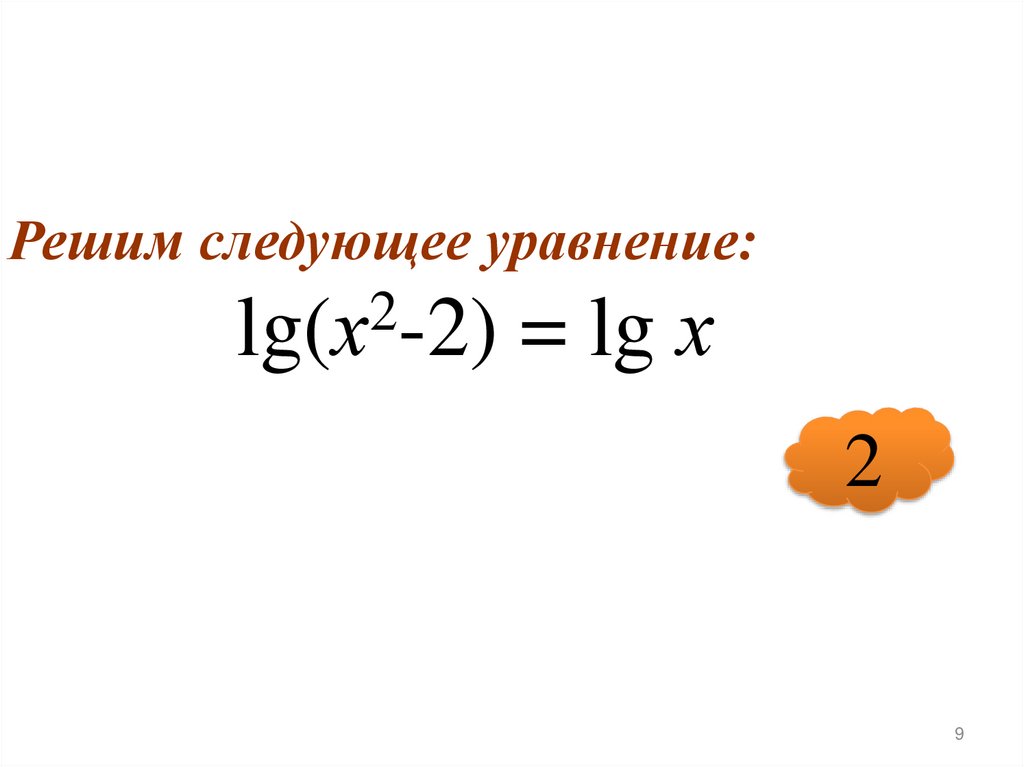


 Математика
Математика








