Похожие презентации:
Определение логарифма. Основное логарифмическое тождество
1.
2. Определение логарифма
ОПРЕДЕЛЕНИЕ ЛОГАРИФМАb 0
a 0
log a b x
a
1
x
b a
3. Основное логарифмическое тождество
ОСНОВНОЕ ЛОГАРИФМИЧЕСКОЕ ТОЖДЕСТВОa
loga b
b
4. Основные свойства логарифмов
ОСНОВНЫЕ СВОЙСТВА ЛОГАРИФМОВa>0,b>0,c>0, c≠1,n≠1
log a 1 0
x
log a log a x log a y
y
log a a 1
log a x n log a x
n
log a ( xy) log a x log a y
5.
Формула перехода от одного основанияк другому
log a x
6.
Формула перехода от одного основанияк другому
log b x
log a x
,
log b a
b 1, b 0, x 0, a 0, a 0
7.
Чему равны:log 4 16
lg 100
log 3 27
lg 0,001
log 5 125
log3 8
3
8. Дайте определение логарифмической функции
ДАЙТЕ ОПРЕДЕЛЕНИЕ ЛОГАРИФМИЧЕСКОЙФУНКЦИИ
y log a x
Каковы область определения и область
значений функции у = log а х и их
обозначения ?
Свойства монотонности : в каком
случае функция у = loq а х является
возрастающей, в каком убывающей?
Найдите выражения, имеющие смысл:
log 5 0; log 2 (-4) ; log 5 1 ; log 5 5.
9.
10.
Цель:Познакомиться со способами
решения логарифмических
уравнений. Научиться применять
их при решении логарифмических
уравнений.
11.
Скажи мне – и я забуду,Покажи мне – и я запомню,
Дай мне действовать самому
– и я научусь.
Древнекитайская мудрость
12.
Что значит «решить уравнение»?Решить уравнение – это значит найти все его
корни (решения) или установить, что их нет.
13.
Что такое корень уравнения?Корнем (решением) уравнения называется
число, которое при подстановке в уравнение
превращает его в верное равенство.
14.
Какие уравнения называютлогарифмическим?
Логарифмическим уравнением – уравнение,
содержащие неизвестное под знаком логарифма.
15.
Определение простейшегологарифмического
уравнения:
Уравнение вида log а х = в, где а ≠ 1 , а > 0 , х > 0,
называется простейшим логарифмическим уравнением,
оно равносильно уравнению х = ав, причём ни
проверка, ни ОДЗ не требуется.
Простейшие логарифмические уравнения:
1. logх-18 = 1
2. log7(50х-1) = 2
3. log3х = log39
4. log7(2х-3) = log7х
16.
При решении логарифмических уравненийчасто используются следующие методы:
Метод решения с помощью определения логарифма
Применение основного логарифмического тождества
Метод потенцирования
Метод введения новых переменных;
Метод логарифмирования
Метод приведения логарифмов к одному и тому же
основанию.
Графический метод.
17.
Метод решения с помощью определениялогарифма
Например,
уравнение log а х = b (а > 0, а≠ 1, х>0 )
имеет решение X= ab
1.
ПРИМЕРЫ:
1) log 4 x=2
x=16
2) log 0,5 x=2
x=0,25
3) log x 5=1
X=5
4) log 5 x=-2
X=0,04
18.
Метод решениялогарифма
ПРИМЕР:
1.
5) logх-18 =1
Решение:
(х-1)1 = 8
х-1 = 8
х=9
с
помощью
определения
19.
1.Метод решения
логарифма
ПРИМЕР:
с
помощью
6) log7(50х-1) = 2
Решение:
72 = 50х-1
50х-1 = 49
х=1
определения
20.
2. Применение основного логарифмическоготождества: alog a b =b (где b>0, a>0 и a≠1)
Примеры: 1) 9x =0,7
Решение:
9x =0,7
9x =9 log 90,7
X= log 90,7
2) 2x =10
2x =10
2x =2 log 210
X= log 210
3) 0,3x =7
0,3x =7
0,3x =0,3 log 0,37
X= log 0,37
21.
3. Метод потенцированияСуть метода- переход от уравнения log а f( х)= log а
φ(х)
к уравнению следствию
f(х)=φ(х). При
решении уравнений log a f(x) = log a φ(х) часто
происходит расширение области определения
уравнения (за счёт решения уравнения f(х)=φ(х)),а
значит, могут появиться посторонние корни.
Поэтому, решив уравнение, следует проверить
найденные корни подстановкой в данное уравнение.
22.
3. Метод потенцированияЛиквидировать (потенцировать) логарифмы безо всяких
опасений можно, если у них:
а) одинаковые числовые основания
в) логарифмы слева - справа чистые (безо всяких
коэффициентов) и находятся в гордом одиночестве. Это
значить, в уравнении log3х =2log3(3х-1) убирать
логарифмы нельзя, так как двойка справа не позволяет.
Коэффициент.
В примере log3х+log3(х+1) = log3(3+х) тоже
нельзя потенцировать уравнение. В левой части нет
одинокого логарифма. Их там два.
Итак, убирать логарифмы можно, если уравнение
выглядит так и только так: logа(.....) = logа(.....)
23. Физкультминутка
ФИЗКУЛЬТМИНУТКА24. Примеры на метод потенцирования
ПРИМЕРЫ НА МЕТОД ПОТЕНЦИРОВАНИЯ1) log3х = log39
Решение: 1) х=9 Проверка: подставим
найденное значение x=9 в исходное
уравнение log39 = log39
Ответ: х=9
25. Примеры на метод потенцирования
ПРИМЕРЫ НА МЕТОД ПОТЕНЦИРОВАНИЯ2) log7(2х-3) = log7х
Решение: 2х-3=х; х=3 Проверка: подставим
найденное значение x=3 в исходное
уравнение log7(2.3-3) = log73;
log73 = log73
Ответ: х=3
26. Примеры на метод потенцирования
ПРИМЕРЫ НА МЕТОД ПОТЕНЦИРОВАНИЯ3) log 5 (2x+3)= log 5 (x+1)
Решение: log 5 (2x+3)= log 5 (x+1)
2x+3= x+1; x=1-3=-2
Проверка: подставим найденное значение x= -2 в
исходное уравнение log 5 (2x+3)= log 5 (x+1) и
получим log 5 (2 . (-2)+3)= log 5 (-2+1), log 5 (-1)=
log 5 (-1), это равенство неверно (оно не имеет
смысла, так как выражения под логарифмом
всегда больше нуля)
Ответ: нет решения
27. Примеры на метод потенцирования
ПРИМЕРЫ НА МЕТОД ПОТЕНЦИРОВАНИЯ4) log 5 x= log 5 (6-x2)
Решение:
log 5 x log 5 (6 x )
2
x 6 x
2
x2 x 6 0
x1 3
x2 2
Проверка:
1) x1 3
2)
x2 2
Ответ: 2.
log 5 ( 3) не существует -3 посторонний
корень
log 5 2 log 5 (6 2 2 )
log 5 2 log 5 2
28. 4. Метод введения новых переменных
4. МЕТОД ВВЕДЕНИЯ НОВЫХ ПЕРЕМЕННЫХСуть метода -приведение логарифмического
уравнения к квадратному A log 2 x B log x C 0
a
a
1) ввести новую переменную y log a x
2) решить уравнение Ay
2
By C относительно y;
3) выполнить обратную подстановку и решить
уравнения относительно х.
29. Метод введения новых переменных
МЕТОД ВВЕДЕНИЯ НОВЫХ ПЕРЕМЕННЫХПример: 1) 2 log 2 x 5 log
log 5 x y
5
5
x 2 0
2 y2 5 y 2 0
D 25 16 9 3
2
5 3
1
y1 , 2
y1 2, y2
2 2
2
log 5 x 2
x 5
2
1
25
1
log 5 x
2
1
1
2
x 5
5
Ответ:
1
25
;
1
5
30. Метод введения новых переменных
МЕТОД ВВЕДЕНИЯ НОВЫХ ПЕРЕМЕННЫХРешение: 2)
lg x lg x 1 0
2
2
lg x 2 lg x 1 0
lg x y
2
y2 2 y 1 0
D 0
b
y
2a
,
y 1
lg x 1
x 10
Ответ: 10
31. 1.Решите уравнения методом потенцирования:
ЗакреплениеВариант 1. № 1 (а)
№2 (а)
Вариант 2. №1 (б)
№2 (б)
1.РЕШИТЕ УРАВНЕНИЯ МЕТОДОМ ПОТЕНЦИРОВАНИЯ:
а) log2 (3x – 6) = log2 (2x – 3);
б) log6 (14 – 4x) = log6 (2x + 2);
2. Решите уравнения методом введения вспомогательной
переменной:
2
05
x 5 log 0,5 x 2 0;
2
0,3
x 7 log 0,3 x 4 0.
а) 3 log
б)
2 log
32.
Домашнее задание:№№ 512(г), 513 (а, в), 514 (а, в)
33. Пожалуйста, с помощью карточек, оцените вашу деятельность на уроке.
ПОЖАЛУЙСТА, С ПОМОЩЬЮ КАРТОЧЕК,ОЦЕНИТЕ ВАШУ ДЕЯТЕЛЬНОСТЬ НА УРОКЕ.
Я все понял и смогу применить
полученные знания на практике.
Я практически все понял, но
испытываю затруднения в
применении полученных знаний на
практике.
Плохо понял тему и не смогу
применить на практике.






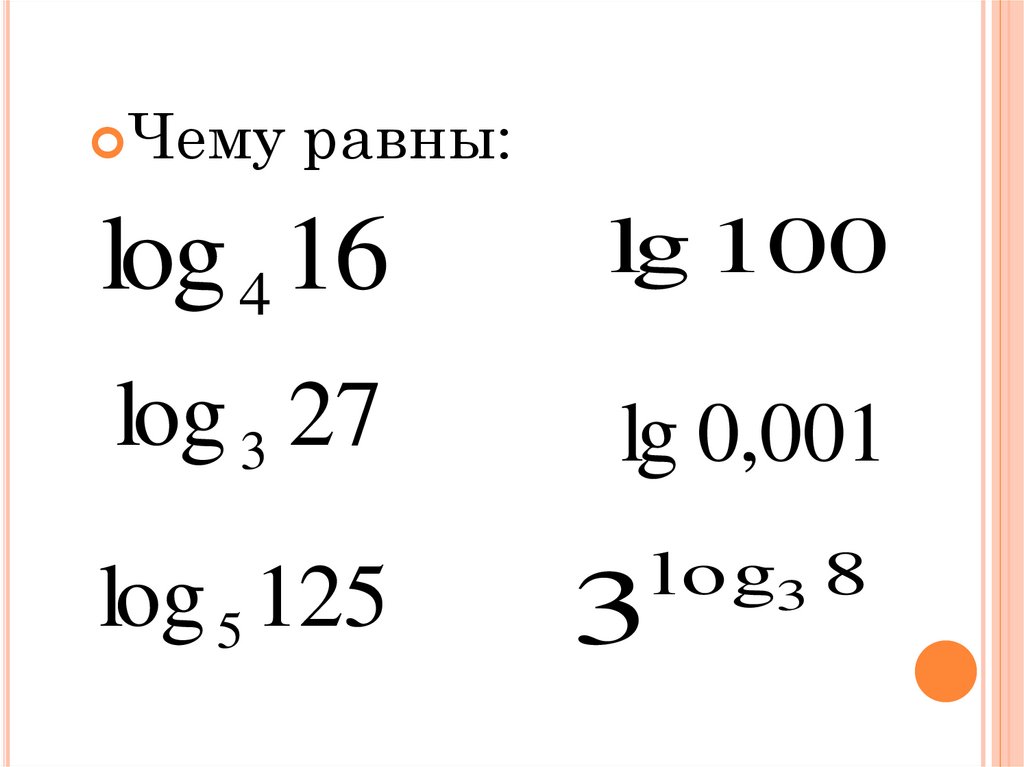



























 Математика
Математика








