10 вектори у просторі

1.

ВЕКТОРИ
У ПРОСТОРІ
Дії над векторами
(10 клас)

2. Повторення

3. Поняття вектора

Вектор - це величина, яка
а
а
АВ, АВ, а, а
АА
АА 0
характеризується числовим
значенням і напрямком.
Вектор - напрямлений
відрізок.
Під направленим
відрізком розуміють
впорядковану пару точок, перша
з яких - точка A - називається
його початком, а друга - B його кінцем.

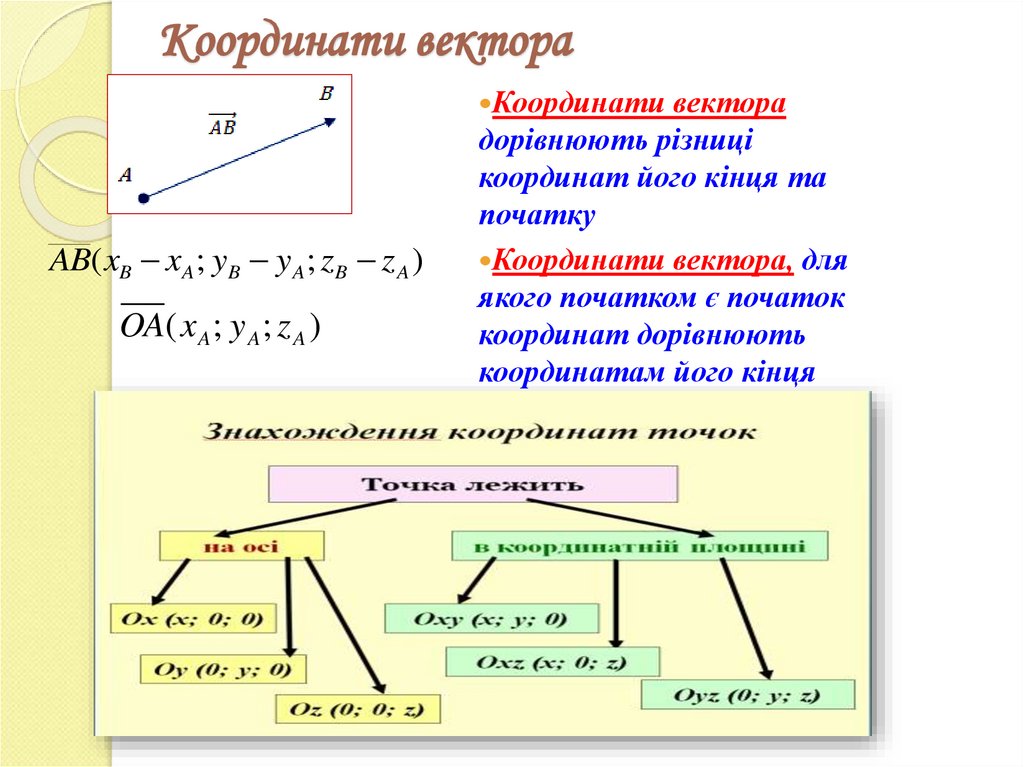
4. Координати вектора

Координати вектора
AB( xB xA ; yB y A ; zB z A )
OA( x A ; y A ; z A )
дорівнюють різниці
координат його кінця та
початку
Координати вектора, для
якого початком є початок
координат дорівнюють
координатам його кінця

5. Напрямленість векторів

Вектори
і
називають протилежно
напрямленими, якщо
протилежно напрямлені
півпрямі AB і CD .
Вектори
і
називають
співнапрямленими,
якщо співнапрямлені
півпрямі AB і CD.

6.

7. Абсолютна величина вектора

AB x
2
AB
y
2
AB
z
2
AB
a x y z
2
a
2
a
0 0
2
a
Абсолютна величина
вектора
( модуль вектора,
довжина вектора)
дорівнює кореню
квадратному із
суми квадратів його
координат

8.

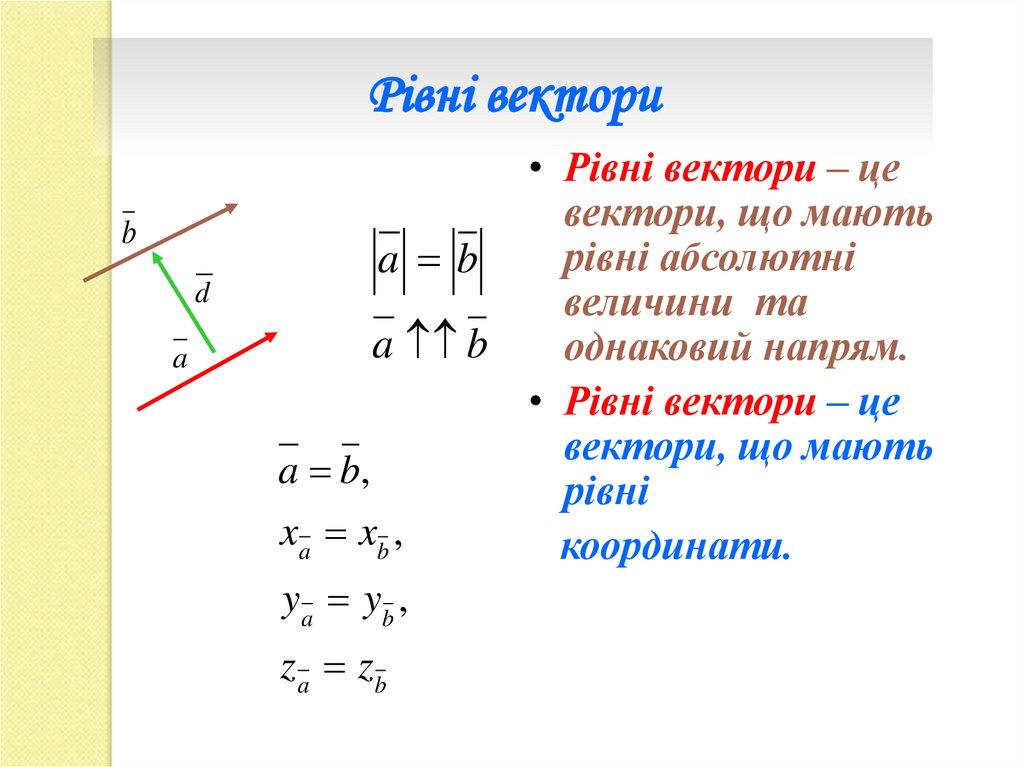
Рівні вектори
b
d
a
• Рівні вектори – це
вектори, що мають
рівні абсолютні
a b
величини та
a b
однаковий напрям.
• Рівні вектори – це
вектори, що мають
a b,
рівні
xa xb ,
координати.
y a yb ,
z a zb

9.

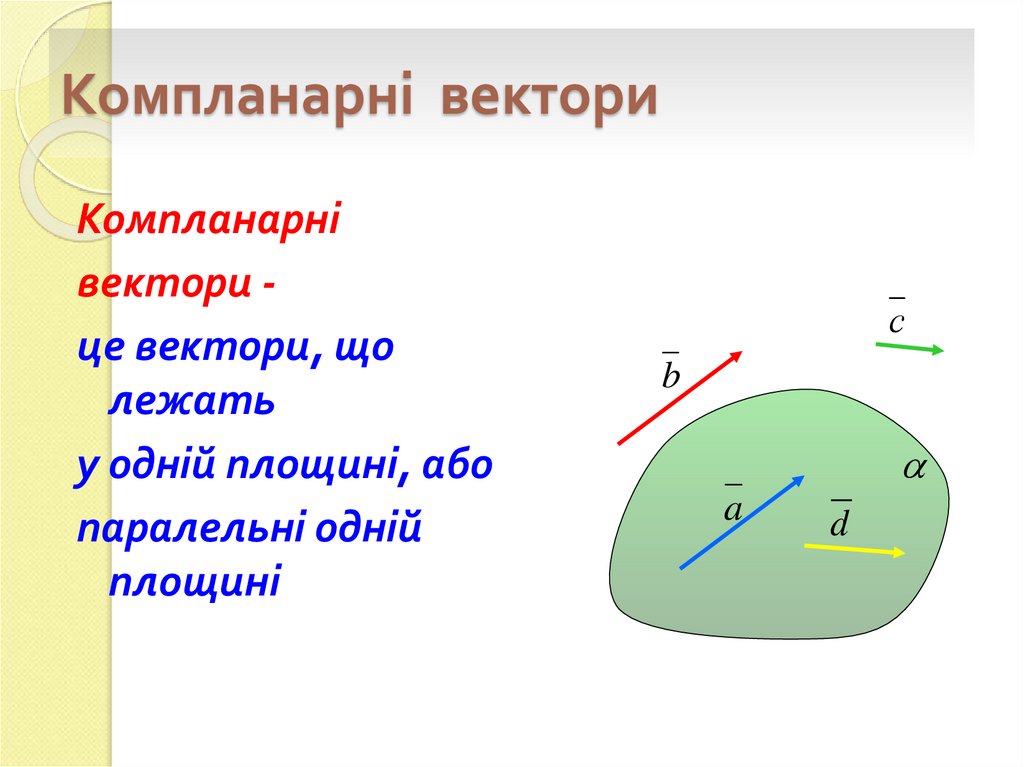
10. Компланарні вектори

Компланарні
вектори це вектори, що
лежать
у одній площині, або
паралельні одній
площині
с
b
a
d

11.

12.

13.

а
b
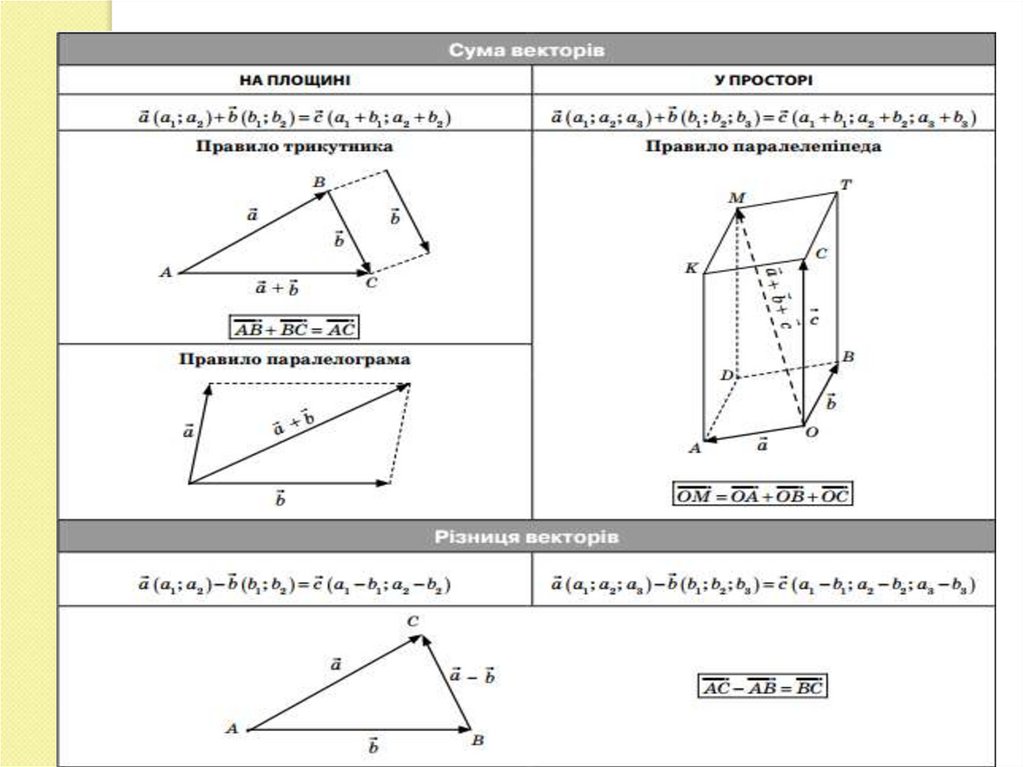
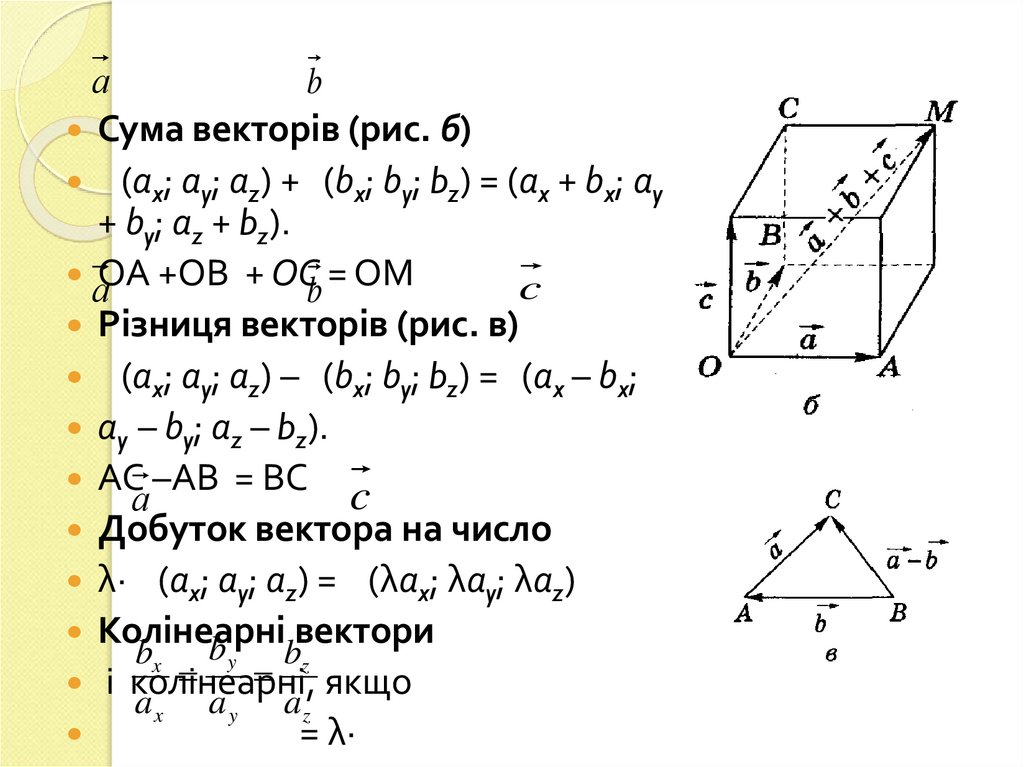
Сума векторів (рис. б)
(аx; аy; аz) + (bx; by; bz) = (аx + bx; аy
+ by; аz + bz).
ОА +ОВ + ОС = ОМ
c
а
b
Різниця векторів (рис. в)
(аx; аy; аz) – (bx; by; bz) = (аx – bx;
аy – by; аz – bz).
АС –АВ = ВС
c
а
Добуток вектора на число
λ· (аx; аy; аz) = (λаx; λаy; λаz)
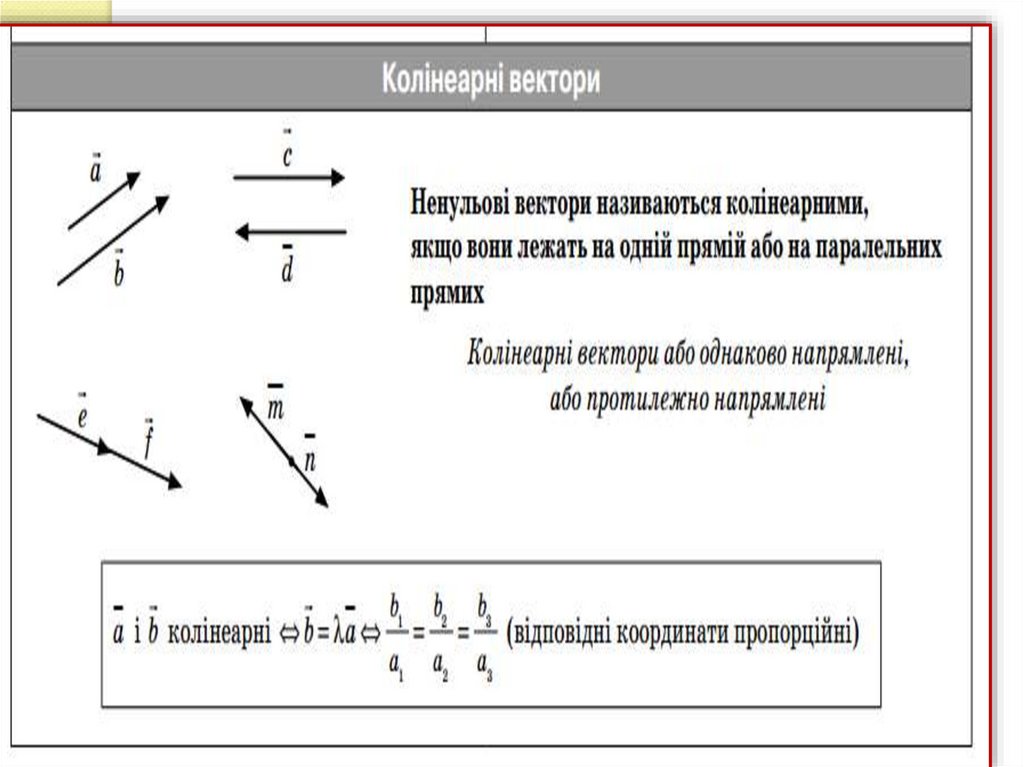
Колінеарні вектори
bx by bz
якщо
і колінеарні,
ax a y az
= λ·

14.

Приклад . Існують точки А(2; 0; 1), В(3; 5; 0), С(-1; 2; 3).
Знайти координати вектора n 2 AB 3BC.
Розв’язання.
Знайдемо координати векторів:
ВС 1 1; 2 5; 3 - 0 4; 3; 3 .
АВ 3 2; 5 0; 0 1 1; 5; 1 ;
Скориставшись правилами виконання дій над векторами,
заданими координатами, маємо:
3ВС 3 4; 3; 3 12; 9; 9 .
n 2 АВ 3ВС 2; 10; - 2 12; 9; 9 14; 19; 11 .
2 АВ 2 1; 5; 1 2; 10; - 2 ;

15.

16.

Задача 1. Даноа (-1; 2; -3), b (2; -1; 3).
Знайдіть координати векторів
2 а
3b
2 а 3 b
1) 2а (2 ( 1); 2 2; 2 ( 3))
2 а 3 b
1) 2а ( 2; 4; 6)
2) 3b ( 3 2; 3 ( 1); 3 3)
2) 3b ( 6; 3; 9)
3) 2 а 3 b ( 2 ;4; 6) ( 6;3; 9)
3) 2 а 3 b ( 8;7; 15)
3) 2 а 3 b ( 2 ;4; 6) ( 6;3; 9)
3) 2 а 3 b (4;1;3)

17.

Задача2.Знайдіть , 2а
якщо
а(1,5; 2; 0)
2а (1,5 2) 2 (2 2) 2 (0 2) 2
2а 9 16 0 25 5
Чи колінеарні вектори а
(-18; -12; 15) і
b (12; 8; - 10) ?
bx by bz 12 8 10
2
ax a y az
6 4 5
Чи колінеарні вектори
а (6; 4; -5) і b (12; 8; - 10) ?
bx by bz
12
8
10 2
a x a y a z 18 12 15
3

18.

Задача 3. Чи колінеарні векториAB і CD , якщо
А(3; -2; 5), B(-1; 4; -7), C(1; 3; D(-3; 9; 18)?
AB (хВ – хА; уВ – уА; zВ – zА)
AB( 1 3; 4 2; 7 5)
CD( 3 1; 9 3; 18 6)
AB( 4; 6; 12)
CD( 4; 6; 12)

19.

20. Домашнє завдання

Самостійна робота: “Дії над векторами.”

21.

Дякую за
увагу