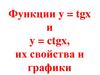ФУНКции

1.

2.

Степенными функциями
называются функции
вида у = хr, где r –
заданное
действительное число

3.

Показатель r = 2n – чётное натуральное число
у = х2, у = х4 , у = х6, у = х8, …
у
D( х) : x R
у = х2n
Е ( y) : у 0
0
График чётной функции
симметричен относительно
оси Оу.
х
Функция у=х2n чётная,
т.к. (–х)2n = х2n
Функция убывает на
промежутке
( ;0)
Функция возрастает
на промежутке (0; )

4.

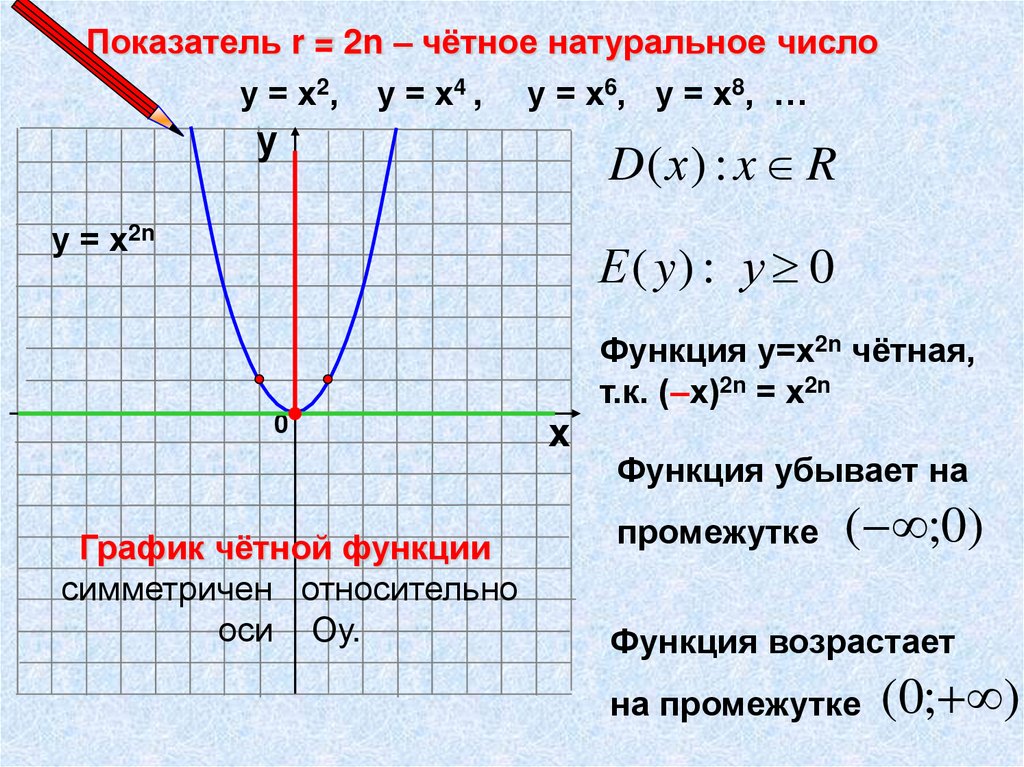
Показатель r = 2n-1 – нечётное натуральное число
у = х3, у = х5, у = х7, у = х9, …
у
D( х) : x R
Е ( y) : у R
у = х2n-1
Функция у=х2n-1 нечётная,
т.к. (–х)2n-1 = – х2n-1
0
х
Функция возрастает
на промежутке ;
График нечётной
функции симметричен
относительно начала
координат – точки О.

5.

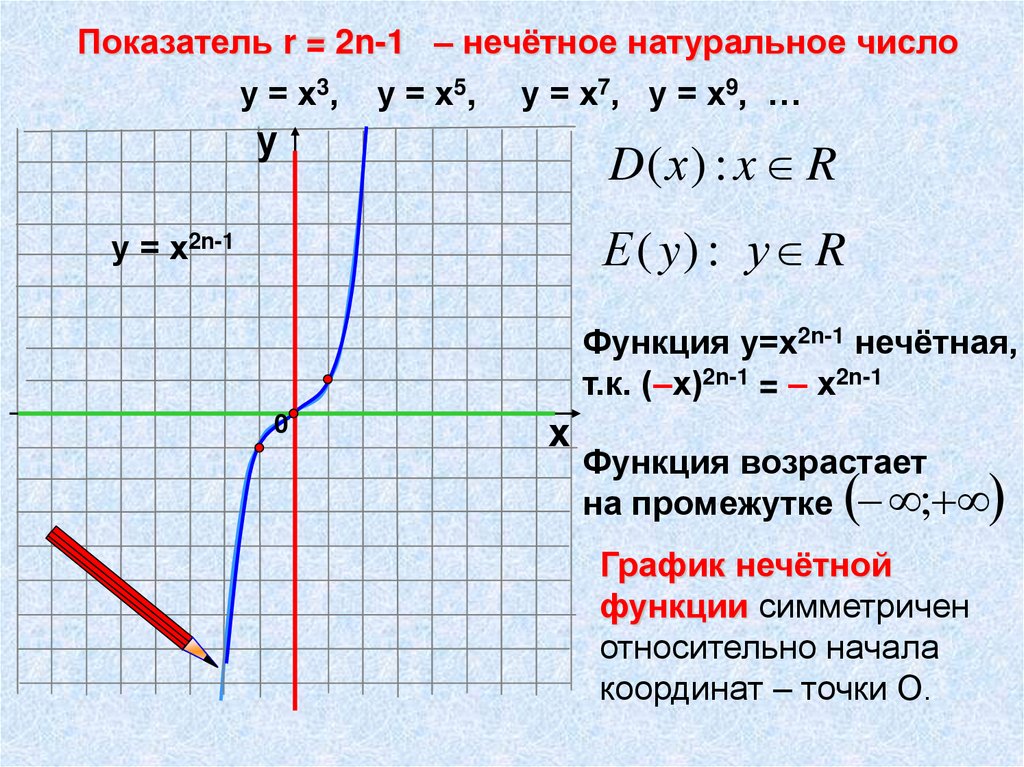
Показатель r = – (2n-1), где n – натуральное число
у = х-3, у = х-5 , у = х-7, у = х-9, …
у
D( х) : x 0
Е ( y) : у 0
0
y х
( 2 n 1)
Функция у=х-(2n-1)
нечётная,
–(2n-1) = –х–(2n-1)
т.к.
(–х)
х
1
y
х
1
Функция убывает на
2 n 1
промежутке
( ;0)
Функция убывает
на промежутке (0; )

6.

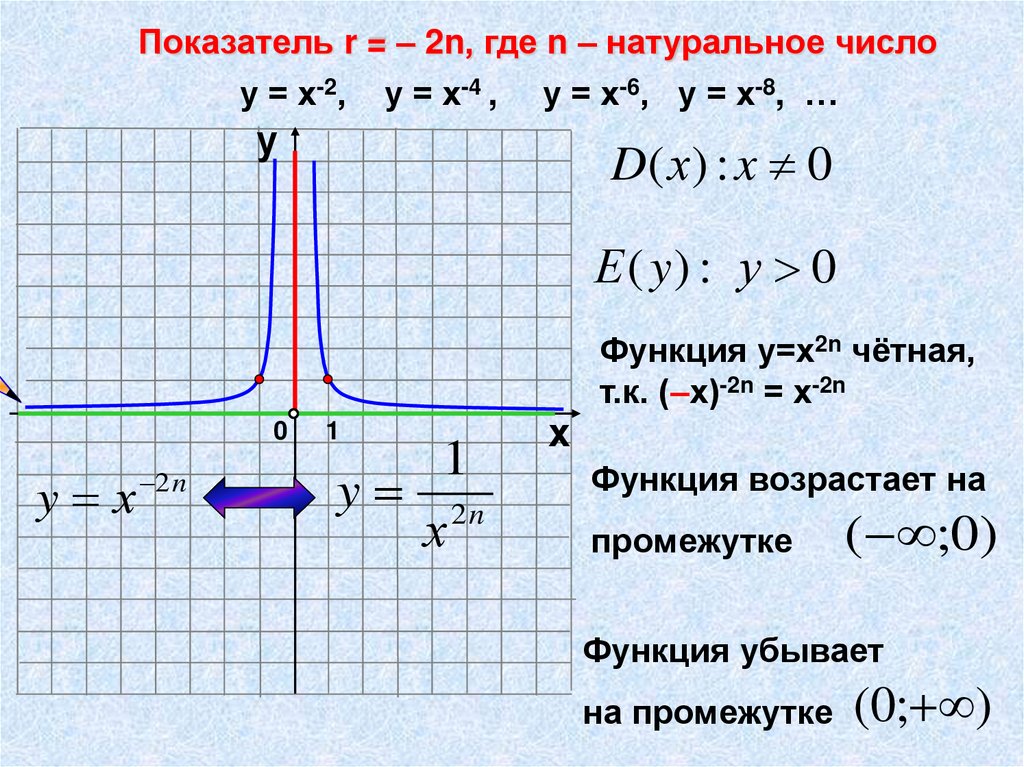
Показатель r = – 2n, где n – натуральное число
у = х-2, у = х-4 , у = х-6, у = х-8, …
у
D( х) : x 0
Е ( y) : у 0
0
y х
2 n
1
1
y 2n
х
х
Функция у=х2n чётная,
т.к. (–х)-2n = х-2n
Функция возрастает на
промежутке
( ;0)
Функция убывает
на промежутке (0; )

7.

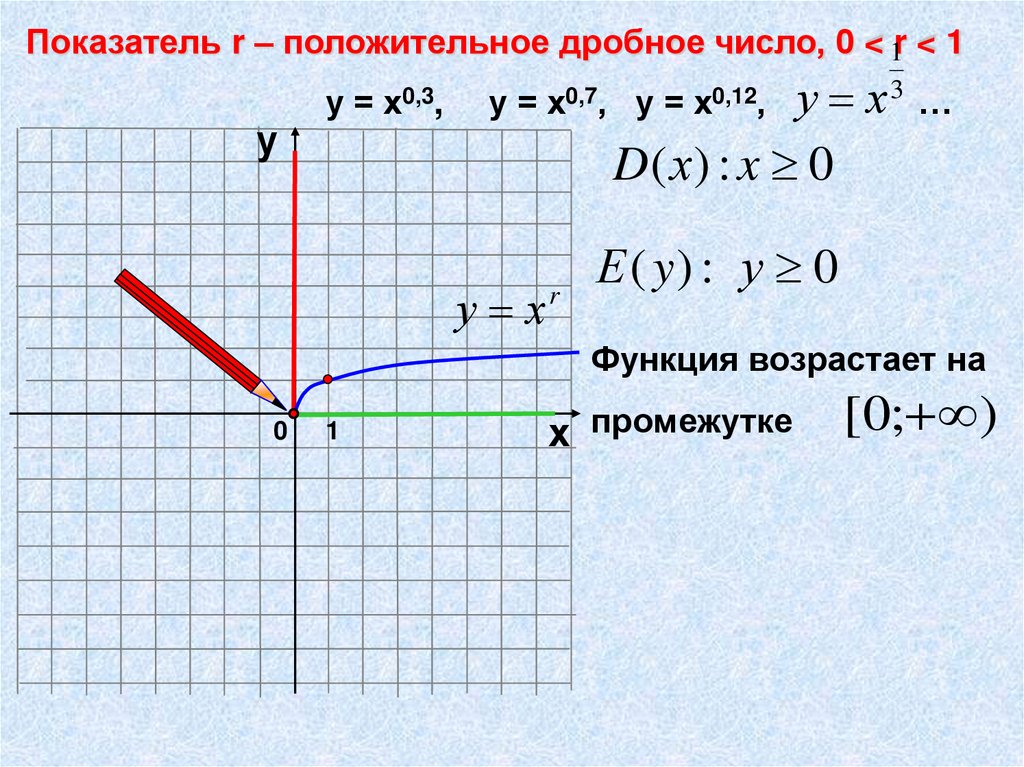
Показатель r – положительное дробное число, 0 < 1r < 1
у
у = х0,3,
у = х0,7, у = х0,12,
у х3 …
D( х) : x 0
у х
r
Е ( y) : у 0
Функция возрастает на
0
1
х промежутке
[0; )

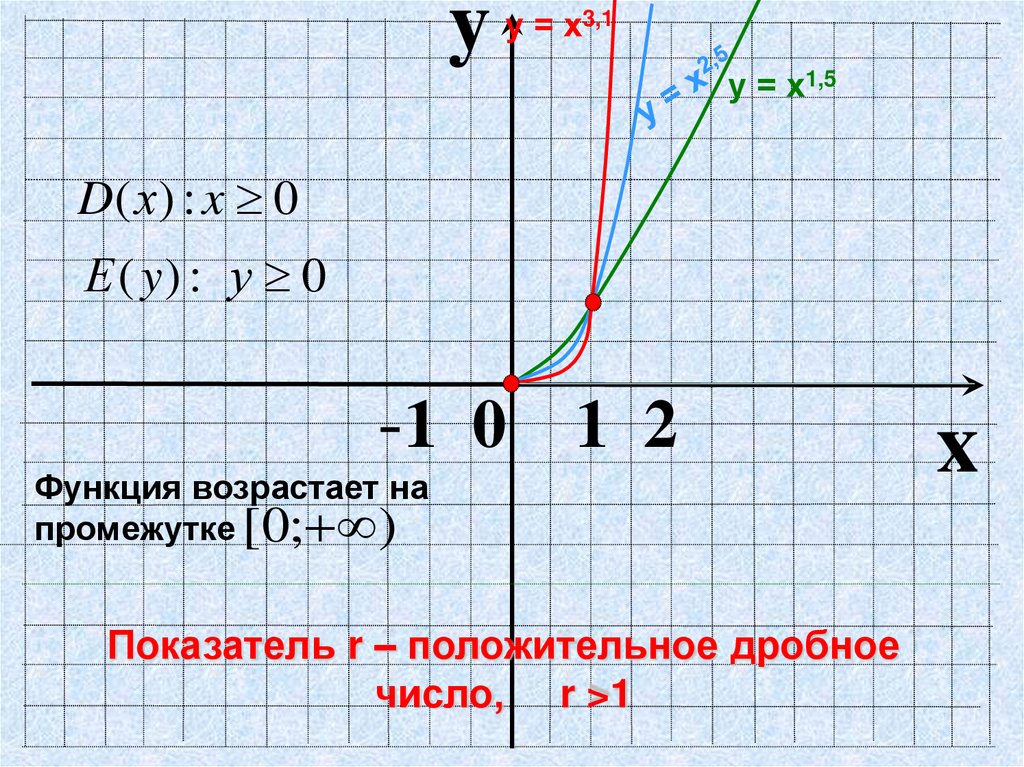
8.

y
у = х3,1
у = х1,5
D( х) : x 0
Е ( y) : у 0
-1 0 1 2
Функция возрастает на
промежутке [0; )
Показатель r – положительное дробное
число, r >1
x

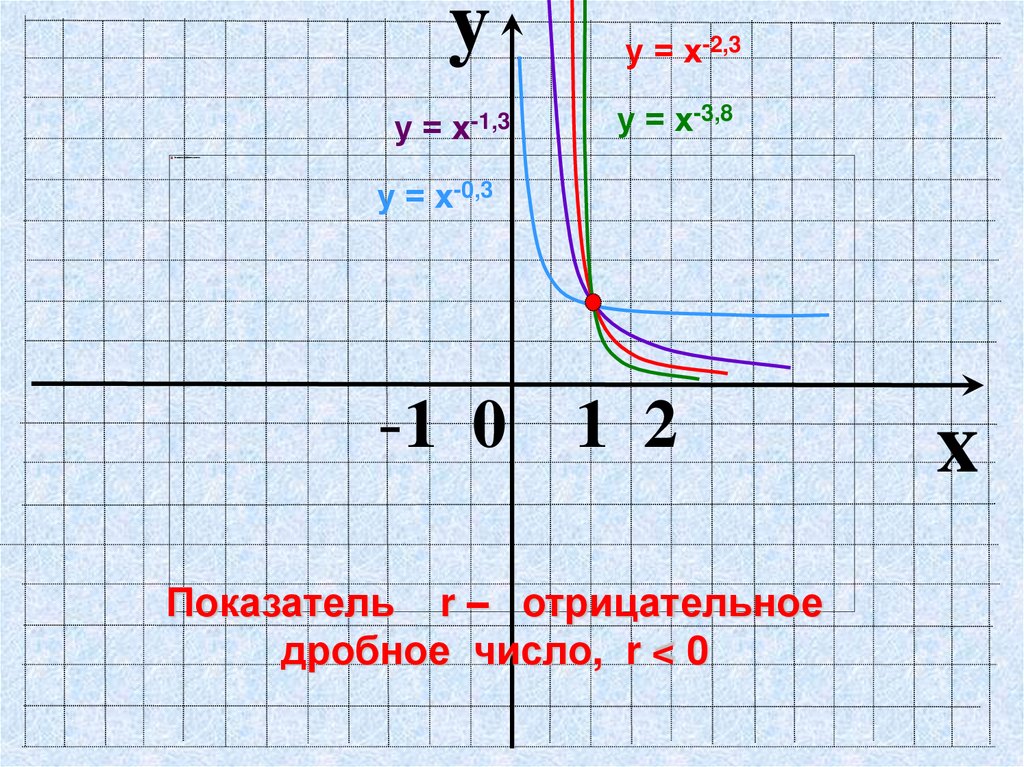
9.

y
у = х-2,3
у = х-1,3
у = х-3,8
у = х-0,3
-1 0 1 2
Показатель r – отрицательное
дробное число, r < 0
x

10.

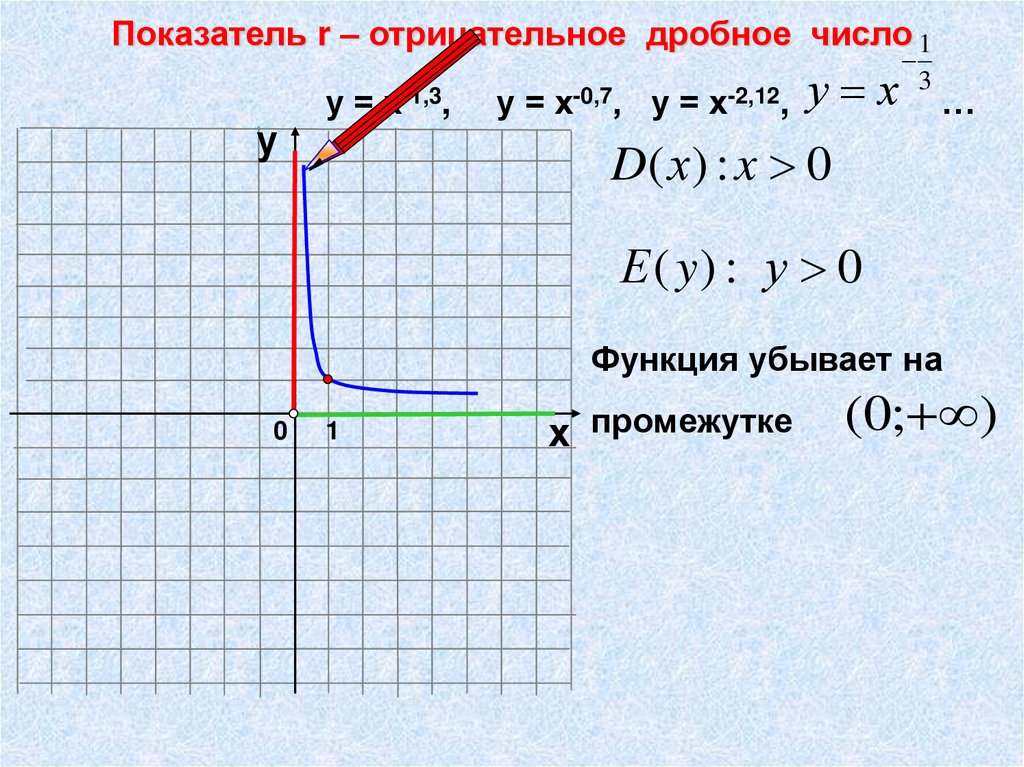
Показатель r – отрицательное дробное число 1
у
у = х-1,3,
у = х-0,7,
у = х-2,12,
у х 3…
D( х) : x 0
Е ( y) : у 0
Функция убывает на
0
1
х промежутке
(0; )

11.

12.

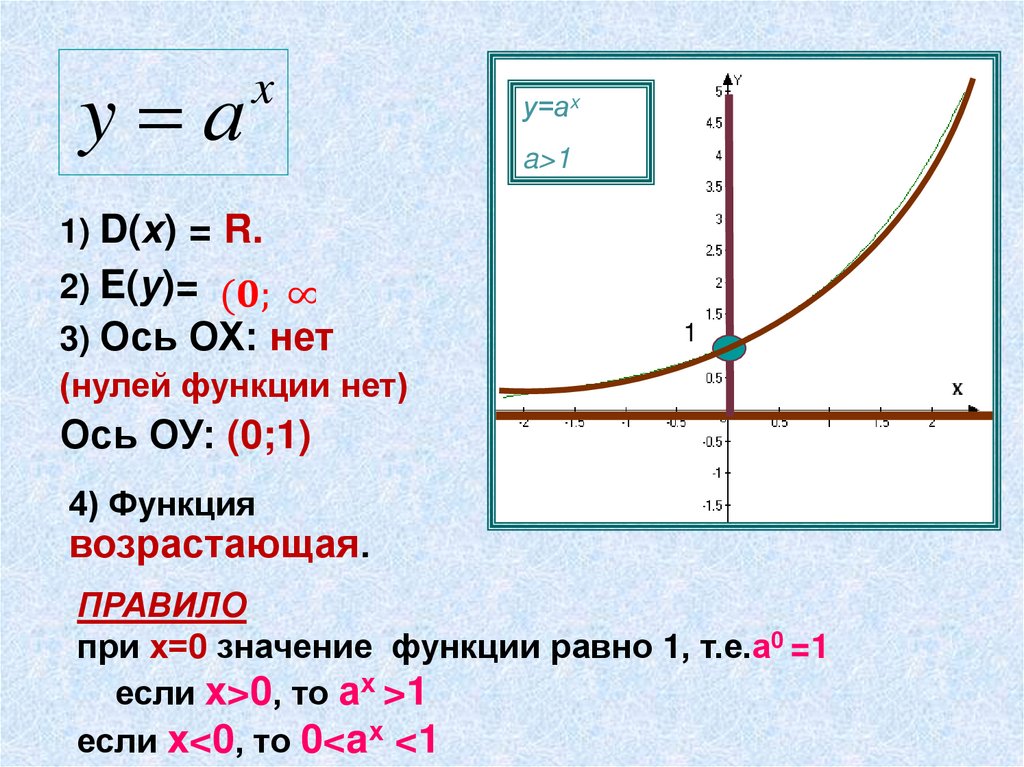
y а
x
у=аx
a>1
1) D(х) = R.
2) E(у)=
3) Ось ОХ: нет
(нулей функции нет)
1
Ось ОУ: (0;1)
4) Функция
возрастающая.
ПРАВИЛО
при х=0 значение функции равно 1, т.е.а0 =1
если х>0, то ах >1
если х<0, то 0<aх <1

13.

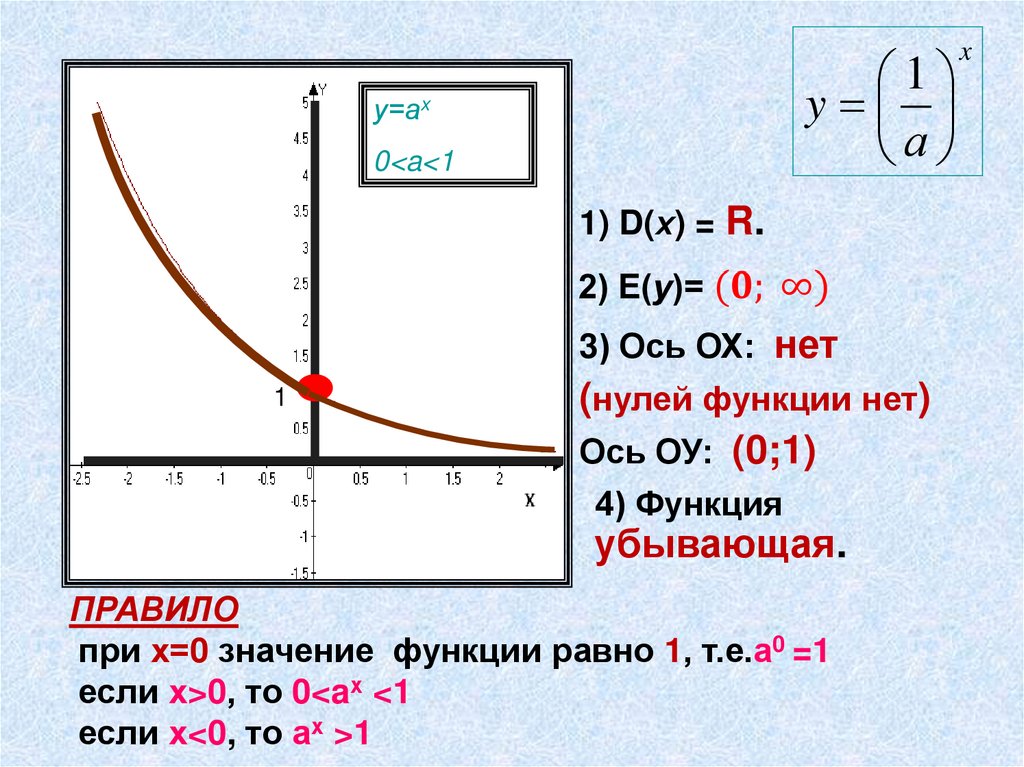
1
y
а
у=аx
0<a<1
1) D(х) = R.
3) Ось ОХ: нет
1
(нулей функции нет)
Ось ОУ: (0;1)
4) Функция
убывающая.
ПРАВИЛО
при х=0 значение функции равно 1, т.е.а0 =1
если х>0, то 0<aх <1
если х<0, то ах >1
x

14.

Функция y = log x,
её свойства и график.
a
14

15.

Свойства функции у = loga x, a > 1.
1) D(f) = (0, + ∞);
2) E(f) = (- ∞, + ∞);
3) не является ни чётной,
0
ни нечётной;
4) возрастает на (0, + ∞);
5)Экстремальных точек -нет
6) непрерывна;
7) с ОХ (1;0)
выпукла вверх
у
y log a x
х
15

16.

Свойства функции у = loga x, 0 < a < 1.
1) D(f) = (0, + ∞);
2) E(f) = (- ∞, + ∞);
3) не является ни чётной,
0
ни нечётной;
4) убывает на (0, + ∞);
5) Экстремальных точек -нет
6) непрерывна;
7) с ОХ (1;0)
у
y log a x
х
выпукла вниз
16

17. Тригонометрические функции числового аргумента.

y = sin x
y = cos x

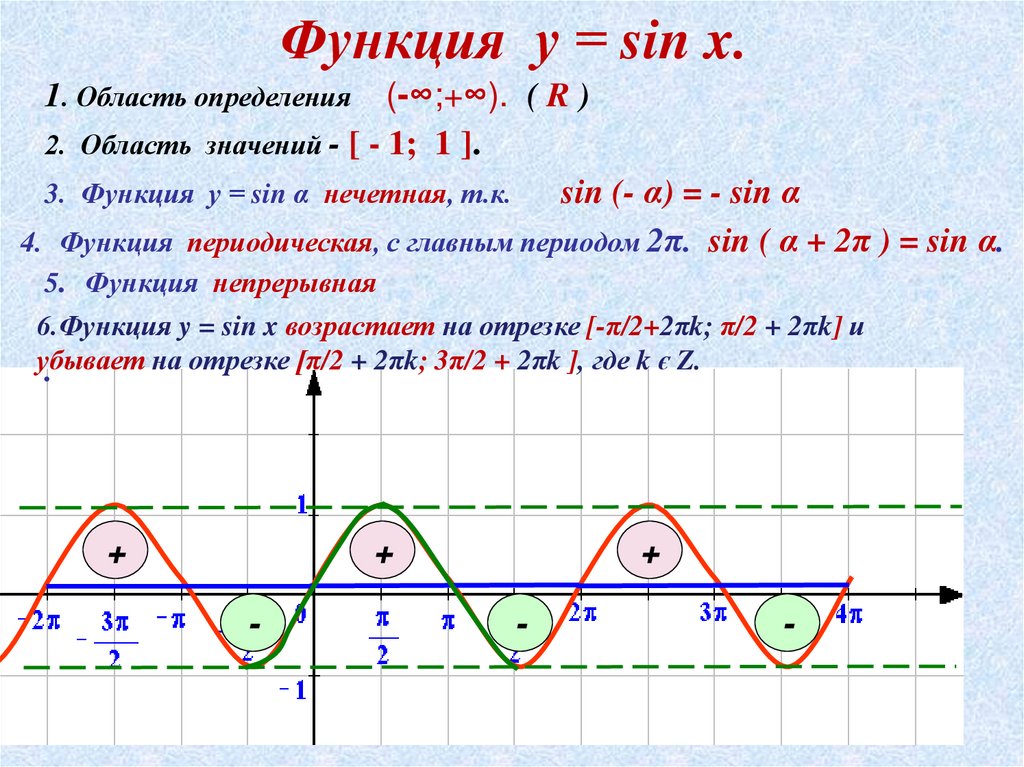
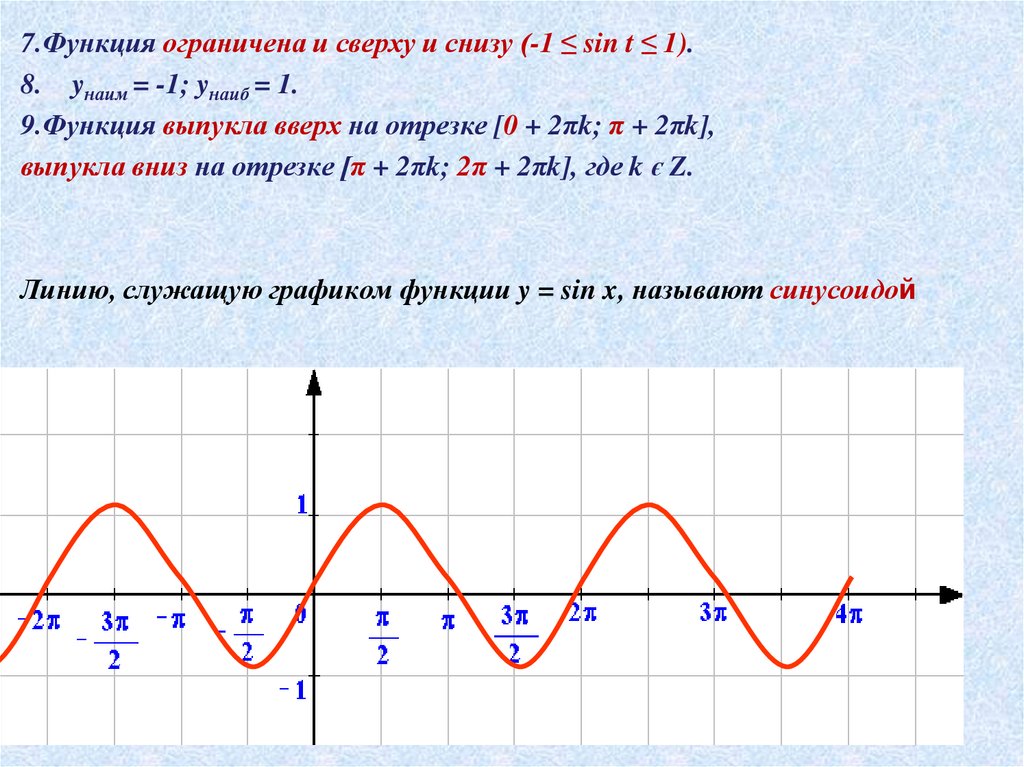
18. Функция у = sin x.

1. Область определения (-∞;+∞). ( R )
2. Область значений - [ - 1; 1 ].
3. Функция у = sin α нечетная, т.к.
sin (- α) = - sin α
4. Функция периодическая, с главным периодом 2π. sin ( α + 2π ) = sin α.
5. Функция непрерывная
6.Функция y = sin x возрастает на отрезке [-π/2+2πk; π/2 + 2πk] и
убывает
на отрезке [π/2 + 2πk; 3π/2 + 2πk ], где k є Z.
.
+
+
-
+
-
-

19.

7.Функция ограничена и сверху и снизу (-1 ≤ sin t ≤ 1).
8. yнаим = -1; yнаиб = 1.
9.Функция выпукла вверх на отрезке [0 + 2πk; π + 2πk],
выпукла вниз на отрезке [π + 2πk; 2π + 2πk], где k є Z.
Линию, служащую графиком функции y = sin x, называют синусоидой

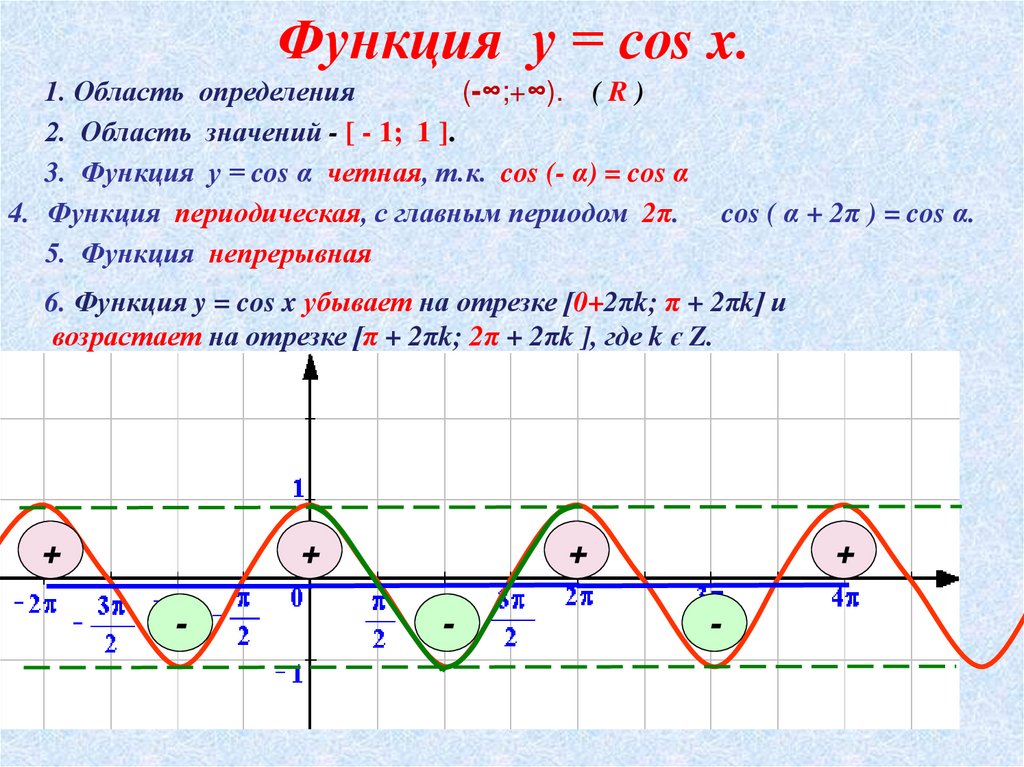
20. Функция у = соs x.

1. Область определения
(-∞;+∞). ( R )
2. Область значений - [ - 1; 1 ].
3. Функция у = cos α четная, т.к. cos (- α) = cos α
4. Функция периодическая, с главным периодом 2π.
5. Функция непрерывная
cos ( α + 2π ) = cos α.
6. Функция y = cos x убывает на отрезке [0+2πk; π + 2πk] и
возрастает на отрезке [π + 2πk; 2π + 2πk ], где k є Z.
+
+
-
+
-
+
-

21.

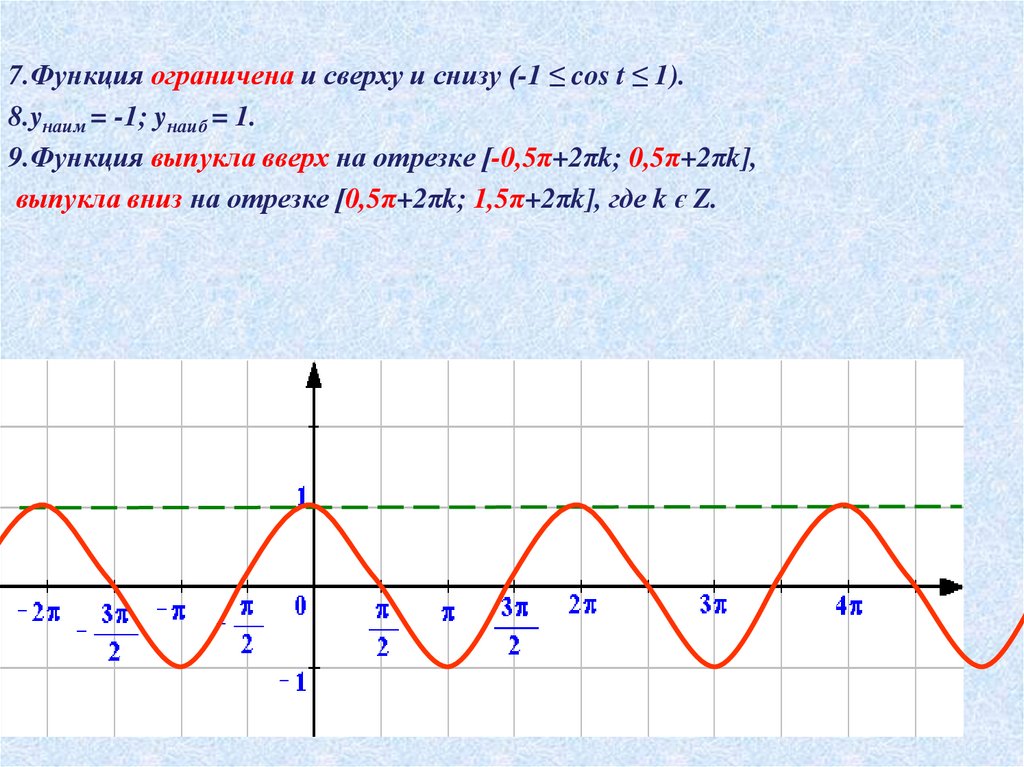
7.Функция ограничена и сверху и снизу (-1 ≤ cos t ≤ 1).
8.yнаим = -1; yнаиб = 1.
9.Функция выпукла вверх на отрезке [-0,5π+2πk; 0,5π+2πk],
выпукла вниз на отрезке [0,5π+2πk; 1,5π+2πk], где k є Z.

22.

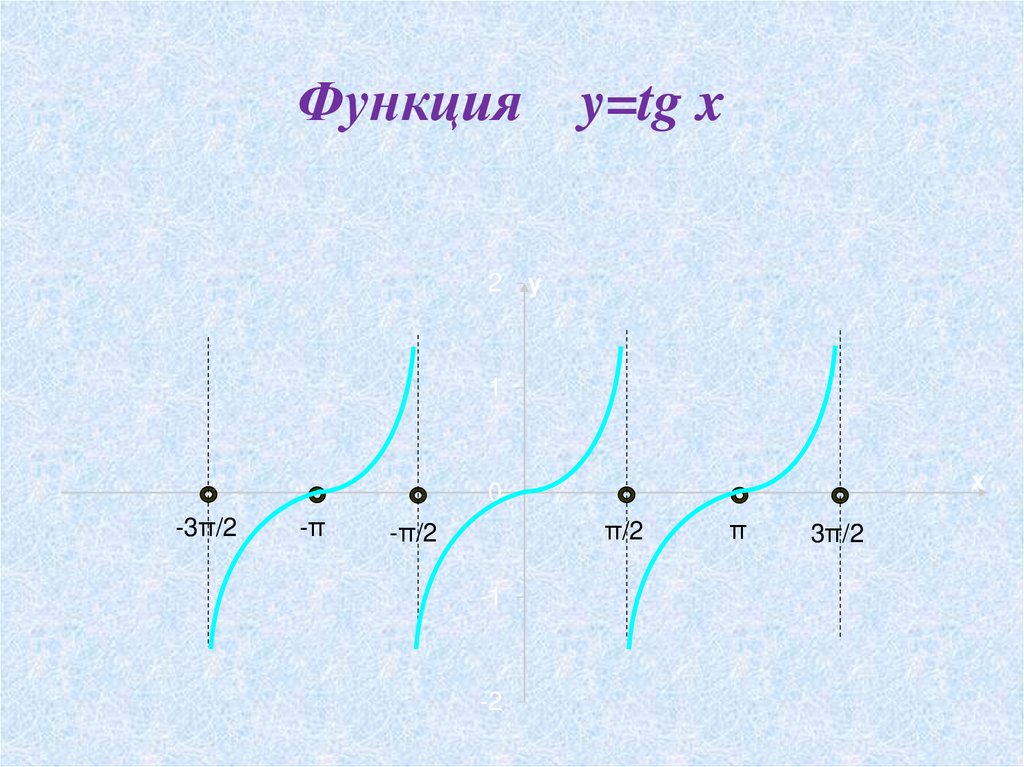
Функция
y=tg x
2 y
1
x
0
-3π/2
-π
π/2
-π/2
-1
-2
π
3π/2

23.

Функция
1. Область
y = tg x
определения (-π/2;+ π /2).
2. Область значений (-∞;+∞).
3. y = tg x – нечётная функция. tg (- α) = - tg α
4. Функция y = tg x периодическая, ее период равен π.
5. y = tg x – непрерывная функция.
6. Функция y = tg x возрастает на отрезке
(-π/2 + πk; π/2 + πk ), где k є Z.
7. Функция знакопеременная
8. наибольшего и наименьшего значения функции
нет.
9. Есть вертикальные асимптоты.

24.

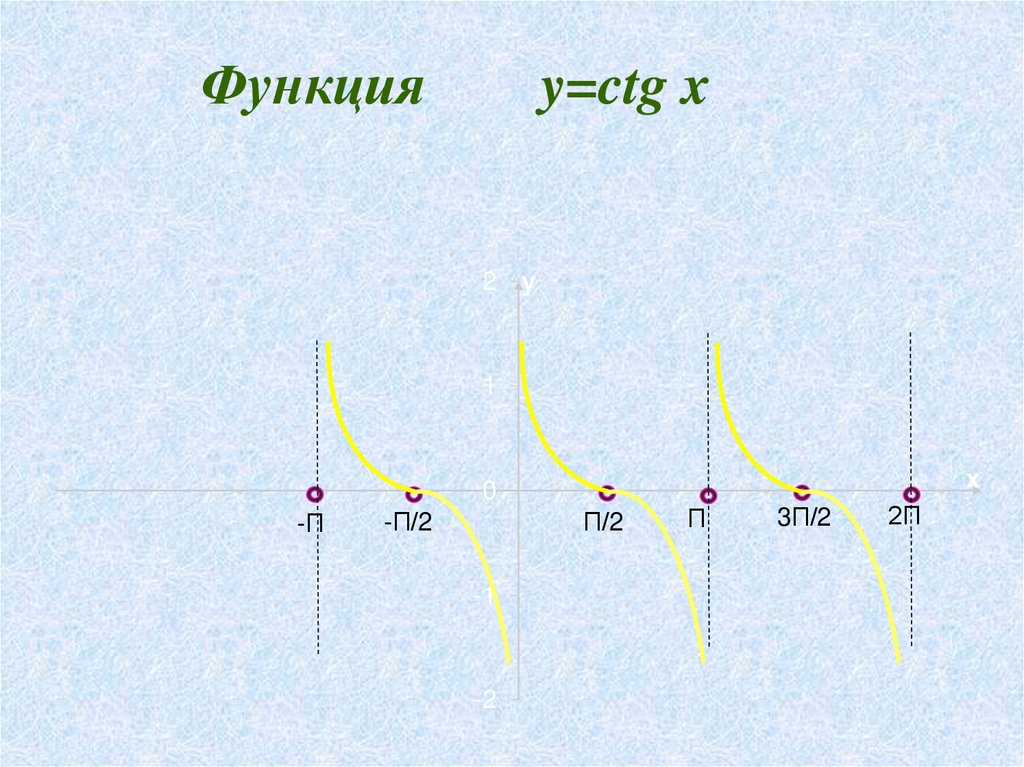
Функция
y=ctg x
2 y
1
x
0
-П
П/2
-П/2
-1
-2
П
3П/2
2П

25.

Функция
y=ctg x
1.Область определения (0; π ).
2.Область значений (-∞;+∞).
3.y = ctg x – нечётная функция. ctg (- α) = - ctg α
4.Функция y = ctg x периодическая, ее период равен
π.
5.y = ctg x – непрерывная функция.
6.Функция y = ctg x убывает на отрезке
(0+πk;
π + πk ), где k є Z.
7.Функция знакопеременная
8.наибольшего и наименьшего значения функции
нет.
9.Есть вертикальные асимптоты.