Презентация к уроку геометрии _Правильные многоугольники_ вычисление их элементов. Окружность_ описанная около правильного многоугольник

1. Правильные многоугольники, вычисление их элементов. Окружность, описанная около правильного многоугольника. Окружность,

вписанная в правильный многоугольник.

2. Правильный многоугольник

• Правильным многоугольником называется выпуклый многоугольник, у
которого все углы равны и все стороны равны.
• Сумма градусных мер углов любого выпуклого n-угольника равна
180°(n - 2).
• Градусную меру каждого его угла можно найти по формуле:

3. Определения

4. Теорема об окружности, описанной около правильного многоугольника.

• Около любого правильного многоугольника можно
описать окружность, и притом только одну.

5. Теорема об окружности, вписанной в правильный многоугольник.

• В любой правильный многоугольник
можно вписать окружность, и притом
только одну.

6. Следствия

• следствие 1: окружность, вписанная в правильный многоугольник, касается сторон
многоугольника в их серединах.
• следствие 2: центр окружности, описанной около правильного многоугольника,
совпадает с центром окружности, вписанной в тот же многоугольник. Эта точка
называется центром правильного многоугольника.

7.

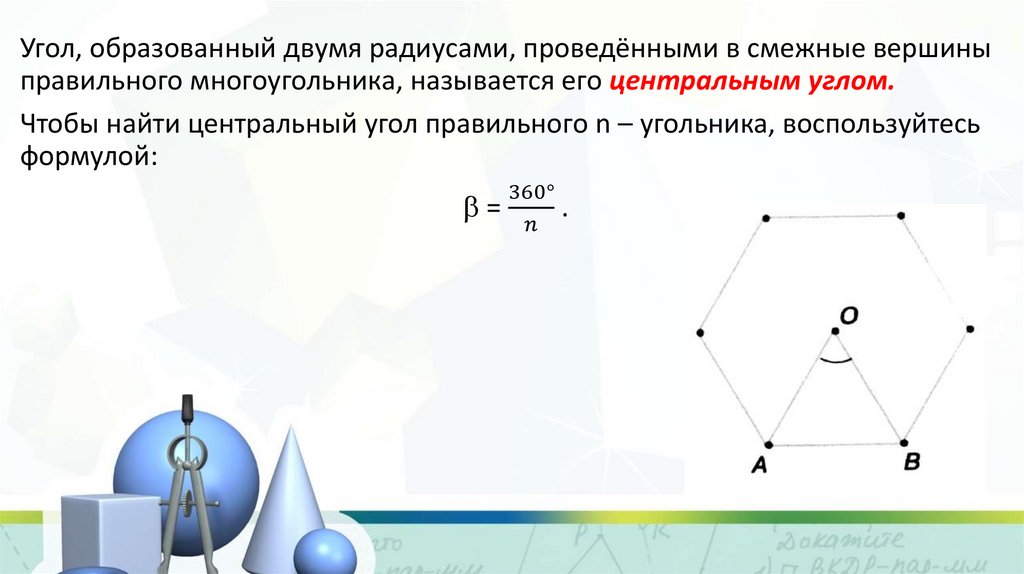
Угол, образованный двумя радиусами, проведёнными в смежные вершины
правильного многоугольника, называется его центральным углом.
Чтобы найти центральный угол правильного n – угольника, воспользуйтесь
формулой:
360°
=
.