Лекция 2 новая (1)

1.

Лекция №2
ПОНЯТИЕ: ВИДЫ И ЛОГИЧЕСКИЕ
ОПЕРАЦИИ С НИМ

2.

Лекция №2
1. Понятие как форма мышления
2. Виды понятий
3. Отношения между понятиями
4. Логические операции с понятием

3.

Лекция 2. Понятие: виды и логические операции с ним
Вопрос 1.
Понятие как форма мышления

4.

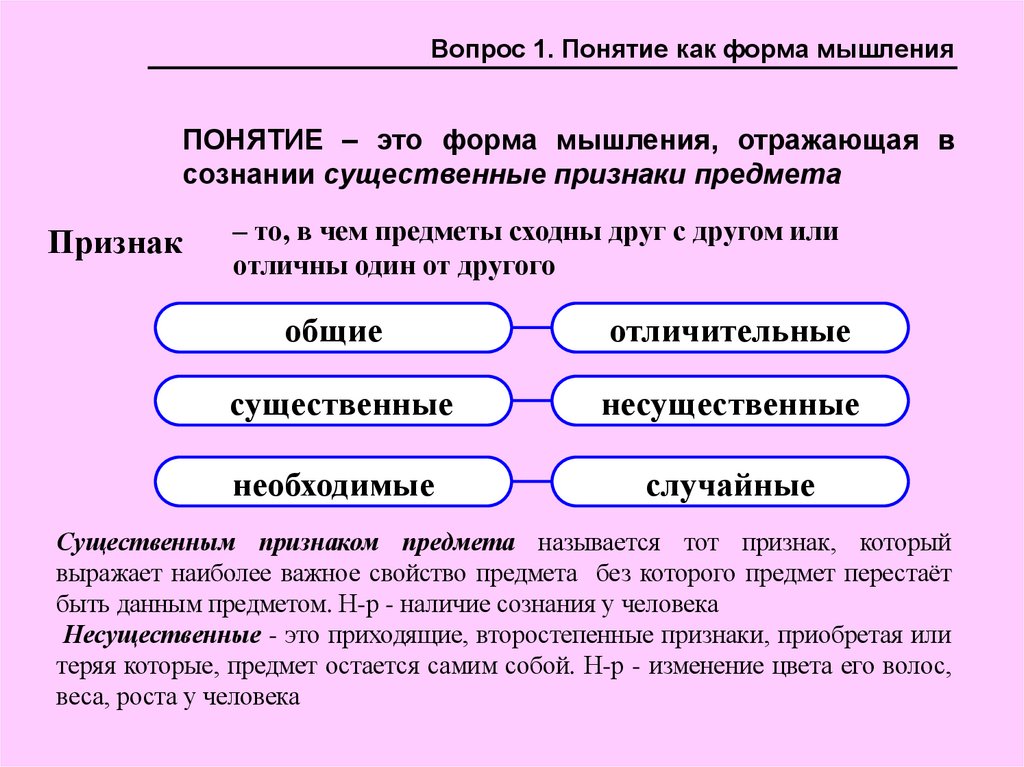
Вопрос 1. Понятие как форма мышления
ПОНЯТИЕ – это форма мышления, отражающая в
сознании существенные признаки предмета
Признак
– то, в чем предметы сходны друг с другом или
отличны один от другого
общие
отличительные
существенные
несущественные
необходимые
случайные
Существенным признаком предмета называется тот признак, который
выражает наиболее важное свойство предмета без которого предмет перестаёт
быть данным предметом. Н-р - наличие сознания у человека
Несущественные - это приходящие, второстепенные признаки, приобретая или
теряя которые, предмет остается самим собой. Н-р - изменение цвета его волос,
веса, роста у человека

5.

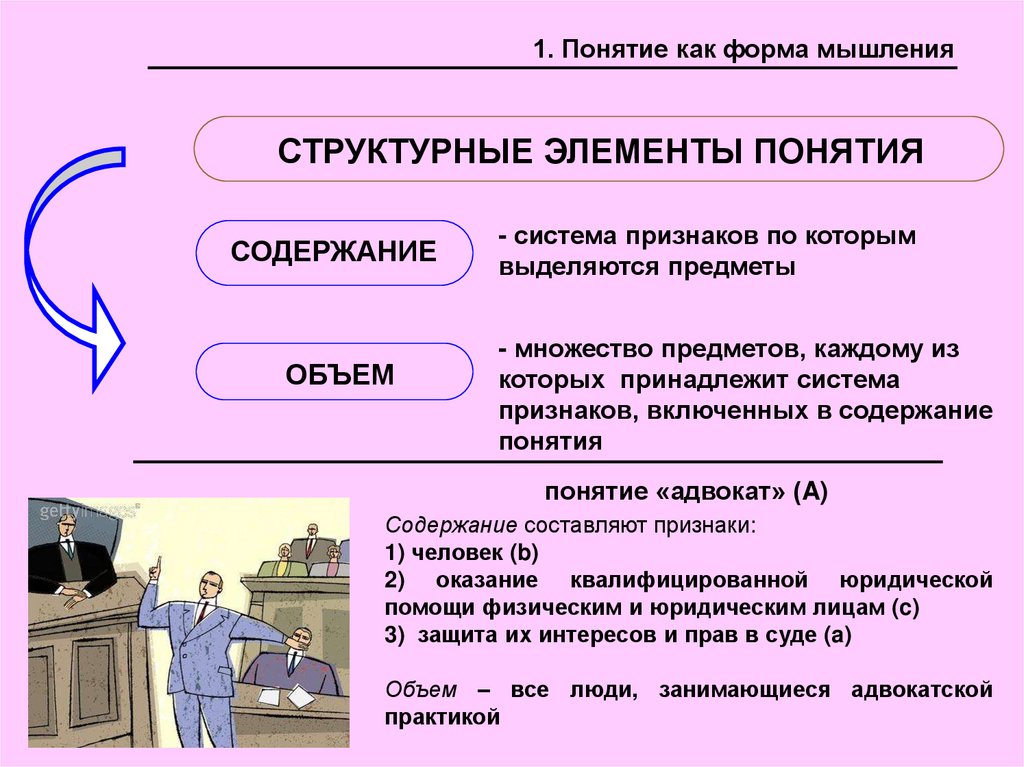
1. Понятие как форма мышления
СТРУКТУРНЫЕ ЭЛЕМЕНТЫ ПОНЯТИЯ
СОДЕРЖАНИЕ
ОБЪЕМ
- система признаков по которым
выделяются предметы
- множество предметов, каждому из
которых принадлежит система
признаков, включенных в содержание
понятия
понятие «адвокат» (A)
Содержание составляют признаки:
1) человек (b)
2) оказание квалифицированной юридической
помощи физическим и юридическим лицам (c)
3) защита их интересов и прав в суде (a)
Объем – все люди, занимающиеся адвокатской
практикой

6.

НЕМНОГО ИСТОРИИ…
Леонард Эйлер (1707-1783) –
швейцарский математик, долго
работавший в Петербургской
Академии наук. В «Письмах к
немецкой принцессе» (1761-1768)
рассказывает о своем методе
Эрнест Шредер (1841-1902) –
немецкий математик, широко
использующий метод кругов Эйлера в
своей книге «Алгебра логики»
Джон Венн (1834-1923)
английский
логик.
В
книге
«Символическая
логика»
(1881,
Лондон) графический метод изложен с
наибольшей полнотой.
В честь Венна вместо кругов Эйлера
соответствующие рисунки называют
иногда
диаграммами
Венна;
в
некоторых книгах их называют также
диаграммами (или кругами) ЭйлераВенна.
Готфрид Вильгельм Лейбниц
(1646-1716) –
первый использовал для решения
задач изображения кругов
Бернард Больцано (1781-1848)
чешский математик, в отличие от
Эйлера рисовал не круговые, а
прямоугольные схемы

7.

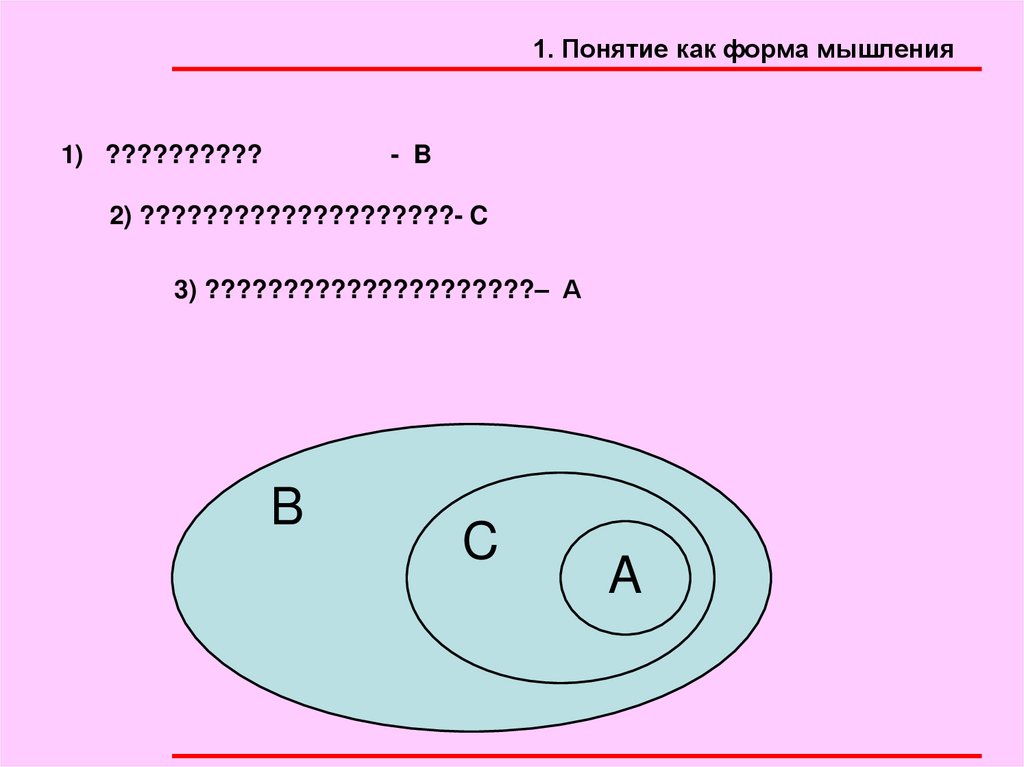
1. Понятие как форма мышления
1) ??????????
- B
2) ????????????????????- C
3) ?????????????????????– А
B
C
A

8.

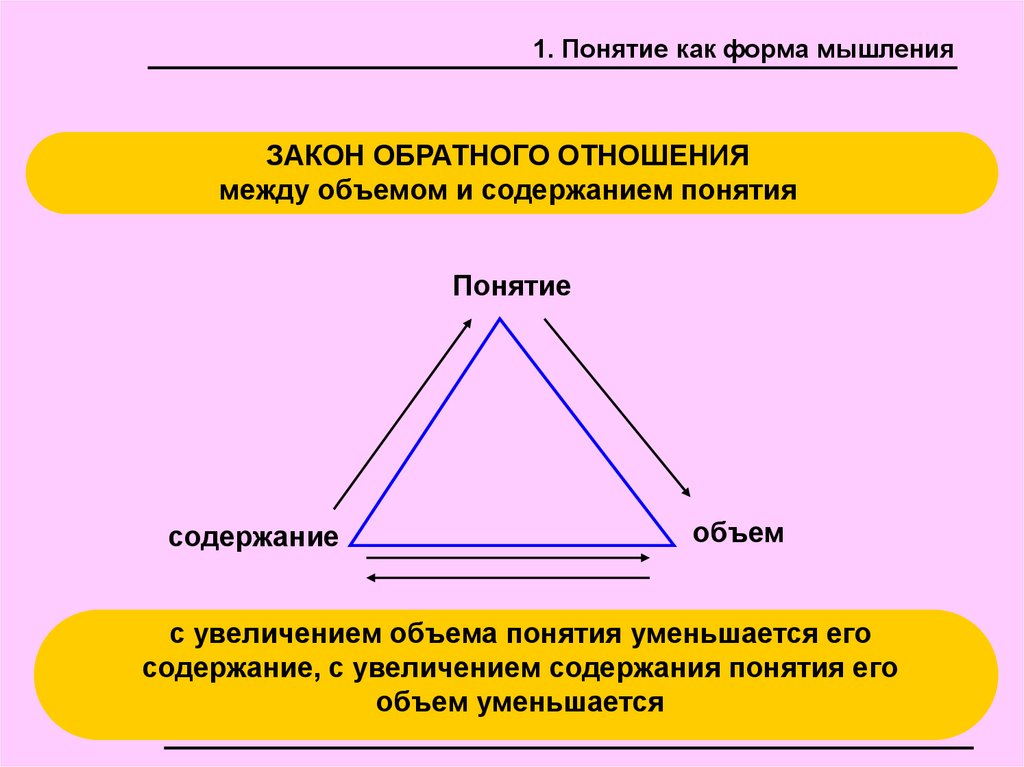
1. Понятие как форма мышления
ЗАКОН ОБРАТНОГО ОТНОШЕНИЯ
между объемом и содержанием понятия
Понятие
содержание
объем
с увеличением объема понятия уменьшается его
содержание, с увеличением содержания понятия его
объем уменьшается

9.

Лекция 2. Понятие: виды и логические операции с ним
Вопрос 2.
Виды понятий

10.

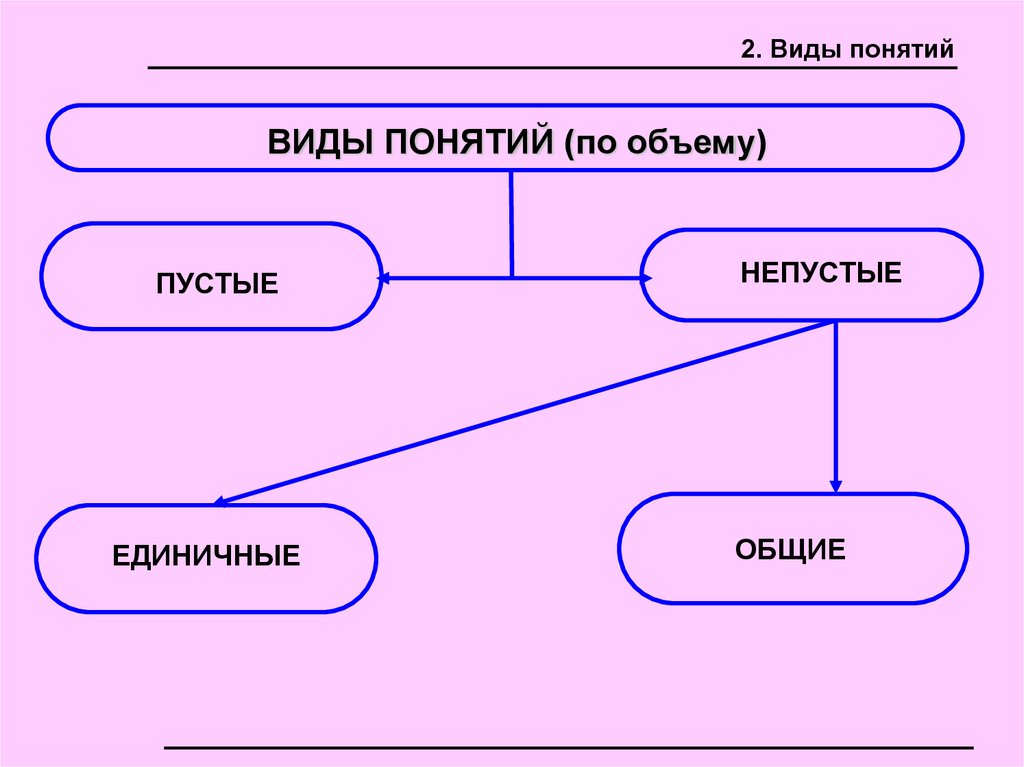
2. Виды понятий
ВИДЫ ПОНЯТИЙ (по объему)
ПУСТЫЕ
ЕДИНИЧНЫЕ
НЕПУСТЫЕ
ОБЩИЕ

11.

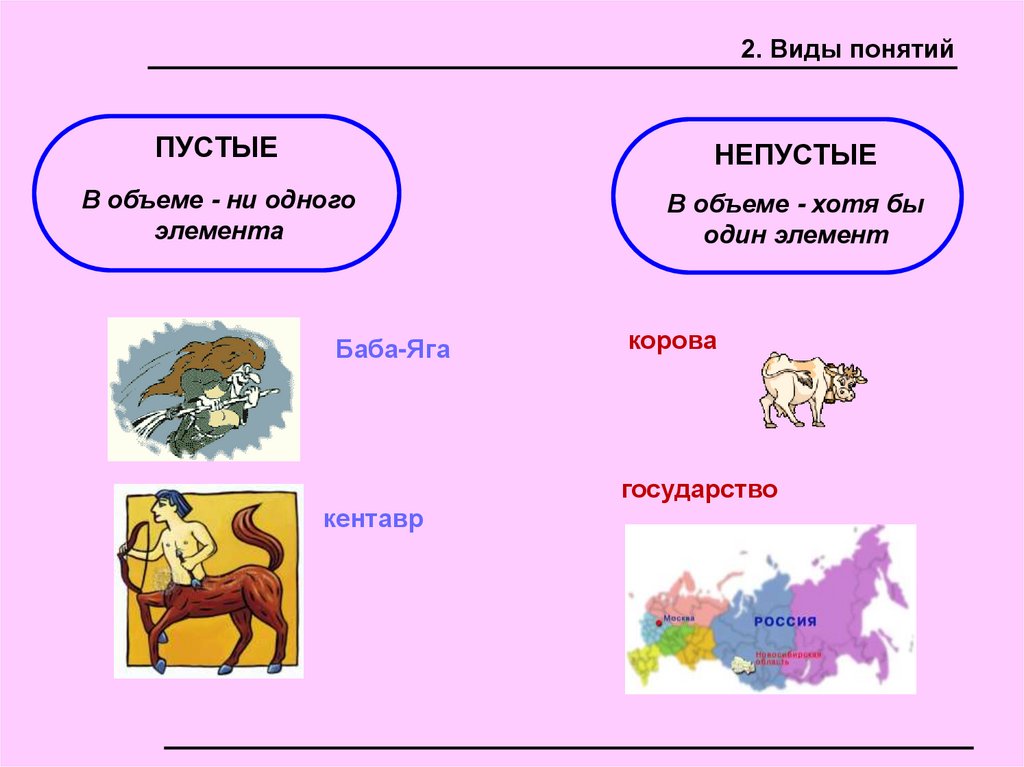
2. Виды понятий
ПУСТЫЕ
НЕПУСТЫЕ
В объеме - ни одного
элемента
В объеме - хотя бы
один элемент
Баба-Яга
корова
государство
кентавр

12.

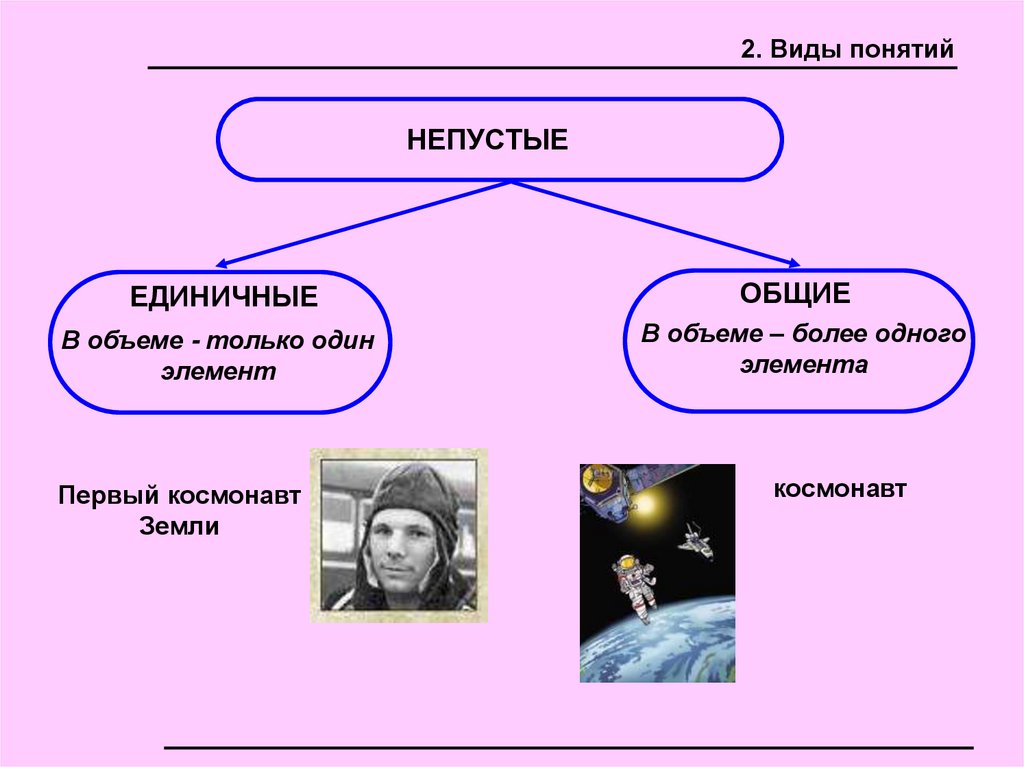
2. Виды понятий
НЕПУСТЫЕ
ЕДИНИЧНЫЕ
ОБЩИЕ
В объеме - только один
элемент
В объеме – более одного
элемента
Первый космонавт
Земли
космонавт

13.

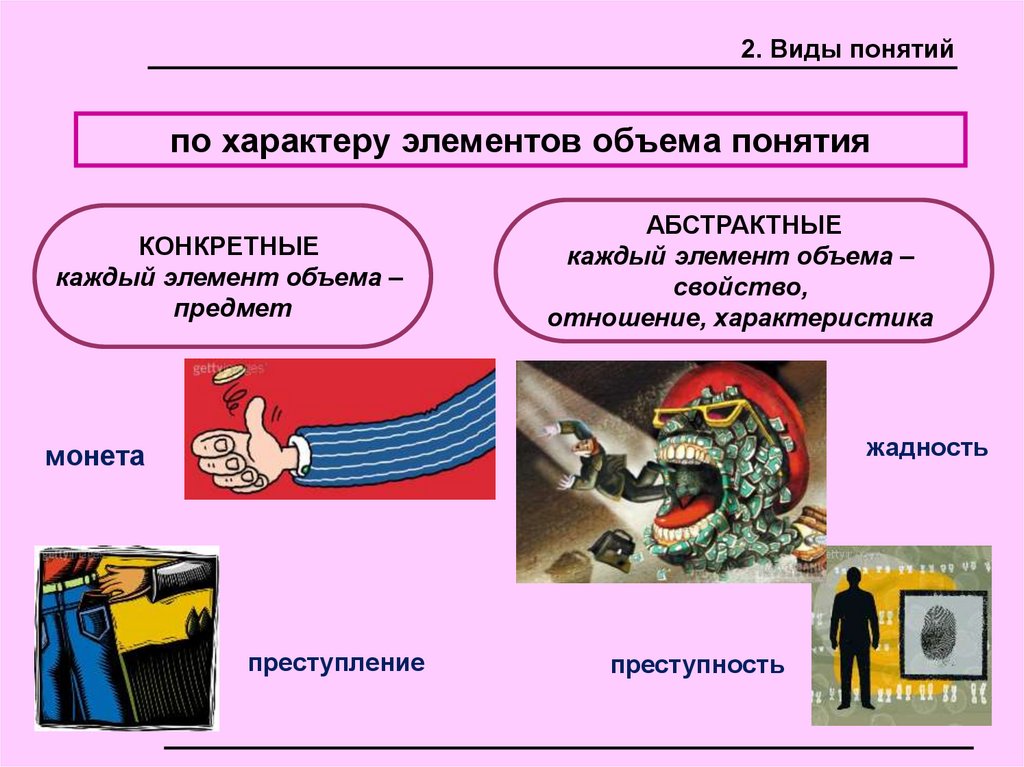
2. Виды понятий
по характеру элементов объема понятия
КОНКРЕТНЫЕ
каждый элемент объема –
предмет
АБСТРАКТНЫЕ
каждый элемент объема –
свойство,
отношение, характеристика
жадность
монета
преступление
преступность

14.

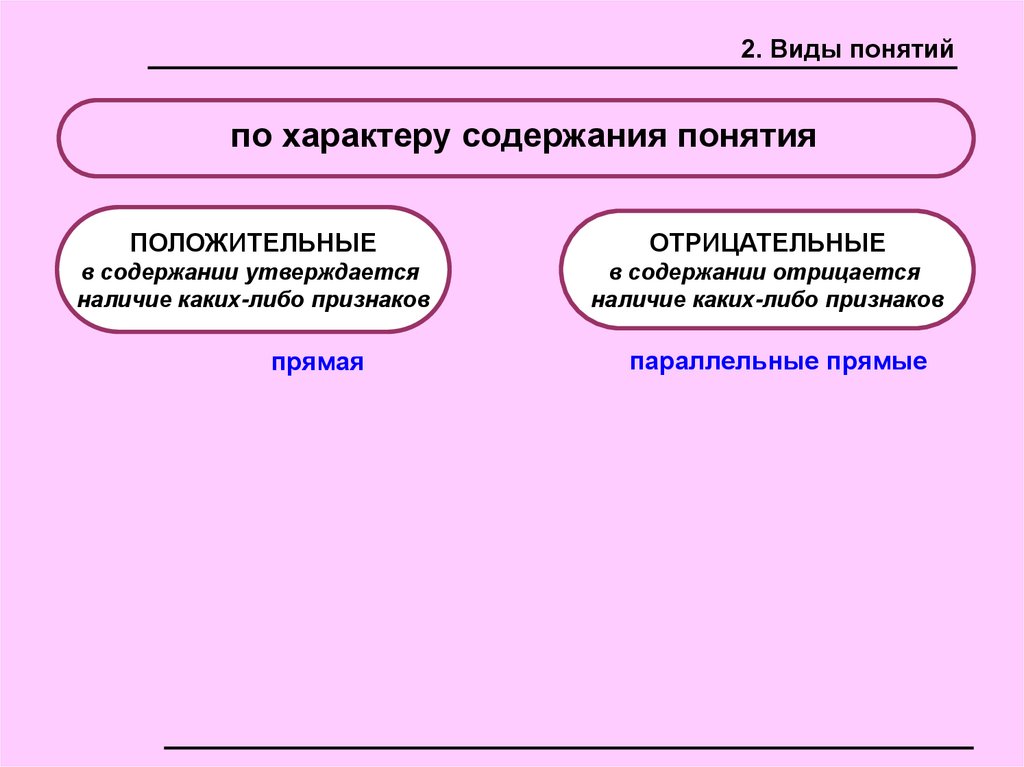
2. Виды понятий
по характеру содержания понятия
ПОЛОЖИТЕЛЬНЫЕ
ОТРИЦАТЕЛЬНЫЕ
в содержании утверждается
наличие каких-либо признаков
в содержании отрицается
наличие каких-либо признаков
прямая
параллельные прямые

15.

Лекция 2. Понятие: виды и логические операции с ним
Вопрос 3.
Отношения между понятиями

16.

3. Отношения между понятиями
ОТНОШЕНИЯ МЕЖДУ ПОНЯТИЯМИ
НЕСРАВНИМОСТЬ
СРАВНИМОСТЬ
в содержании понятий
есть хотя бы один
общий признак
«автобус» - «автомобиль»
по содержанию
в содержании понятий
нет ни одного общего
признака
«университет» - «студент»

17.

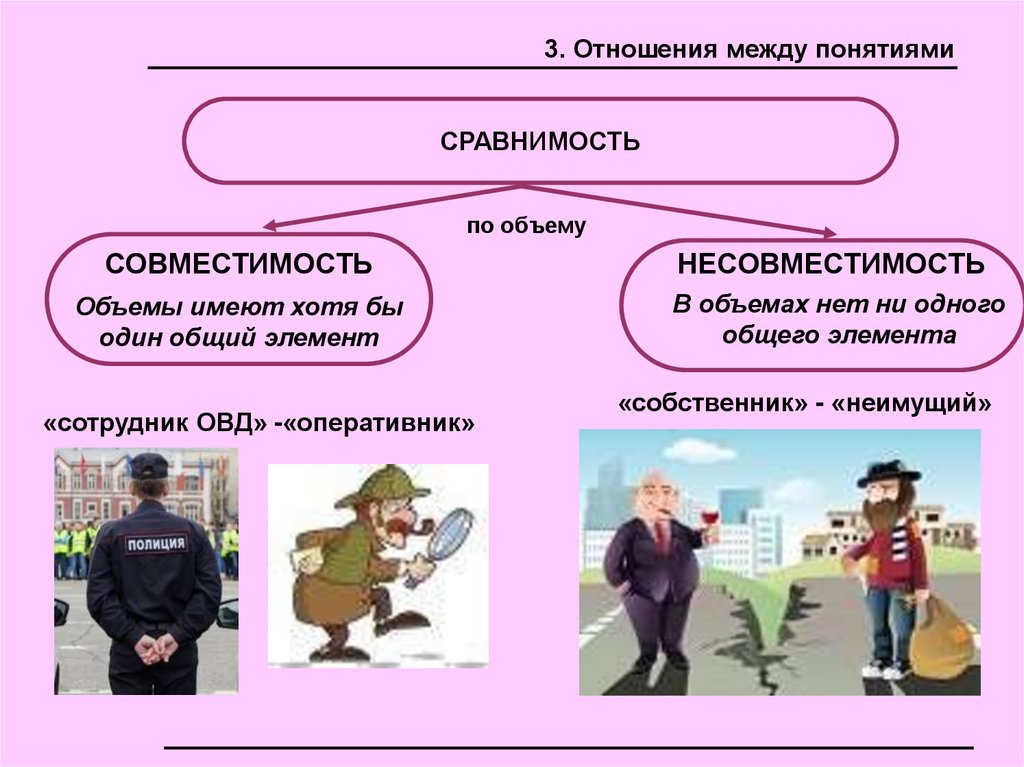
3. Отношения между понятиями
СРАВНИМОСТЬ
по объему
СОВМЕСТИМОСТЬ
НЕСОВМЕСТИМОСТЬ
Объемы имеют хотя бы
один общий элемент
В объемах нет ни одного
общего элемента
«сотрудник ОВД» -«оперативник»
«собственник» - «неимущий»

18.

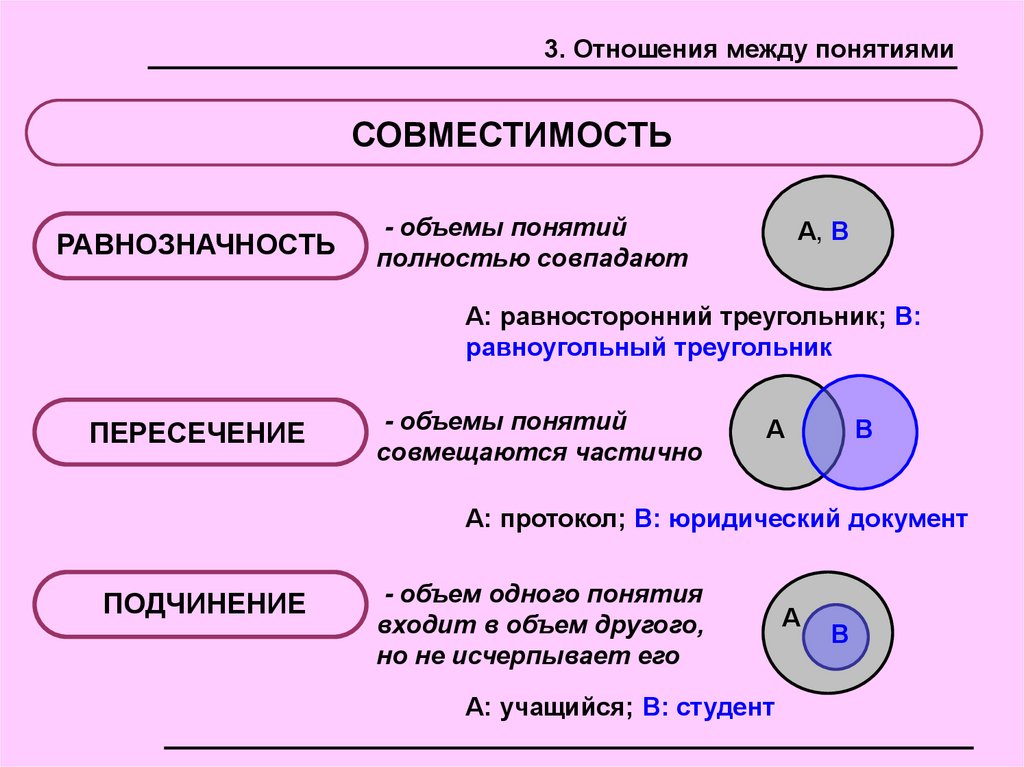
3. Отношения между понятиями
СОВМЕСТИМОСТЬ
РАВНОЗНАЧНОСТЬ
- объемы понятий
полностью совпадают
А, В
А: равносторонний треугольник; В:
равноугольный треугольник
ПЕРЕСЕЧЕНИЕ
- объемы понятий
совмещаются частично
А
В
А: протокол; В: юридический документ
ПОДЧИНЕНИЕ
- объем одного понятия
входит в объем другого,
но не исчерпывает его
А: учащийся; В: студент
А
В

19.

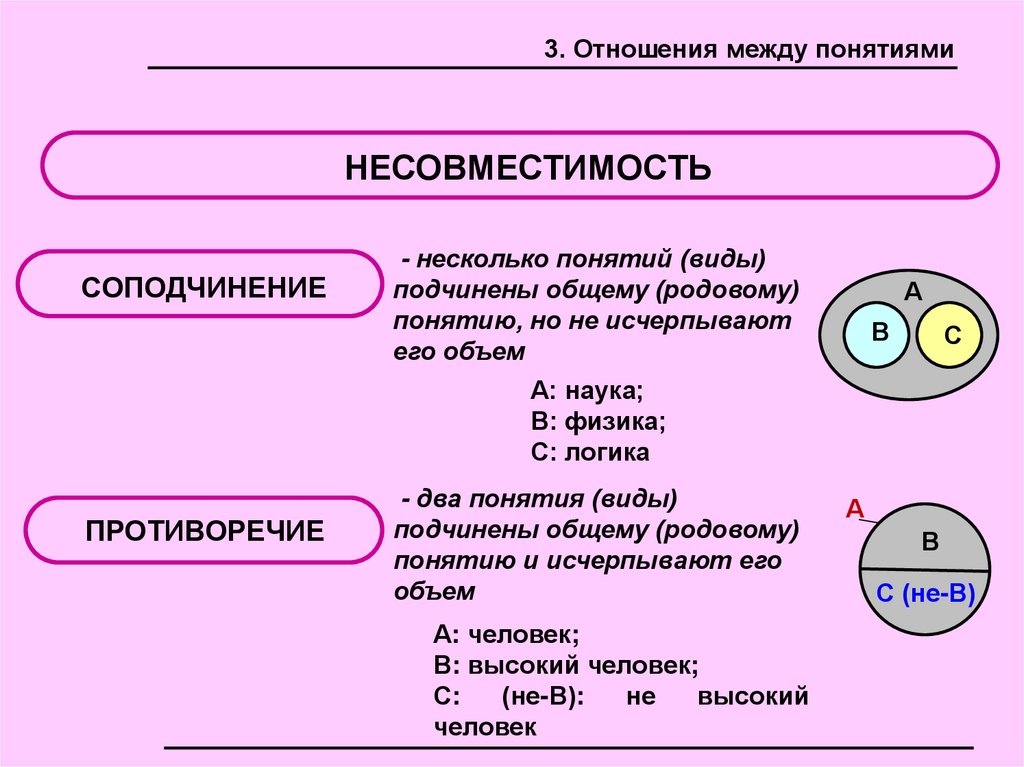
3. Отношения между понятиями
НЕСОВМЕСТИМОСТЬ
СОПОДЧИНЕНИЕ
- несколько понятий (виды)
подчинены общему (родовому)
понятию, но не исчерпывают
его объем
А
В
С
А: наука;
В: физика;
С: логика
ПРОТИВОРЕЧИЕ
- два понятия (виды)
подчинены общему (родовому)
понятию и исчерпывают его
объем
А: человек;
В: высокий человек;
С:
(не-В):
не
высокий
человек
А
В
С (не-В)

20.

Лекция 2. Понятие: виды и логические операции с ним
Практикум
Работа 1. Задание 1.

21.

Работа 1. Понятие: отношения между понятиями и
логические операции с понятием
Задание 1. Подберите понятия, находящиеся в логических отношениях с
данным понятием.
Отношение подчинения
Если понятие А – «депутат», то родовое (подчиняющее) понятие В
В
А
– «человек».
Проверяем образовавшиеся отношения между понятиями А и В по
следующей схеме: «Всякий элемент объема понятия А является
элементом объема понятия В, но не наоборот».
«Всякий «депутат» есть «человек», но не наоборот».
Полученное высказывание является истинным, следовательно,
понятия подобраны правильно.
А
В1
Если понятие А – «депутат», то видовое (подчиненное) понятие
В1 – «депутат Государственной Думы РФ».
Проверяем образовавшиеся отношения между понятиями А и В
по следующей схеме: «Всякий элемент объема понятия В1
является элементом объема понятия А, но не наоборот».
«Всякий «депутат Государственной Думы РФ» есть «депутат»,
но не наоборот».
Полученное высказывание является истинным, следовательно,
понятия подобраны правильно.

22.

В
В2
А
Отношение перекрещивания
Чтобы правильно подобрать перекрещивающееся понятие В2,
необходимо работать в объеме родового понятия В «человек»,
прибавляя в его содержание новый отличительный признак.
Понятие В2 «высокий человек», будет иметь некоторые общие
элементы объема с понятием А «депутат», и одновременно
подчиняться понятию В «человек».
Проверяем образовавшиеся отношения между понятиями А и В2 по
следующей схеме: «Некоторые элементы объема А (но не все)
являются элементами объема В2, и наоборот»
«Некоторые «депутаты» (но не все) являются «высокими людьми»,
и наоборот».
Полученное высказывание является истинным, следовательно,
понятия подобраны правильно.

23.

В
В3
А
Отношение соподчинения
Чтобы правильно подобрать соподчиненное понятие В3,
необходимо работать в объеме родового понятия В «человек»,
добавляя к его содержанию отличительный признак, которого не
может быть у понятия А.
Понятие В3 «министр» не имеет ни одного общего элемента
объема с понятием А «депутат» и одновременно они подчиняются
понятию В «человек».
Проверяем образовавшиеся отношения между понятиями А и В3 по
следующей схеме: «Ни один элемент объема А не является
элементом объема В3, и наоборот, а вместе они не исчерпывают
объем родового понятия В».
«Ни один «министр» не является «депутатом», и наоборот, а вместе
они не исчерпывают объем родового понятия В «человек».
Полученное высказывание является истинным, следовательно,
понятия подобраны правильно.

24.

А
В4
Отношение противоречия
Чтобы правильно подобрать противоречащее понятие В4,
необходимо работать в объеме родового понятия В «человек»,
прибавляя к его содержанию признак, которого нет у понятия А и
при этом объем понятия А и В4 должны исчерпывать обьем
понятия В
Понятие В4 «не-депутат» не имеет ни одного общего элемента
объема с понятием А «депутат» и одновременно они подчиняются
понятию В «человек».
Проверяем образовавшиеся отношения между понятиями А и В3 по
следующей схеме: «Ни один элемент объема А не является
элементом объема В3, и наоборот, а вместе они не исчерпывают
объем родового понятия В».
«Ни один «не-депутат» не является «депутатом», и наоборот, а
вместе они исчерпывают объем родового понятия В «человек».
Полученное высказывание является истинным, следовательно,
понятия подобраны правильно.

25.

Лекция 2. Понятие: виды и логические операции с ним
Вопрос 4.
Логические операции с понятиями

26.

4. Логические операции с понятиями
ЛОГИЧЕСКИЕ ОПЕРАЦИИ С ПОНЯТИЯМИ
ОГРАНИЧЕНИЕ ПОНЯТИЯ
ОБОБЩЕНИЕ ПОНЯТИЯ
ДЕЛЕНИЕ ПОНЯТИЯ
ОПРЕДЕЛЕНИЕ ПОНЯТИЯ
1. структурные
элементы
операции
2. виды операции
3. правила операции

27.

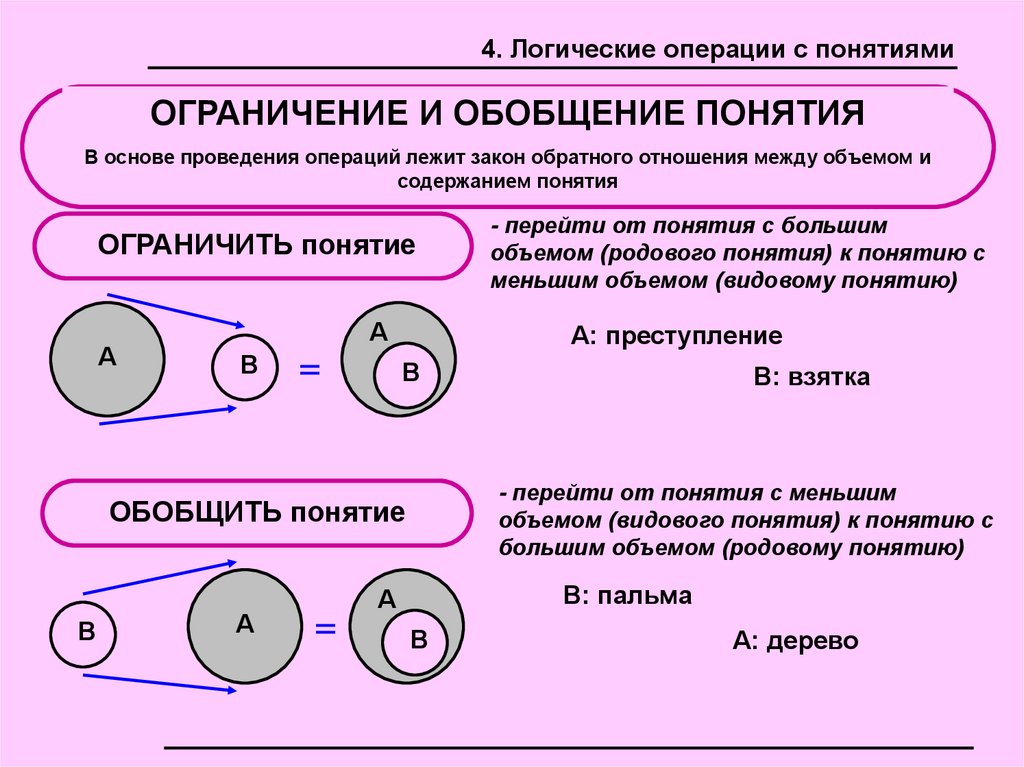
4. Логические операции с понятиями
ОГРАНИЧЕНИЕ И ОБОБЩЕНИЕ ПОНЯТИЯ
В основе проведения операций лежит закон обратного отношения между объемом и
содержанием понятия
ОГРАНИЧИТЬ понятие
А
А
В
=
А: преступление
В
А
=
В: взятка
- перейти от понятия с меньшим
объемом (видового понятия) к понятию с
большим объемом (родовому понятию)
ОБОБЩИТЬ понятие
В
- перейти от понятия с большим
объемом (родового понятия) к понятию с
меньшим объемом (видовому понятию)
В: пальма
А
В
А: дерево

28.

4. Логические операции с понятиями
ПРАВИЛА
ОГРАНИЧЕНИЯ И ОБОБЩЕНИЯ ПОНЯТИЯ
1. При обобщении или ограничении необходимо переходить только к
ближайшему родовому или видовому понятия.
Ошибка – скачок в ограничении, поспешное обобщение
2. Обобщать и ограничивать до бесконечности нельзя. Предел
обобщения – категории науки (у них нет родовых понятий). Предел
ограничения – единичные понятия - их объем невозможно уменьшить
3. Нельзя подменять логические операции обобщения и ограничения
операциями деления целого на части.

29.

Лекция 2. Понятие: виды и логические операции с ним
Практикум
Работа 1. Задание 2.

30.

Задание 2. Проведите последовательную многоступенчатую операцию
обобщения и ограничения понятия.
С
В
А
Дано понятие «отличник». Обозначим его А
Произведем логическую операцию обобщения, постепенно
подбирая родовые понятия и выполняя при этом правила
обобщения.
Понятие А: «отличник»
Понятие В: «успевающий учащийся»
Понятие С: «учащийся»
Проверяем образовавшиеся отношения между понятиями А и В:
«Всякий «отличник» является «успевающим учащимся», но не
наоборот. Полученное высказывание является истинным,
следовательно, понятия подобраны правильно.
Проверяем образовавшиеся отношения между понятиями В и С:
«Всякий «успевающий учащийся» является «учащимся», но не
наоборот. Полученное высказывание является истинным,
следовательно, понятия подобраны правильно.
Данная операция обобщения проведена правильно, так как все
правила операции обращения выполнены.

31.

А
Е
D
Произведем логическую операцию ограничения, постепенно
подбирая видовые понятия и выполняя при этом правила
ограничения.
Понятие А: «отличник»
Понятие E: «отличник из 3 «Б» класса»
Понятие D: «отличник из 3 «Б» класса школы №1»
Проверяем образовавшиеся отношения между понятиями Д и Е:
«Всякий «отличник 3 «Б» класса школы №1» является «отличник
из 3 «Б» класса», но не наоборот. Полученное высказывание
является истинным, следовательно, понятия подобраны правильно.
Проверяем образовавшиеся отношения между понятиями В и С:
«Всякий «отличник из 3 «Б» класса» является «отличником», но не
наоборот. Полученное высказывание является истинным,
следовательно, понятия подобраны правильно.
Данная операция ограничения проведена правильно, так как все
правила операции ограничения выполнены.

32.

4. Логические операции с понятиями
Должен быть почитаем,
как бог, тот, кто может
определять и делить
Платон
Миниатюра из рукописи XIII века
31

33.

4. Логические операции с понятиями
Точное логическое
определение понятий условие истинного знания
Сократ
40

34.

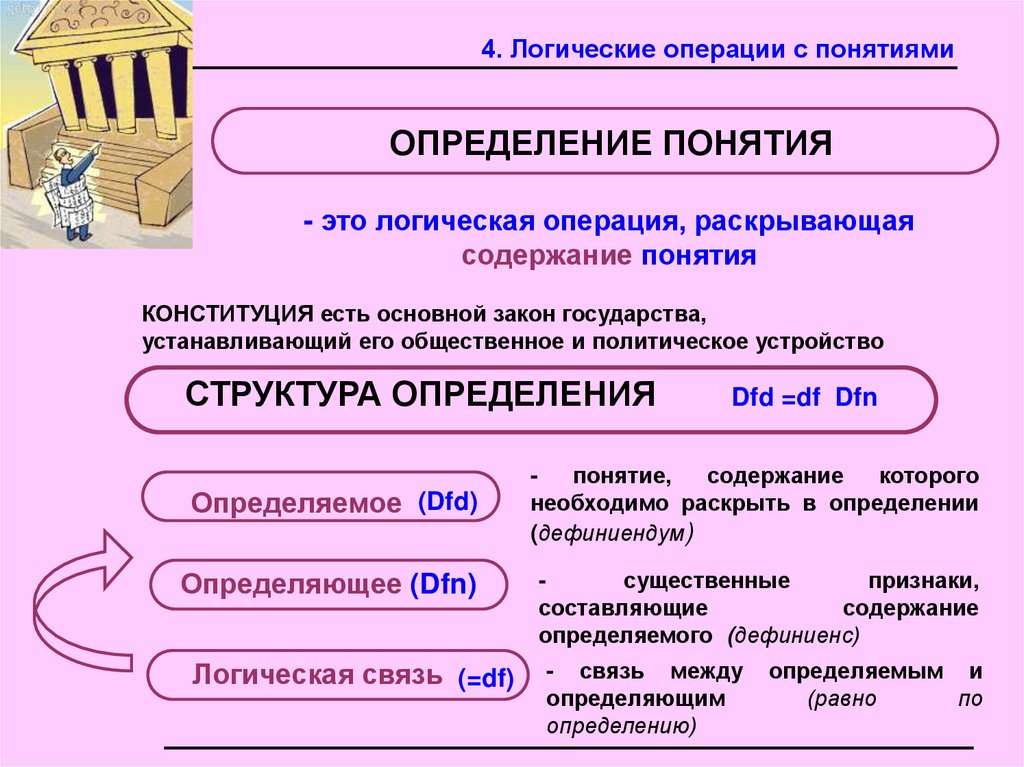
4. Логические операции с понятиями
ОПРЕДЕЛЕНИЕ ПОНЯТИЯ
- это логическая операция, раскрывающая
содержание понятия
КОНСТИТУЦИЯ есть основной закон государства,
устанавливающий его общественное и политическое устройство
СТРУКТУРА ОПРЕДЕЛЕНИЯ
Определяемое (Dfd)
Dfd =df Dfn
понятие,
содержание
которого
необходимо раскрыть в определении
(дефиниендум)
Определяющее (Dfn)
существенные
признаки,
составляющие
содержание
определяемого (дефиниенс)
Логическая связь (=df)
- связь между
определяющим
определению)
определяемым и
(равно
по

35.

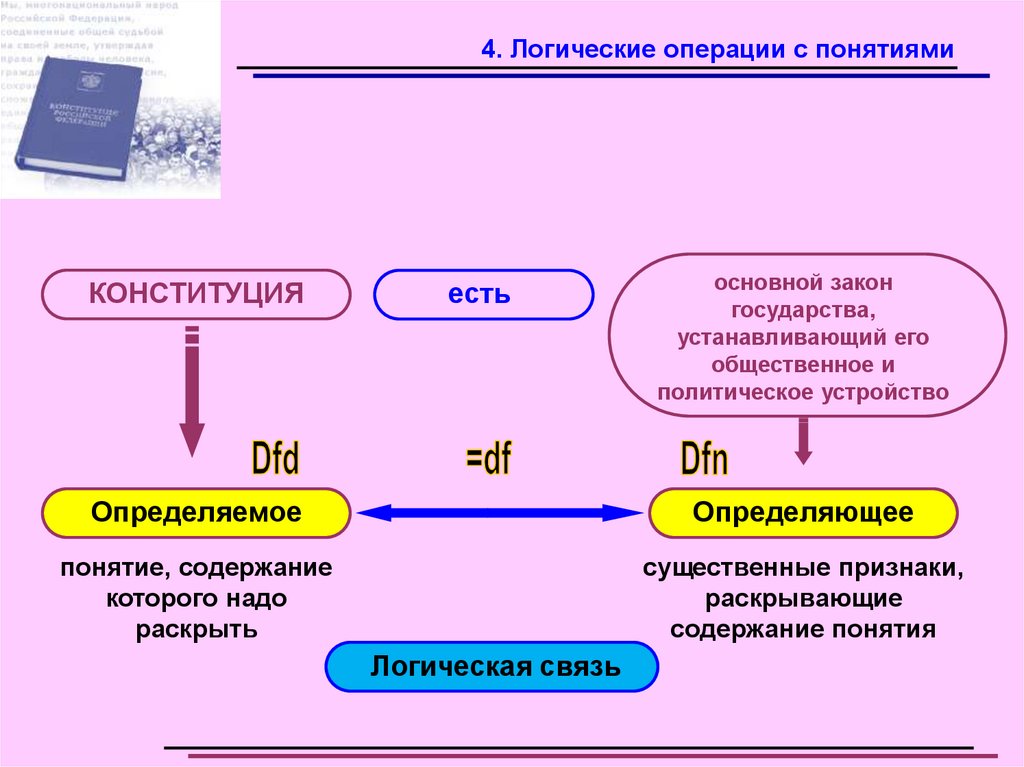
4. Логические операции с понятиями
КОНСТИТУЦИЯ
есть
основной закон
государства,
устанавливающий его
общественное и
политическое устройство
Определяемое
Определяющее
понятие, содержание
которого надо
раскрыть
существенные признаки,
раскрывающие
содержание понятия
Логическая связь

36.

4. Логические операции с понятиями
ВИДЫ ОПРЕДЕЛЕНИЙ
Родовидовые определения
Определяющая часть определения содержит родовое понятие и видовые
признаки
Пример: Великодушие - это качество человека, который не думает о собственной
выгоде, а в первую очередь беспокоится о других.
Определение через перечисление
Определяющая часть определения содержит перечисление предметов,
подпадающих под определяемое понятие
Пример: Беспощадность - это безжалостность, жестокосердие.
Определение через абстракцию
Определяющая часть определения содержит указание на отношение
равенства к чему-либо.
Пример: «Возраст (человека) — это общее, что присуще всем людям,
которые родились одновременно»

37.

4. Логические операции с понятиями
ВИДЫ РОДОВИДОВЫХ ОПРЕДЕЛЕНИЙ
Атрибутивно-реляционные
Видовое отличие – качества или свойства предметов, а также отношения
между ними.
Квадрат – это ромб с прямыми углами
Генетические
Видовое отличие – способ происхождения, образования предмета
Квадрат – это ромб, получаемый взаимно перпендикулярной установкой его
смежных сторон
Операциональные
Видовое отличие указывает на действие, позволяющее распознать
предмет
Квадрат – это такой ромб, что если к любой из ее сторон приложить основание
транспортира, совместив точку «0» с вершиной, то примыкающая к ней сторона
соединит точку «0» и отметку на шкале «90»

38.

4. Логические операции с понятиями
ПРАВИЛА ОПРЕДЕЛЕНИЯ
1. Определение должно быть соразмерным
Объём определяемого понятия должен быть равен объёму определяющего, то
есть они должны быть равнообъёмными
2. Определение не должно быть отрицательным
Отрицательное определение указывает на признаки, которые не принадлежат
предмету, но не указывает на признаки, принадлежащие предмету
3. Определение не должно содержать в себе круга
Если при определении понятия прибегают к другому понятию, которое, в
свою очередь, определяется при помощи первого, то такое определение
содержит в себе круг.
4. Определение должно быть четким, ясным
Оно должно указывать на известные признаки, не нуждающиеся в
определении и не содержащие двусмысленности.

39.

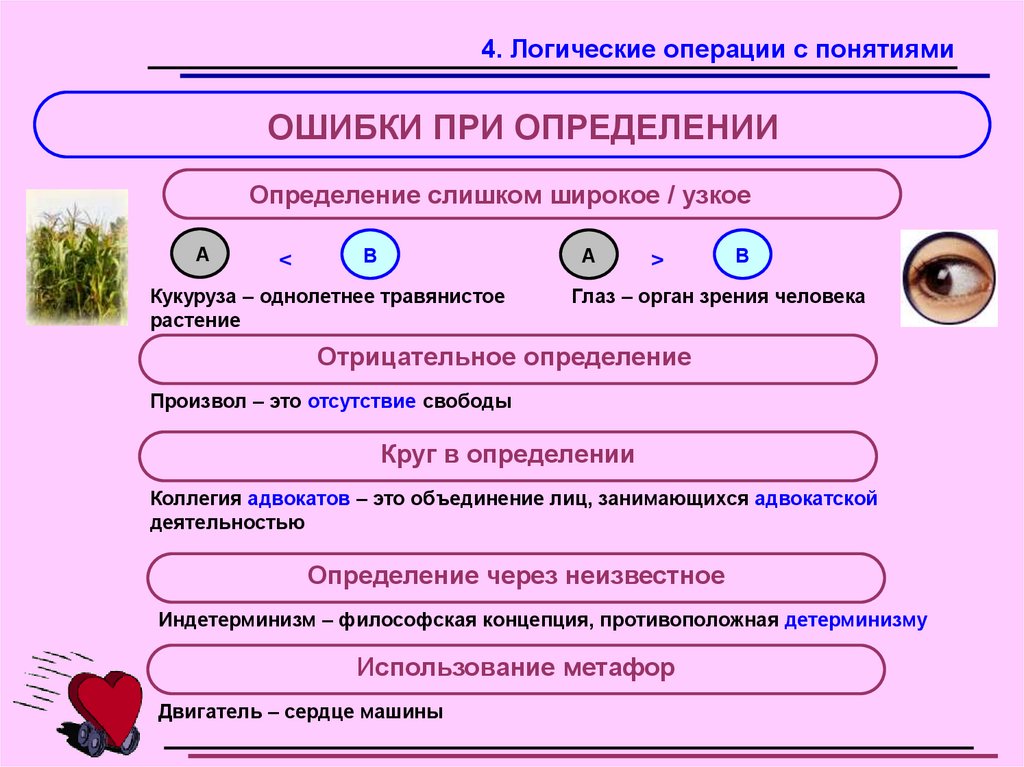
4. Логические операции с понятиями
ОШИБКИ ПРИ ОПРЕДЕЛЕНИИ
Определение слишком широкое / узкое
А
<
В
А
Кукуруза – однолетнее травянистое
растение
>
В
Глаз – орган зрения человека
Отрицательное определение
Произвол – это отсутствие свободы
Круг в определении
Коллегия адвокатов – это объединение лиц, занимающихся адвокатской
деятельностью
Определение через неизвестное
Индетерминизм – философская концепция, противоположная детерминизму
Использование метафор
Двигатель – сердце машины

40.

4. Логические операции с понятиями
ПРИЕМЫ, СХОДНЫЕ С ЯВНЫМ ОПРЕДЕЛЕНИЕМ
Указание
Разъяснение путем непосредственного указывания на предметы
Описание
Перечисление некоторых внешних признаков предмета
Характеристика
Указание признаков, отличительных в каком-либо отношении
Сравнение
Указание на некоторые общие черты предметов класса

41.

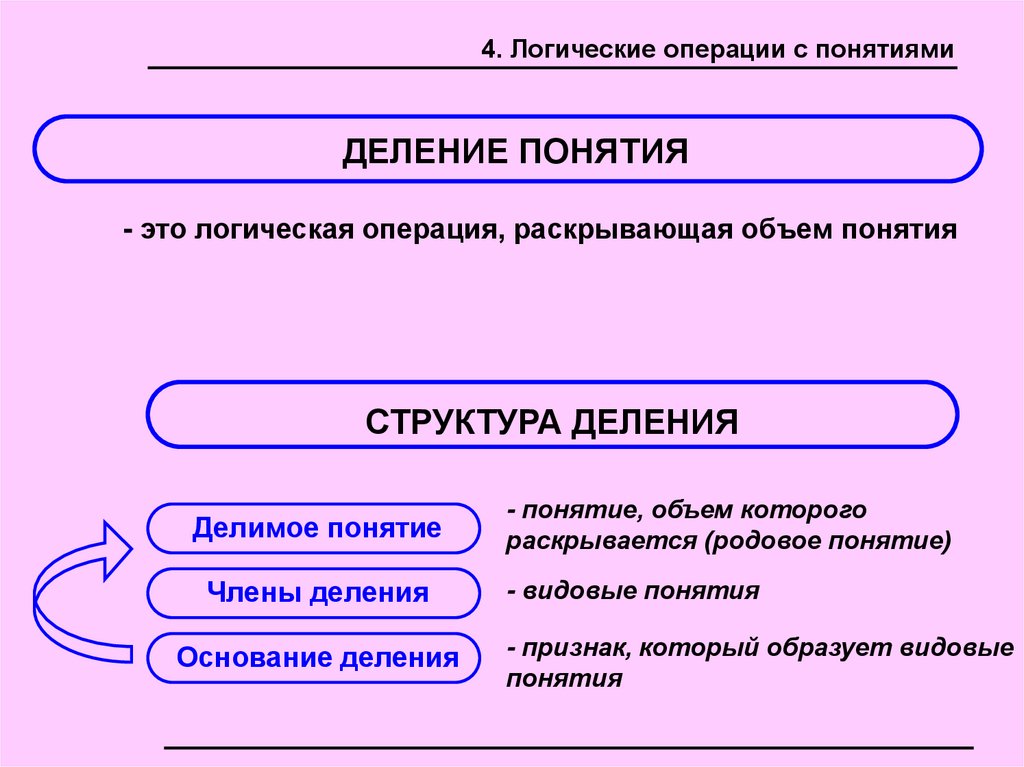
4. Логические операции с понятиями
ДЕЛЕНИЕ ПОНЯТИЯ
- это логическая операция, раскрывающая объем понятия
СТРУКТУРА ДЕЛЕНИЯ
Делимое понятие
- понятие, объем которого
раскрывается (родовое понятие)
Члены деления
- видовые понятия
Основание деления
- признак, который образует видовые
понятия

42.

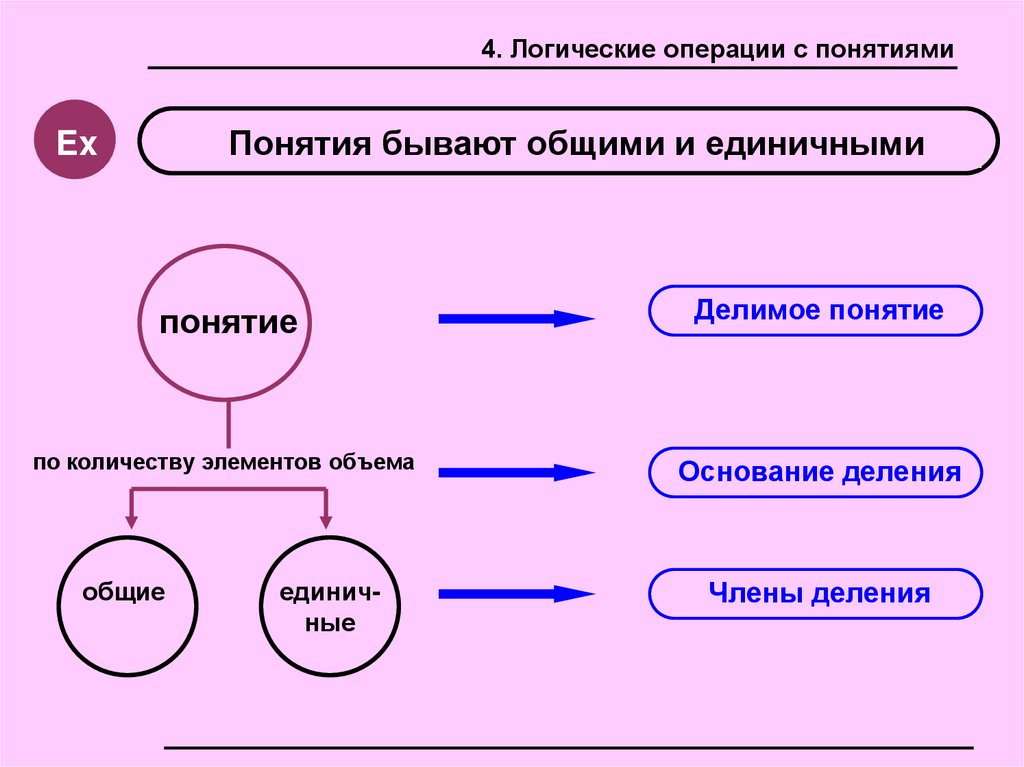
4. Логические операции с понятиями
Понятия бывают общими и единичными
Ex
понятие
Делимое понятие
по количеству элементов объема
Основание деления
общие
единичные
Члены деления

43.

4. Логические операции с понятиями
ВИДЫ ДЕЛЕНИЯ
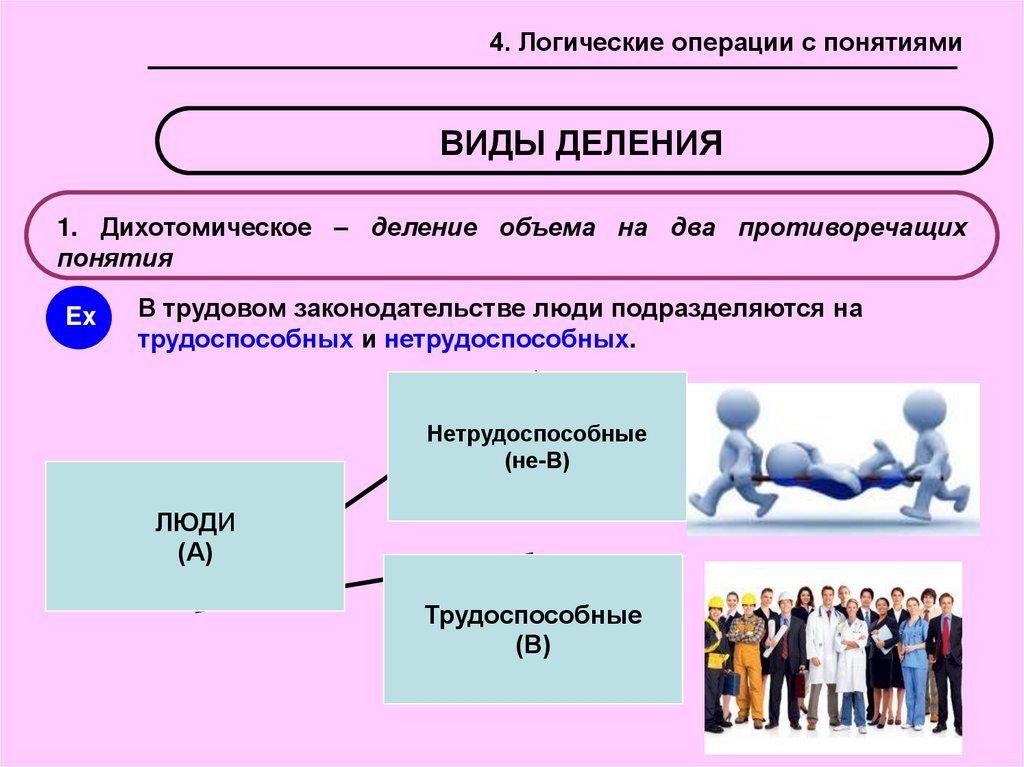
1. Дихотомическое – деление объема на два противоречащих
понятия
Ex
В трудовом законодательстве люди подразделяются на
трудоспособных и нетрудоспособных.
Нетрудоспособные
(не-В)
ЛЮДИ
(А)
Трудоспособные
(В)

44.

4. Логические операции с понятиями
ВИДЫ ДЕЛЕНИЯ
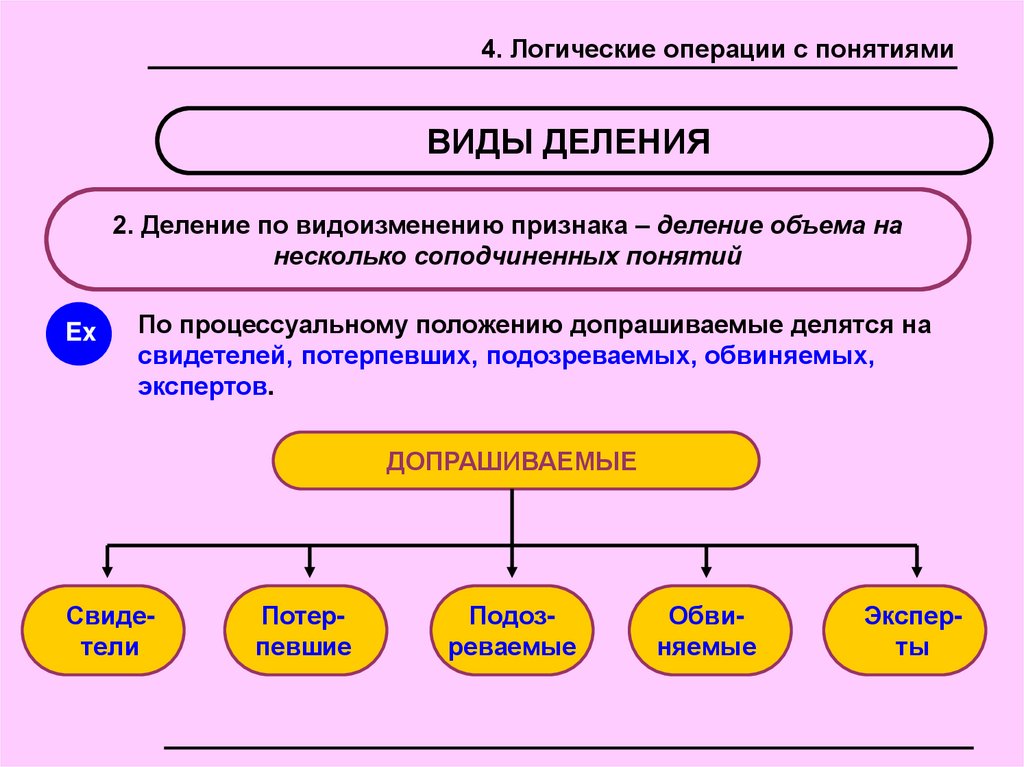
2. Деление по видоизменению признака – деление объема на
несколько соподчиненных понятий
Ex
По процессуальному положению допрашиваемые делятся на
свидетелей, потерпевших, подозреваемых, обвиняемых,
экспертов.
ДОПРАШИВАЕМЫЕ
Свидетели
Потерпевшие
Подозреваемые
Обвиняемые
Эксперты

45.

4. Логические операции с понятиями
ПРАВИЛА ДЕЛЕНИЯ
1. Соразмерность
Сумма объёмов членов деления должна совпадать с объёмом делимого
понятия.
2. Единство основания
Деление должно быть выполнено по одному основанию
3. Несовместимость
Члены деления должны быть несовместимыми понятиями, то есть
исключать друг друга.
4. Непрерывность
При делении нельзя сразу переходить к подвиду от рода, минуя вид. Нельзя
допускать «скачки»: деление нужно выполнять последовательно.

46.

4. Логические операции с понятиями
ОШИБКИ ПРИ ДЕЛЕНИИ
Неполнота деления / излишество в делении
Смешение оснований деления
Пересечение объемов членов деления
Скачок в делении

47.

4. Логические операции с понятиями
ОШИБКИ ПРИ ДЕЛЕНИИ
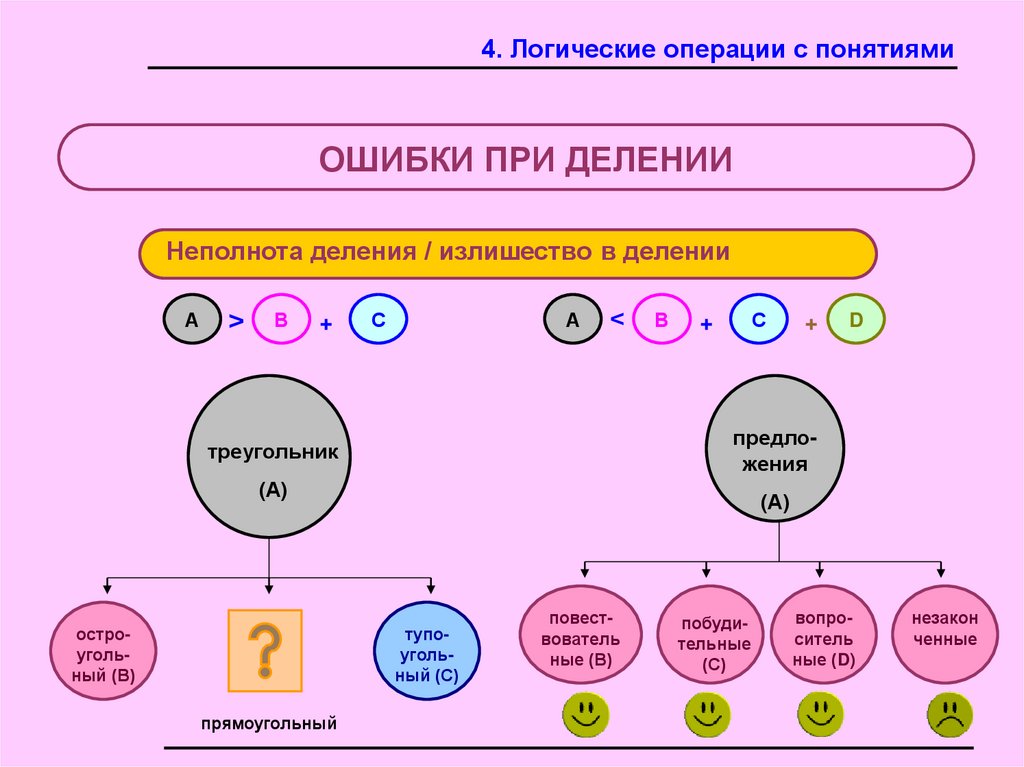
Неполнота деления / излишество в делении
А
>
В
+
С
А
<
В
С
+
(А)
(А)
тупоугольный (С)
прямоугольный
D
предложения
треугольник
остроугольный (В)
+
повествователь
ные (В)
побудительные
(С)
вопроситель
ные (D)
незакон
ченные

48.

4. Логические операции с понятиями
ОШИБКИ ПРИ ДЕЛЕНИИ
Смешение оснований деления
Ex
Население делится на мужчин и женщин, стариков и детей

49.

4. Логические операции с понятиями
ОШИБКИ ПРИ ДЕЛЕНИИ
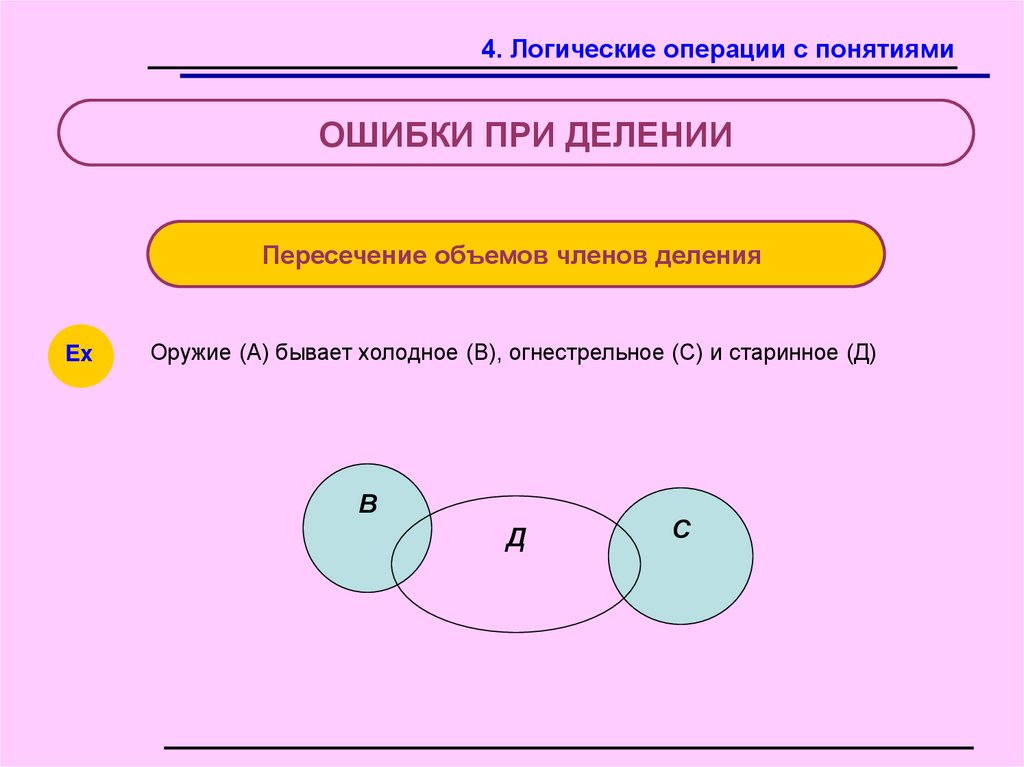
Пересечение объемов членов деления
Ex
Оружие (А) бывает холодное (В), огнестрельное (С) и старинное (Д)
В
Д
С

50.

4. Логические операции с понятиями
ОШИБКИ ПРИ ДЕЛЕНИИ
Скачок в делении
Ex
Геометрические фигуры (родовое понятие) делятся на плоские,
объемные (видовые понятие), треугольники и квадраты (подвидовые
понятия).

51.

Лекция 2. Понятие: виды и логические операции с ним
Практикум
Работа 1. Задание 3.
Задание 3. Для понятия проведите операцию определения и деления. Проведите
анализ произведенных операций (структура, вид). Проверьте правильность
операции.

52.

Выпишите понятие, соответствующее вашему варианту для задания 3 из Приложения
«латентная преступность»
С помощью необходимой справочной литературы сформулируйте определение данного
понятия «Латентная преступность – преступность, не получившая по тем или
иным причинам отражения в официальной уголовной статистике».
Структура определения:
Определяемое понятие: латентная преступность
Определяющее понятие: преступность, не получившая по тем или иным причинам
отражения в официальной уголовной статистике
Вид определения: явное, родовидовое, атрибутивное
Если это родовидовое определение, то в определяющем понятии выделите
- родовое понятие: преступность
- видовое отличие: не получение по тем или иным причинам отражения в
официальной уголовной статистике
Операция определения является правильной / неправильной (нужное подчеркнуть),
так нарушено правило неотрицательности.

53.

Для того, чтобы правильно начать производить операцию деления понятия
«латентная преступность» сначала задайте основание для деления
«обстоятельств, которые привели к тому, что преступление осталось
скрытым»
С помощью необходимой справочной литературы произведите операцию деления понятия
«В зависимости от обстоятельств, которые привели к тому, что
преступление осталось скрытым, выделяют естественную, искусственную и
пограничную латентность»
Структура деления:
Делимое понятие: латентная преступность
Члены деления:
1-й член деления: естественная латентность
2-й член деления: искусственная латентность
3-й член деления: пограничная латентность
Вид деления: деление по видоизменению основания
Операция деления является правильной / неправильной (нужное подчеркнуть),
так как все правила деления выполнены

54.

4. Логические операции с понятиями
КЛАССИФИКАЦИЯ
- это логическая операция, состоящая в систематическом
распределении элементов объёма понятия по классам,
представляющая собой вид последовательного деления
КЛАССИФИКАЦИЯ РЕШАЕТ ТРОЙСТВЕННУЮ ЗАДАЧУ
Упорядочивает множество исследуемых объектов
Делает множество хорошо обозримым
Облегчает доступ в памяти к любому виду объектов
данного множества
27

55.

4. Логические операции с понятиями
КЛАССИФИКАЦИЯ И ЕЕ ВИДЫ
Естественная
Искусственная
в ее основании лежат существенные
для выделяемых классов признаки, из
которых вытекают производные
свойства упорядочиваемых объектов
в ее основании лежат несущественные
для выделяемых классов признаки
Ex
Тематический каталог книг в библиотеке
Ex
Алфавитный каталог книг в библиотеке
В XVIII-XIX вв. всеобщую известность получила классификация живых
существ К. Линнея, шведского натуралиста.
Его классификация объектов – элементов живой и неживой природы –
должна была бы выявить основные принципы, определяющие строение
мира, и дать полное и глубокое объяснение природы.
Ведущей идеей Линнея было противопоставление естественной и
искусственной классификаций. По мысли Линнея и его последователей,
всеобъемлющие естественные классификации являются высшей
целью изучения природы и венцом научного её познания.

56.

Логические операции с понятиями
Научная классификация
систематизирует результаты
предшествующего развития отрасли
знания и намечает перспективу
дальнейших исследований
ПЕРИОДИЧЕСКАЯ СИСТЕМА ЭЛЕМЕНТОВ
Д.И.МЕНДЕЛЕЕВА
фиксирует закономерные связи между химическими
элементами
определяет место каждого из них в единой
таблице
Эта таблица позволила сделать подтвердившиеся
прогнозы относительно неизвестных ещё элементов.
Исследование сложных и динамичных социальных объектов и явлений
выявило относительность и приблизительность каждой классификации.
Было открыто существование переходных форм, которые трудно
однозначно отнести к той или иной определённой группе. Иногда эта
переходная группа составляет самостоятельную группу (вид).
При классификации наук возникают такие переходные формы, как
биохимия, геохимия, космическая медицина, астрофизика и др.

57.

4. Логические операции с понятиями
Классификация в гуманитарных науках
Во второй половине XX века общепризнанной считалась классификация терроризма,
созданная директором Французского института криминологии Ксавье Роффером. Он
выделял терроризм
идеологический,
националистический,
этнический,
патологический и
государственный.
После «холодной войны» ультраправые и ультралевые «идеологи», постоянно
провоцировавшие друг друга бомбами, стали реже напоминать о себе. Все меньше
этнических меньшинств пробуют силой доказать свой «суверенитет».
Зато доктору Рофферу пришлось внести в свою схему «религиозный
терроризм».
А. Сабов. Последний взгляд Бога// Российская газета, № 224, 12 октября 2004 г. С. 14.