ВЕКТОРЫ ОСНОВНАЯ

1. Векторы в пространстве

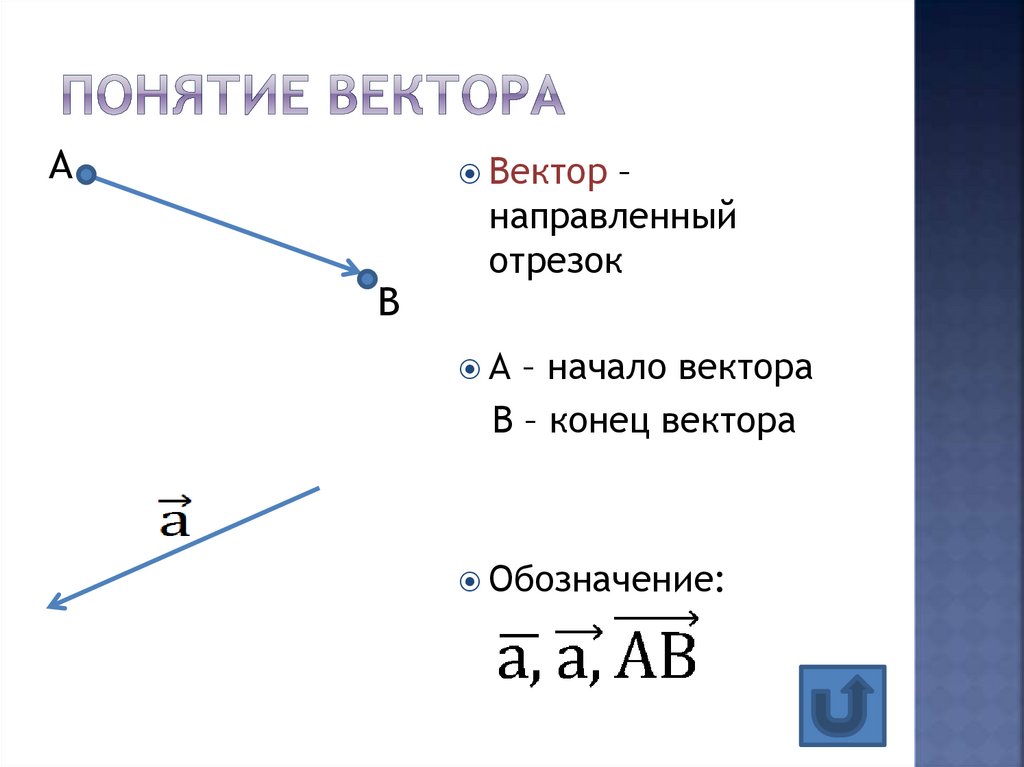
2. Понятие вектора

А
Вектор –
В
направленный
отрезок
А – начало вектора
В – конец вектора
Обозначение:

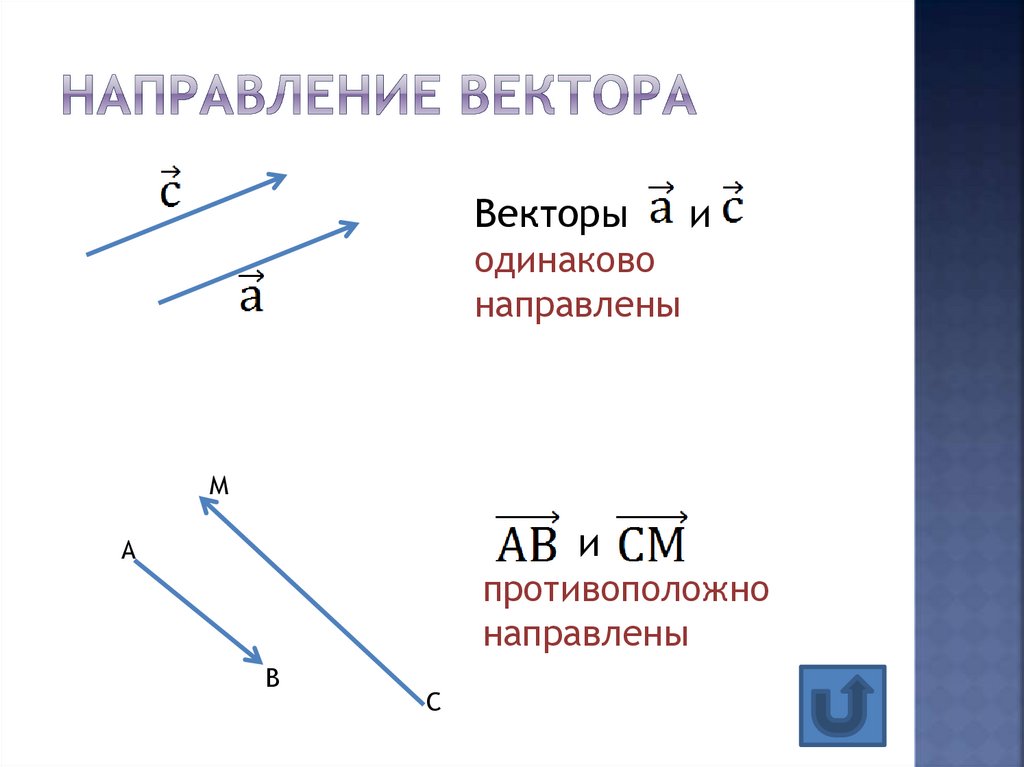
3. Направление вектора

Векторы
и
одинаково
направлены
М
и
А
противоположно
направлены
В
С

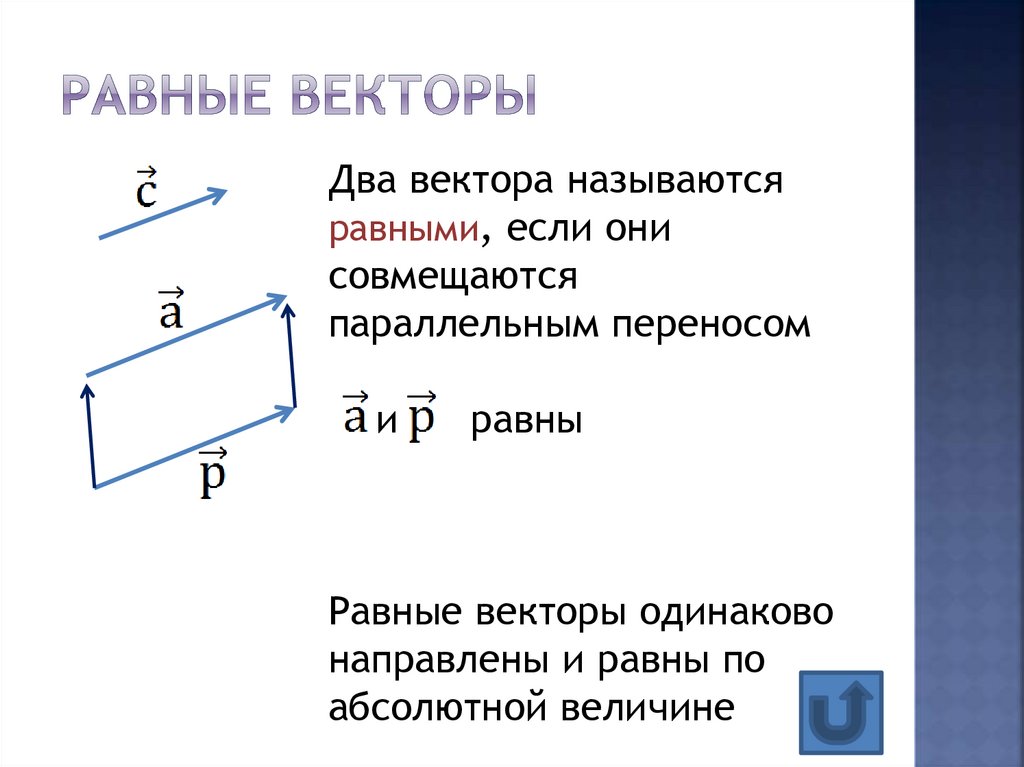
4. Равные векторы

Два вектора называются
равными, если они
совмещаются
параллельным переносом
и
равны
Равные векторы одинаково
направлены и равны по
абсолютной величине

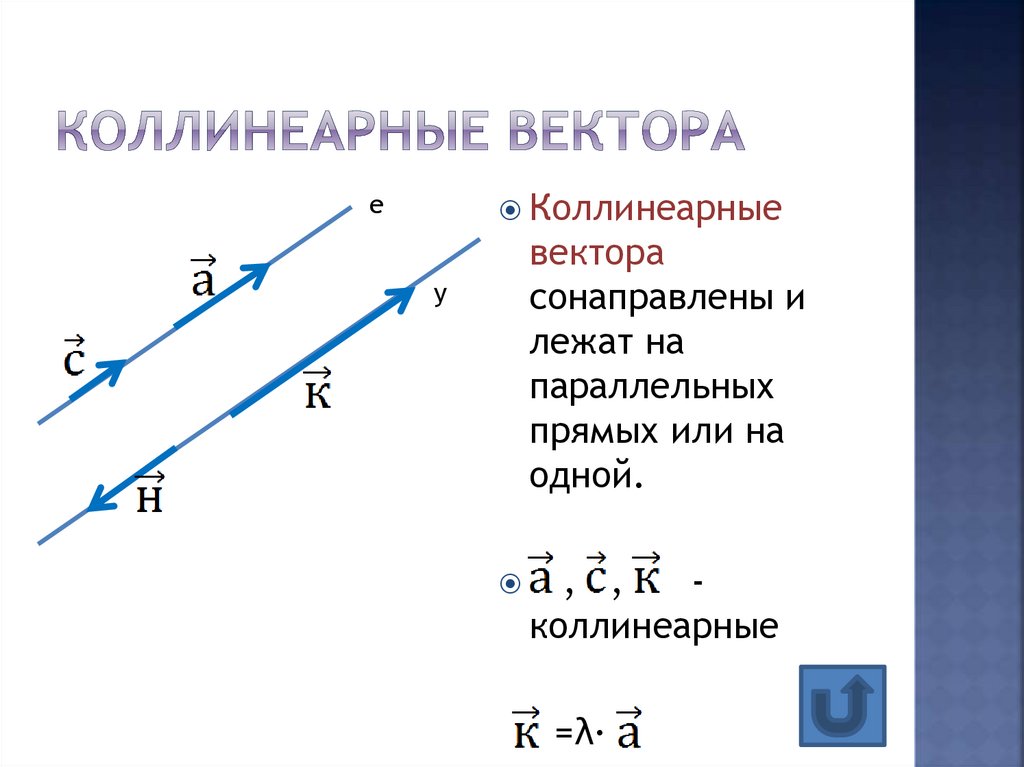
5. Коллинеарные вектора

Коллинеарные
е
вектора
сонаправлены и
лежат на
параллельных
прямых или на
одной.
у
, ,
коллинеарные
=λ∙

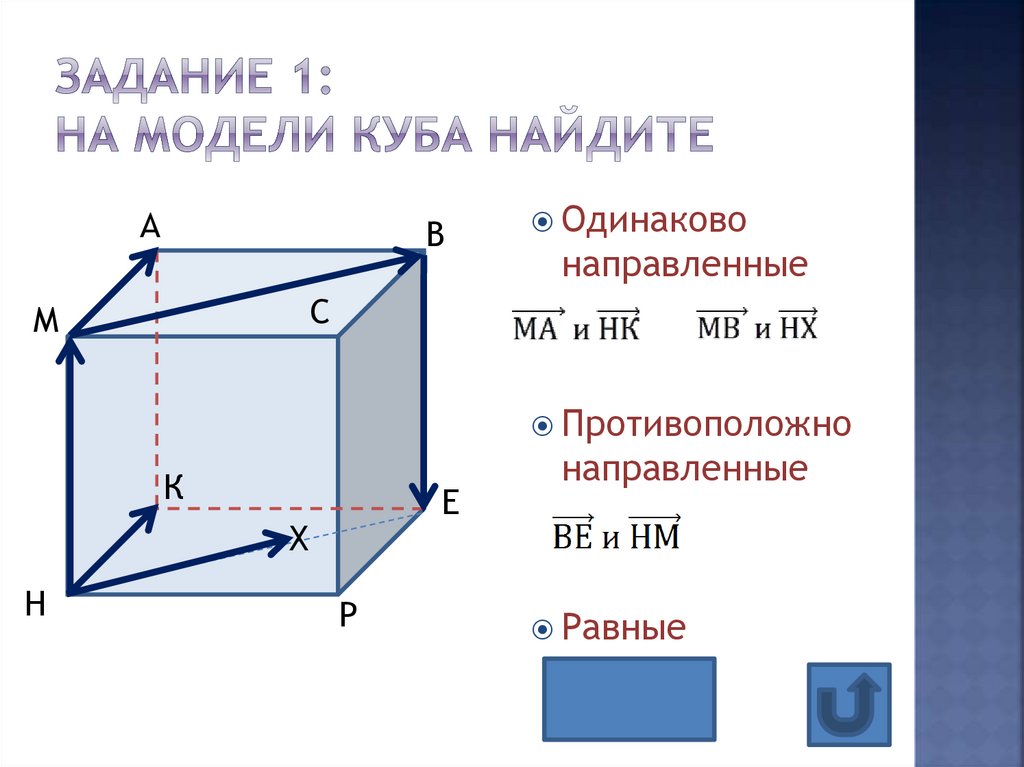
6. Задание 1: на модели куба найдите

А
В
Одинаково
направленные
С
М
Противоположно
К
Е
Х
Н
Р
направленные
Равные

7. Абсолютная величина вектора

Абсолютная величина
(или модуль) вектора
– длина отрезка,
изображающего
вектор
Обозначение:
Нулевой вектор – вектор, у
которого начало совпадает
с его концом

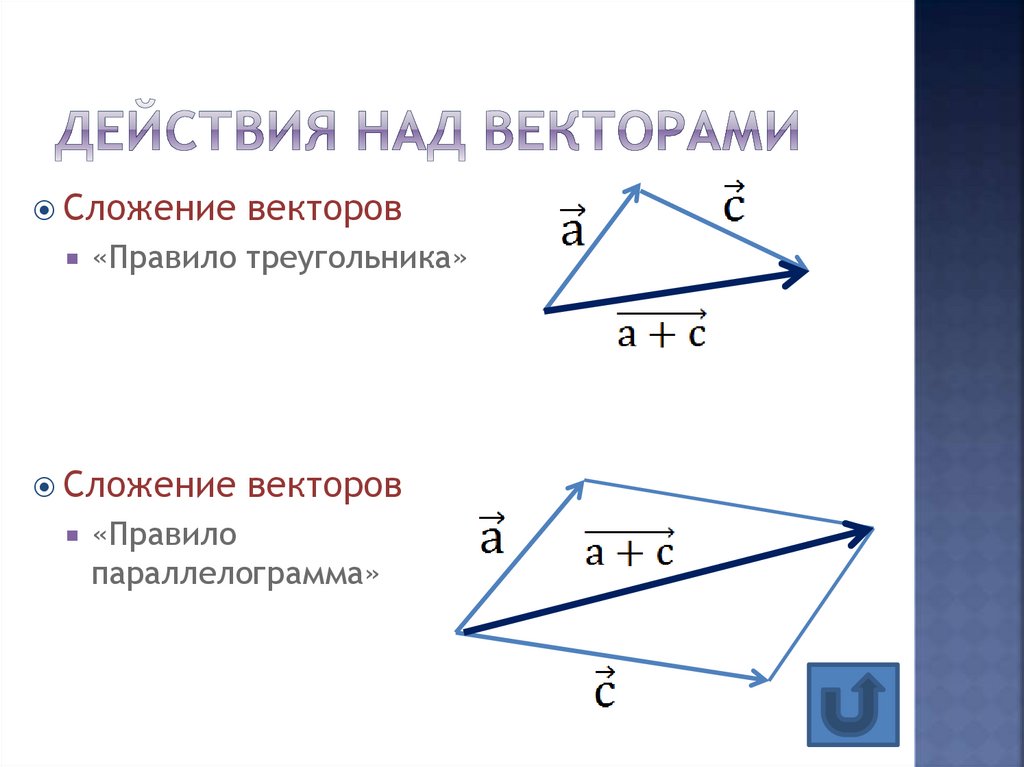
8. Действия над векторами

Сложение векторов
«Правило треугольника»
Сложение векторов
«Правило
параллелограмма»

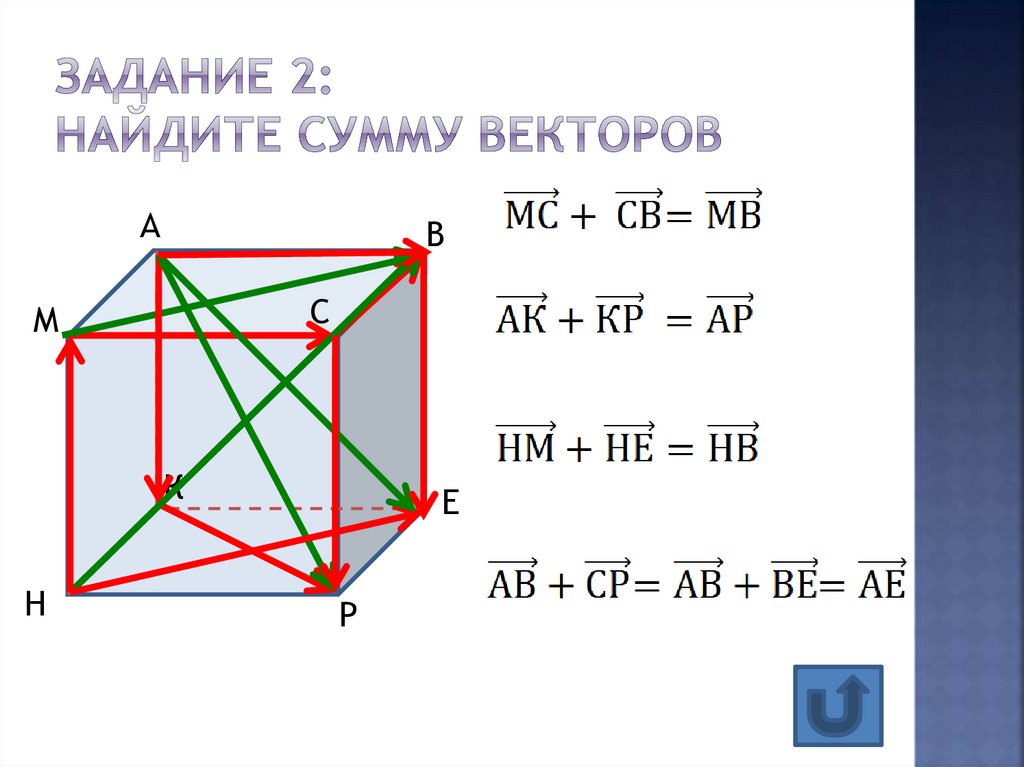
9. Задание 2: найдите сумму векторов

А
В
С
М
К
Н
Е
Р

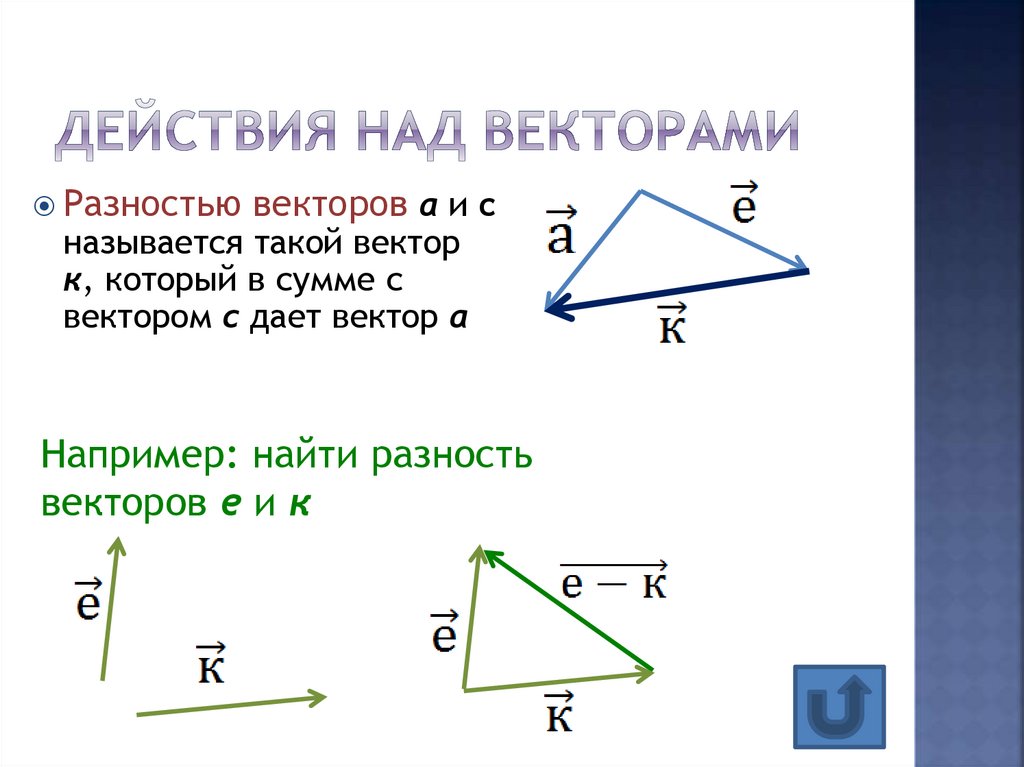
10. Действия над векторами

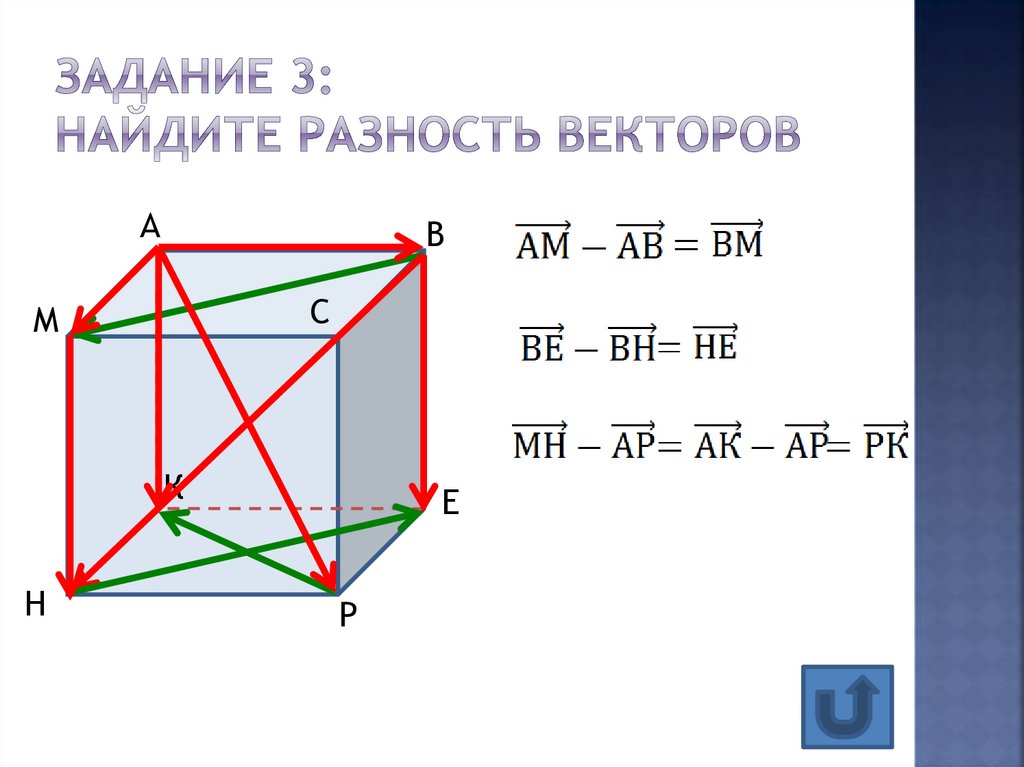
Разностью векторов а и с
называется такой вектор
к, который в сумме с
вектором с дает вектор а
Например: найти разность
векторов е и к

11. Задание 3: найдите разность векторов

А
В
С
М
К
Н
Е
Р

12. Тезаурус по теме «Векторы в пространстве»

Вектор, направление,
абсолютная величина
Координаты вектора в
Задание 4
пространстве
Равные вектора
Сложение векторов в
пространстве
Умножение вектора на
число
Скалярное произведение
Задание 5
векторов

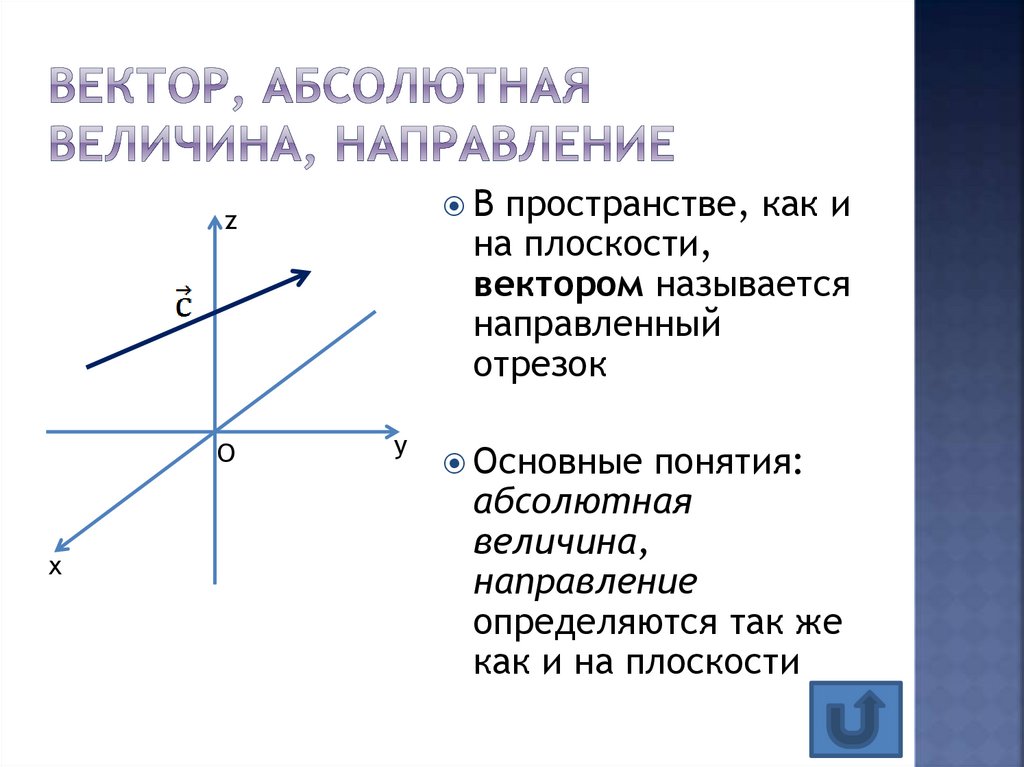
13. Вектор, абсолютная величина, направление

В пространстве, как и
z
O
x
на плоскости,
вектором называется
направленный
отрезок
y
Основные понятия:
абсолютная
величина,
направление
определяются так же
как и на плоскости

14. Координаты вектора в пространстве

Координаты вектора
А(х1;у1;z1)
z
B(x2;y2;z2)
В
(x2-х1;y2-у1;z2-z1)
Пример:
определить координаты
если М(9;3;-6) и С(-5; 4;-1)
(-5-9; 4-3; -1-(-6))
(-14;1;5)
А
O
,
x
y

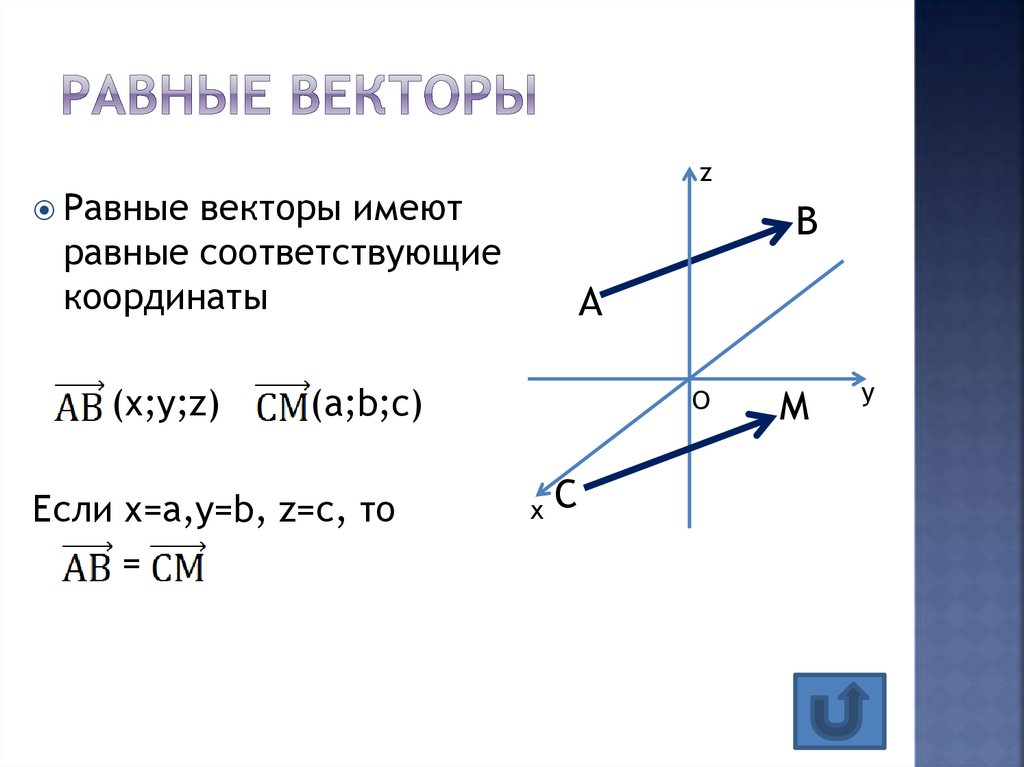
15. Равные векторы

z
Равные векторы имеют
В
равные соответствующие
координаты
(х;y;z)
А
(a;b;c)
Если х=а,у=b, z=с, то
=
O
x С
М
y

16. Задание 4: укажите пары равных векторов

Дано:
А(2;7;-3); В(1;0;3); С(-3;-4;5); М(-2;3;-1)
Определить: пары равных векторов