Логарифмические неравенства

1. Логарифмические неравенства

2.

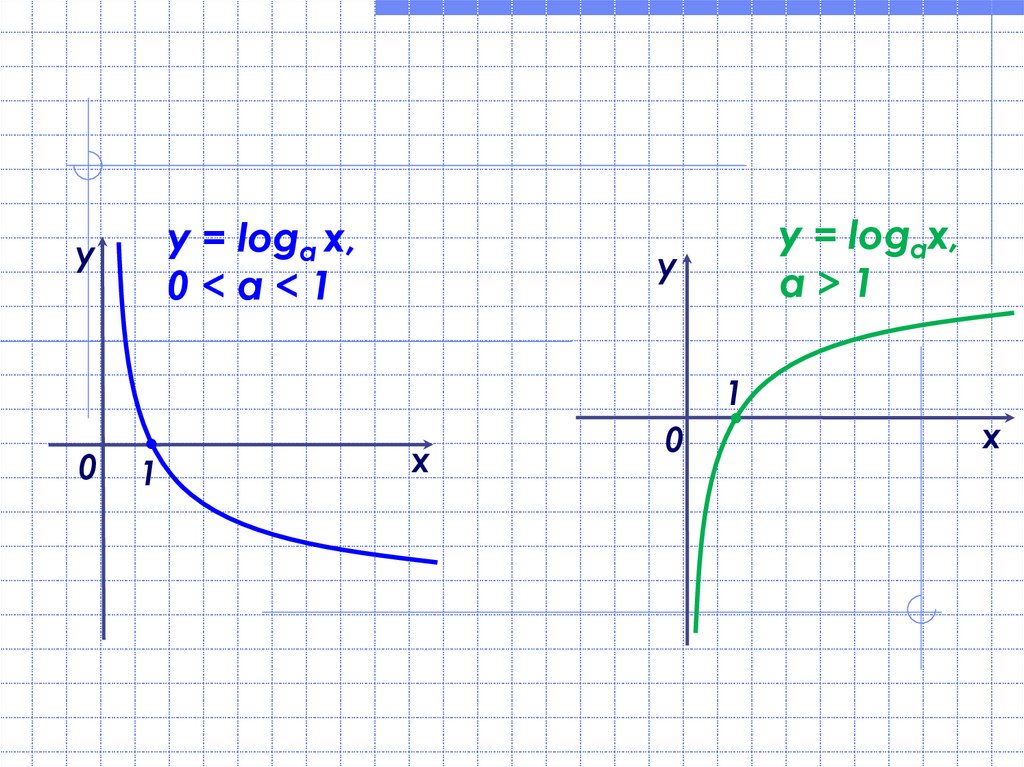
y = loga х,
0<а<1
у
y = logax,
а>1
у
1
х
1
х
0
0

3. Логарифмические неравенства

Неравенства вида loga f(x) > logа g(х), где а ≠ 1, a > 0
называют логарифмическими неравенствами
loga f(x) > logа g(х)
а>1
или
0<а<1

4. Решение неравенств

1. Решение логарифмических неравенств сводиться к
решению системы неравенств, содержащих область
определения функции и решение равносильного неравенства,
полученного из логарифмического неравенства, путем его
преобразований
по
известным
нам
свойствам
логарифмических функций.
2. Важным пунктом при решении логарифмического
неравенства является так же монотонность функции:
1. Если logax1<logax2 , при этом аa>1>1 (т.е функция ↑)
x1<x2 (знак остается прежним)
2. Если logax1<logax2 , при этом 0<a<1 (т.е функция ↓)
x1>x2 (знак меняется на противоположный)

5. Схема решения логарифмических неравенств

1. Найти ООФ
2. Решить логарифмическое неравенство, применяя :
- свойства логарифмов( сужать ООФ нельзя, т.е нельзя
логарифмировать );
- монотонность логарифмической функции( возрастание
и убывания функции).
3. Выбрать общее решение между ООФ и решением
неравенства (1 2)

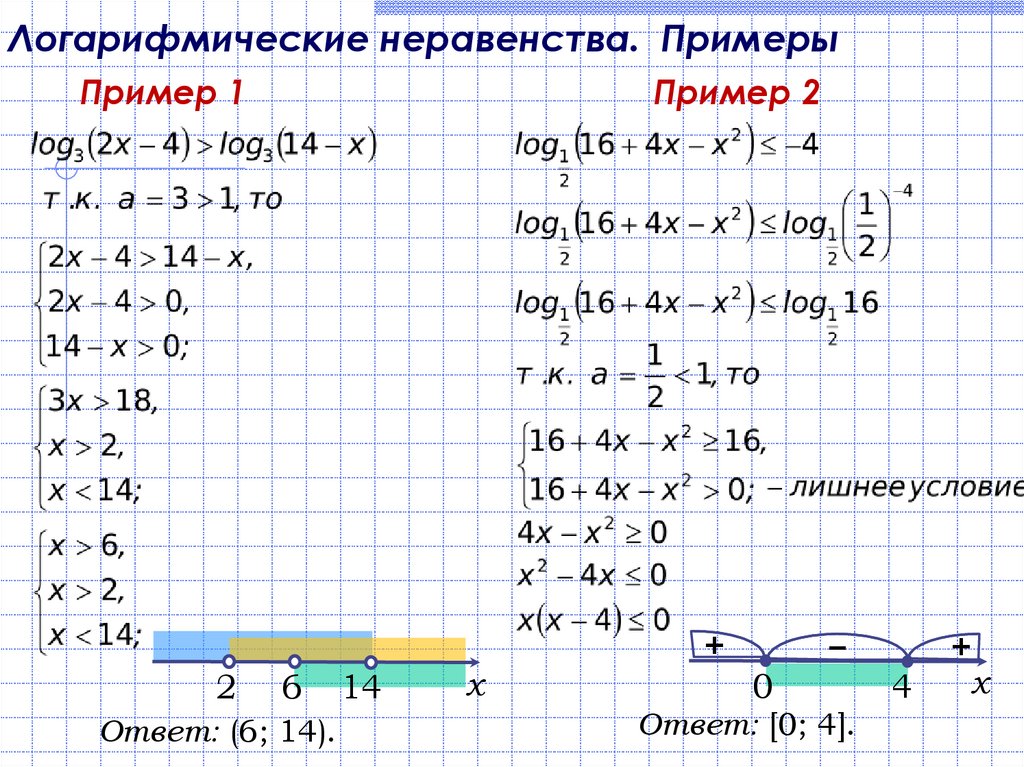
6. Логарифмические неравенства. Примеры

Пример 1
2
Пример 2
6
Ответ: (6; 14).
14
х
+
0
−
Ответ: [0; 4].
4
+
х

7.

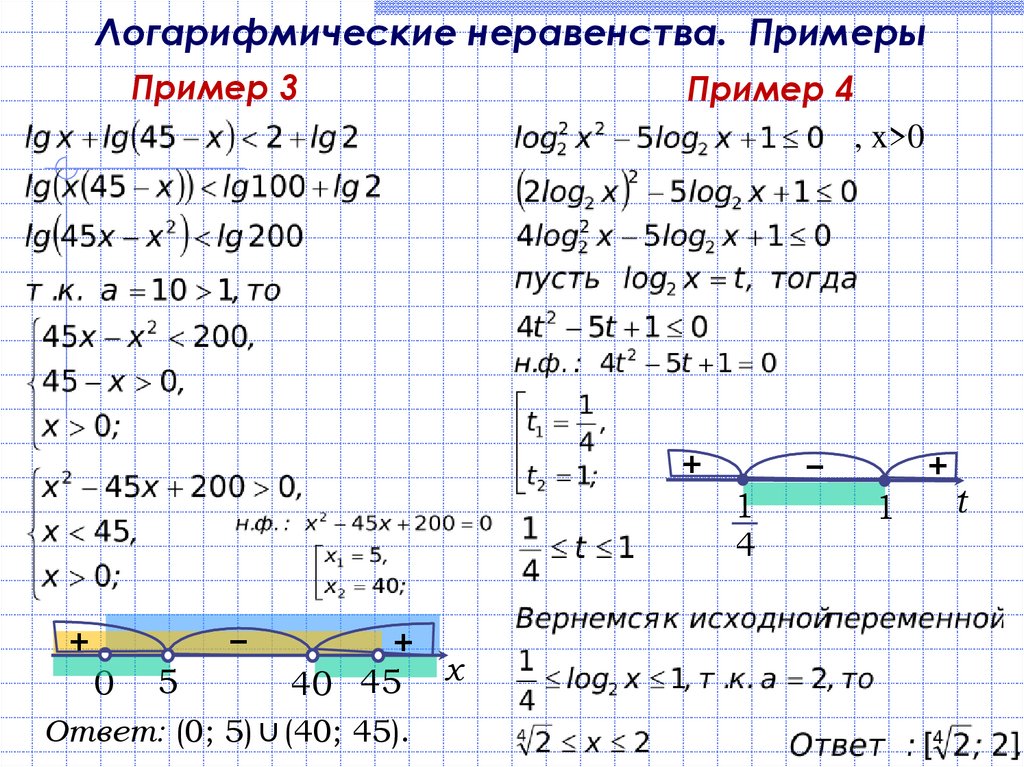
Логарифмические неравенства. Примеры
Пример 3
Пример 4
, x>0
+
1
4
+
0
5
−
+
40 45 х
Ответ: (0; 5) ∪ (40; 45).
−
+
1
t

8.

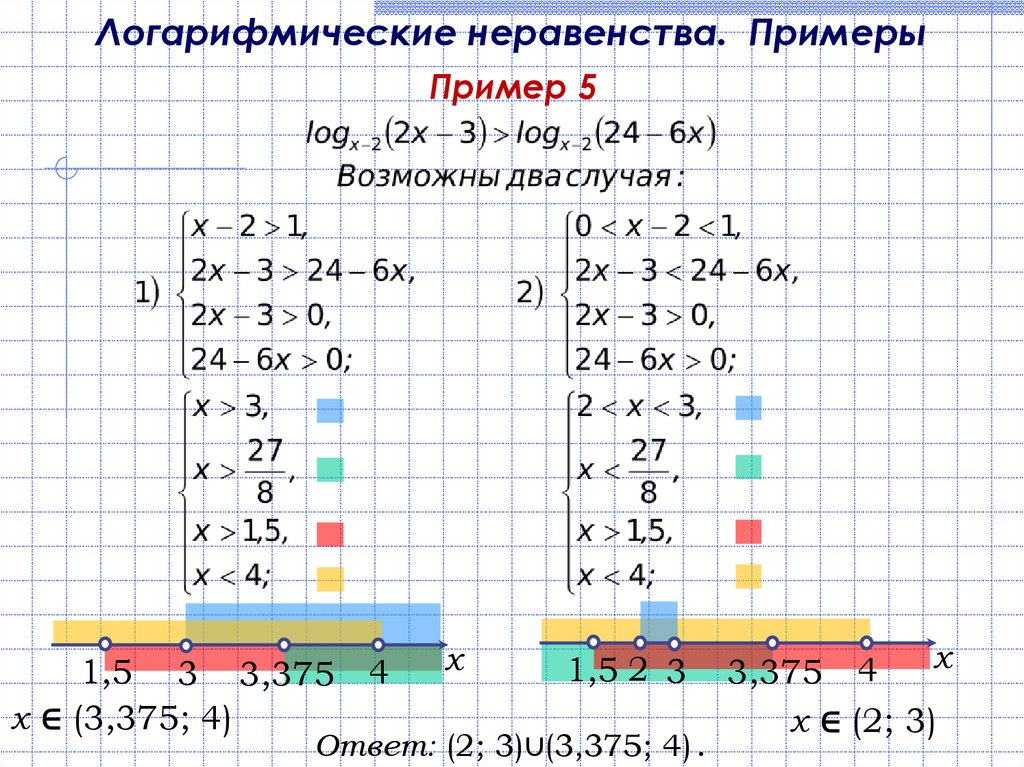
Логарифмические неравенства. Примеры
Пример 5
1,5 3 3,375 4
x ∈ (3,375; 4)
х
1,5 2 3
Ответ: (2; 3)∪(3,375; 4) .
х
3,375 4
x ∈ (2; 3)

9. Закрепление пройденного материала Самостоятельная работа

I вариант
1. log3(x+2)<3
2. log1/5(4-3x)≥-1
3. log0,3(2x+5)≥log0,3(x+1)
II вариант
1. log3(x+1)<-2
2. log1/2(3-5x)<-3
3. log3(5-4x)<log3(x-1)