Word-Problems

1. Word Problems

COIN PRIBLEMS
CONSECUTIVE INTEGER PROBLEMS
AGE PROBLEMS
PERCENT: INTEREST PROBLEMS
MIXTURE PROBLEMS
MOTION PROBLEMS
WORK PROBLEMS
DISCOUNT AND PROFIT PROBLEMS

2. A. Coin Problems

In solving coin problems, it is best to change the
value of all monies involved to cents before writing
an equation. Thus, the number of nickels must be
multiplied by 5 to give their value in cents; dimes
must be multiplied by 10; quarters by 25; halfdollars by 50; and dollars by 100.
Ex. Richard has $3.50 consisting of nickels and
dimes. If he has 5 more dimes than nickels, how
many dimes does he have?

3. B. Consecutive Integer Problems

Consecutive integers are one apart and can be
represented by x, x + 1, x + 2, etc. Consecutive even
or odd integers are two apart and can be represented
by x, x + 2, x + 4, etc.
Ex. Three consecutive odd integers have a sum of 33.
Find the average of these integers.

4. C. Age Problems

Problems of this type usually involve a comparison of
ages at the present time, several years from now, or
several years ago. A person’s age x years from now is
found by adding x to his present age. A person’s age x
years ago is found by subtracting x from his present
age.
Ex. Michelle was 12 years old y years ago. Represent
her age b years from now.

5. D. Interest Problems

The annual amount of interest paid on an investment
is formed by multiplying the amount of principal
invested by the rate (percent) of interest paid.
Ex. Mr. Strauss invests $4,000, part at 6% and part
at 7%. His income from these investments in one
year is $250. Find the amount invested at 7%.

6. D. Interest Problems

Interest can be computed in two basic ways.
With simple annual interest, the interest is
computed on the principal only and is equal to
If interest is compounded, then interest is
computed on the principal as well as on any interest
already earned.

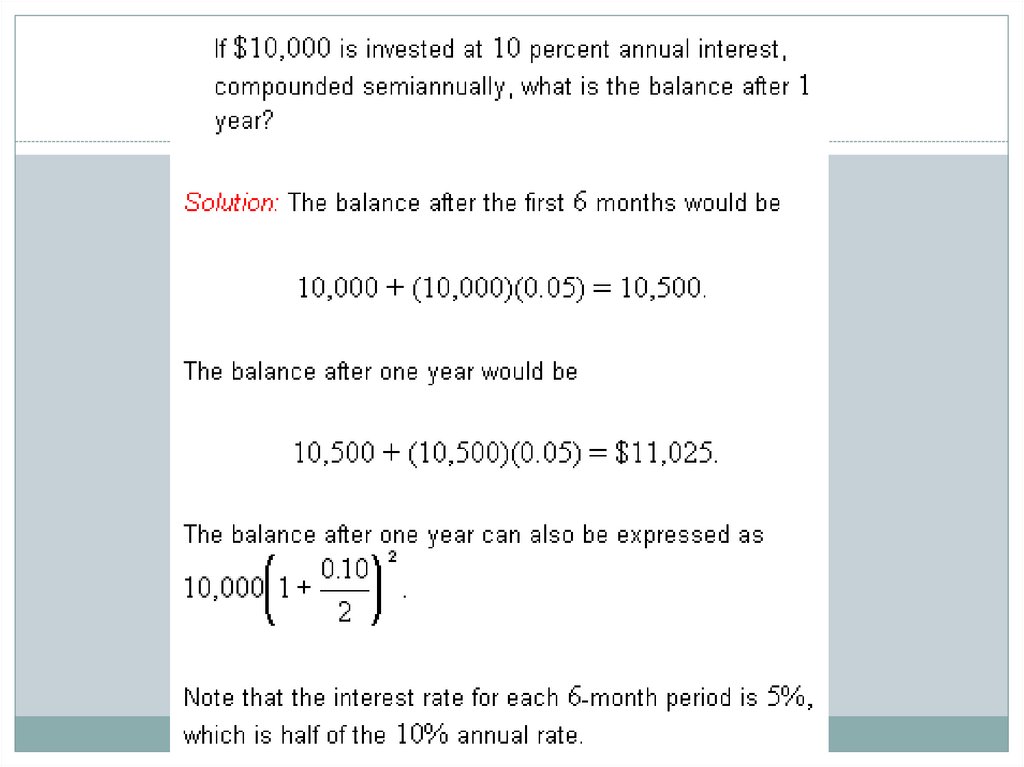
7. D. Interest Problems

8. D. Interest Problems

9. Compound Interest

If a sum of p dollars is invested at an interest rate r
compounded k times a year during n years, the total
amount A (principal and interest) at the end of n
years is equal to
A = p(1+r/k)kn

10. E. Mixture

There are two kinds of mixture problems with which
you could be familiar. The first is sometimes referred
to as dry mixture, in which we mix dry ingredients of
different values, such as nuts or coffee. Also solved by
the same method are problems such as those dealing
with tickets at different prices. In solving this type of
problems, it is best to organize the data in a chart of
three rows and three columns labeled as illustrated in
the following problem.

11. E. Mixture

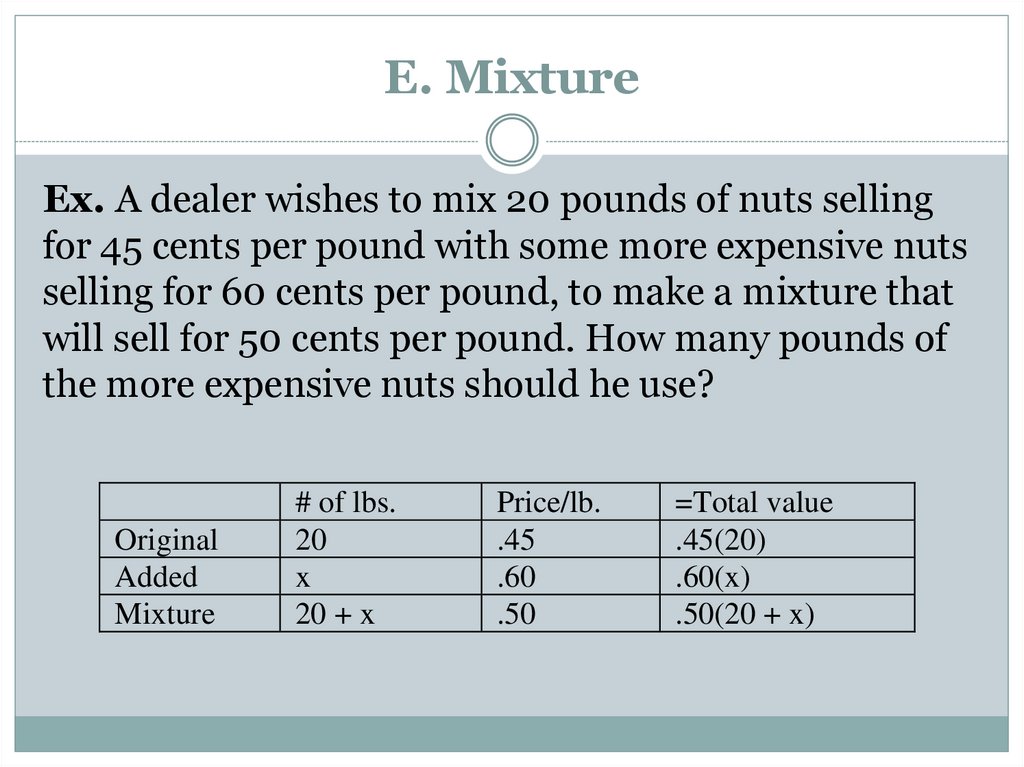
Ex. A dealer wishes to mix 20 pounds of nuts selling
for 45 cents per pound with some more expensive nuts
selling for 60 cents per pound, to make a mixture that
will sell for 50 cents per pound. How many pounds of
the more expensive nuts should he use?

12. E. Mixture

Ex. A dealer wishes to mix 20 pounds of nuts selling
for 45 cents per pound with some more expensive nuts
selling for 60 cents per pound, to make a mixture that
will sell for 50 cents per pound. How many pounds of
the more expensive nuts should he use?
Original
Added
Mixture
# of lbs.
20
x
20 + x
Price/lb.
.45
.60
.50
=Total value
.45(20)
.60(x)
.50(20 + x)

13. E. Mixture

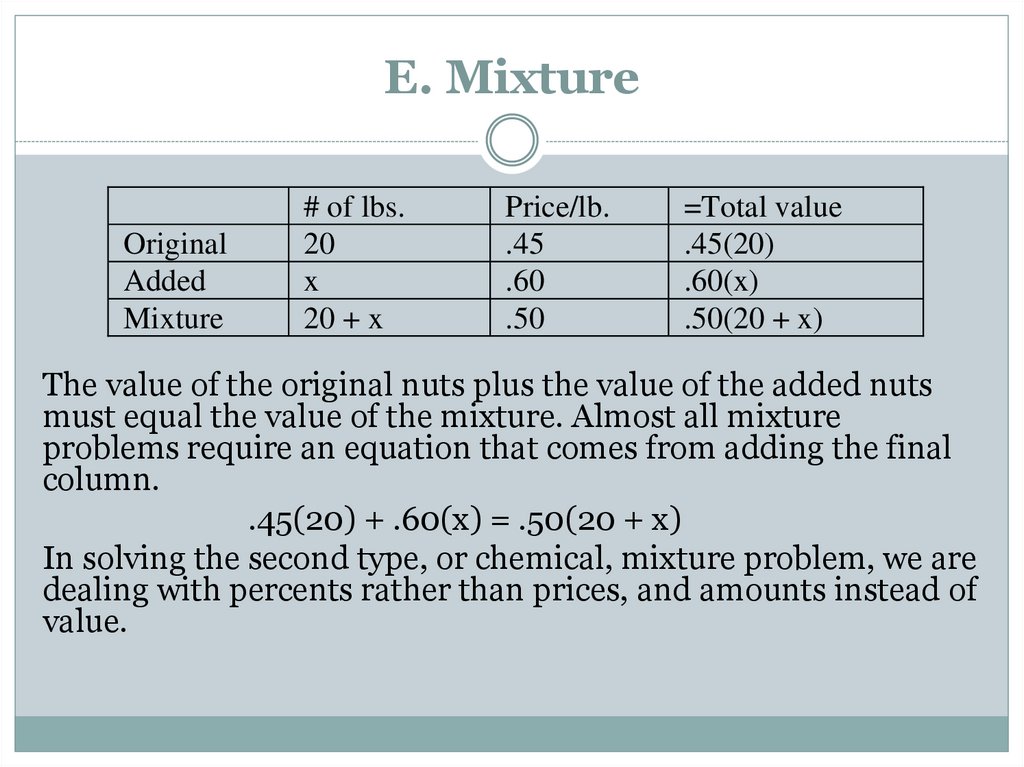
Original
Added
Mixture
# of lbs.
20
x
20 + x
Price/lb.
.45
.60
.50
=Total value
.45(20)
.60(x)
.50(20 + x)
The value of the original nuts plus the value of the added nuts
must equal the value of the mixture. Almost all mixture
problems require an equation that comes from adding the final
column.
.45(20) + .60(x) = .50(20 + x)
In solving the second type, or chemical, mixture problem, we are
dealing with percents rather than prices, and amounts instead of
value.

14. E. Mixture

Ex. How much water must be added to 20 gallons of
solution that is 30% alcohol to dilute it to a solution
that is only 25% alcohol?
Original
Added
Mixture
# of gals.
20
x
20 + x
% alcohol
.30
0
.25
=Amount alcohol
.30 (20)
0
.25 (20 + x)

15. E. Mixture

Original
Added
Mixture
# of gals.
20
x
20 + x
% alcohol
.30
0
.25
=Amount alcohol
.30 (20)
0
.25 (20 + x)
Note that the percent of alcohol in water is 0. Had we added
pure alcohol to strengthen the solution, the percent would
have been 100. The equation again comes from the last
column. The amount of alcohol added (non in this case) plus
the amount we had to start with must equal the amount of
alcohol in the new solution. .30 (20) = .25 (20 + x)

16. E. Mixture

17. E. Mixture

18. E. Mixture

19. E. Mixture

20. F. Motion Problems

The fundamental relationship in all motion problems is that
Rate Time Distance
Most problems fall into one of three types.
Motion in opposite directions. When two objects start at the
same time and move in opposite directions, or when two objects
start at points at a given distance apart and move toward each
other until they meet.
Motion in the same directions. This type of problem is
sometimes called the “catch-up” problem. Two objects leave the
same place at different times and different rates, but one
“catches-up” to the other. In such a case, the two distances must
be equal.
Round trip. In this type of problem, the rate going is usually
different from the rate returning. The times are also different.
But if we go somewhere and then return to the starting point, the
distances must be the same.

21. F. Motion Problems

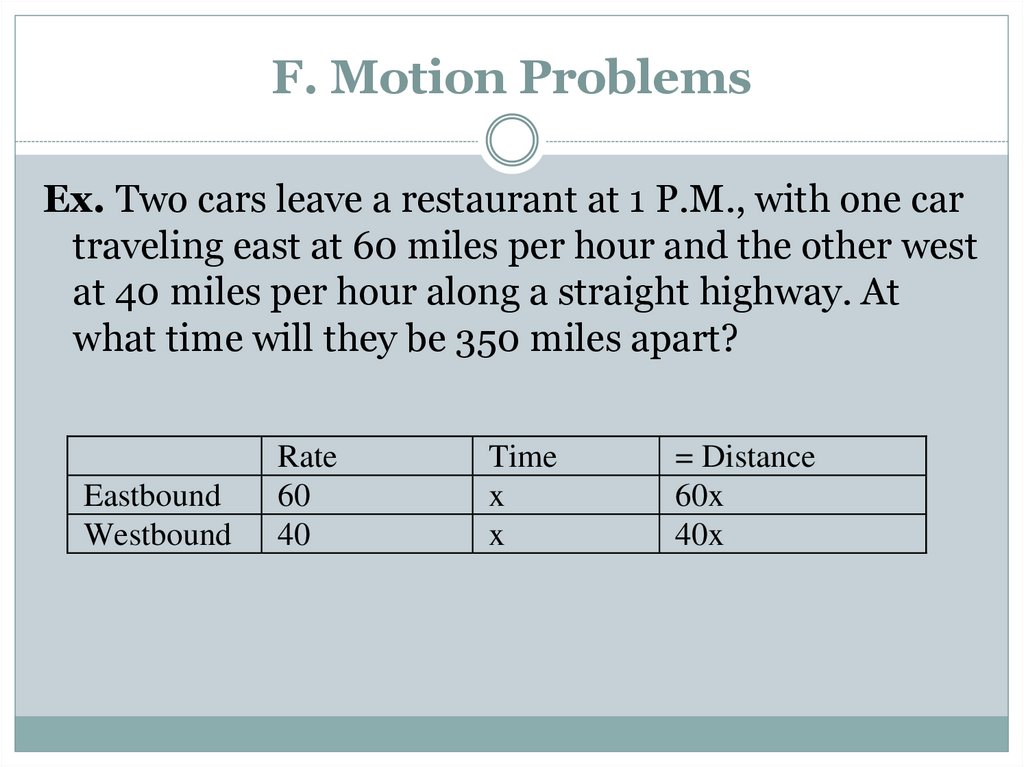
Ex. Two cars leave a restaurant at 1 P.M., with one car
traveling east at 60 miles per hour and the other west
at 40 miles per hour along a straight highway. At
what time will they be 350 miles apart?
Eastbound
Westbound
Rate
60
40
Time
x
x
= Distance
60x
40x

22. F. Motion Problems

Ex. Gloria leaves home for school, riding her bicycle at
a rate of 12 m.p.h. Twenty minutes after she leaves,
her mother sees Gloria’s English paper on her bed
and leaves to bring it to her. If her mother drives at
36 m.p.h., how far must she drive befor she reaches
Gloria?
Gloria
Mother
Rate
12
36
Time
x
x – 1/3
= Distance
12x
36(x – 1/3)

23. F. Motion Problems

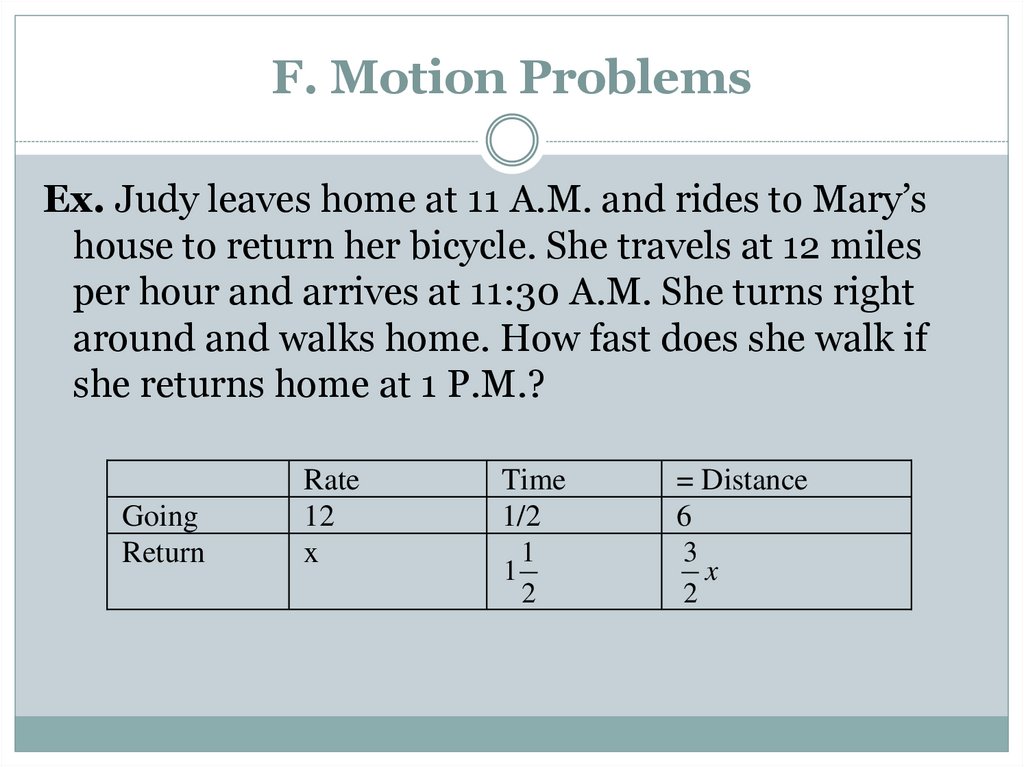
Ex. Judy leaves home at 11 A.M. and rides to Mary’s
house to return her bicycle. She travels at 12 miles
per hour and arrives at 11:30 A.M. She turns right
around and walks home. How fast does she walk if
she returns home at 1 P.M.?
Going
Return
Rate
12
x
Time
1/2
= Distance
6
1
2
3
x
2
1

24. F. Motion Problems

25. F. Motion Problems

26. F. Motion Problems

Average Speed

27. F. Motion Problems

28. G. Work Problems

In most work problems a complete job is broken into
several parts, each representing a fractional part of the
entire job. For each fractional part, which represents the
portion completed by one man, one machine, one pipe,
etc. the numerator should represent the time actually
spent working, while the denominator should represent
the total time needed to do the entire job alone. The sum
of all the individual fractions should be 1.
Ex. Jon can wax his car in 3 hours. Jim can do the same
job in 5 hours. How long will it take them if they work
together?

29. G. Work Problems

30. G. Work Problems

31. G. Work Problems

32. G. Work Problems

33. G. Work Problems

34. Discount

If a price is discounted by n percent, the price
becomes (100 - n) percent of the original price.

35. Discount

If a price is discounted by n percent, the price
becomes (100 - n) percent of the original price.

36. Discount

If a price is discounted by n percent, the price
becomes (100 - n) percent of the original price.

37. Discount

If a price is discounted by n percent, the price
becomes (100 - n) percent of the original price.

38. Profit

Gross profit is equal to revenues minus expenses, or
selling price minus cost.
Example:
A certain appliance costs a merchant $30. At what
price should the merchant sell the appliance in order
to make a gross profit of 50 percent of the cost of the
appliance?
Solution: If s is the selling price of the appliance, then
s - 30 = (0.5)(30), or s = $45.
The merchant should sell the appliance for $45.

39. Sets

If S is the set of numbers 1, 2, 3, and 4, you can write
S = {1,2,3,4}. Sets can also be represented by Venn
diagrams. That is, the relationship among the
members of sets can be represented by circles.

40. Sets

Example 1

41. Sets

42.

43.

44. r

45. V