Похожие презентации:
Математический анализ
1.
Дистанционный курс высшей математикиНИЯУ МИФИ
Математический анализ
1 семестр
Лекция 13
Длина кривой.
Касательная и кривизна.
Приближенные методы
решения уравнений.
11 декабря 2014 года
Лектор: Профессор НИЯУ МИФИ, д.ф.-м.н.
Орловский Дмитрий Германович
2.
Длина кривойx f1 (t ),
y f 2 (t ),
z f (t )
3
t
Если функции f1(t), f2(t), f3(t)
непрерывно дифференцируемы,
то кривая L называется гладкой
кривой (кривая класса С1).
Условие регулярности
[ f1 '(t )]2 [ f 2 '(t )]2 [ f 3 '(t )]2 0
для спрямляемости кривой не обязательно.
3.
Длина кривойТеорема. Гладкая кривая спрямляема и ее длина удовлетворяет
неравенствам
m12 m22 m32 ( ) | L | M12 M 22 M 32 ( ),
где
m j Inf | f j ' (t ) |, (1 j 3),
[ ; ]
M j Sup | f j ' (t ) |, (1 j 3).
[ ; ]
4.
Длина кривойРассмотрим гладкую кривую
L {( x; y; z ) : x f1 (t ), y f 2 (t ), z f 3 (t ), t }
( f1 (t ), f 2 (t ), f 3 (t ) C 1[ ; ]).
Пусть
M (t ) ( f1 (t ); f 2 (t ); f 3 (t ))
( A M ( ), B M ( )).
l (t ) | AM (t ) |
Теорема. Для любой гладкой кривой
l ' (t ) [ f1 ' (t )]2 [ f 2 ' (t )]2 [ f3 ' (t )]2 .
M (t )
5.
Длина кривойДоказательство. Пусть t>t0, тогда по теореме об аддитивности длины
l (t ) l (t0 ) | M (t0 ) M (t ) |
Согласно предыдущей теореме для отрезка [t0;t]
m12 m22 m32 (t t0 ) l (t ) l (t0 ) M12 M 22 M 32 (t t0 )
l (t ) l (t0 )
M 12 M 22 M 32
t t0
mi | f i ' (ξ i ) |, t 0 ξ i t , 1 i 3,
m12 m22 m32
M i | f i ' (ηi ) |, t 0 ηi t , 1 i 3.
lim ξ i lim ηi t0 lim | fi ' (ξ i ) | lim | fi ' (ηi ) | | fi ' (t0 ) | .
t t0
t t0
t t0
t t0
l (t ) l (t0 )
lim
[ f1 ' (t0 )]2 [ f 2 ' (t0 )]2 [ f 3 ' (t0 )]2
t t 0 0
t t0
6.
Длина кривойЕсли t<t0, тогда
l (t0 ) l (t ) | M (t )M (t0 ) |
Согласно предыдущей теореме для отрезка [t; t0]
m12 m22 m32 (t0 t ) l (t0 ) l (t ) M12 M 22 M 32 (t0 t )
l (t0 ) l (t )
M 12 M 22 M 32
t0 t
mi | f i ' (ξ i ) |, t ξ i t 0 , 1 i 3,
m12 m22 m32
M i | f i ' (ηi ) |, t ηi t 0 , 1 i 3.
lim ξ i lim ηi t0 lim | fi ' (ξ i ) | lim | fi ' (ηi ) | | fi ' (t0 ) | .
t t0
t t0
t t0
t t0
l (t ) l (t0 )
l (t0 ) l (t )
lim
lim
[ f1 ' (t0 )]2 [ f 2 ' (t0 )]2 [ f 3 ' (t0 )]2
t t 0 0
t t 0 0
t t0
t0 t
7.
Длина кривойl (t ) l (t0 )
[ f1 ' (t0 )]2 [ f 2 ' (t0 )]2 [ f 3 ' (t0 )]2
t t 0 0
t t0
lim
l (t ) l (t0 )
lim
[ f1 ' (t0 )]2 [ f 2 ' (t0 )]2 [ f 3 ' (t0 )]2
t t 0 0
t t0
Отсюда следует, что
l ' (t ) lim
t t 0
l (t ) l (t0 )
[ f1 ' (t0 )]2 [ f 2 ' (t0 )]2 [ f 3 ' (t0 )]2
t t0
8.
Длина кривойЭлемент длины дуги
Определение. Модуль дифференциала длины дуги называется
элементом длины дуги.
ds | l ' (t )dt | [ f1 ' (t )]2 [ f 2 ' (t )]2 [ f 3 ' (t )]2 | dt | (dx) 2 (dy) 2 (dz) 2
(теорема Пифагора в дифференциалах).
Особенно наглядное значение эта формула имеет для плоской
кривой, являющейся графиком явно заданной функции y=f(x).
График явно заданной функции всегда можно представить в
параметрической форме. Для этого достаточно взять в качестве
параметра независимую переменную.
9.
Длина кривойx t,
y f (t ),
z 0.
ds [ x' (t )]2 [ y ' (t )]2 [ z ' (t )]2 | dt |
1 [ f ' (t )]2 0 | dt | 1 [ f ' ( x)]2 | dx |
( dx) 2 (dy ) 2
ds (dx) 2 (dy ) 2
10.
Касательная к кривойx f1 (t ),
y f 2 (t ),
z f (t ).
3
11.
Касательная к кривойПредельное значение этого вектора при t→t0
a { f1 ' (t0 ); f 2 ' (t0 ); f 3 ' (t0 )}
(в том случае, когда оно отлично от нулевого вектора) называется
касательным вектором к кривой в точке t0.
Прямая, проходящая через точку M(t0) с этим направляющим
вектором, называется касательной к кривой в точке t0.
12.
Касательная к кривойОсобые и регулярные точки кривой
x f1 (t ),
y f 2 (t ),
z f (t ).
3
[ f1 ' (t )] [ f 2 ' (t )] [ f 3 ' (t )] 0 регулярная точка
2
2
2
[ f1 ' (t )] [ f 2 ' (t )] [ f 3 ' (t )] 0 особая точка
2
2
2
В регулярной точке кривая всегда имеет касательную.
13.
Касательная к кривойПример 1.
x t 3 ,
3
y t ,
z 0.
Пример 2.
x t | t |,
2
y
t
,
z 0.
14.
Кривизна плоской кривойСредняя кривизна на участке:
k ср |
s
|
Кривизна в точке M(t0):
k lim kср lim
t t 0
t t 0
| |
s
15.
Кривизна плоской кривойТеорема. Пусть на плоскости задана гладкая регулярная кривая
x (t ),
y (t ).
Тогда ее кривизна в каждой точке t0 определяется формулой
k
| ' (t0 ) ' ' (t0 ) ' ' (t0 ) ' (t0 ) |
(| ' (t0 ) |2 | ' (t0 ) |2 )3 / 2
Замечание.
Гладкая:
, C 1
Регулярная:
| ' (t ) |2 | ' (t ) |2 0
16.
Кривизна плоской кривойДоказательство. Так как кривая регулярна, то величина
| ' (t ) |2 | ' (t ) |2 0
Пусть для определенности
' (t ) 0
Касательный вектор к кривой
a { ' (t ); ' (t )}
образует с осью абсцисс угол
' (t )
arctg
' (t )
17.
Кривизна плоской кривойПо определению кривизны
(t ) (t0 )
k lim
lim
t t0 s
t t0 s ( t ) s ( t )
0
( (t ) (t0 )) / (t t0 )
lim
t t0 ( s ( t ) s ( t )) / ( t t )
0
0
lim( (t ) (t0 )) / (t t0 )
t t0
lim( s(t ) s(t0 )) / (t t0 )
t t0
'(t0 )
s '(t0 )
18.
Кривизна плоской кривойТак как
' (t ) (arctg
' (t )
1
' (t )
)'
(
)'
2
' (t )
1 ( ' (t ) / ' (t )) ' (t )
[ ' (t )]2
' ' (t ) ' (t ) ' (t ) ' ' (t ) ' (t ) ' ' (t ) ' ' (t ) ' (t )
2
2
2
[ ' (t )] [ ' (t )]
[ ' (t )]
[ ' (t )]2 [ ' (t )]2
s' (t ) [ ' (t )]2 [ ' (t )]2 ([ ' (t )]2 [ ' (t )]2 )1/ 2
то
k
'(t ) ''(t ) ''(t ) '(t )
2
2 1/2
/
([
'(
t
)]
[
'(
t
)]
)
2
2
[ '(t )] [ '(t )]
| '(t ) ''(t ) ''(t ) '( t ) |
(| '(t ) |2 | '(t ) |2 ) 3/2
19.
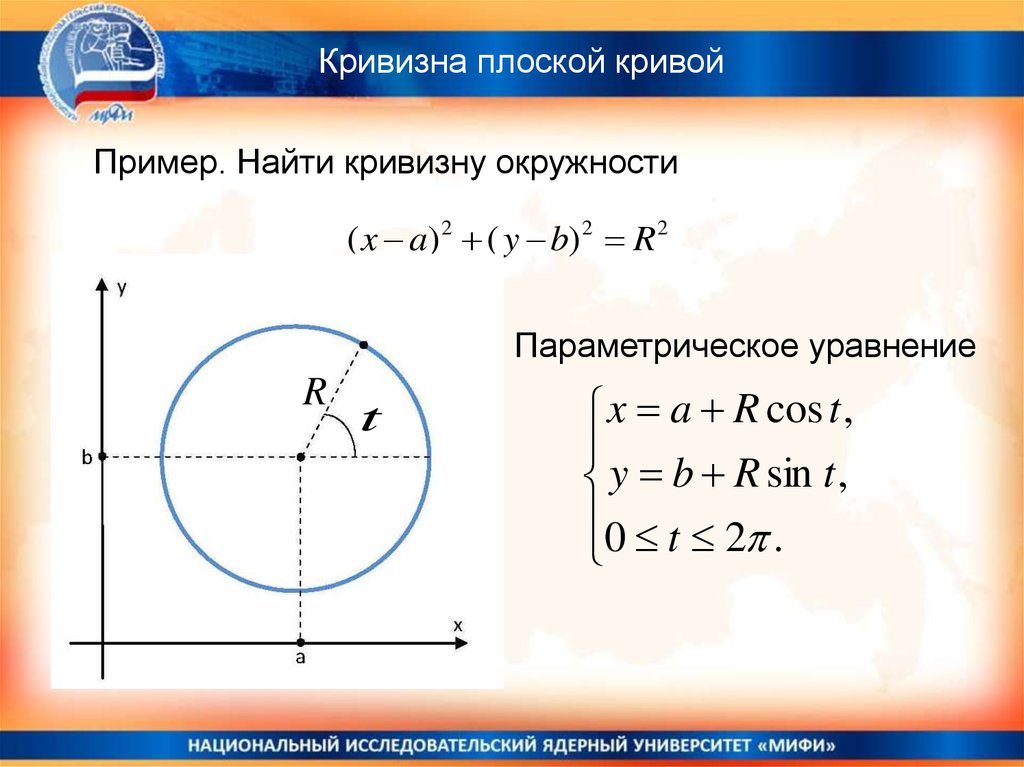
Кривизна плоской кривойПример. Найти кривизну окружности
( x a) 2 ( y b) 2 R 2
Параметрическое уравнение
R
t
x a R cos t ,
y b R sin t ,
0 t 2 .
20.
Кривизна плоской кривой| ' (t ) ' ' (t ) ' ' (t ) ' (t ) |
k
(| ' (t ) |2 | ' (t ) |2 )3 / 2
(t ) a R cos t , (t ) b R sin t
' (t ) R sin t , ' (t ) R cos t
' ' (t ) R cos t , ' (t ) R sin t
' (t ) ' ' (t ) ' ' (t ) ' (t ) ( R sin t )( R sin t ) ( R cos t )( R cos t ) R 2
| ' (t ) |2 | ' (t ) |2 R 2 sin 2 t R 2 cos 2 t R 2
R2
R2 1
k 2 3/ 2 3
(R )
R
R
21.
Кривизна плоской кривойЧасто представляется удобным приближенно заменять кривую
вблизи рассматриваемой точки – окружностью, имеющую ту же
кривизну, что и кривая в данной точке.
Кругом кривизны кривой в данной точке M называется круг,
который
1) касается кривой в точке M;
2) направлен выпуклостью вблизи этой точки в ту же сторону, что
и кривая;
3) имеет ту же кривизну, что и кривая в точке M.
Центр круга кривизны называется центром кривизны, а радиус
этого круга – радиусом кривизны (в данной точке). Для радиуса
кривизны, очевидно, имеем формулу
1
R
k
(k кривизна кривой )
22.
Кривизна плоской кривойЕсли кривая задана в параметрической форме
x (t ),
y (t ),
то координаты центра кривизны кривой в точке (x,y) равны
[ ' (t )]2 [ ' (t )]2
' (t ),
ξ x
' (t ) ' ' (t ) ' ' (t ) ' (t )
2
2
y [ ' (t )] [ ' (t )]
' (t ).
' (t ) ' ' (t ) ' ' (t ) ' (t )
23.
Кривизна плоской кривойЕсли кривая задана как график явной функции
y f (x),
то параметрическое уравнение этой кривой имеет вид
x t,
y f (t ).
Задача. Показать, что кривизна такой кривой
f ' ' ( x)
k
,
2 3/ 2
(1 [ f ' ( x)] )
а координаты центра кривизны
1 [ f ' ( x)]2
1 [ f ' ( x)]2
ξ x
f ' ( x), y
.
f ' ' ( x)
f ' ' ( x)
24.
Эволюта плоской кривойГеометрическое множество центров кривизны данной кривой
называется ее эволютой. Сама кривая по отношению к своей
эволюте называется эвольвентой.
Пример. Найти эволюту параболы y2=2px.
Дифференцируя уравнение, находим
2 yy ' 2 p; yy ' p,
( y ' ) 2 yy ' ' 0; yy' ' ( y' ) 2 ; y 3 y ' ' ( yy ' ) 2 ; y 3 y ' ' p 2 .
Координаты центра кривизны
1 [ y ' ]2
(1 [ y ' ]2 ) y 2
y2 p2
2 px p 2
3y2
ξ x
y' x
yy ' ( x) x
x
3x p
p,
y' '
y' ' y 3
p
p
2p
1 [ y ' ]2
(1 [ y ' ]2 ) y 2
y2 p2
y2
y
y
y y
y 2.
y' '
y' ' y 3
p2
p
25.
Эволюта плоской кривойИз полученных уравнений
3y2
y2
ξ
p, 2 .
2p
p
Исключаем y и получаем уравнение эволюты
2
8
(ξ p ) 3
27 p
(полукубическая парабола)
26.
Метод итераций (последовательных приближений)x ( x)
Замечание.
f ( x ) 0 x x cf ( x ) x ( x ) ( ( x ) x cf ( x ))
x1 ( x0 )
x2 ( x1 )
xn ( xn 1 )
27.
Метод итерацийПринцип сжимающих отображений
Пусть выполнены следующие условия
(1) x [a, b] ( x ) [a, b],
(2) q (0,1) x, y [a, b] | ( x ) ( y ) | q | x y | .
Тогда на отрезке [a,b] существует и притом единственное
решение уравнения
x ( x ).
При этом метод итераций для x0∊[a,b] дает последовательность,
сходящуюся к решению этого уравнения. Более того
qn
| xn x |
| ( x0 ) x0 | .
1 q
28.
Метод итерацийДоказательство. В силу условия (1) последовательность итераций
определена. Покажем, что она фундаментальна.
Лемма. При m≥n
| xm xn | q n | xm n x0 |
В самом деле
| xm xn | | ( xm 1 ) ( xn 1 ) | q | xm 1 xn 1 |
Применяя при m≥n полученное неравенство n раз, получаем
| xm xn | q | xm 1 xn 1 | q 2 | xm 2 xn 2 | ... q n | xm n x0 |
Следствие:
| xn 1 xn | q n | x1 x0 |
29.
Метод итерацийОценим, теперь, величину
| xk x0 | | ( xk xk 1 ) ( xk 1 xk 2 ) ... ( x1 x0 ) |
q k 1 | x1 x0 | q k 2 | x1 x0 | ... | x1 x0 |
k
1
q
| x1 x0 |
k 1
k 2
( q q ... 1) | x1 x0 |
| x1 x0 |
.
1 q
1 q
Итак, мы имеем два неравенства
| x1 x0 |
| xm xn | q | xm n x0 |, | xk x0 |
,
1 q
n
Из которых следует, что при m≥n
| x1 x0 |
| xm xn | q
1 q
n
30.
Метод итераций| x1 x0 |
| xm xn | q
(m n )
1 q
n
ε 0
| x1 x0 |
n | x1 x0 |
lim q
0 N n N q
n
1 q
1 q
n
n N , m n | xm xn |
m, n N | xm xn |
31.
Метод итерацийx lim xn
n
(1) a xn b x [a, b]
(2) 0 | ( xn ) ( x ) | q | xn x | ( xn ) ( x)
(3) xn ( xn 1 ) x ( x )
| x1 x0 |
n | x1 x0 |
| xm xn | q
, m | x xn | q
1 q
1 q
| x xn | | xn x |, | x1 x0 | | ( x0 ) x0 |
n
qn
| xn x |
| ( x0 ) x0 |
1 q
32.
Метод итерацийЕдинственность решения.
x ( x ), y ( y )
| x y | | ( x ) ( y ) | q | x y |
(1 q) | x y | 0
| x y | 0
x y
33.
Иоганн КеплерНемецкий математик, астроном и оптик,
27.12.1571 – 15.11.1630 первооткрыватель законов движения планет
Солнечной системы.
В 1591 поступил в университет в Тюбингене, в
1594 приглашен для чтения лекций по
математике в университет города Граца
(Австрия).
На протяжении нескольких лет Кеплер в
результате тщательного анализа приходит к
выводу, что траектория движения Марса
представляет собой не круг, а эллипс, в одном из
фокусов
которого
находится
Солнце
—
положение, известное сегодня как первый закон
Кеплера.
Дальнейший анализ привёл ко второму закону: радиус-вектор,
соединяющий планету и Солнце, в равное время описывает равные
площади. Это означало, что чем дальше планета от Солнца, тем
медленнее она движется.
34.
Иоганн КеплерВ 1612 году Кеплер переезжает в Линц, где прожил 14 лет. За ним
сохранена должность придворного математика и астронома, но в деле
оплаты новый император ничем не лучше старого. Некоторый доход
приносят преподавание математики и гороскопы.
Продолжая астрономические исследования, Кеплер в 1618 году
открывает третий закон: отношение куба среднего удаления планеты от
Солнца к квадрату периода обращения её вокруг Солнца есть величина
постоянная для всех планет: a³/T² = const. Этот результат Кеплер
публикует в завершающей книге «Гармония мира», причём применяет его
уже не только к Марсу, но и ко всем прочим планетам, включая,
естественно, и Землю.
В 1626 году в ходе Тридцатилетней войны Линц осаждён и вскоре
захвачен. Начинаются грабежи и пожары. Кеплер переезжает в Ульм.
В 1630 году отправляется к императору в Регенсбург, чтобы получить
хотя бы часть жалованья. По дороге сильно простужается и вскоре
умирает.
Законы планетной кинематики, открытые Кеплером, послужили позже
Ньютону основой для создания теории тяготения. Ньютон математически
доказал, что все законы Кеплера являются следствиями закона тяготения.
35.
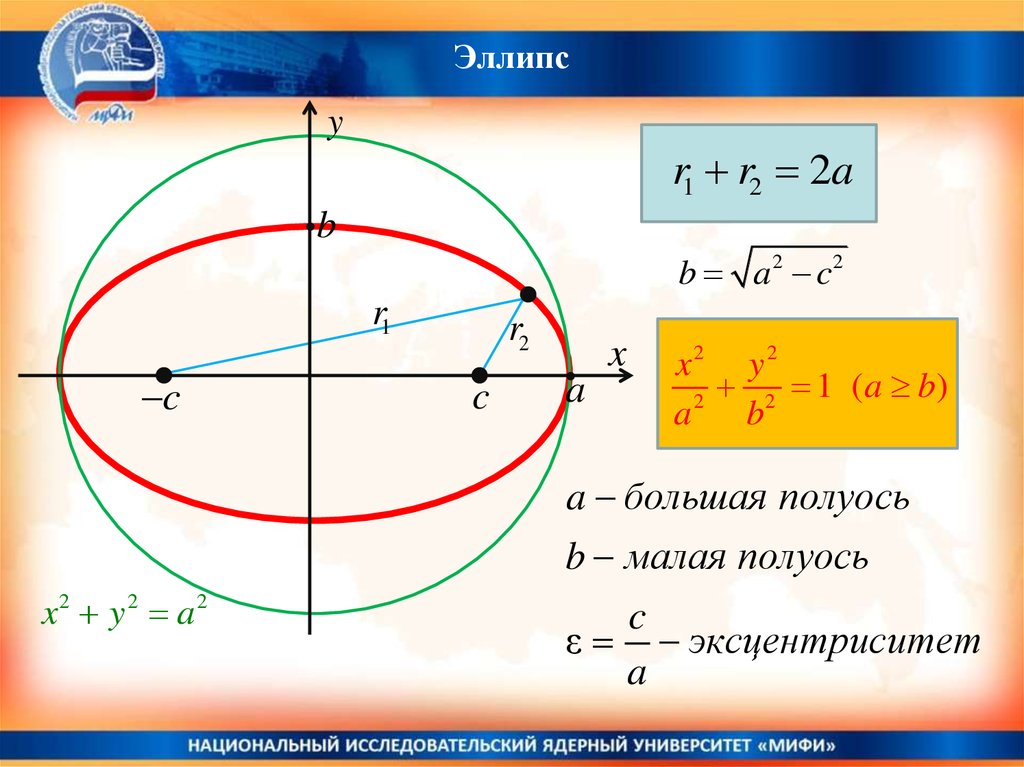
Эллипсy
r1 r2 2a
b
b a 2 c2
r1
c
r2
c
x
a
x2 y2
2 1 ( a b)
2
a
b
a большая полуось
b малая полуось
x2 y 2 a2
c
ε эксцентриситет
a
36.
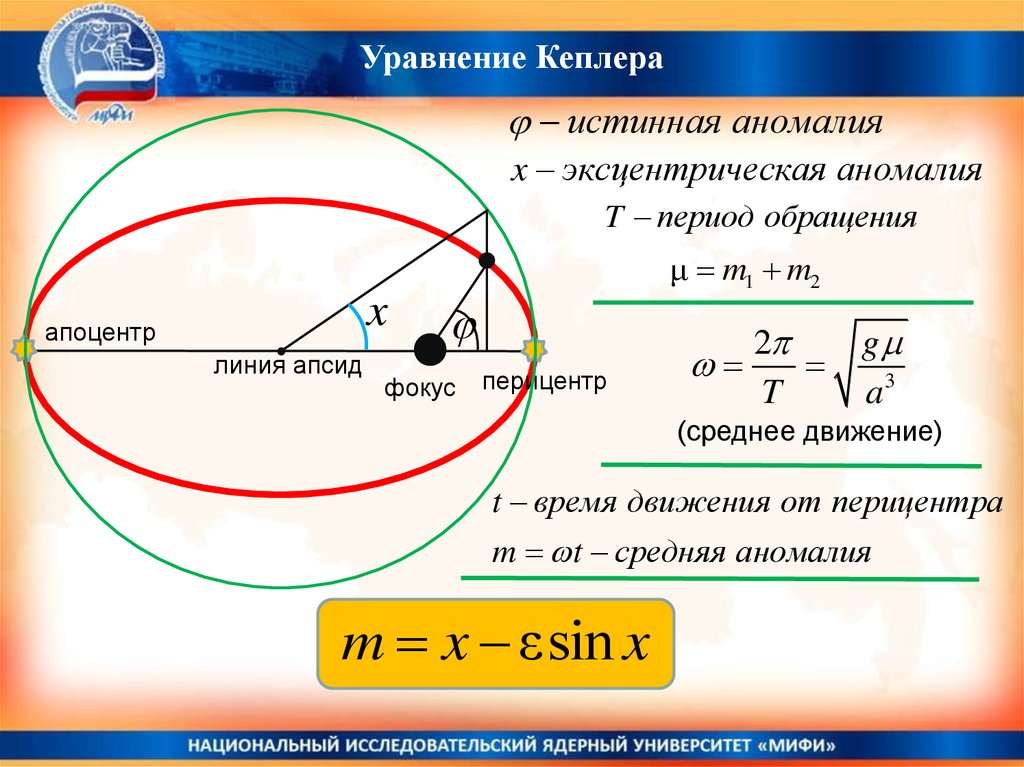
Уравнение Кеплераистинная аномалия
x эксцентрическая аномалия
T период обращения
μ m1 m2
x
апоцентр
линия апсид
фокус
перицентр
2
T
g
a3
(среднее движение)
t время движения от перицентра
m t средняя аномалия
m x εsin x
37.
Метод итераций (пример)Уравнение Кеплера
x m ε sin x (0 ε 1)
( x ) m ε sin x
[a, b] [m 1, m 1]
'( x ) ε cos x | '( x ) | ε
| ( x ) ( y )|=| '(ξ)( x y )| ε|( x y )|
Таким образом, итерации
xn m εsin xn 1
сходятся к единственному решению этого уравнения.
38.
Метод итераций (пример)Оценка погрешности:
1619
εn
| xn x |
| ( x0 ) x0 | .
1 ε
x 2 0,1sin x (с точностью до 0,001)
(0,1)n
m 2 ε 0,1 d
| ( x0 ) x0 |
0,9
x0 2,
d 0,1
x1 2,09093, d 0,01
x2 2,08678, d 0,001
x3 2,08698, d 0,0001
Ответ:
x 2,087
39.
Дистанционный курс высшей математикиНИЯУ МИФИ
Математический анализ.
Приближенные методы
решения уравнений.
Лекция 13
завершена.
Спасибо за внимание!
Тема следующей лекции:
Обзорная лекция.
Лекция состоится в четверг 18 декабря
В 10:00 по Московскому времени.




































 Математика
Математика








