Многокритериальная параметрическая оптимизация систем управления

1. Многокритериальная параметрическая оптимизация систем управления

КУРСОВАЯ
РАБОТА
по дисциплине:
«Проектирование систем управления»
1

2. Задание

Выбрать реальную систему и описать ее работу, приведя
функциональную схему (ФС).
Получить модель выбранной системы (не ниже 3-го
порядка) в виде структурной схемы и описать ее связь с ФС.
Получить переходную функцию (ПФ) исходной системы.
В качестве выходных параметров использовать:
1) перерегулирование и 2) время регулирования.
Обоснованно выбрать варьируемые параметры.
Определить область работоспособности системы.
Использовать в качестве критериев оптимальности:
среднеквадратическую ошибку, выходные параметры
и аддитивный суперкритерий .
2

3. Задание (продолжение)

Оптимизировать исходную систему поочередно по разным
критериям,
обоснованно
используя
в
качестве
инструмента методы параметрической оптимизации.
Получить для каждого из найденных оптимальных
значений варьируемых параметров переходные функции.
Привести графики переходных функций, сравнить их
между собой по внешним параметрам в зависимости от
исследуемых критериев и сделать выводы.
Построить в пространстве критериев множество Парето.
Изобразить внешний вид системы или ее части с
помощью пакета AutoCAD в 3D.
Привести список использованной литературы и webадреса источников информации.
3

4. Описание работы системы стабилизации (СС) самолета по углу тангажа

Гироскопический блок, ось которого направлена вдоль вертикальной оси
самолета, имеет выходной потенциометр, неподвижно закрепленный на
фюзеляже.
При отклонении горизонтальной оси самолета на некоторый угол (угол
тангажа), корпус потенциометра повернется на тот же угол, т.к. гироскоп
стремится сохранить свое положение неизменным.
Выходной потенциометр соединен с задающим потенциометром, при
перемещении ползунка которого в потенциометрической системе образуется
напряжение рассогласования Uп, которое поступает на усилитель. Усилитель
питает двухфазный электродвигатель переменного тока, приводящий в
движение через редуктор золотник гидроусилителя. Гидроусилитель и силовой
поршень цилиндра образуют гидравлическую рулевую машинку.
При смещении золотника поршень цилиндра перемещается и
поворачивает через рычаг руль высоты. С рулем высоты связан потенциометр
обратной связи, с которого снимается напряжение обратной связи Uос,
соответствующее углу поворота руля Uбв.
Самолет под действием руля высоты будет перемещаться до тех пор, пока
его ось не повернется на угол c(t). В этом случае напряжение рассогласования
Uп станет равным нулю, и самолет начнет набирать высоту под заданным углом
4
тангажа.

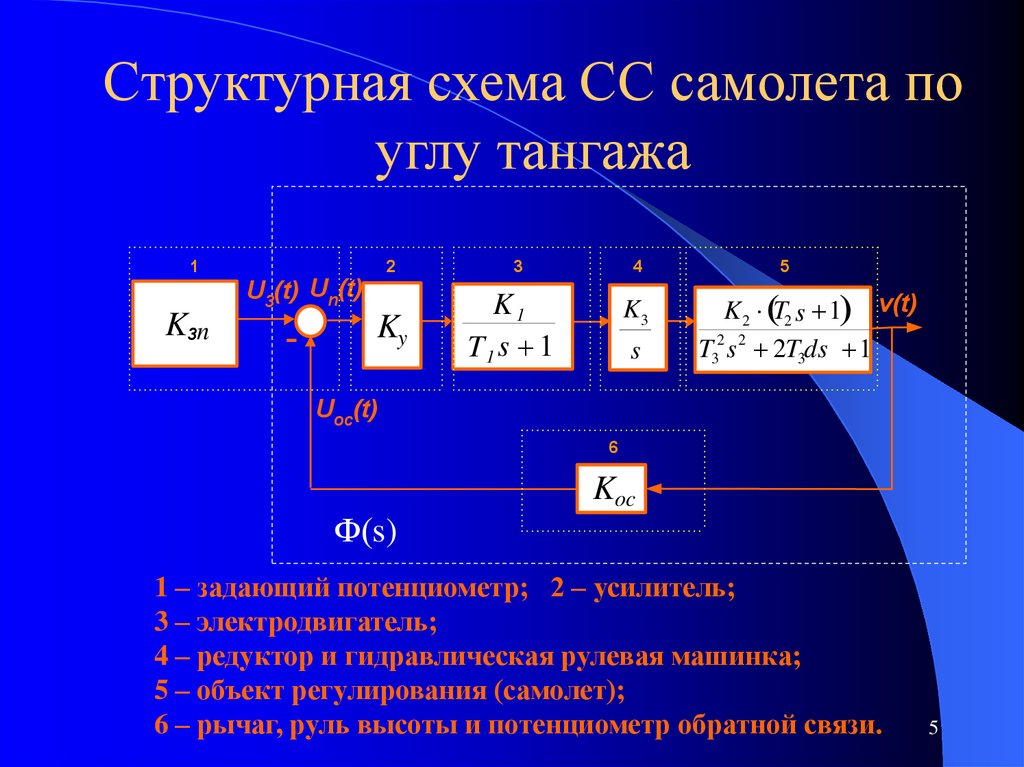
5. Структурная схема СС самолета по углу тангажа

1
2
U3(t) Un(t)
K3n
Ky
ó
3
4
K1
T1 s 1
K3
s
5
K 2 T2 s 1 v(t)
T32 s 2 2T3ds 1
Uoc(t)
6
ËKoc
Ф(s)
1 – задающий потенциометр; 2 – усилитель;
3 – электродвигатель;
4 – редуктор и гидравлическая рулевая машинка;
5 – объект регулирования (самолет);
6 – рычаг, руль высоты и потенциометр обратной связи.
5

6. Модели устройств СС самолета

1.
Задающий потенциометр.
4.
Летательный аппарат.
Передаточная функция потенциометра:
Wп ( s ) К п
,
Wc ( s)
K 2 T2 s 1
T32 s 2 2 T3 s 1
К2
Т2
Т3
0,57
0,33
0,143
где Кп=1 - коэффициент пропорциональности.
2. Усилитель.
Передаточная функция усилителя:
1,0
Wу ( s) К у
,
где Ку - коэффициент усиления.
3.
5.
W р (s)
Двигатель.
Передаточная функция двигателя:
Wдв ( s )
Рулевая машинка.
К1
Т1s 1
где К1=0,157 – коэффициент усиления;
Т1=0,28 - постоянная времени двигателя.
6.
К3
s ,
где К3=30
Потенциометр обратной связи.
Wос ( s) К ос К 4 1
6

7. Выбор варьируемых параметров

В процессе проведения оптимизации данной
системы изменениям следует подвергнуть только
коэффициент усиления Ку.
Другие параметры будут оставаться неизменными,
т.к. их варьирование связано с практическим
неудобством их реального изменения в системе
может повлечь значительные конструктивные
изменения.
Например, выбрав в качестве варьируемого
параметра постоянную времени T1, мы должны
иметь в виду, что это может потребовать изменений
в конструкции или даже замены двигателя и т.п.,
что нецелесообразно.
7

8. Описание модели СС самолета в передаточных функциях

Передаточная функция разомкнутой системы самолета
по углу тангажа с учетом передаточных функций все входящих в
нее устройств будет иметь вид:
W раз ( s)
К п К у К1 К 2 К 3 Т 2 s 1
s T1s 1 T32 s 2 2 T3 s 1
Передаточная функция замкнутой системы с учетом
отрицательной обратной связи с коэффициентом Кос будет
иметь вид:
замк( s)
W раз ( s)
1 W раз ( s) К ос
К Т 2 s 1
,
2 2
s T1s 1 T3 s 2 T3 s 1 K Т 2 s 1
где
К=КпКуК1К2К3.
8

9. Определение области работоспособности

Поскольку условия работоспособности в задании не оговорены,
то будем исходить из самых слабых возможных ограничений.
Таковыми, как известно, являются требования устойчивости:
если система становится неустойчивой – значит она перестает
быть работоспособной.
Поэтому если из условия нахождения системы на границе
устойчивости мы получим ограничения на варьируемые
параметры, то это и позволит, по существу, определить одну из
границ максимально возможной области работоспособности.
Другие границы этой области можно определить из других
разумных условий: например, обеспечения передачи
информационных сигналов между устройствами системы и т.п.
9

10.

Итак, в рассматриваемой системе выбран один варьируемый
параметр: коэффициент усиления Ку, - который входит как
сомножитель в общий коэффициент передачи разомкнутой
системы К.
Для того чтобы составить характеристическое уравнение,
необходимо приравнять знаменатель передаточной
функции замкнутой системы к нулю:
s T2 s 1 T32 s 2 2 T3 s 1 K Т 2 s 1 0
Раскрывая скобки и подставляя числовые значения всех
параметров, кроме К, получаем:
4
3
2
0
,
0057
s
0
,
1005
s
0
,
566
s
1 0,33K s
К 0
a
a4
a3
a2
0
a1
По коэффициентам этого уравнения составим
определитель Гурвица и приравняем его нулю, т.к. это
соответствует границе устойчивости:
4
a3
a1
0
0
a4
a2
a0
0
0
0
a3
a4
a1
a2
0
a0
0,1005 1 0,33K
0
0
0,0057
0,566
К
0
0
0,1005
1 0,33К
0
0
0,0057
0,566
К
Отсюда К = 12,98 , и тогда
0; Ку 12,98
К п К1 К 2 К 3
12,98
4,34
1 0,175 0,57 30
10

11. Пример определения ОРx (продолжение)

При Ку = 4,34 система находится на границе устойчивости,
следовательно при Ку < 4,34 система будет устойчива.
Поскольку варьируемый параметр всего один, то область
работоспособности в этом частном случае представляет собой
отрезок значений на действительной прямой, т.е. диапазон
значений.
Верхнее значение диапазона изменения параметра Ку=4,34.
Нижнее значение диапазона определим из условия обеспечения
передачи
информации
от
устройства
к
устройству:
неразрывности (прямой) цепи. Из этого условия следует, что
коэффициенты передачи всех устройств, в том числе и
усилителя, должны быть больше нуля! Если хотя бы один из них
будет равен нулю, произойдет разрыв цепи, и информация не
пройдет на выход системы.
Исходя из этого нижнее значение диапазона: Ку=0.
В результате получаем диапазон изменения варьируемого
(управляемого) параметра Ку: K (0 ; 4,34) или реально K 0,01 ; 4,3
y
y
11

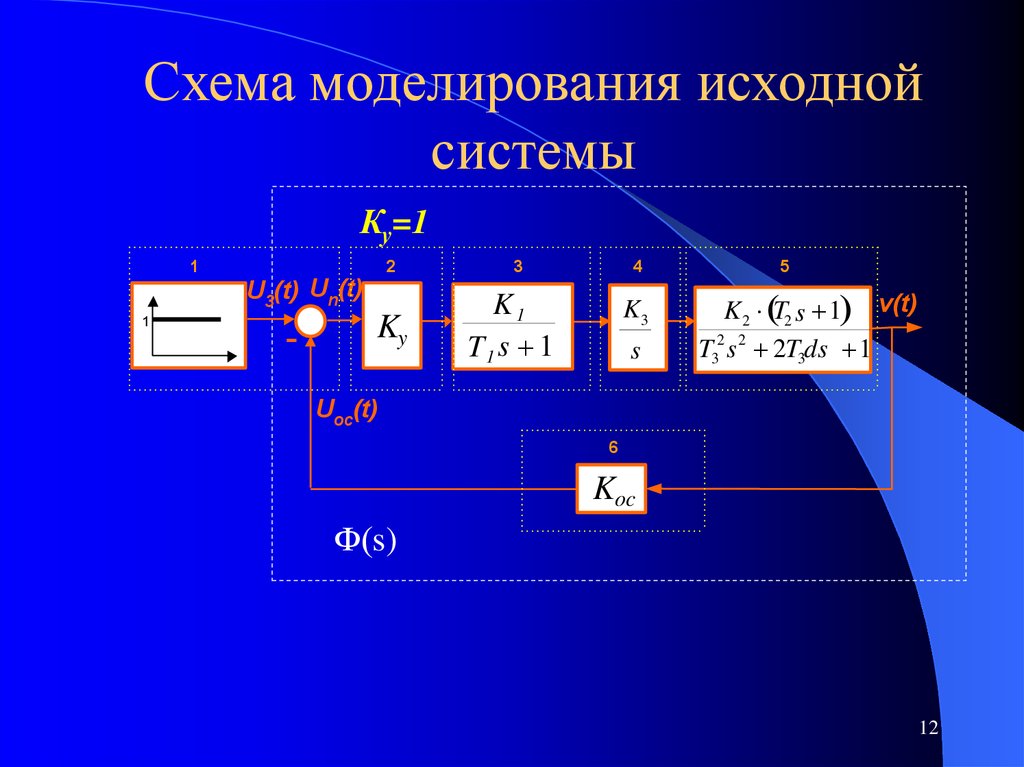
12. Схема моделирования исходной системы

Ку=1
1
2
U3(t) Un(t)
1
Ky
ó
3
4
K1
T1 s 1
K3
s
5
K 2 T2 s 1 v(t)
T32 s 2 2T3ds 1
Uoc(t)
6
ËKoc
Ф(s)
12

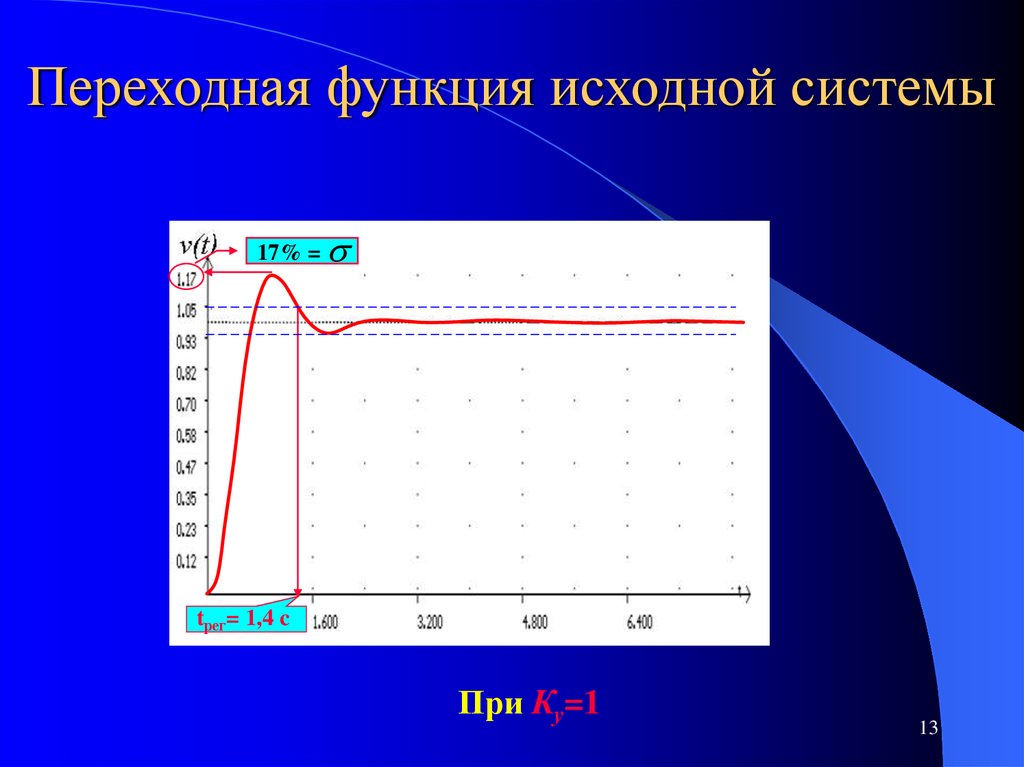
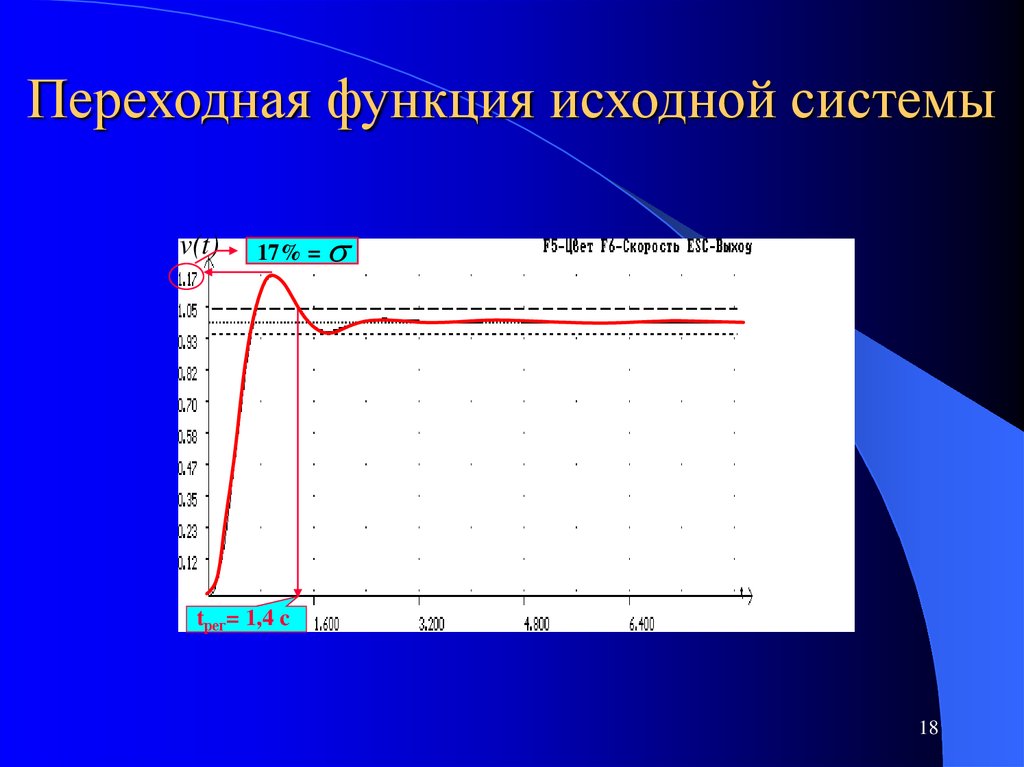
13. Переходная функция исходной системы

17% =
tрег= 1,4 c
При Ку=1
13

14. Переходная функция системы после оптимизации по среднеквадратической ошибке

14

15. Переходная функция СУ после оптимизации по среднеквадратической ошибке

35% =
10% от vуст
vуст=1.00
tрег= 2,3 c
15

16. Переходные функции исходной системы до и после оптимизации по среднеквадратической ошибке

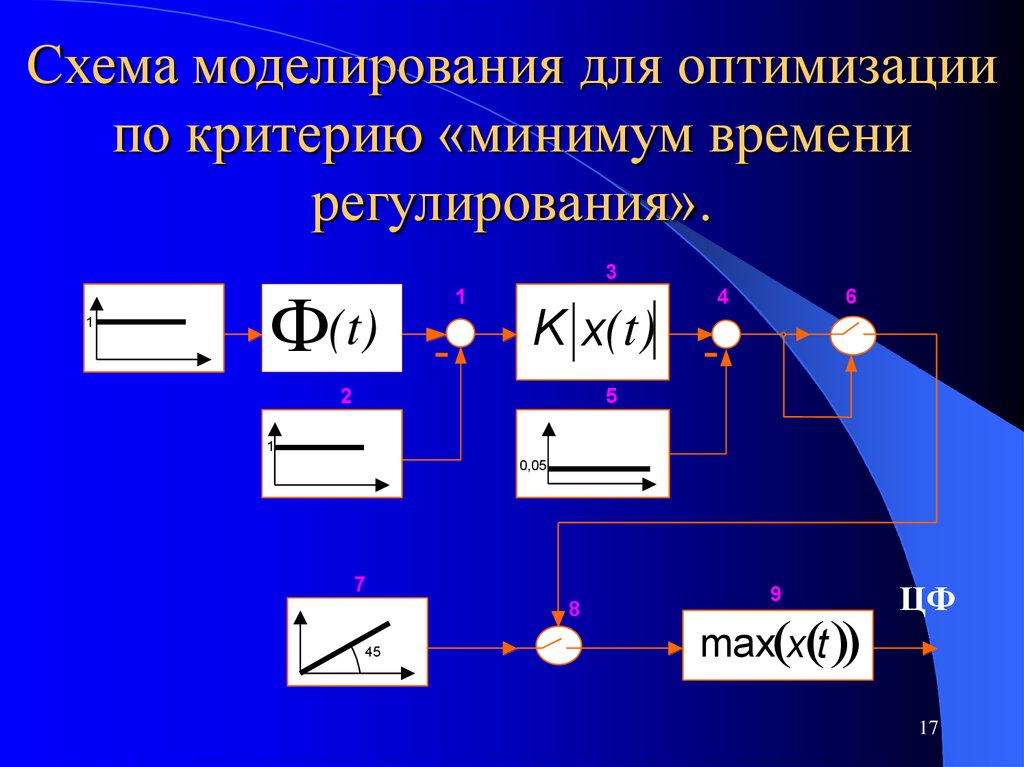
16

17. Схема моделирования для оптимизации по критерию «минимум времени регулирования».

1
(t)
3
1
4
6
K x(t)
2
5
1
0,05
7
8
45
9
max x t
ЦФ
17

18. Переходная функция исходной системы

v(t)
www
17% =
tрег= 1,4 c
18

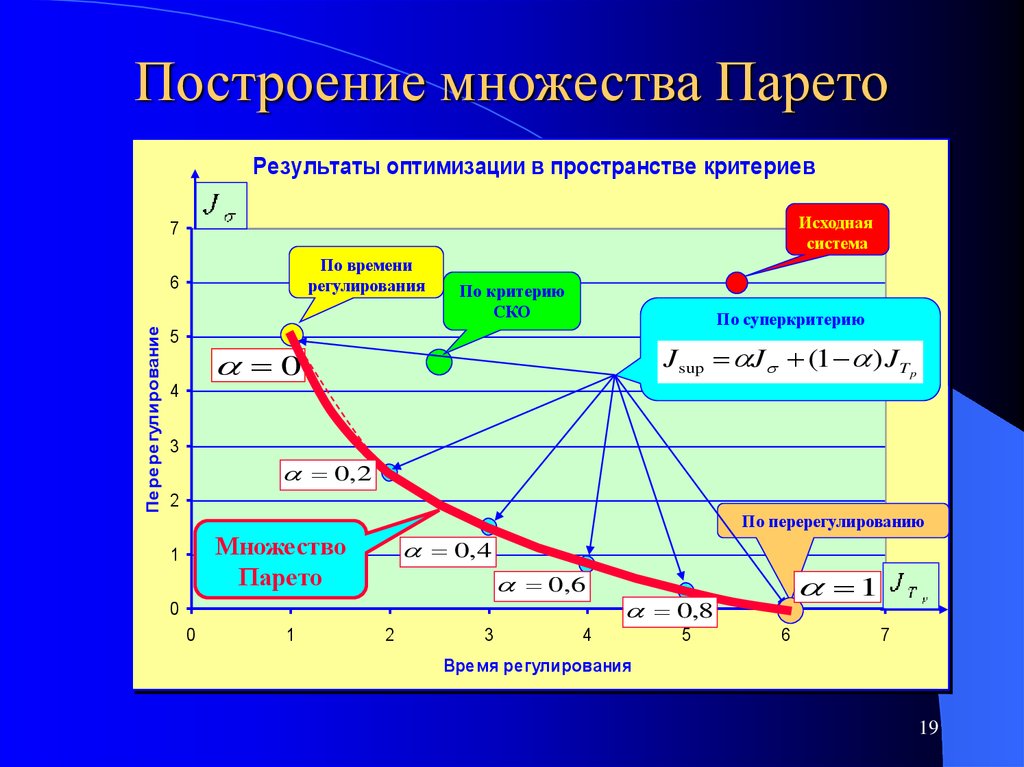
19.

Построение множества Парето
Результаты оптимизации в пространстве критериев
Исходная
система
7
По времени
регулирования
Перерегулирование
6
5
По критерию
СКО
По суперкритерию
J sup J (1 ) JTp
0
4
3
0,2
2
По перерегулированию
Множество
Парето
1
0,4
0,6
0
0
1
2
3
1
0,8
4
5
6
7
Время регулирования
19