Спин – орбитальная связь

1. Квантовая и ядерная физика Раздел АТОМ. Многоэлектронные атомы. Спин – орбитальная связь

Абрик Ибрагимович Валишев, к.ф. - м.н., профессор
? Марлен Еновкович Топчиян , д.ф. -м.н., профессор

2. ЛЕКЦИЯ 17. Спин – орбитальная связь.

А.И. Валишев

3. Механизмы взаимодействия в многоэлектронном атоме.

4. Виды взаимодействий

Виды взаимодействий в многоэлектронном
атоме
Помимо кулоновского взаимодействия
электронов с ядром имеется:
1. Кулоновское межэлектронное
взаимодействие.
2. Магнитное взаимодействие электронных
токов
Экспериментальные данные: определяющим
является электростатическое
взаимодействие.
Вырождение в кулоновском центральном поле 1/r
снимается учетом межэлектронного
взаимодействия

5. Метод самосогласованного поля.

6. Метод самосогласованного поля. МССП

Попарное взаимодействие электронов
учитывается как эффективное взаимодействие
единственного электрона с осредненным
центральным кулоновским полем остальных Z-1
электронов
Hˆ CCП
2
N
N
1
e
1
0
hˆ hˆi V ik
2 i k rik i 1
2 i k
i 1
N
N
0
i
Энергия основного
из
состояния :
условия минимума вариации функионала
ˆ
H CCP 0

7. Метод самосогласованного поля. МССП

В отсутствии межэлектронного
взаимодействия:
h – одноэлектронный потенциал i – го состояния.
- многоэлектронная ВФ (волновая функция
Хартри)
2
2
pˆ i Ze
0
ˆ
hi
2m ri
a ( 1) k 1 ( r1 ) k 2 ( r2 ) kN ( rN )
Результат.
1. Потенциал самосогласованного поля
сферически симметричный потенциал V(r)
2. V(r < a) ~ - Ze2/r, на малых расстояниях
V(r >> a) ~ - e2/r – на больших

8. Метод самосогласованного поля. МССП

-(Z-1)e
-e
+(Z)e
Отношение энергии взаимодействия всех пар электронов (всего пар
Z(Z-1)/2 штук) к полной энергии взаимодействия электронов с ядром
при одинаковом характерном расстоянии между зарядами:
1
Z ( Z 1)
2
W
1 1
i , j Z ( Z 1) / 2 e / r 2
,
2
2
Z Ze / r
Z
4 2
WN

9. Метод самосогласованного поля. МССП

V (r )
Вид «самосогласованного» потенциала:
r
2
e
r
Ze
r
2

10. Метод самосогласованного поля. МССП

Результат.
3. Кулоновское вырождение по орбитальному
моменту и проекции момента снимается.
В силу сферической симметрии потенциала
остается вырождение только по проекции
орбитального момента lz
Энергия уровня в атоме становится зависимой
от главного квантового числа n и значения
орбитального момента l
E En ,l

11. Спин – орбитальное взаимодействие.

12. Приближение LS связи

Спин – орбитальное взаимодействие
приближенно моделируется взаимодействием
полного орбитального магнитного момента
атома (магнитный момент помещен в центре
атома) и полного спинового магнитного
момента (находящегося на расстоянии
Боровского радиуса) – аналог электрического
диполь-дипольного взаимодействия
Классическая модель:
Рассмотрение орбитального движения ядра в
системе отсчета электрона. «Ядерным»
орбитальным электрическим током создается
магнитное поле B, взаимодействующее со
спиновым магнитным моментом электрона S

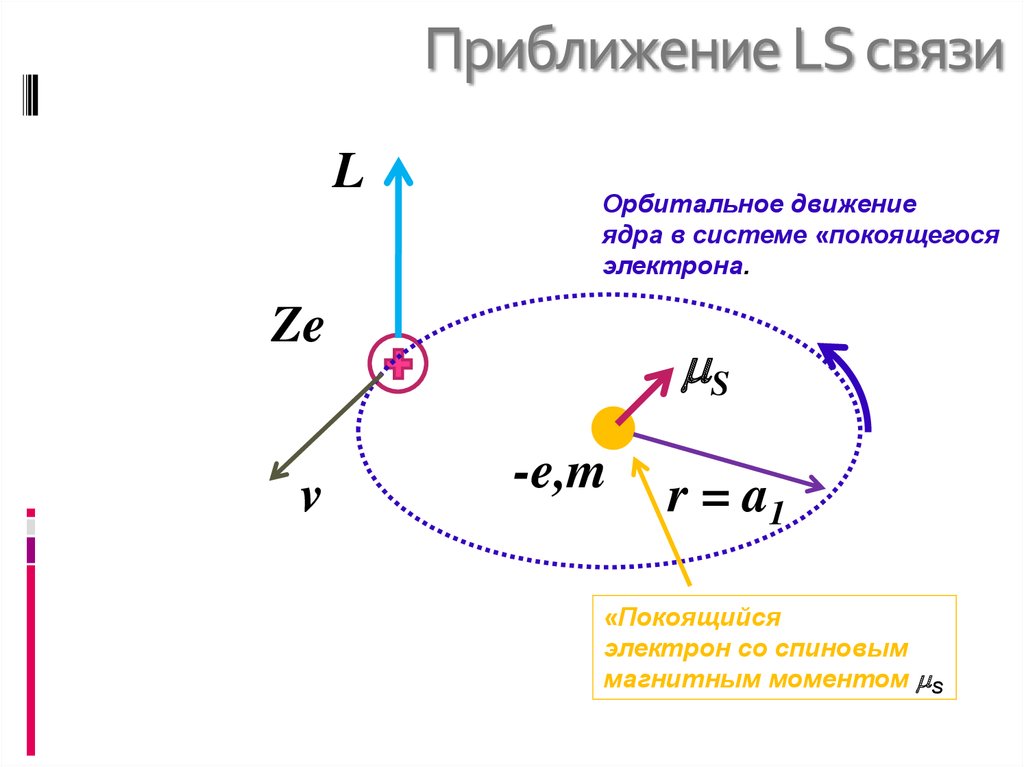
13. Приближение LS связи

L
Орбитальное движение
ядра в системе «покоящегося
электрона.
Ze
v
S
-e,m
r = a1
«Покоящийся
электрон со спиновым
магнитным моментом S

14. Приближение LS связи

q Ze
Ep
r,
Эл. поле протона в системе CGSE
3
r
" Орбитальное" движение Z протонов
создает индукцию магнитгого поля B :
[v E ]
q
( q Ze)
B
me [ v r ]
L,
3
3
c
me c r
me c r
Поправка к энергии :
VS ,L
1 me Z 2 e 4
1
Ze2
B 2 2 3 LS
2 me c r
2 2
Введены :
2
a1
,
2
Zme e
e
S
S,
me c
Z e 1 L S
3 3 6 2 2 3
2
Z me e c r
6
2
4
Z 2 me e 4
E1
2 2
Оператор спин орбитального взаимодействия VˆS ,L
ˆ ˆ
2
a (L S )
Z E1 1
2
r
3

15. Приближение LS связи

Состояние всего набора электронов в атоме
приближенно зависит от квантовых чисел
• полного орбитального момента L
• полного спинового момента атома S
L L li
i
qL 2 L 1, штук проекций ( кратность вырождения по L)
Lz / L, L 1,...,0,...L 1, L
S si , S z / S , S 1,..., S 1, S
i
qS 2 S 1 штук проекций ( кратность вырождения по S )
В силу сферической симметрии

16. Приближение LS связи

Интегралы движения – J = L + S
• Квадрат полного орбитального момента L2
• Квадрат полного спинового момента S2
J L S
M J J , J 1,...,0,1,..., J 1, J , всего 2 J 1
2
L 2 L( L 1),
Lz / L, L 1,...,0,...L 1, L
2
S 2 S ( S 1),
всего 2 S 1 штук
Полная кратность вырождения без
LS взаимодействия ( 2 L 1) ( 2 S 1)
учета

17. Приближение LS связи

Полный орбитальный момент L
не является интегралом движения –
не сохраняется –
т.к. не коммутирует с Гамильтонианом
Полный спиновый момент атома S также
не является интегралом движения –
не сохраняется –
т.к. не коммутирует с Гамильтонианом.
При учете спин орбитальной связи L и S по
отдельности не являются интегралами
движения .
Уровни энергии в атоме становятся зависимыми
от полного момента импульса J = L + S
Интегралы движения J, L2 , S2 .

18. Приближение LS связи

J L S,
Приближение LS связи
J 2 J ( J 1),
2
JZ MJ
L S J L S,
L S,
всего
2S 1
S L J L S,
L S,
всего
2L 1
При фиксированном
J
проекция J M J J ,
всего 2 J 1
Полное число компонент на которое
расщепляется уровень энергии с заданными L, S -
g L ,S
L S
2 J 1 2S 1 2 L 1
L S
Поправка к уровню энергии при заданных L, S -
EL ,S VˆL ,S

19. Расчет поправки ls связи.

20. Поправка LS связи

Оператор LS взаимодействия в обкладках ВФ с
квантовыми числами J, MJ
VˆS ,L
ˆ ˆ
1
e2
2 2 3 L S ( Z )
2 me c r
Первая поправка по теории возмущений
в базисе собственны х
WSL nlJM
VˆS ,L nlJM
J
J
ВФ полного
1 e2
2 2 nlJM
2 me c
J
Необходимо:
1.определить собственные числа
оператора (L S)
2. выполнить осреднение 1/r3
момента J
1 ˆ ˆ
L S nlJM
3
r
J

21. Поправка LS связи

Собственные числа оператора (L S)
J L S
2 2 2
J L S 2 L S
ˆ 2 ˆ2 ˆ 2
ˆ ˆ
1
L S J L S
2
ˆ 2
ˆ2
ˆ 2
ˆ ˆ
1
J
L S
S
L
nlJM
nlJM
nlJM
nlJM
2
2
J ( J 1) L( L 1) S ( S 1) nlJM
2
J
J
J
J
J

22. Поправка LS связи

Осреднение 1/r3 в обкладках радиальных ВФ
1
1
2
1
Rn ,l 3 Rn ,l r dr Rn ,l Rn ,l dr
3
r
r
r
0
0
2( Z ) ( n l 1)!
Zr 2 Zr 2 l 1 2 Zr
Rn ,l
exp
Ln l
2
3
n
[( n l )! ]
n n
n
l
3/ 2
Z 1
2
1
2 ( n l 1)! 1
2 r / na 2 r 2 l 1 2 r
2
dr e
Ln l
3
3
r
n [( n l )! ] 0 r
na
n
1
3 3
l l 1 / 2 l 1 n a
2l

23. Поправка LS связи

Пример. Осреднение 1/r3 для 2p состояния (n=2, l=1)
1
1
2
1
Rn ,l 3 Rn ,l r dr Rn ,l Rn ,l dr
3
r
r
r
0
0
1
5/ 2
R2 ,1
Z r exp( Zr / 2), Z 1
24
1
1 d 2 r 1
r
e
d
e
3
r
24 0
24 0
1
1
e | e d
0
24
0
24
1
1
3
r
24 a 3

24. Поправка LS связи

Окончательно: поправка WLS
WL ,S
e
J ( J 1) L( L 1) S ( S 1)
2 2
3 3
2me c 2 L ( L 1 / 2) ( L 1) n a
2
2
Ry J ( J 1) L( L 1) S ( S 1)
3
3 3
n
L ( L 1 / 2) ( L 1) n a1
2
4
me
Ry 2 ,
2
2
e
,
c
a1 2
me
2

25. Поправка LS связи

Расщепление уровня с заданными L, S - WLS
ˆ ˆ
1
WL ,S A L S A J ( J 1) L( L 1) S ( S 1 ,
2
E между J , J 1
A
E J ( J 1) ( J 1) J A J
2
E = A/2 J – правило интервалов Ланде.
Энергия уровня зависит от L, S сильно,
от J (при заданных L, S) слабо.
Слабая зависимость от J выражается в тонкой
структуре атомарных спектров.

26. Оболочечная модель.

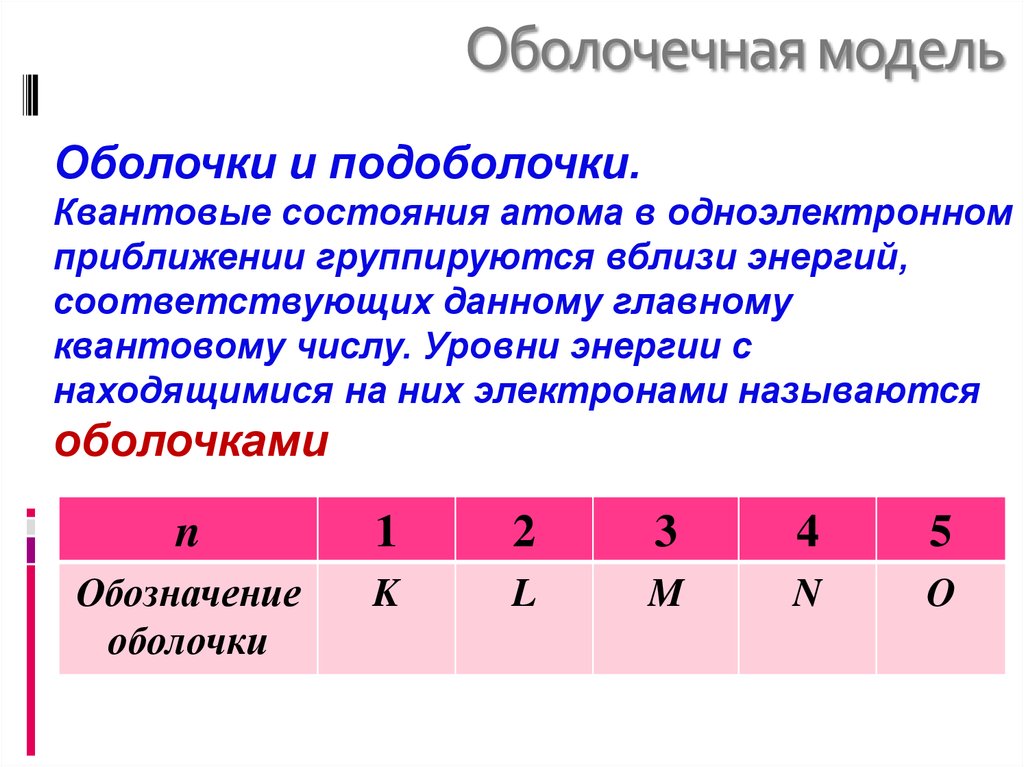
27. Оболочечная модель

Оболочки и подоболочки.
Квантовые состояния атома в одноэлектронном
приближении группируются вблизи энергий,
соответствующих данному главному
квантовому числу. Уровни энергии с
находящимися на них электронами называются
оболочками
n
1
2
3
4
5
Обозначение
оболочки
K
L
M
N
O

28. Оболочечная модель

Подоболочка.
Внутри оболочки располагаются уровни энергии,
зависящие от орбитального квантового числа l
В свободном атоме число состояний с
квантовым числом l равно числу возможных
проекций, всего 2(2l+1) штук (2-число проекций s)
Уровни энергии с заданным значением l в
пределах определенной оболочки образуют
подоболочку
l
0
1
2
3
4
Обозначение
подоболочки
s
p
d
f
g

29. Оболочечная модель

Максимальное число электронов.
Максимальное число электронов в подоболочке 2(2l+1)
Квантовое число l меняется в диапазоне от l = 0
до l = n – 1
Максимальное число электронов в
оболочке
n 1
2 2l 1 2n
2
l 0
Множитель 2 – число проекций спина

30. Оболочечная модель

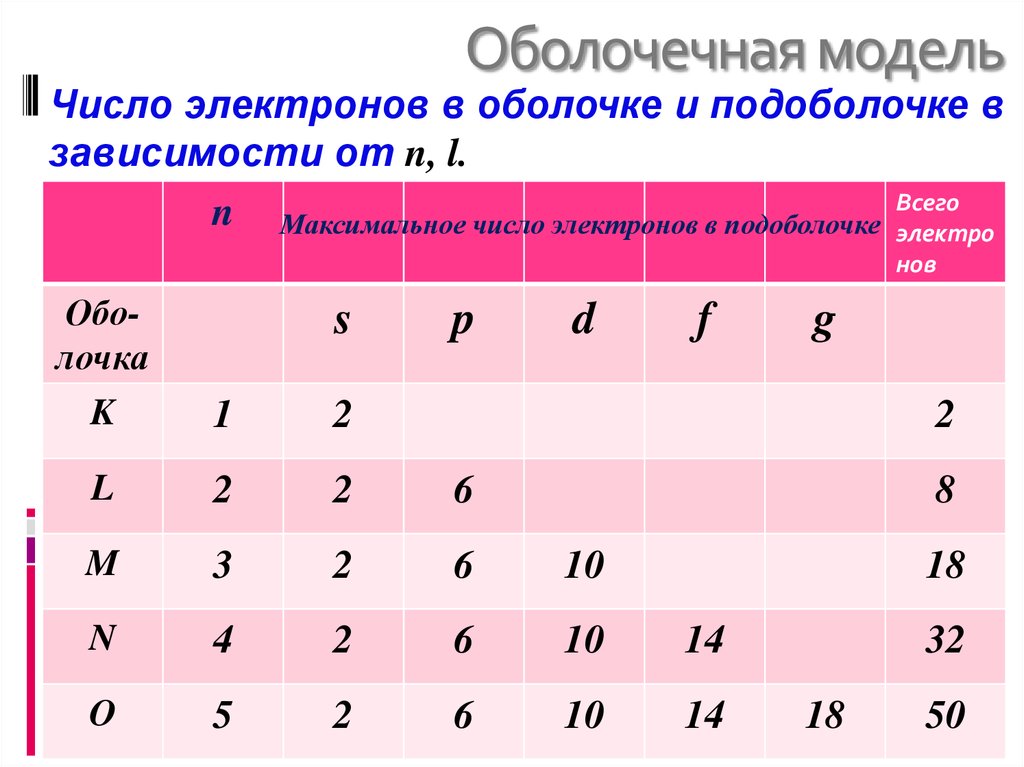
Число электронов в оболочке и подоболочке в
зависимости от n, l.
n Максимальное число электронов в подоболочке Всего
электро
нов
Оболочка
K
1
2
L
2
2
6
M
3
2
6
10
N
4
2
6
10
14
O
5
2
6
10
14
s
p
d
f
g
2
8
18
32
18
50

31. Оболочечная модель

Df. Полностью заполненные оболочки
называются замкнутыми.
Электроны замкнутых оболочек слабо
взаимодействуют с электронами других атомов.
Атомы с замкнутыми оболочками химически
инертны.
Df. Электроны незаполненных оболочек
называются валентными.
Взаимодействие валентных электронов с
электронами других атомов приводит к образованию
устойчивых химических соединений.

32. Электронные конфигурации.

33. Электронные конфигурации

Df.Состояния отдельных электронов в
атоме обозначаются символами n l y . n –
главное квантовое число, l орбитальное
квантовое число. y - число электронов в
атоме с данными n, l
Примеры. 1.Электронная конфигурация основного
состояния атома Na: 1s2 2s2 2p6 3s
2. Основное состояние атома N: 1s2 2s2 2p3
Df. Все электроны определенной подоболочки
называются эквивалентными.
Пример. ns2,
nd5,
nf12

34. Терм. Мультиплетность терма.

35. Терм

Уровни из набора (2L+1)(2S+1) штук, принадлежащие определенной электронной конфигурации с заданными L, S называется
термами.
Обозначения термов
2 S 1
LJ
Символьные обозначения термов
L 0, 1, 2, 3, 4, 5, 6,...
S
P D F
G
H
I ...
Число 2S+1 называется мультиплетностью
терма

36. Терм

Число уровней:
При L S M J 2 S 1
При L S M J 2 L 1
2 L 1 2 S 1 меньше
Синглетный терм
Дублет
Триплет
мультиплетности
S=0
S=1
S=2

37. Терм

Заполненная (замкнутая) оболочка имеет
L = 0 и S = 0. Тогда проекции Lz и Sz
симметрично имеют все положительные и
отрицательные значения.
Основное состояние атома с заполненными
оболочками соответствует терму 1S0
Вклад в L и S атома происходит от
электронов на незаполненных оболочках

38. Терм

Наиболее просто определяются термы электронов на
незаполненных оболочках с различными n, l – в этом
случае нет ограничений по принципу Паули.
Пример. Термы 2-х н.э. электронов 1) np + 2) nf электронов.
1) ml m 1, 0, 1; 2) ml m 3, 2, 1, 0, 1, 2, 3
1) ms 1 / 2, 1 / 2;
2) ms 1 / 2, 1 / 2
S s1 s2 ,..., s1 s2 0, 1;
L l2 l1 ,... l2 l1 3 1... 3 1 2, 3, 4
J L S ,..., L S 2 1 ,..., 4 1 1, 2,...., 4, 5
G ( L 4) J 4 ,
2 S 1 1
G ( L 4 ) J 5 , 4 , 3 ,
2 S 1 3
F ( L 3) J 3 ,
2 S 1 1
F ( L 3) J 4 , 3, 2 ,
2 S 1 3
D ( L 2) J 3 ,
2 S 1 1
D ( L 2) J 3, 2 ,1
2 S 1 3

39. Правила хунда.

40. Правила Хунда

Терм при данной конфигурации,
соответствующий наименьшей энергии.
Df. 1. Из всех термов данной конфигурации
наименьшей энергией Emin обладает терм с
наибольшим значением полного спина Smax.
При данном S наименьшую энергию имеет терм с
наибольшим значением квантового числа
орбитального момента L
Df. 2. Полный момент J терма с наименьшей
энергией равен: а) J = |L - S|, если оболочка
заполнена менее чем наполовину;
б) J = |L + S|, если оболочка заполнена более чем
наполовину

41. Правила Хунда

2
Правила Хунда
Примеры. 1. Конфигурация 2 p - 2 эквивалентных
электрона из 6 возможных. Заполнение менее чем
3
наполовину. Терм с минимальной энергией P0
2. 3 эквивалентных электрона
ml
ms
ms
ms
+1
0
-1
Ms
ML
p3
ms
p
3
li =1
ms
ms
ms
3/2
1/2
1/2
1/2
1/2
1/2
1/2
0
0
0
0
2
1
1

42. Правила Хунда

2. 3 эквивалентных электрона
Правила Хунда
p
3
M L 2, M S 1 / 2
M L 1, M S 1 / 2 L 2, S 1 / 2
M L 0, M S 1 / 2
M L 1, M S 1 / 2
L 1, S 1 / 2
M L 0, M S 1 / 2
M L 0, M S 3 / 2
L 0, S 3 / 2
M L 0, M S 1 / 2
3 терма:
4
2
2
S , P , D

43. Правила Хунда

Результаты справедливы при слабой L, S связи.
Расстояние между подуровнями тонкой
структуры в спектре малы по сравнению с
разницей между уровнями энергий при различных L
и S. Векторы полного орбитального момента и
полного спинового момента приближенно
сохраняются. Спин орбитальная связь приводит к
слабому расщеплению уровней.
Противоположный предельный случай – спин
орбитальное взаимодействие велико по сравнению
с взаимодействием электронов между собой.
Приближенно складываются моменты отдельных
образуя полный момент электрона j=l+s. В
следующем приближении моменты электронов
суммируются в полный момент атома. J= j
Связь типа J-J связь.

44. Интернет ресурс

http//:edu.ci.nsu.ru
Курс лекций
Задачник