Похожие презентации:
Несобственные интегралы. Функции нескольких переменных: область определения, линии уровня, частные производные
1.
Лекция N1Лектор: проф. ОРЛИК ЛЮБОВЬ
КОНСТАНТИНОВНА
Тема: Несобственные интегралы.
Функции нескольких переменных: область
определения, линии уровня, частные
производные
2.
1. Несобственные интегралы.b
В определении
f ( x ) dx
a
предполагается, что a, b - конечные
числа, а f ( x) - непрерывная функция.
Если хотя бы одно из этих условий
нарушается, то интеграл называется
несобственным.
3.
Мы рассмотрим интегралы побесконечному промежутку или
несобственные интегралы 1-ого рода:
a
B
f ( x) dx lim
B
f ( x) dx.
a
Если такой предел существует и
конечен, то говорят, что несобственный
интеграл сходится.
4.
Если же указанный предел несуществует или бесконечен, то говорят,
что интеграл расходится.
Аналогично определяется
b
где
b
f ( x) dx lim
f ( x) dx
A
c
f ( x) dx.
A
f ( x) dx
f ( x) dx,
c
c - любая фиксированная точка оси Ox.
5.
Пример.1 B
B
dx
x
2
lim
x
dx
lim
2
1 x B 1
B 1
1
1
lim 1 1,
B
B
следовательно
dx
1 x 2
сходится.
6.
На практике при вычислениинесобственных интегралов можно сразу
применять формулу Ньютона-Лейбница и
символ « » подставлять как число.
Пример.
dx
arctg
x
0 1 x 2
0
arctg( ) arctg(0)
2
0
2
.
7.
Теорема.1,
dx
:
1 x 1,
сходится,
расходится.
8.
Функция двух переменныхПример. Площадь z прямоугольника со
сторонами x, y находится по формуле
z xy.
Эта формула определяет функцию двух
переменных x и y .
Областью определения функции
z z ( x, y) является некоторое
множество точек плоскости Oxy.
9.
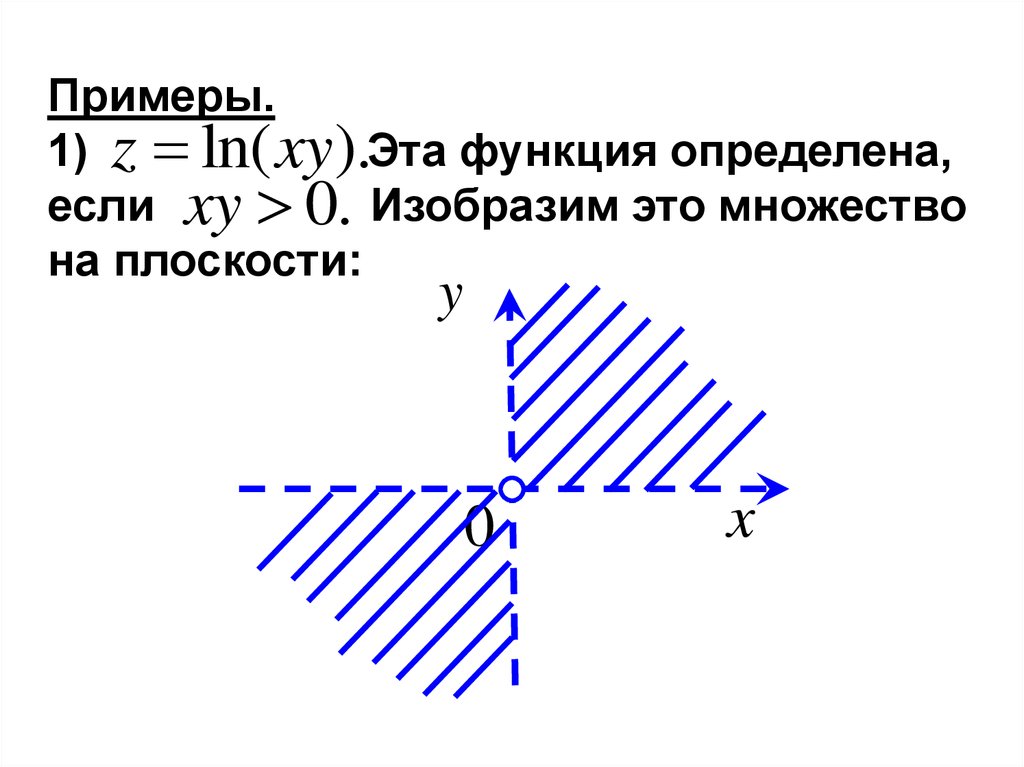
Примеры.1) z ln( xy ).Эта функция определена,
если xy 0. Изобразим это множество
на плоскости:
y
0
x
10.
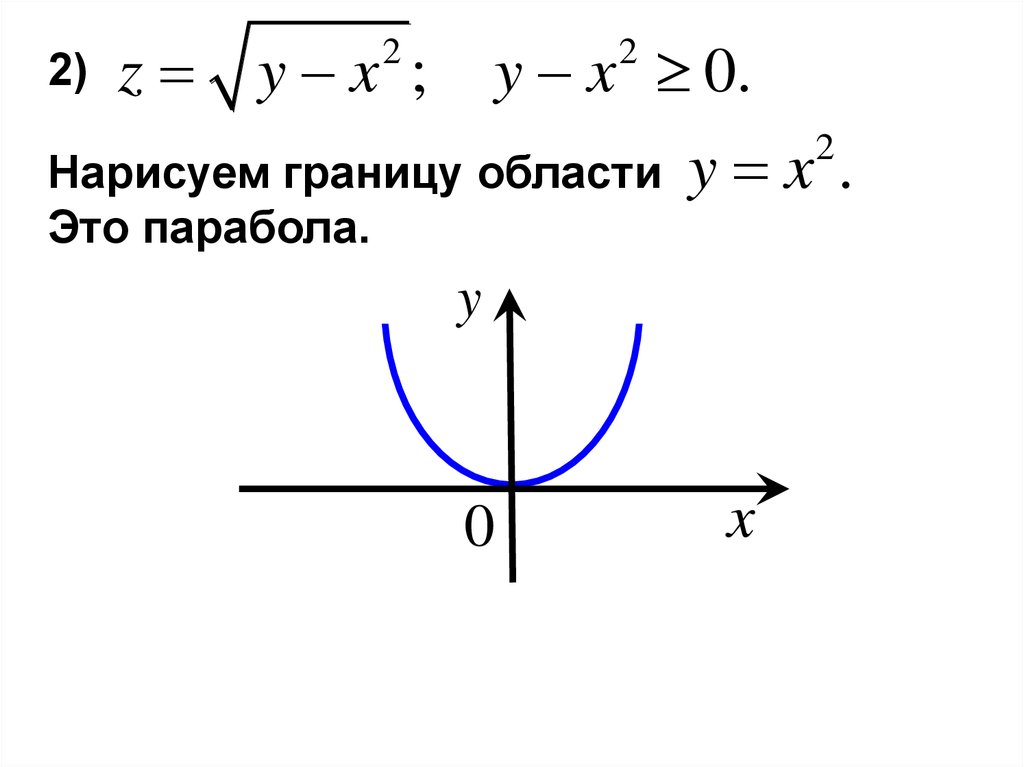
2)z y x ;
y x 0.
2
2
Нарисуем границу области
Это парабола.
y x .
2
y
0
x
11.
Парабола делит область на две части.Достаточно взять одну точку, например
M (0;1),и проверить выполнение
неравенства
2
y x 0 1 0 0 (верно)
y
D
M
0
x
Следовательно, областью определения
является множество точек D.
12.
График функции двух переменныхГрафиком функции двух переменных
является поверхность.
Примеры.
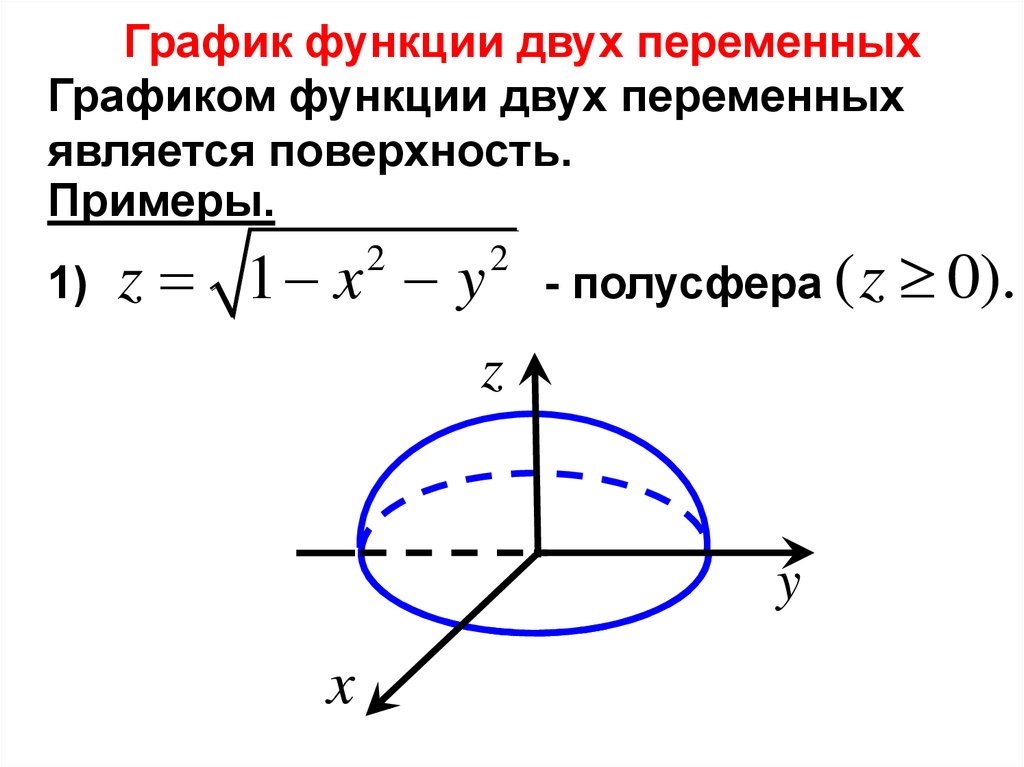
1)
z 1 x y
2
2
- полусфера ( z
z
y
x
0).
13.
2)z x y
2
2
- параболоид.
z
y
x
14.
Построение графиков функций двухпеременных представляет
значительные трудности. Поэтому
существует еще один способ
изображения функции двух
переменных, основанный на сечении
поверхности z f ( x, y ) плоскостями
z c, где c - любое число, т.е.
плоскостями, параллельными
плоскости Oxy.
15.
Назовем линией уровня множествоточек плоскости z ( x, y ) c, где c число. Термин «линии уровня» взят из
картографии. Там линии уровня – это
линии, на которых высота точек земной
поверхности над уровнем моря
постоянна. По ним можно судить и о
характере рельефа, что особенно
важно, если местность гористая.
16.
Пример. Построить линии уровняфункции z x 2 y 2 .
Линии уровня определяются уравнением
x y c (0 c ).
Давая c различные значения, получаем
2
2
семейство концентрических окружностей.
17.
c 0:(0,0).
(радиус r 1
(радиус r 2
получается точка
c 1: x y 1
2
2
2
c 4: x y 2
c 0
y 2
2
2
c 1
1
x
c 4
)
)
18.
Частные производныеРассмотрим функцию z z ( x, y ).
Зафиксируем одну переменную,
например, y.Пусть y y0 . Тогда
получится функция одной переменной x.
Производная от такой функции
называется частной производной по x
z
.
и обозначается z x или
x
z
Аналогично определяется z y или
y
y
(
- переменная, x - постоянная).
19.
Пример.1) Найти
z x
и
z y ,
если
z x y 2 xy.
3
2
z x y ( x ) x 2 y x 3x y 2 y.
2
3
2
2
z y x ( y ) y 2 x y 2 yx 2 x.
3
2
3
20.
Частные производные 2-ого порядкаФункция z z ( x, y ) имеет четыре
частные производные второго порядка.
z xy
( z x ) x z xx
( z y ) x z yx
( z x ) y z xy
( z y ) y z yy
и z yx называются
смешанными производными.
21.
Теорема.Смешанные производные z xy и z yx
равны между собой при условии их
непрерывности:
z xy z yx .
22.
Пример.1) Найти частные производные второго
порядка функции
z x y .
3
z x 3x y ,
2
2
2
z xx (3x y ) x 3 y 2 x 6 xy .
2
2
2
z y 2 x y,
3
3
z yy (2 x y) y 2 x .
3
2
23.
z xy ( z x ) y (3x y ) y 2 y 3x 6 x y,2
2
2
2
z yx ( z y ) x (2 x y) x 2 3x y 6 x y.
Мы видим, что z xy z yx .
3
2
2
24.
Полный дифференциал функцииПусть z z ( x, y ). Полный
дифференциал
dz z x dx z y dy.
z x y. Найти dz.
2
z x 2 xy, z y x
2
dz 2 xy dx x dy.
Пример.
2
25.
Дифференцирование сложных функцийПусть z z ( x, y ), причем
x x(t ), y y(t ).
Тогда z есть сложная функция одной
переменной t :
dz z dx z dy
.
dt x dt y dt
26.
Рассмотрим теперь функцию f ( x, y )при условии, что y y ( x). Здесь
переменная z есть функция одной
переменной x : z f x, y ( x) .
Этот случай сводится к предыдущему,
причем роль переменной t играет x.
dz z dx z dy
.
dx x dx y dx
27.
Ноz
x
dx
1
dx
dz z z dy
.
dx x y dx
- частная производная, которая
находится так, как если бы
зависел от x .
y
не
28.
dzdx
- производная сложной
функции одной переменной. Эту
производную называют полной
производной.
29.
Примеры.z x y, где y cos 2 x.
z
dz
Найти
и
.
x
dx
z
1)
2 xy.
x
Затем вместо y подставим y cos 2 x.
Получим
z
2 x cos 2 x.
x
2
30.
dzz
z
dy
2)
;
dx x y dx
z
dy
2
x ;
2sin 2 x
y
dx
dz
2
2 x cos 2 x 2 x sin 2 x.
dx
z
Ответ:
2 x cos 2 x,
x
dz
2
2 x cos 2 x 2 x sin 2 x.
dx
31.
Самостоятельная работа №21) Найти область определения функций
a) z xy ,
b) z
1
.
x y 1
2) Найти частные производные первого
и второго порядка
b) z x 3xy.
a) z x y ,
3
3) z x ln y, где y 5sin x.
dz
z
.
Найти
и
dx
x
3
4
2



















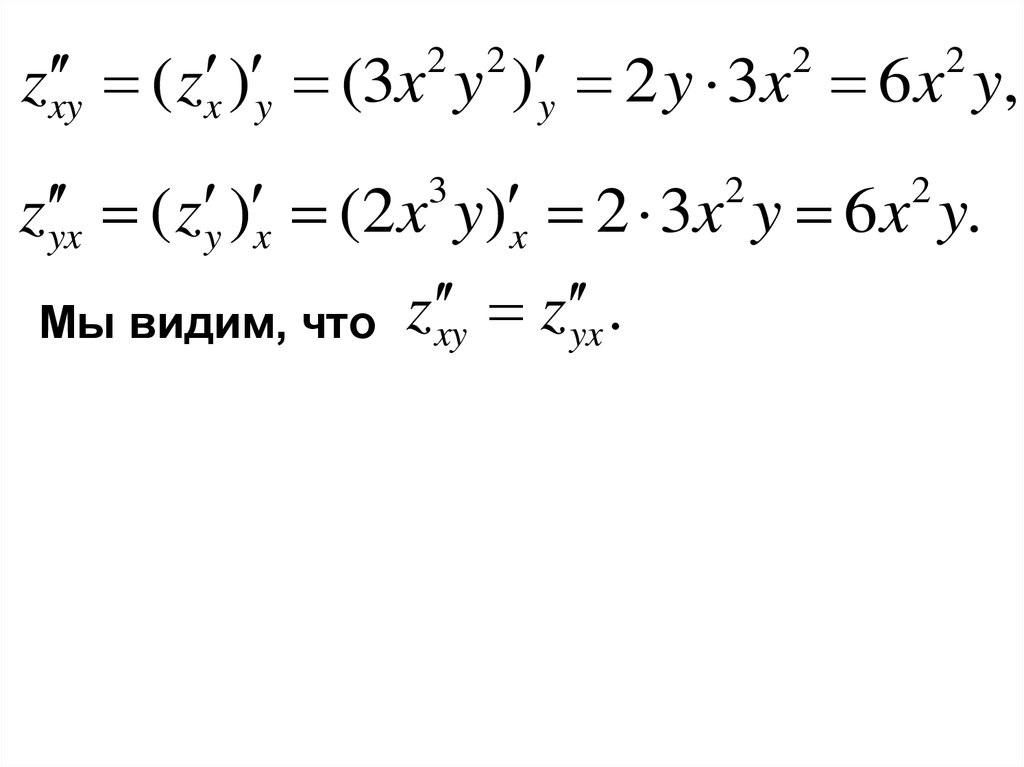








 Математика
Математика








