Математические модели движения ракет класса «поверхность-поверхность» в плотных слоях атмосферы

1.

МАТЕМАТИЧЕСКИЕ МОДЕЛИ ДВИЖЕНИЯ РАКЕТ
КЛАССА «ПОВЕРХНОСТЬ-ПОВЕРХНОСТЬ»
В ПЛОТНЫХ СЛОЯХ АТМОСФЕРЫ
Этапы разработки и реализации математической модели
Выбор основных допущений математической модели
Определение системы сил, действующих на ракету
Выбор необходимых систем координат
Разработка математической модели - получение дифференциальных уравнений,
описывающих движение ракеты и дополнительных соотношений
Разработка численной модели процесса
Реализация численной модели на ЭВМ. Программирование, отладка программы
Тестирование программы по результатам контрольных расчетов

2.

Основные допущения
1. Наличие
ракеты.
осевой
аэродинамической
симметрии
2. Совпадение вектора силы тяги с продольной осью
ракеты (отсутствие аэродинамического эксцентриситета).
3. Малость углов атаки-скольжения, допущение о
возможности
линеаризации
уравнений
движения
cos 1 sin
(___________________).
4. Неучет кривизны и вращения Земли.
5. Отсутствие ветра.

3.

Векторное уравнение движения центра
масс ЛА
d *V
m
V F F p
dt
скалярные уравнения
в некоторой i-ой подвижной системе
координат с началом в центре масс ЛА
в проекциях на оси
траекторной системы координат
Fxi Fpxi
V xi yiVzi ziV yi
m
m
Fxk Fpxk
V
m
m
Fyi Fpyi
V yi ziVxi xiVzi
m
m
Fy
Fpy
V
Fzi Fzxi
V zi xiV yi yiVxi
m
m
Fz
Fpx
V
k
zk
m
m
k
yk
m
k
k
m

4.

Определение проекций угловой скорости вращения траекторной системы координат
Yк
Y0
yк
xк
zк
Z0
Xк
X0
Zк
sin
xк
Fxk Fpxk
V
m
m
cos
yк
Fzk Fpxk
V cos
m
m
zк
V
Fy Fpy
k
m
m
k

5.

Уравнения вращательного движения записывают в проекциях на оси
связанной системы координат
Векторное уравнение изменения кинетического момента
*
dK d K
K MR
dt
dt
соответствующее ему матричное уравнение
I XX 0 0 x x I XX 0 0 x M x M px
0 I YY 0 y y 0 I YY 0 y M y M py
0 0 I 0 0 I
ZZ z
ZZ z
z
M z M pz
x
y
z
M x M px
I XX
M y M py
I YY
M z M pz
I ZZ
I ZZ I YY
y z
I XX
I XX I ZZ
x z
I YY
I I XX
YY
y x
I ZZ

6.

К определению проекций угловой скорости ракеты
x sin
y cos cos sin
z cos sin cos
y sin z cos
1
( y cos z sin )
cos
x tg ( y cos z sin )

7.

XYZ
X кYк Z к
X кYк Z к
X g Yg Z g
cos cos - sin cos sin
- sin cos
sin
cos cos
cos
0
cos a sin sin a cos sin cos a cos sin a sin sin - sin a cos sin
sin sin cos cos sin sin cos cos sin sin cos cos
cos sin sin cos cos
a
a
a
a
a
cos cos - cos sin cos sin sin cos sin sin sin cos
cos cos
- cos sin
sin
sin cos cos sin sin sin cos cos cos sin sin sin
,
XYZ
X g Yg Z g
Соотношения между углами:
sin sin cos cos cos (sin cos a cos sin sin a )
sin cos sin cos cos a cos (sin cos sin a sin cos )
cos sin sin ;
cos sin sin a cos cos sin sin

8.

Текущие значения координат
x g V cos cos
y g V sin
z g V cos sin
Уравнение для текущей массы ракеты
t
m m0 m dt
0
Наклонная дальность – расстояние до центра масс ракеты
r x2 y2 z 2
Характеристики движения ракеты
V (t ); (t ); (t ); xg (t ); y g (t ); z g (t ); (t ); (t ); (t ); (t ); (t ); a (t );
x (t ); y (t ); z (t ); mx (t ).

9.

Система уравнений движения ЛА в плотных слоях атмосферы
1. V
1
[( Px X p X a ) cos cos ( Py Y p Ya ) sin cos
m
( Pz Z p Z a ) sin mg sin ];
1
2.
[( Px X p X a ) sin cos a ( Py Y p Ya ) cos a cos
mV
( Pz Z p Z a ) sin a cos mg cos ];
1
[ ( Px X p X a ) cos a cos sin
mV cos
( Py Yp Ya ) sin a cos ( Pz Z p Z a ) cos a cos ];
3.
1
( M x M px );
I xx
1
5. y
( M y M py );
I yy
4. x
1
6. z
( M z M pz );
I zz
7. y sin z cos ;
1
8.
( y cos z sin );
cos
9. x tg ( y cos z sin );
10. sin sin cos cos cos sin cos a ;
11. sin cos sin cos cos a cos (sin cos sin a sin cos )
cos sin sin ;
12. cos sin sin a cos cos sin sin ;
13. x g V cos cos ;
14. y g V sin ;
15. z g V cos sin ;
t
16. m m0 m dt.
0
17. r x 2 y 2 z 2
Упрощения
1. x 0; 0; 0
2. M x M px 0;
M y M py 0;
M z M pz 0
б ; б ; б
3. , , , a малы
sin( , , , a ) , , , a
cos( , , , a ) 1
(*)

10.

Уравнения продольного (плоского) движения ракеты
1
V [( Px X p X a ) cos ( Py Yp Ya ) sin mg sin ];
m
x g V cos ;
y g V sin ;
1
[( Px X p X a ) sin ( Py Yp Ya ) cos mg cos ];
mV
1
z ( M z M pz );
I zz
;
z
t
m m0 m dt.
;
0
Уравнения бокового движения ракеты и вращения по крену
x
.
y
1
[ ( Px X p X a ) cos a sin
mV cos
( Py Yp Ya ) sin a ( Pz Z p Z a ) cos a cos ];
x tg ( y cos z sin );
1
( M x M px );
I xx
M y M py
I yy
sin a
I xx I zz
x z ;
I yy
1
( y cos z sin );
cos
cos sin sin sin
;
cos cos
z g V cos sin ;
sin
sin cos sin cos a sin a sin sin sin
cos

11.

Система дифференциальных уравнений для оценки дальности стрельбы
неуправляемых ракет
P Xa
V x
g sin ;
m
g cos
.
;
V
x g V cos ;
y g V sin ;
m m0 m dt.
для пассивного участка траектории
P Xa
V x
g sin ;
m
g cos
;
V
t
y g V sin ;
x g V cos
0

12.

Тема № 7. УСТОЙЧИВОСТЬ ДВИЖЕНИЯ
И СТАБИЛИЗАЦИЯ СНАРЯДОВ
Содержание
1. Устойчивость полета снарядов, стабилизированных вращением
2. Устойчивое движение на траектории оперенного снаряда
3. Явление резонанса проворачивающихся оперенных снарядов
4. Явление резонанса удлиненных нежестких ЛА

13.

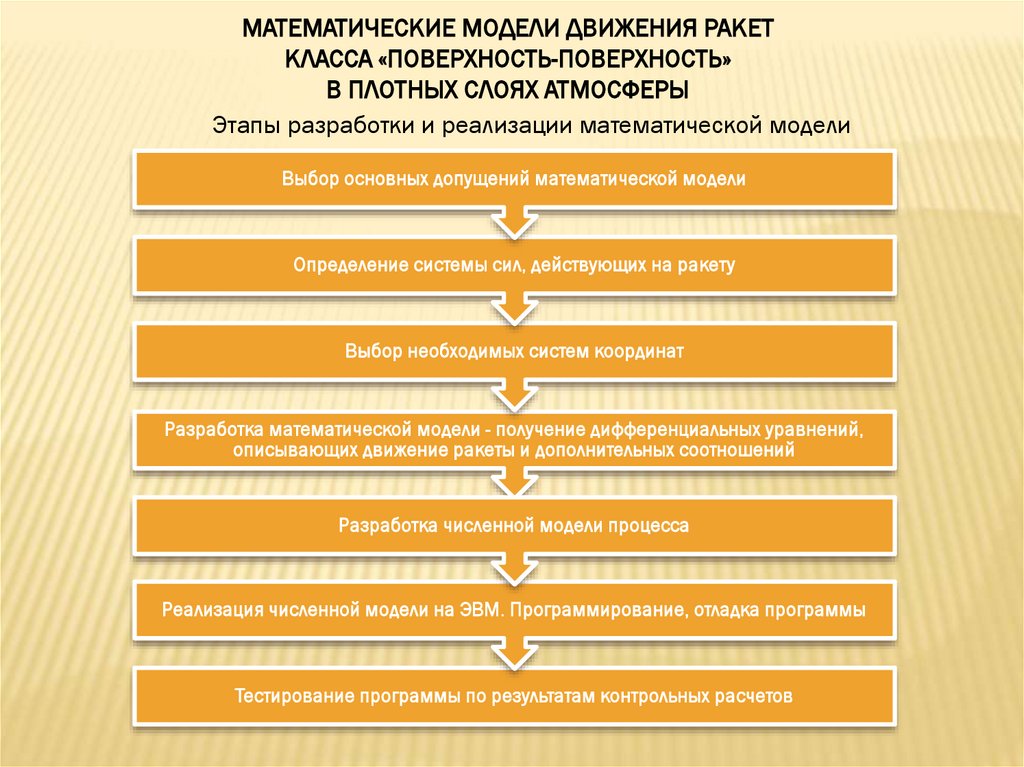
Схема последовательных положений оперенного снаряда
на траектории при правильном полете
Схема действия аэродинамического момента:
а — на неоперенный снаряд (ракету); б — на оперенный снаряд

14.

Устойчивость полета ракет и снарядов,
стабилизированных вращением
Угловая скорость
Угловая скорость прецессии
При 0
0
sin t
2
T
0
A
x
2 Vд 2 V0
d
d
I r
zz 0
I xx
r0 x cos x
При
0
0
sh t
Условие гироскопической устойчивости снаряда –
положительное значение коэффициента
гироскопической устойчивости
0

15.

Физический смысл
1
2
0
V 2
Mz
Sm mz
2
M z I zz
V 2
Smmz
2 I zz
V 2 Sm mz
1
0
2
2 I zz
2 2
V 2 Sm mz
2 I xx x
2
2
I zz
4 I zz
Необходимая угловая скорость вращения ЛА относительно продольной оси
V
x
2 I zz Smmz
kI xx

16.

Устойчивое движение на траектории оперенного снаряда
Условие устойчивости оперенного снаряда выполнение неравенства
xцд xцм 0
Коэффициент запаса устойчивости
C
mz y
mz
C
y
xцд xцм
l
100 %
mi xCi
xцм
mi
xцд
xцдк С
yк xцдопС yоп
С
yк С yоп

17.

Явление резонанса проворачивающихся оперенных снарядов
Значение критической угловой скорости
аксиального вращения
кр V
Sml mz
2( I zz I xx )
Условие возникновения резонанса
совпадение частот аксиального и экваториального вращений снаряда
Явление резонанса удлиненных нежестких ЛА
2
2 y
2 y
EJ ( x)
m( x )
q ( x, t )
2
2
2
x
x
t
y ( x, t ) f n ( x)qn (t )
n 1
EJ0
Частота собственных колебаний
n 2n
cos n ch n 1 0
2 7,85 3 11,0
1 4,73
m0l 4
Условие возникновения резонанса совпадение частоты вращения ракеты относительно продольной оси с
частотами упругих изгибных колебаний корпуса ракеты