Похожие презентации:
Применение определителей 2 и 3 порядка в решении задач координатно – векторным методом (ЕГЭ)
1.
ПРИМЕНЕНИЕ ОПРЕДЕЛИТЕЛЕЙ 2 И 3 ПОРЯДКА В РЕШЕНИИ ЗАДАЧ№14 ЕГЭ ПО МАТЕМАТИКЕ КООРДИНАТНО – ВЕКТОРНЫМ МЕТОДОМ.
Выполнил: Каримов Н.Х.
учитель
МБОУ «Кутлушкинская средняя
общеобразовательная школа».
2.
СОДЕРЖАНИЕ:1. Введение.
2. Нахождение угла между плоскостями.
3. Нахождение угла между прямой и плоскостью.
4. Нахождение расстояния от точки до плоскости.
5. Заключение.
3.
1. Введение.Цель данной работы рассмотреть координатно – векторный метод решения
задач №14 из ЕГЭ по математике и показать возможность применения
определителей третьего порядка для нахождении уравнения плоскости.
Метод координат — весьма эффективный и универсальный способ нахождения
любых углов или расстояний между стереометрическими объектами в пространстве.
Данный метод решения заключается во введении (привязке к исследуемым
фигурам) декартовой системы координат, а затем – исчислении образующихся
векторов (их длин и углов между ними).
Преимущество координатного метода перед альтернативным решением
средствами дополнительных построений состоит в том, что удается
полностью отстраниться от чертежа и заниматься исключительно числами
(координатами).
4.
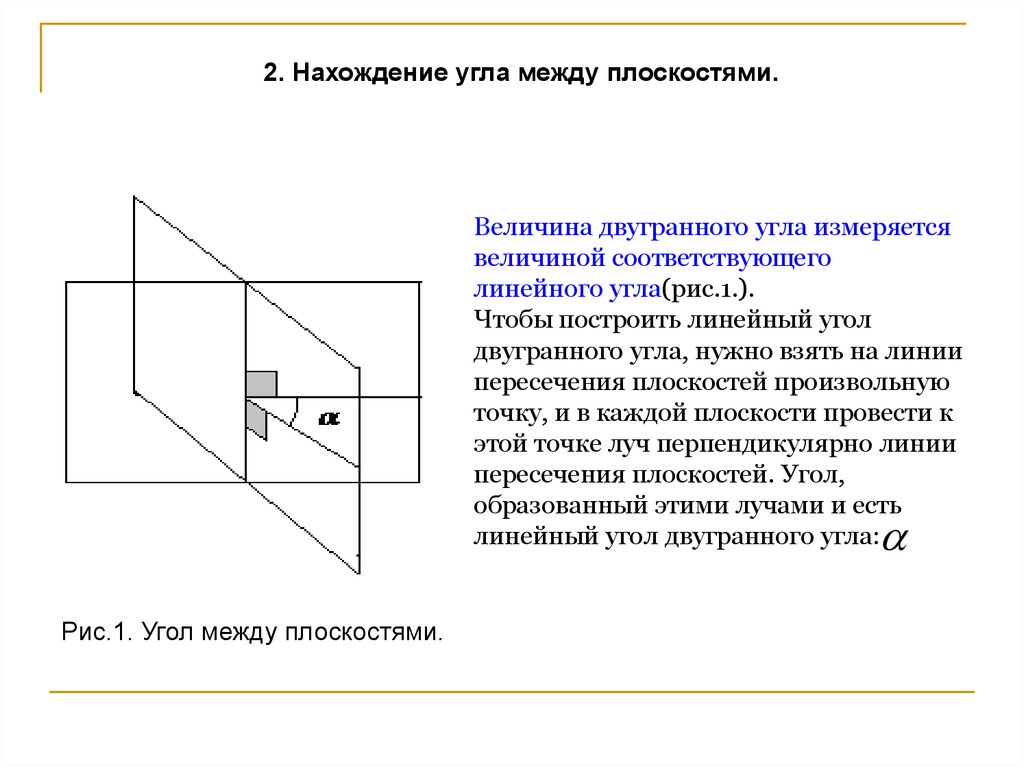
2. Нахождение угла между плоскостями.Величина двугранного угла измеряется
величиной соответствующего
линейного угла(рис.1.).
Чтобы построить линейный угол
двугранного угла, нужно взять на линии
пересечения плоскостей произвольную
точку, и в каждой плоскости провести к
этой точке луч перпендикулярно линии
пересечения плоскостей. Угол,
образованный этими лучами и есть
линейный угол двугранного угла:
Рис.1. Угол между плоскостями.
5.
В высшей математике есть такое правило, которое позволит нам с легкостьюрешать задания данного типа методом координат.
Угол между двумя плоскостями в пространстве равен модулю угла между
нормалями к этим плоскостям.
Таким образом, если мы найдем координаты вектора нормали, то
воспользовавшись формулой косинуса угла между векторами, известной из
школьного курса геометрии, найдем искомый угол.
n1 n2
cos
n1 n2
6.
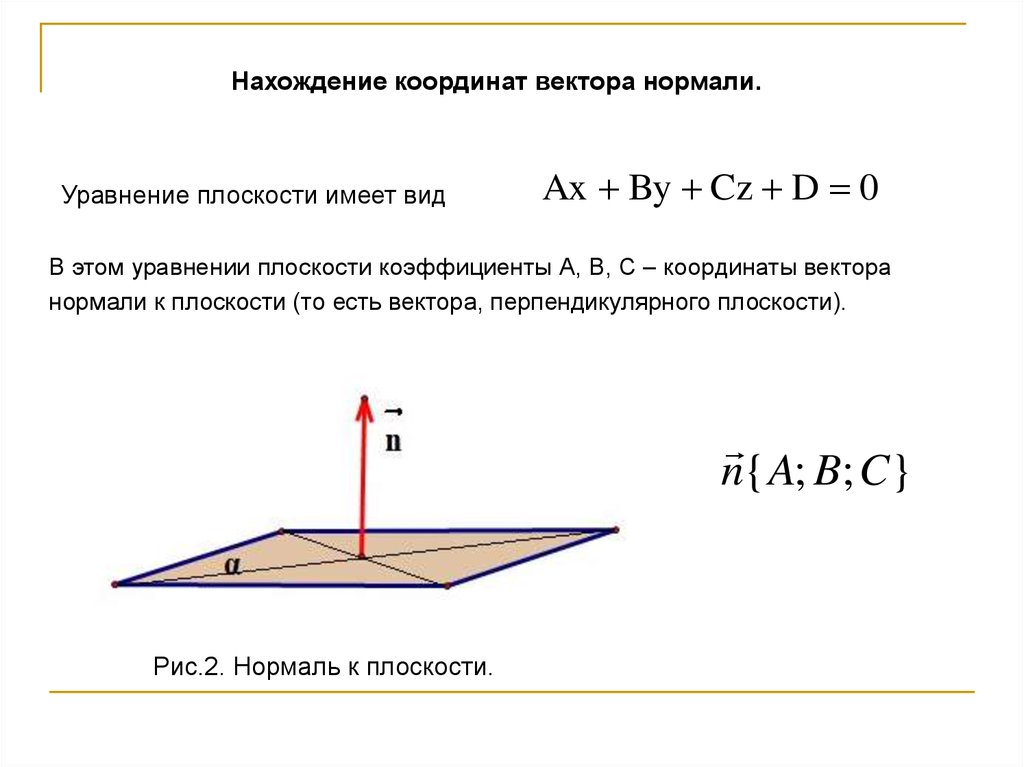
Нахождение координат вектора нормали.Уравнение плоскости имеет вид
Ax By Cz D 0
В этом уравнении плоскости коэффициенты А, В, С – координаты вектора
нормали к плоскости (то есть вектора, перпендикулярного плоскости).
n{ A; B; C}
Рис.2. Нормаль к плоскости.
7.
Нахождение уравнения плоскости через определитель.Уравнение плоскости проходящей через точки M1 ( x1 ; y1 ; z1 ) M2 ( x2 ; y2 ; z2 )
M 3 ( x3 ; y3 ; z3 ) в координатной форме будет иметь вид:
x x1
y y1
z z1
x2 x1
y 2 y1
z 2 z1 0
x3 x1
y3 y1
z3 z1
Если совместить точку М1 с началом координат то определитель упроститься
x
y
z
x2
y2
z2 0
x3
y3
z3
Для составления уравнения плоскости можно использовать определитель
третьего порядка, который можно посчитать по формуле разложения по строке.
8.
Нахождение определителя.Определителем квадратной матрицы называется число, которое может быть
вычислено по элементам матрицы по формуле разложения по первой строке:
n
(-1) k 1a1k M 1k
k 1
где М1к – детерминант матрицы, полученной из исходной вычеркиванием
первой строки и k – го столбца.
Для матрицы второго порядка определитель вычисляется по формуле:
a11
a12
a21 a22
a11a22 a12a21
Для матрицы третьего порядка определитель вычисляется по формуле:
a11
a12
a13
a 21
a 22
a 23 a11 ( 1)1 1
a 31
a 32
a 33
a 22
a 23
a 32
a 33
a12 ( 1)1 2
a 21
a 23
a 31
a 33
a13 ( 1)1 3
a11 ( a 22 a 33 a 23a 32 ) a12 ( a 21a 33 a 23a 31 ) a13 ( a 21a 32 a 22 a 31 )
a 21
a 22
a 31
a 32
9.
Пример нахождения уравнения плоскости и вектора нормали.Заданы точки:
нормали.
x
y
z
0
1 0,5 x
1
0
1
A(0;0;0) , B (0;1;0,5)
1 0,5
0
1
y
0 0,5
1
1
z
,
C (1;0;1)
0 1
1 0
найдем уравнение плоскости и вектор
x (1 0) y (0 0,5) z (0 1) x 0,5 y z
x 0,5 y z 0 - уравнение плоскости проходящее через точки А, В, С.
Вектор нормали
n{1;0,5; 1}
10.
Угол между нормалями в координатной форме.После того, как мы нашли координаты векторов нормалей двух плоскостей, угол
между двумя пересекающимися плоскостями можно вычислить как угол между
нормалями по формуле:
cos
где n1{A1 ; B1 ; C1}
n2 {A2 ; B2 ; C2 }
A1 A2 B1 B2 C1C2
A , B C A B C
2
1
2
1
2
1
2
2
2
2
2
2
,
- вектор
нормали плоскости A1x B1y C1z D1 0
- вектор
нормали плоскости A2 x B2 y C2 z D2 0
11.
Алгоритм решения задач на нахождение угла между плоскостями:1. На рисунке изображаем указанные в задаче плоскости
2. Вписываем фигуру в систему координат
4. Находим уравнения заданных плоскостей
5. Находим координаты вектора нормали к плоскостям
6. Подставляем в формулу "косинус угла между плоскостями"
7. После чего (если требуется в задаче), зная косинус, находим значение
самого угла.
Для того, чтобы лучше понять алгоритм решения данных типов задач,
лучше рассмотреть решение самых простых из них.
Ниже будут приведены решения именно таких заданий.
12.
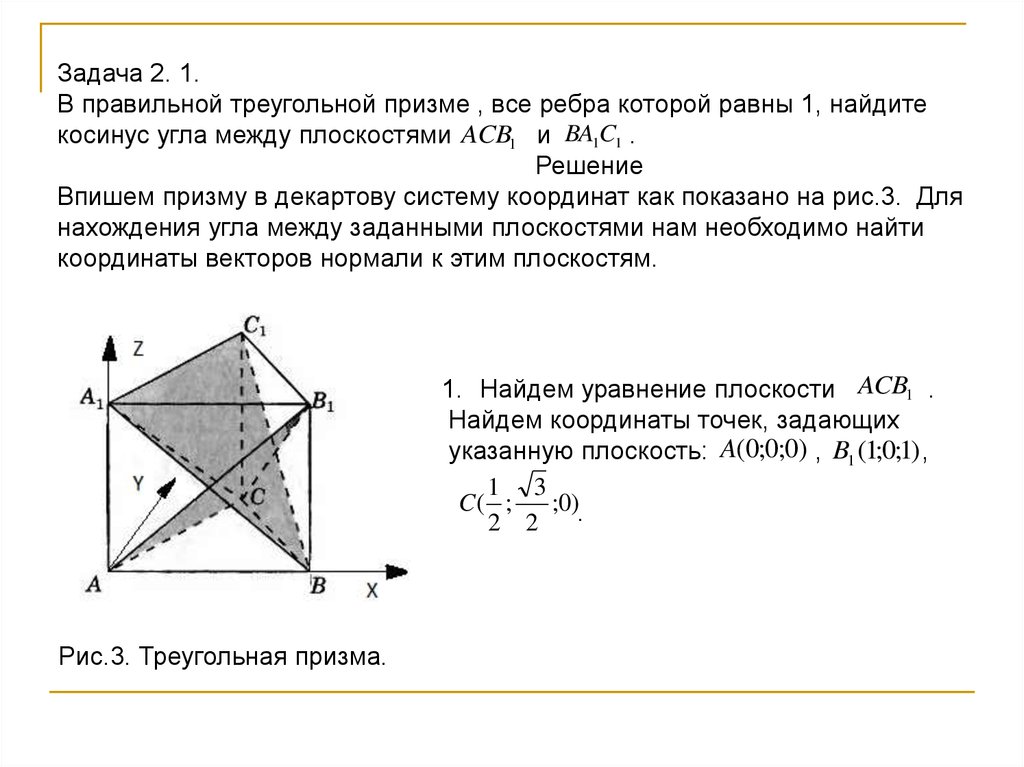
Задача 2. 1.В правильной треугольной призме , все ребра которой равны 1, найдите
косинус угла между плоскостями ACB1 и BA1C1 .
Решение
Впишем призму в декартову систему координат как показано на рис.3. Для
нахождения угла между заданными плоскостями нам необходимо найти
координаты векторов нормали к этим плоскостям.
1. Найдем уравнение плоскости ACB1 .
Найдем координаты точек, задающих
указанную плоскость: A(0;0;0) , B1 (1;0;1) ,
1 3
C( ;
;0).
2 2
Рис.3. Треугольная призма.
13.
Найдем уравнение плоскости.x
y
1
0
3
2
0,5
z
0
1 x 3
2
0
1
0
y
1
1
0,5 0
z
1
0
3
3
) y (0 0,5) z (
0)
3 x (0
2
2
2
0,5
3
3
x 0,5 y
z 0
2
2
Умножив каждое слагаемое на (-2) получим уравнение плоскости:
3x - y - 3z 0
n1{ 3; 1; 3}
n1
2
3 ( 1) 2 ( 3) 2 7
14.
2. Найдем уравнение плоскости BA1C1 . Найдем координаты точек, задающих1 3
указанную плоскость: A1 (0;0;1) , B(1;0;0) , C1 ( ; ;1)
2 2
Найдем уравнение плоскости.
x x1
y y1
z z1
x 2 x1
y 2 y1
z 2 z1 1 0
x3 x1
y 3 y1
z 3 z1
x
y
z -1
1
0
3
2
0,5
0
-1 x 3
2
0
1
0
x 0
y
0,5 0
1
1
0,5
0
Получили уравнение плоскости
n2 { 3;1; 3}
y 0
z 1
x
0 0 0 1 1
3
0 1 1 0,5
2
( z 1)
1
0,5
2
0
3
2
z -1
-1 0
0
0
3
3
3
x 0,5 y
z
0
3
2
2
2
2
3x y 3 3 0
n2
y
2
3 1 3 7
2
15.
3. Найдем косинус угла между заданными плоскостями.n n
A A B B C1C 2
cos 1 2 1 2 1 2
n1 n 2
n1 n 2
Ответ: cos
1
.
7
3 3 ( 1) 1 3 3
7 7
1
7
16.
3. Нахождение угла между прямой и плоскостью.Прежде чем переходить к алгоритму решения данного типа заданий вспомним,
что же является углом между прямой и плоскостью.
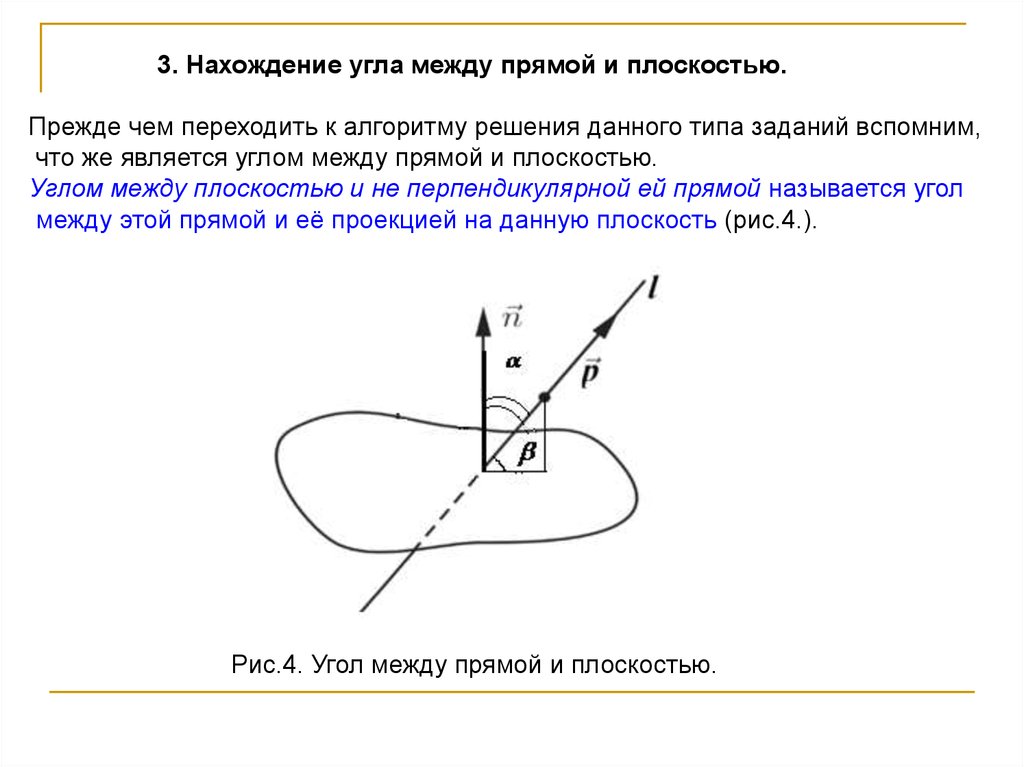
Углом между плоскостью и не перпендикулярной ей прямой называется угол
между этой прямой и её проекцией на данную плоскость (рис.4.).
Рис.4. Угол между прямой и плоскостью.
17.
На прямой можем выделить вектор, и найти его координаты:Нормаль можем провести к точке пересечения прямой
Вектор нормали будет иметь следующие координаты:
Тогда можем найти
n p
cos
n p
Из рисунка видно, что
Т.е получили
2
n p
sin
n p
,но нам нужен
значит
p{x 1 ; y1 ; z1}
и плоскости.
n{ A; B; C}
cos
cos cos(
2
) sin
A x1 B y1 C z1
A2 B 2 C 2 x12 y12 z12
18.
Алгоритм решения задач на нахождение угла между прямой иплоскостью:
1. На рисунке изображаем указанные в задаче прямую и плоскость (прямой
придаем направление, т.е. вектор)
2. Вписываем фигуру в систему координат
3. Находим координаты концов направляющего вектора.
4. Находим координаты вектора
5. Находим координаты вектора нормали к плоскости
6. Подставляем в формулу "синус угла между прямой и плоскостью"
7. После чего (если требуется в задаче), зная синус, находим значение
самого угла.
19.
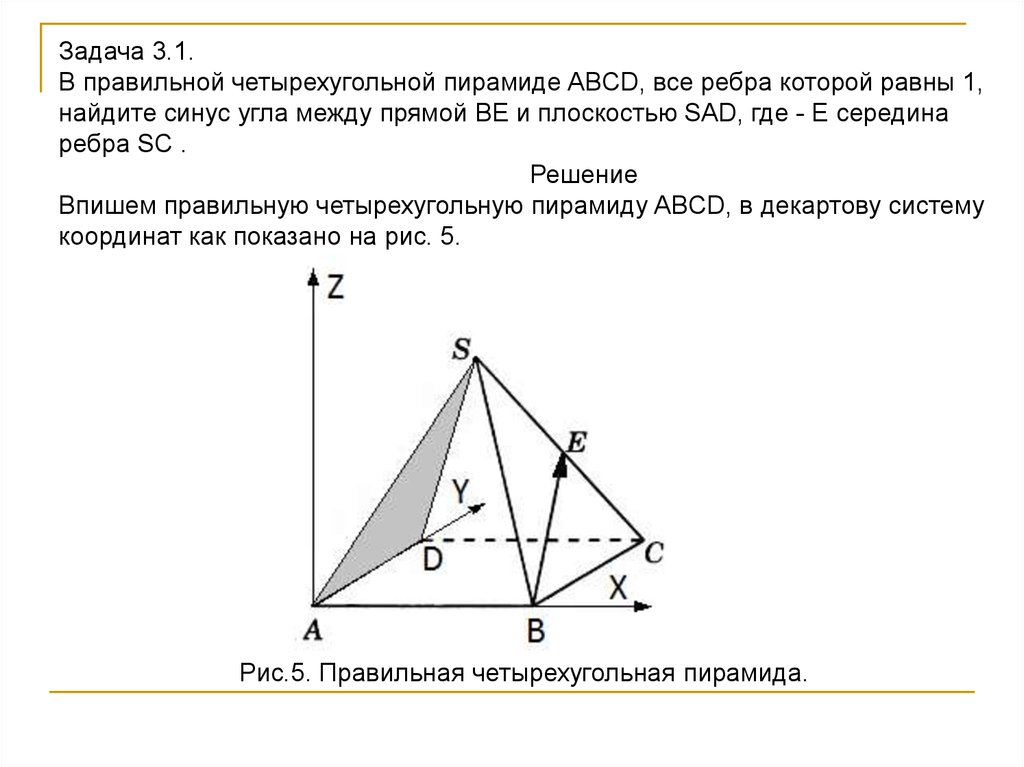
Задача 3.1.В правильной четырехугольной пирамиде ABCD, все ребра которой равны 1,
найдите синус угла между прямой BE и плоскостью SAD, где - E середина
ребра SC .
Решение
Впишем правильную четырехугольную пирамиду ABCD, в декартову систему
координат как показано на рис. 5.
Рис.5. Правильная четырехугольная пирамида.
20.
Для нахождения угла между заданной прямой и плоскостью нам необходимонайти координаты вектора принадлежащего прямой BE и координаты нормали
плоскости SAD.
1. Найдем уравнение плоскости и координаты вектора нормали.
Найдем координаты точек, задающих указанную плоскость:
1 1 2
S( ; ;
)
2 2 2
x
y
z
0
1
0 x
0,5
2
2
0,5 0,5
1
A(0;0;0)
0
0
2 y
0,5
2
2
1
x z 0
2
2
D(0;1;0)
0
0
1
2
2
x(
0) y (0 0) z (0 0,5)
x 0,5z
2 z
0,5 0,5
2
2
2
2
1
n{ ;0; }
2
2
2
1
3
n ( ) 2 02 ( ) 2
2
2
2
21.
2. Найдем координаты вектораBE
т.к
3 3 2
B(1;0;0) E ( ; ; )
4 4 4
1 2
3 2
2 2
12
BE ( ) ( ) ( )
4
4
4
4
1 3 2
BE{ ; ; }
4 4 4
3. Найдем синус угла между прямой и плоскостью.
.
sin
A x 1 B y1 C z1
A B C x y z
2
Ответ:
2
2
2
sin
3
2
1
2
1
2
1
2
1
3
1
2
( ) 0 ( )
2
4
4
2 4
3 12
2
4
2 2
2
8
3
3
4
22.
4. Нахождение расстояния от точки до плоскости.Для начала выясним, что называется расстоянием от точки до плоскости.
Расстояние от точки до плоскости, не содержащей эту точку, есть длина
отрезка перпендикуляра, опущенного из этой точки на плоскость (рис.6.) .
Рис.6. Расстояние от точки до плоскости.
23.
Итак, для того, чтобы найти расстояние от точки до плоскости нам необходимонайти координаты точки, и координаты нормали данной плоскости. После чего
воспользоваться следующей формулой:
d
( x0 ; y 0 ; z 0 )
Ax0 By 0 Cz0 D
A2 B 2 C 2
- координаты заданной точки
Ax By Cz D 0
- уравнение плоскости
, где
24.
Алгоритм решения задач на нахождение расстояния от точкидо плоскости:
1. На рисунке отмечаем указанные в задаче точку и плоскость.
2. Вписываем фигуру в систему координат.
3. Находим координаты точек (данной и трех точек плоскости).
4. Составляем уравнение плоскости .
5. Находим координаты вектора нормали плоскости.
6. Подставляем в формулу "расстояние от точки до плоскости"
25.
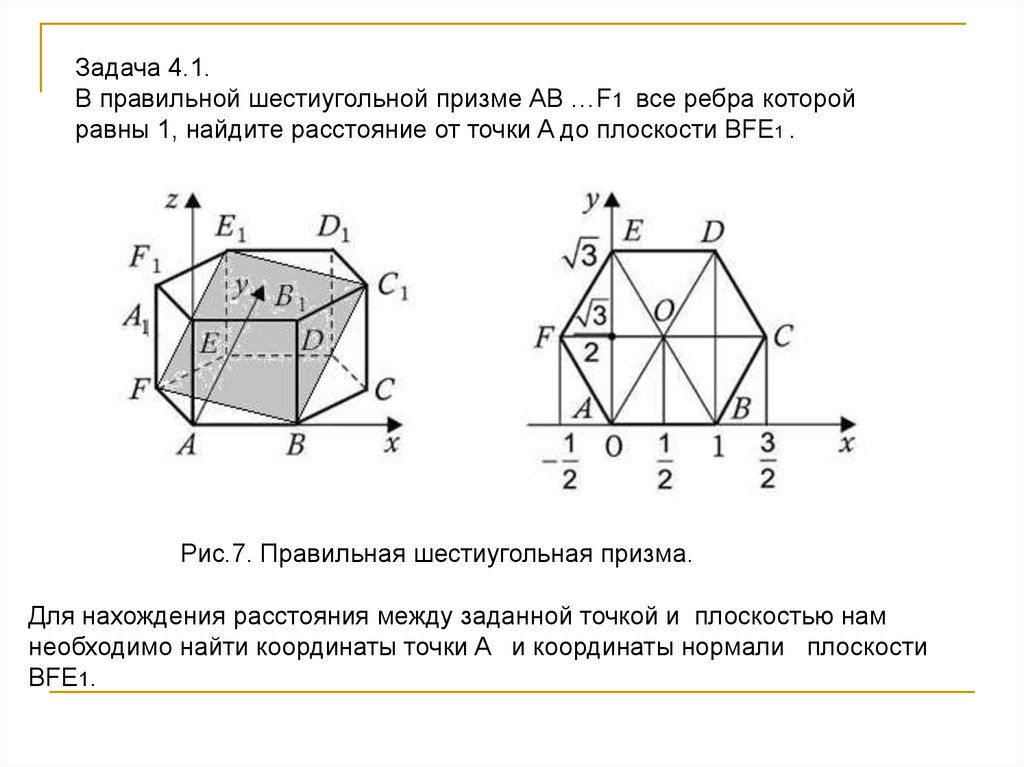
Задача 4.1.В правильной шестиугольной призме АВ …F1 все ребра которой
равны 1, найдите расстояние от точки A до плоскости BFE1 .
Рис.7. Правильная шестиугольная призма.
Для нахождения расстояния между заданной точкой и плоскостью нам
необходимо найти координаты точки A и координаты нормали плоскости
BFE1.
26.
1. Найдем уравнение плоскости BFE1. Найдем координаты точек, задающихуказанную плоскость:
B(1;0;0)
1 3
F ( ;
;0)
2 2
E1 (0; 3;1)
Воспользовавшись понятием определителя найдем уравнение плоскости.
x 1
1
- -1
2
0 1
y-0
z - 0 x 1
3
1
0 0 - 0 1
2
2
3 0 1 0
1
y
3
2
3
z
3
0 ( x 1) 2
3
1
1
y
2
1
1
0
1
1
z
2
1
1
0
1
3
1
3 3
3
3
3
1
0) y ( 1 0) z (
(
))
x
1 y 3z
2
2
2
2
2
2
2
Получили уравнение плоскости:
( x 1)(
3 x 3 y 2 3z 3 0
n{ 3;3; 2 3}
n ( 3 ) 2 32 ( 2 3 ) 2 24
3
2
3
27.
2. Координаты точки А(0,0,0).3. Расстояние от точки А до плоскости BFE1 находим по формуле:
d
Ax0 By 0 Cz0 D
A2 B 2 C 2
Ответ: d
2
4
3 0 3 0 ( 2 3 ) 0 3
24
3
1
1
2
8 2 2
4
24
28.
5. Заключение.Решение вышеприведенных задач показывает возможность совместного
применения координатно – векторного метода и понятия определителей
для упрощения вычислений и экономии времени.
29.
Литература1. В.В.Леваков Решение заданий С2 ЕГЭ по
математике координатно-векторным методом.
2. Л.С.Атанасян Геометрия 10 -11класс























 Математика
Математика








