Подготовка к ЕГЭ. Решение задач С2

1. Подготовка к ЕГЭ. Решение задач С2.

Коткова Евгения Сергеевна,
учитель математики
МБОУ «Лицей № 83» г. Казани,
I квалификационная категория

2. Типы задач С2

Расстояние между двумя точками
Расстояние от точки до плоскости
Угол между прямой и плоскостью
Угол между плоскостями

3. Расстояние между двумя точками

Пусть точки A( x1 , y1 , z1 ) и B( x 2 , y 2 , z 2 ) концы отрезка АВ. Тогда внутренняя точка
С отрезка АВ такая, что АС:СВ=k, имеет
координаты
x1 kx 2 y1 ky 2 z1 kz 2
С
,
,
k 1
k 1
k 1

4.

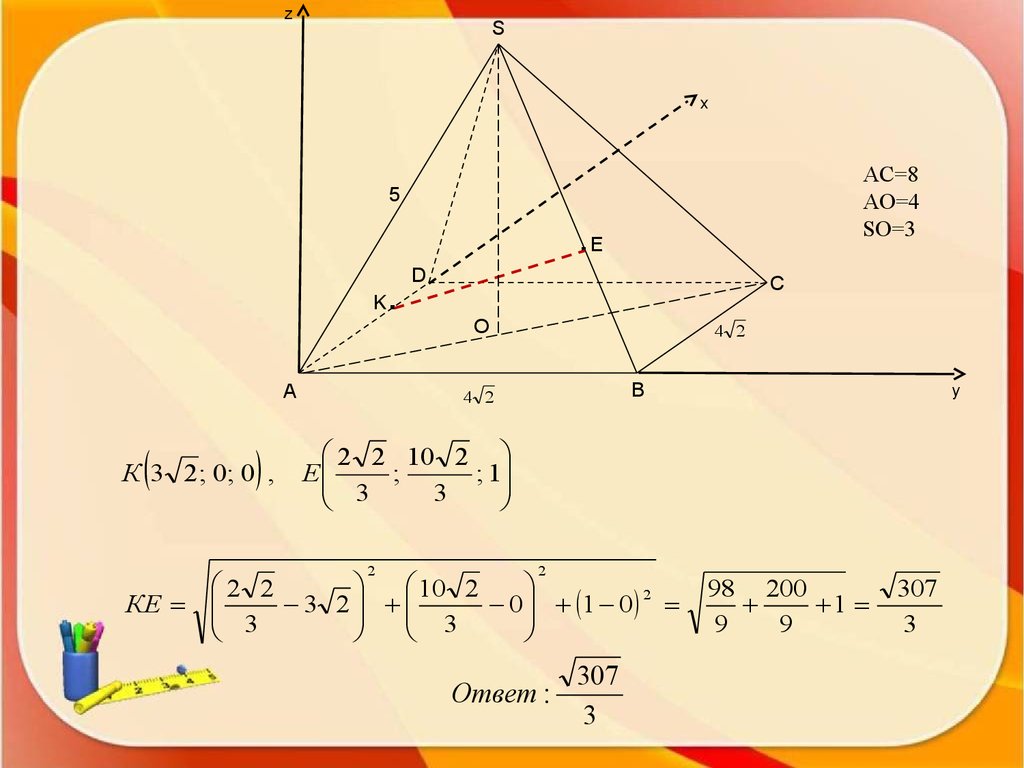
Задача. В правильной четырехугольной пирамиде SABCD, сторона
4 2
основания
и боковое ребро которой равны
и 5 соответственно.
Найдите
z
расстояние
между
точками Е и К, если известно, что Е
S
лежит на
боковом ребре SB и SE=2BE, а К – на стороне основания AD и
x
AC=8
AK=3KD.
AO=4
SO=3
5
.E
.
D
С
K
А
B 0; 4
2 ; 0 , S 2
К 3 2 ; 0; 0
O
4 2
В
4 2
y
2 ; 2 2 ; 3 по формуле находим координаты точки Е :
2 2 2 0 2 2 2 4 2 3 2 0 2 2 10 2
Е
;
;
;
; 1
2 1
2 1
2 1 3
3

5.

z
S
x
AC=8
AO=4
SO=3
5
.E
.
D
С
K
А
К 3 2 ; 0; 0 ,
4 2
В
4 2
y
2 2 10 2
Е
;
; 1
3
3
2
КЕ
O
2
2 2
10 2
1 0 2
3
2
0
3
3
Ответ :
307
3
98 200
1
9
9
307
3

6. Расстояние от точки до плоскости

Координатный метод
Расстояние от точки М ( x0 , y 0 , z 0 ) до плоскости ,
заданной уравнением ax+by+cz+d=0, можно
вычислить по формуле
M ,
ax 0 by 0 cz 0 d
a2 b2 c2

7.

Задача (ЕГЭ, 2012). В правильной треугольной призме ABCA
1B1C1 стороны
основания равны 2, боковые рёбра равны 3, точка D –
середина ребра CC1. Найдите расстояние от вершины
С до плоскости ADB1.
z
Решение:
А1
В1
3
О
А
2
y
В
A 0; 0; 0 ,
B1 1;
3; 3 ,
3
D 2; 0;
2
Подставим координаты точек в уравнение плоскости
ax+by+cz+d=0,
С1
d 0,
d 0,
a
3
b
3
c
0
,
b 3a,
3
4
.D
2a c 0.
c a.
2
3
4
a x 3a y a z 0 3 x 3 3 y 4 z 0
3
x
С
a 3 , b 3 3 , c 4 , d 0 ,
C 2; 0; 0
Вычислим расстояние от точки С до плоскости ADB1 по формуле:
С , ADB1
2 3 3 3 0 4 0 0
9 27 16
Ответ :
3 13
13
6
52
3 13
13

8. Угол между прямой и плоскостью

Векторно - координатный метод
Угол между прямой ℓ и плоскостью α можно вычислить по формуле
n p
sin
n p
где
x1 x 2 y1 y 2 z1 z 2
2
2
2
2
2
x1 y1 z1 x 2 y 2 z 2
2
n x1 , y1 , z1 вектор нормали плоскости ,
p x 2 , y 2 , z 2 направляющий вектор прямой .
,

9.

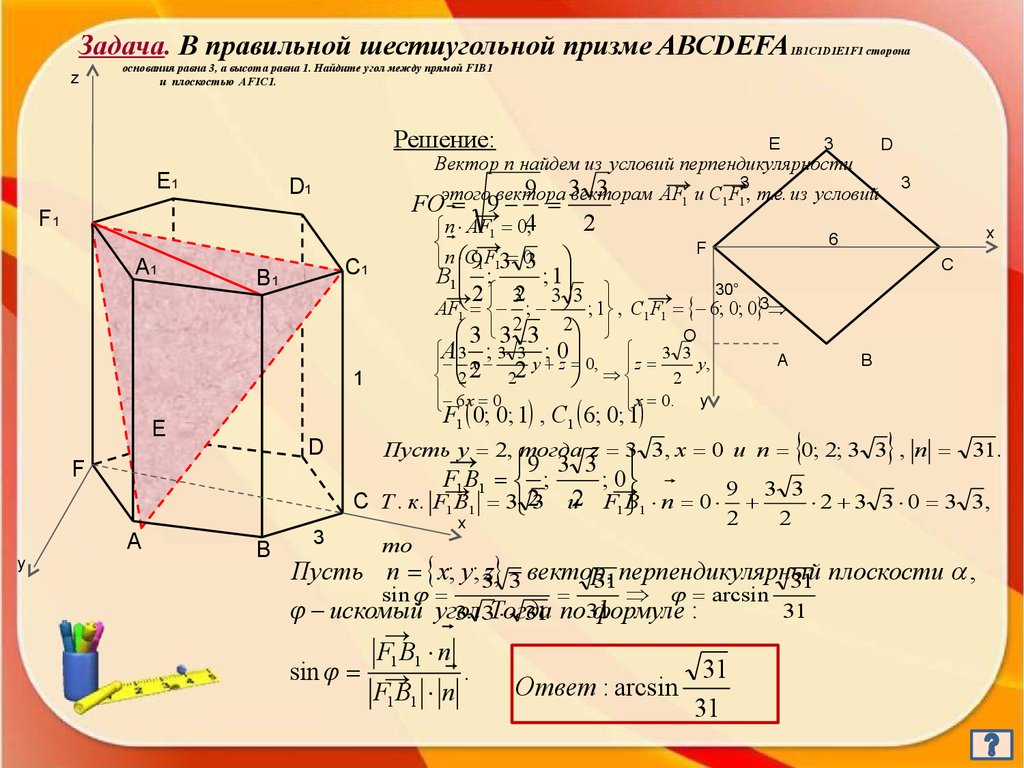
Задача. В правильной шестиугольной призме ABCDEFA
z
1B1C1D1E1F1 сторона
основания равна 3, а высота равна 1. Найдите угол между прямой F1B1
и плоскостью AF1C1.
Решение:
E1
E
3
D
Вектор n найдем из условий перпендикулярности
3
3
→ и C→
9 3векторам
3
этого вектора
AF
1
1 F1 , т.е. из условий
FO →
9
4
2
n
AF
1 0,
6
→
F
n
C
F
0
91 13 3
D1
F1
А1
С1
В1
B1 ;
; 1
30°
2
2
3 3 3
→
→
AF1 ;
; 1 , C1 F1 6; 0; 0 3
3 32 3 2
O
A 3 ; 3 3 ; 0
3 3
x 2 y z
y,
0, z
2
2
2
2
1
D
F
А
x 0.
F1 0; 0; 1 , С1 6; 0; 1
E
y
6 x 0
В
3
А
x
С
В
y
31.
9 3 3
F
;→
0
1 B1 ;
9 3 3
→
2
2
С Т . к. F1 B1 3 3 и F1 B
1 n 0 2 2 2 3 3 0 3 3 ,
Пусть y 2, тогда z 3 3 , x 0 и n 0; 2; 3 3 , n
→
x
то
Пусть n x; y; 3z 3 вектор31, перпендикулярный
31 плоскости ,
sin
arcsin
31
искомый угол
формуле :
3 .3Тогда
31 по 31
→
F1 B1 n
31
sin → .
Ответ
:
arcsin
F1 B1 n
31

10. Угол между плоскостями

Векторно - координатный метод
Задачу о нахождении угла между плоскостями α и β, заданными в
прямоугольной системе координат уравнениями p x+q y+r z+d =0 и
p x+q y+r z+d =0 соответственно, удобнее свести к задаче о нахождении
угла между векторами их нормалей
n p1 , q1 , r1 и n p 2 , q 2 , r2 , используя формулу
n n
p1 p 2 q1 q 2 r1 r2
cos ( , )
2
2
2
2
2
2
n n
p1 q1 r1 p 2 q 2 r2
1
2
2
2
2
1
1
1

11.

Задача (ЕГЭ, 2012). В правильной четырёхугольной призме ABCDA
1B1C1D1
стороны основания равны 2, а боковые рёбра равны 5.
На ребре АА1 отмечена точка Е так, что АЕ:ЕА1=3:2.
Найдите угол между плоскостями АВС и BED1.
z
D1
С1
А1
E
В1
5
.
D
А
y
С
2
В
x
Решение: Составим уравнение плоскости BED1.
В(2;0;0), Е(0;0;3), D1(0;2;5)
.
Итак, n1 координаты
3; 2; 2 , nточек
Подставим
в; 1уравнение
плоскости
2 0; 0
ax+by+cz+d=0,
Используя формулу , вычислим
1косинус искомого угла :
c 3 d ,
3c d 0,
n1 n2
0 0 2
2
2 17
1
cos
(
ABC
,
BED
)
a d ,
2a d 0, 1
n n
17
17
2a 5c d 0. 1 2 20 0 1 9 4 4
1
2 17
b darccos
.
Отсюда искомый угол равен
.
3
17
1
1
1
dx dy dz d 0
2
3
3
3x 2 y 2 z 6 0 уравнение2плоскости
17
Ответ
:
arccos
Координаты нормальног о вектора n1 . 3; 2; 2 .
17
Т. к. ось Аz перпендикулярна плоскости основания, то
нормальный вектор плоскости АВС имеет координаты n 2 0; 0;1

12.

Спасибо за внимание!

13.

Расстояние между двумя точками
Пусть точки A( x1 , y1 , z1 ) и B( x 2 , y 2 , z 2 ) концы отрезка АВ. Тогда внутренняя точка
С отрезка АВ такая, что АС:СВ=k, имеет
координаты
x1 kx 2 y1 ky 2 z1 kz 2
С
,
,
k 1
k 1
k 1

14. Расстояние от точки до плоскости

Координатный метод
Расстояние от точки М ( x0 , y 0 , z 0 ) до плоскости ,
заданной уравнением ax+by+cz+d=0, можно
вычислить по формуле
M ,
ax 0 by 0 cz 0 d
a2 b2 c2

15. Угол между прямой и плоскостью

Векторно - координатный метод
Угол между прямой ℓ и плоскостью α можно вычислить по формуле
n p
sin
n p
где
x1 x 2 y1 y 2 z1 z 2
2
2
2
2
2
x1 y1 z1 x 2 y 2 z 2
2
n x1 , y1 , z1 вектор нормали плоскости ,
p x 2 , y 2 , z 2 направляющий вектор прямой .
,

16. Угол между плоскостями

Векторно - координатный метод
Задачу о нахождении угла между плоскостями α и β, заданными в
прямоугольной системе координат уравнениями p x+q y+r z+d =0 и
p x+q y+r z+d =0 соответственно, удобнее свести к задаче о нахождении
угла между векторами их нормалей
n p1 , q1 , r1 и n p 2 , q 2 , r2 , используя формулу
n n
p1 p 2 q1 q 2 r1 r2
cos ( , )
2
2
2
2
2
2
n n
p1 q1 r1 p 2 q 2 r2
1
2
2
2
2
1
1
1