Движения. Центральная симметрия

1. Движения

2.

Преобразование одной фигуры в
другую, при котором сохраняется
расстояние между точками называется
движением.

3.

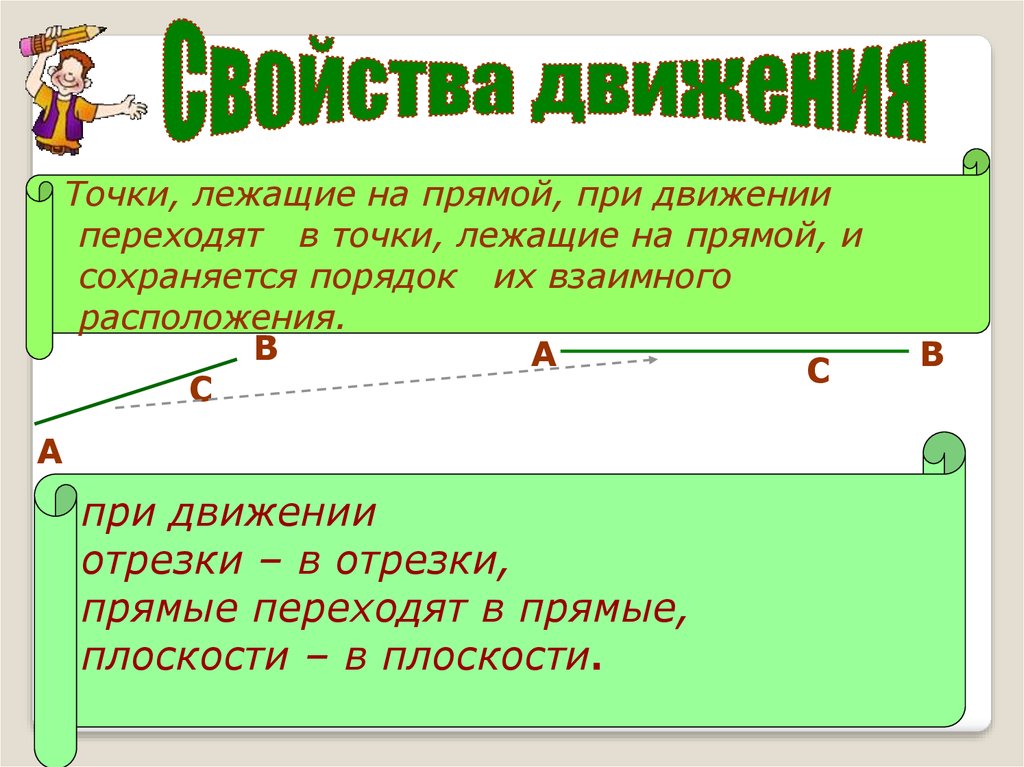
Точки, лежащие на прямой, при движении
переходят в точки, лежащие на прямой, и
сохраняется порядок их взаимного
расположения.
В
А
С
С
А
при движении
отрезки – в отрезки,
прямые переходят в прямые,
плоскости – в плоскости.
В

4.

Центральная
симметрия
Поворот
Осевая симметрия
Параллельный
перенос

5.

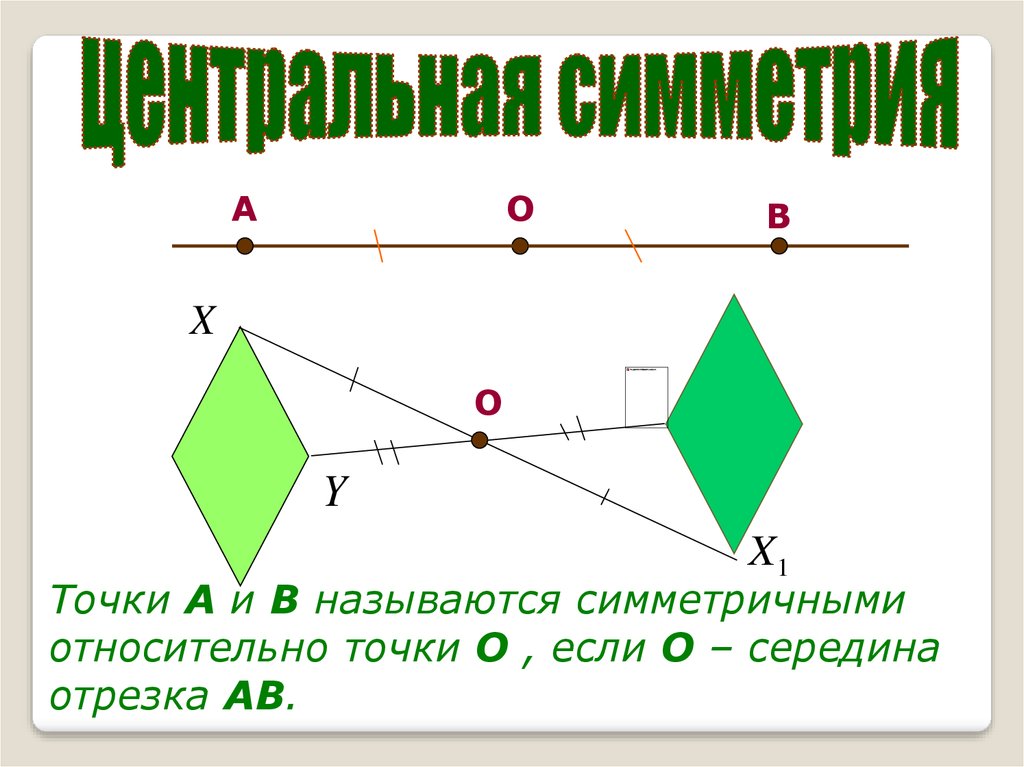
А
О
В
X
О
Y
X1
Точки А и В называются симметричными
относительно точки О , если О – середина
отрезка АВ.

6.

ДОКАЖЕМ, ЧТО ЦЕНТРАЛЬНАЯ СИММЕТРИЯ,
ЕСТЬ ДВИЖЕНИЕ (прочитайте стр.121-122)
Z
В
A1
А( x1; y1; z1 )
А
B ( x 2 ; y2 ; z2 )
А1 ( x1 ; y1 ; z1 )
B1 ( x 2 ; y2 ; z 2 )
У
Х
В1
АB ( х 2 х1 ) 2 ( у 2 у1 ) 2 ( z 2 z1 ) 2
АB A1 B1

7.

Фигура называется центрально симметричной
относительно точки О, если для каждой точки
фигуры симметричная ей точка также
принадлежит этой фигуре.
Точка О называется центром симметрии
фигуры. Говорят также, что фигура обладает
центральной симметрией.
О
О

8.

9.

Укажите координаты точек А1;
В1; С1; К1 симметричных точкам
А; В; С; К относительно начала
координат, если:
А(3; -7; 1)
А1 (-3; 7; -1)
В(-4; 0; 8)
В1 (4; 0; -8)
С(1,3; -5; -0,7)
С1 (-1,3; 5; 0,7)
К( -1; 5,6; 7,1)
К1 (1; -5,6; -7,1)

10. Осевая симметрия

Осевая симметрия- отображение пространства на себя,
при котором любая точка переходит в симметричную ей
точку, относительно оси а.
А
а
А1
Две точки А и А1 называются симметричными
относительно прямой а, если а серединный
перпендикуляр к отрезку АА1

11.

12.

ДОКАЖЕМ, ЧТО ОСЕВАЯ СИММЕТРИЯ, ЕСТЬ
ДВИЖЕНИЕ (прочитайте стр 122)
OZ
Z
В1
А( x1; y1; z1 ) А1 ( x1; y1; z1 )
В
A1
А
B ( x 2 ; y2 ; z2 )
B1 ( x 2 ; y2 ; z2 )
У
Х
АB ( х 2 х1 ) 2 ( у 2 у1 ) 2 ( z 2 z1 ) 2
А1 B1 ( х2 х1 ) 2 ( у2 у1 ) 2 ( z2 z1 ) 2
АB A1 B1

13.

Фигура называется симметричной относительно
прямой а, если для каждой точки фигуры симметричная
ей точка относительно прямой а также принадлежит
этой фигуре. Прямая а называется осью симметрии
фигуры.
Говорят также, что фигура обладает осевой
симметрией.

14.

Укажите координаты точек А1;В1; С1;
симметричных точкам А; В; С;
относительно осей ОХ и ОУ если:
ОХ
ОУ
А(3; -7; 1) А1 (3; 7; -1)А1 (-3; -7; -1)
В1 (4; 0; -8)
В(-4; 0; 8) В1 (-4; 0; -8)
С
(-1,3;-5;7)
С
(1,3;5;7)
1
С(1,3; -5;-7) 1