Переменный ток

1. Переменный ток

Лекция 3

2. Переменный ток -

Переменный ток ,
ток, изменяющийся во времени) по
величине и направлению
(по синусоидальному закону).
Период (Т) - Наименьший промежуток времени,
через который периодически изменяющаяся
величина повторяется по форме и величине
f
f .
Мгновенное значение- значение синусоидально
изменяющейся функции в любой момент
времени
a(t)=Amsin( t + )
Am – максимальное значение, или амплитуда (Im);
t+ – фаза (фазовый угол);
– начальная фаза (начальный фазовый угол);
– угловая частота.

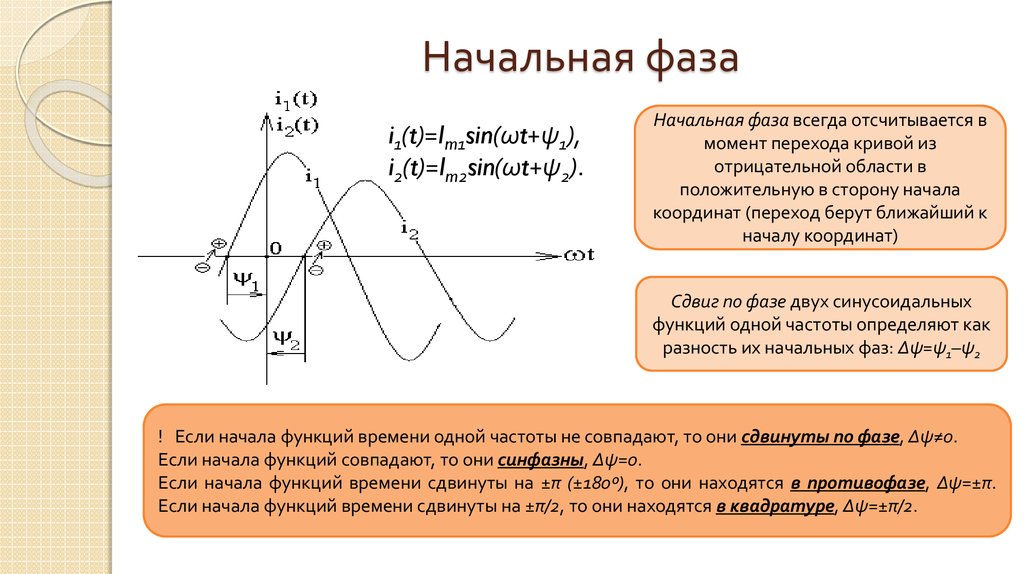
3. Начальная фаза

i1(t)=Im1sin(ωt+ψ1),
i2(t)=Im2sin(ωt+ψ2).
Начальная фаза всегда отсчитывается в
момент перехода кривой из
отрицательной области в
положительную в сторону начала
координат (переход берут ближайший к
началу координат)
Сдвиг по фазе двух синусоидальных
функций одной частоты определяют как
разность их начальных фаз: Δψ=ψ1–ψ2
! Если начала функций времени одной частоты не совпадают, то они сдвинуты по фазе, Δψ≠0.
Если начала функций совпадают, то они синфазны, Δψ=0.
Если начала функций времени сдвинуты на ±π (±180º), то они находятся в противофазе, Δψ=±π.
Если начала функций времени сдвинуты на ±π/2, то они находятся в квадратуре, Δψ=±π/2.

4.

Действующие значения переменных токов, напряжений, э.д.с:
T
1 2
I
i (t )d t
T0
Средние значения переменных токов, напряжений, э.д.с за
положительную полуволну:
T
I СР
1 2
i (t )d t
T 0
2

5. Изображение функции комплексным числом Записи комплексного числа.

a A cos Re A
b A sin Im A
A a2 b2
b
arctg
a
j 1 e
j
2

6. Действия над комплексными числами

Алгебраическая форма
Показательная форма
A B Ae j a Be j b ABe j a b
A Ae j a
A j a b
e
j b
B
B Be
A Ae
j a n
n
n
A n e jn a A n cos n a jAn sin n a
1
n
A n Ae j a A e
A e j A cos j sin
j
a
n

7. Элементы цепи переменного тока

Элемент
Свойства
Резистор
Эл.
сопротивление
Индуктивная
Индуктивность
катушка
Конденсатор
Емкость
Обозначение
R
L
C
Сопротивление
R
xL= L
xC =1/ C
Запись
в комплексной форме
R
ZL= j L
Проводимость
Проводимость
в комплексной
форме
g = 1/R
g = 1/R
YL=1/ZL=
= – jbL
YC=1/ZC=
= jbC

8. Закон Ома

U
I
Z
Z – комплексное сопротивление участка цепи
Z = R+j(xL–xC)

9. Законы Кирхгофа

10. Мощность в цепи синусоидального тока

Мгновенная мощность:
p(t)= i(t)·u(t)= UmIm·sinωt·sin(ωt+φ)=UIcosφ–UIcos(2ωt+φ)
Полная мощность:
S U I UI cos jUI sin P jQ Se j
Баланс мощностей:
2
2
E
I
U
J
I
R
jI
k k
k
k
k k
k ( X Lk X Ck )
k 1
k 1
n
n

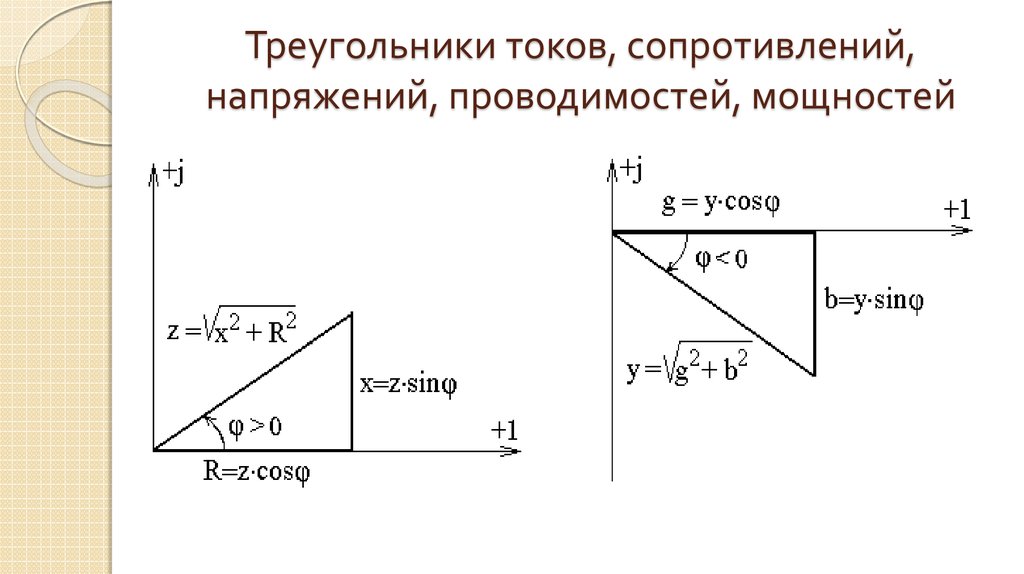
11. Треугольники токов, сопротивлений, напряжений, проводимостей, мощностей

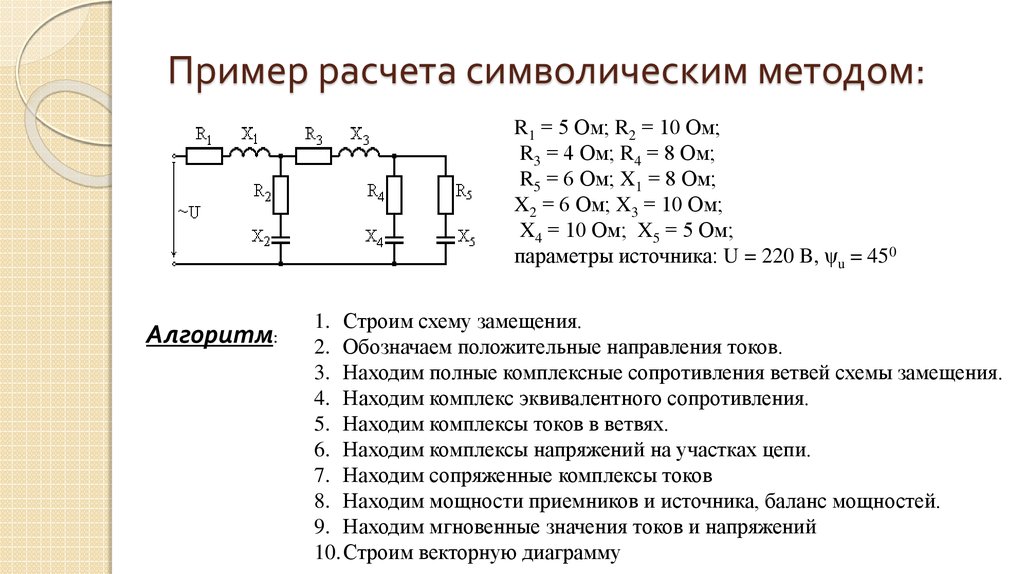
12. Пример расчета символическим методом:

R1 = 5 Ом; R2 = 10 Ом;
R3 = 4 Ом; R4 = 8 Ом;
R5 = 6 Ом; X1 = 8 Ом;
X2 = 6 Ом; X3 = 10 Ом;
X4 = 10 Ом; X5 = 5 Ом;
параметры источника: U = 220 B, ψu = 450
Алгоритм:
1. Строим схему замещения.
2. Обозначаем положительные направления токов.
3. Находим полные комплексные сопротивления ветвей схемы замещения.
4. Находим комплекс эквивалентного сопротивления.
5. Находим комплексы токов в ветвях.
6. Находим комплексы напряжений на участках цепи.
7. Находим сопряженные комплексы токов
8. Находим мощности приемников и источника, баланс мощностей.
9. Находим мгновенные значения токов и напряжений
10.Строим векторную диаграмму

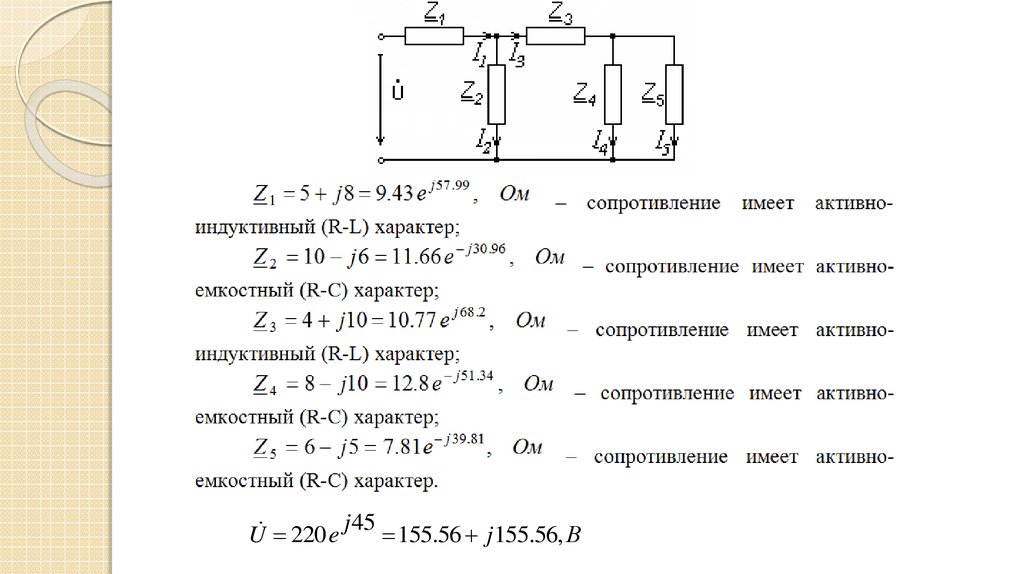
13.

j 45
U 220 e
155.56 j 155.56, В

14.

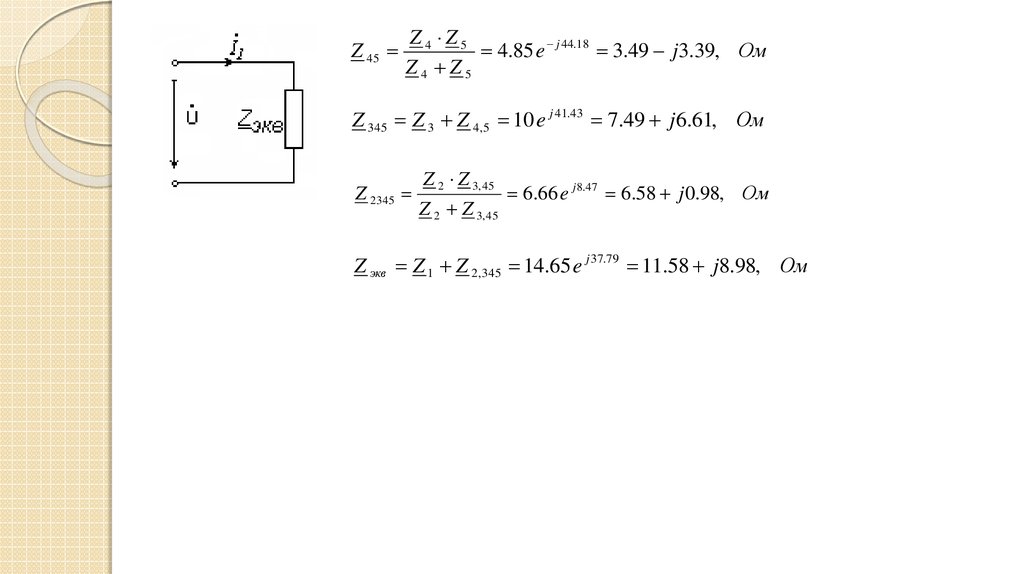
Z 45
Z4 Z5
4.85 e j 44.18 3.49 j 3.39, Ом
Z4 Z5
Z 345 Z 3 Z 4,5 10 e j 41.43 7.49 j 6.61, Ом
Z 2345
Z 2 Z 3, 45
Z 2 Z 3, 45
6.66 e j 8.47 6.58 j 0.98, Ом
Z экв Z 1 Z 2,345 14.65 e j 37.79 11.58 j8.98, Ом