Взаимное расположение прямой и плоскости

1.

Пусть прямая задана уравнением:
x x1 y y1 z z1
m
n
p
И пусть задана плоскость
Ax By Cz D 0
Рассмотрим возможные случаи ориентации
прямой и плоскости:

2.

1
Прямая принадлежит плоскости.
Тогда направляющий вектор прямой
s (m, n, p)
ортогонален нормальному вектору плоскости
n ( A, B, C )
И пусть точка
M 0 ( x0 , y0 , z0 )
принадлежит прямой.

3.

Тогда выполняются следующие условия:
Поскольку вектора
в
s
и
n
этом случае перпендикулярны, и их
скалярное произведение этих векторов
равно нулю:
(n, s ) Am Bn Cp 0
1
Поскольку точка М0 будет принадлежать
плоскости,
то
ее
координаты
удовлетворяют уравнению плоскости:
Ax0 By0 Cz 0 D 0
2

4.

2
Прямая параллельна плоскости.
Тогда выполняется только условие (1).
3
Прямая пересекает плоскость в одной точке.
Тогда выполняется условие
(n, s ) Am Bn Cp 0

5.

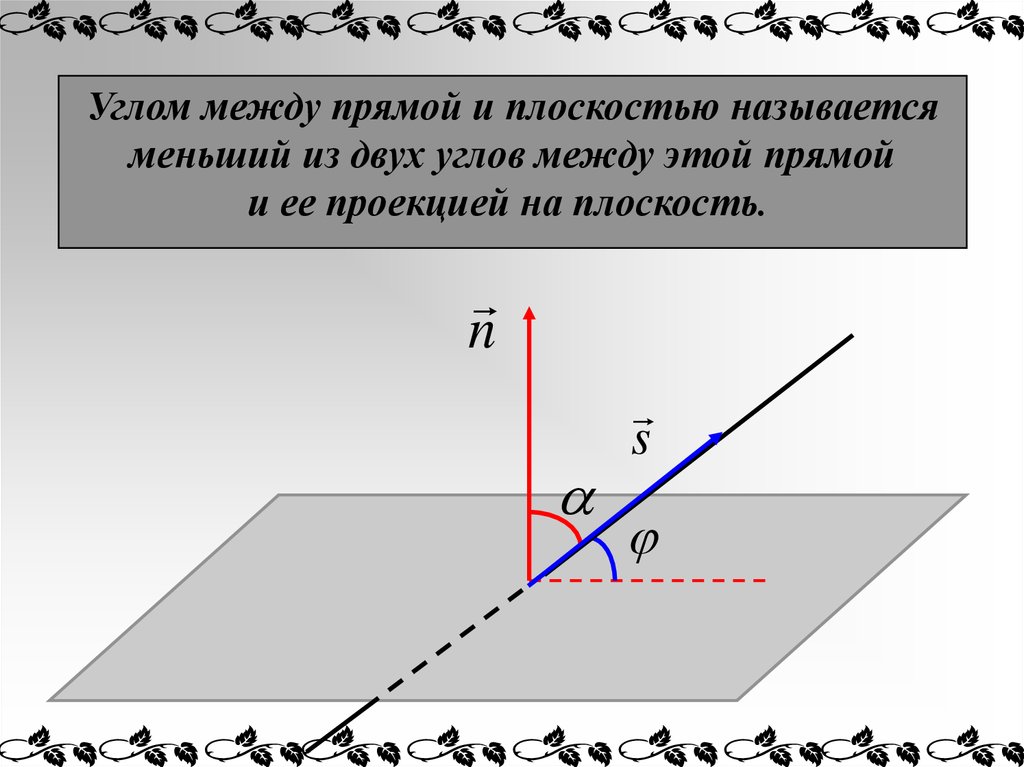
Углом между прямой и плоскостью называется
меньший из двух углов между этой прямой
и ее проекцией на плоскость.
n
s

6.

Синус угла φ между прямой и плоскостью
равен косинусу угла α между нормальным
вектором
плоскости
и
направляющим
вектором прямой:
sin cos
Найдем угол
векторами:
cos
α,
как
угол
между
двумя
Am Bn Cp
A B C
2
2
2
m n p
2
2
2

7.

sin
Am Bn Cp
A B C
2
2
2
m n p
2
2
2

8.

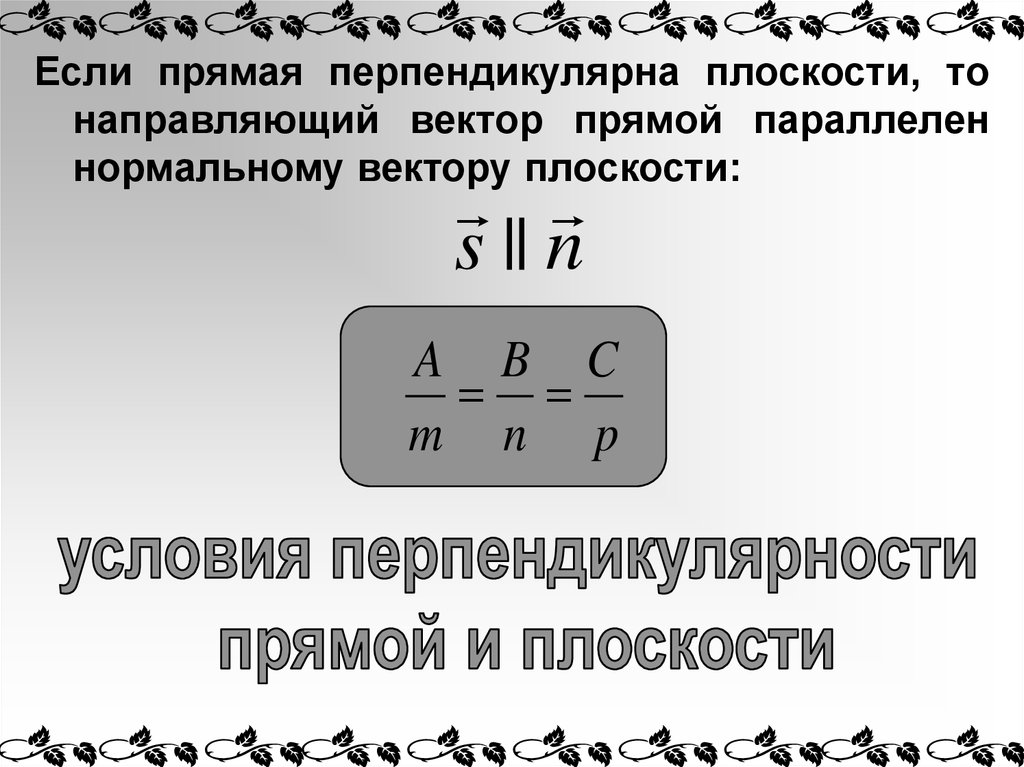
Если прямая перпендикулярна плоскости, то
направляющий вектор прямой параллелен
нормальному вектору плоскости:
s || n
A B C
m n p

9.

Если прямая параллельна плоскости, то
s n
Am Bn Cp 0