Похожие презентации:
Расчет коэффициентов регрессии (МНК)
1.
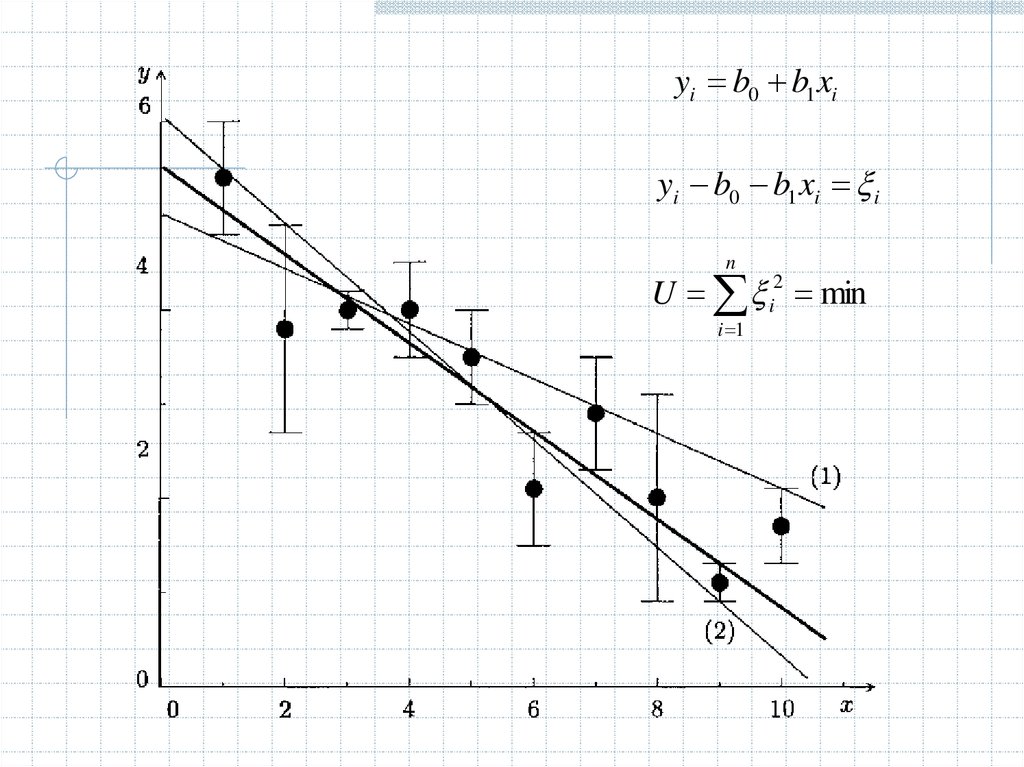
yi b0 b1 xiyi b0 b1 xi i
n
U i2 min
i 1
2. Расчет коэффициентов регрессии (МНК)
nn
U ( yi b0 b1 xi ) 2 min
i 1
2
i
i 1
dU
2 ( yi b0 b1 xi ) 0
db0
i 1
b0
n
n
y x y x x
i 1
i
i 1
2
i
i 1
i i
n
n x xi
i 1
i 1
n
2
i
i 1
2
i 1
i 1
n
n
b0 xi b1 x yi xi
dU
2 ( yi b0 b1 xi ) xi 0
db1
i 1
n
n
n
n
n
n
nb0 b1 xi yi
n
i
b1
2
i
i 1
i 1
i 1
n
n
n
i 1
i 1
i 1
2
n yi xi yi xi
n
n x xi
i 1
i 1
n
2
i
3.
Коэффициент корреляции Пирсонаn
R
cov x, y
x y
x
i 1
n
i
x yi y
n
2
x
x
y
y
i
i
i 1
2
i 1
Условия применения коэффициента корреляции Пирсона:
1. Переменные x и y должны быть распределены нормально.
2. Переменные x и y должны быть измерены в интервальной шкале
или шкале отношений.
3. Количество значений в исследуемых переменных x и y должно
быть одинаковым.
Значение коэффициента корреляции не зависит от масштаба
измерения.
4.
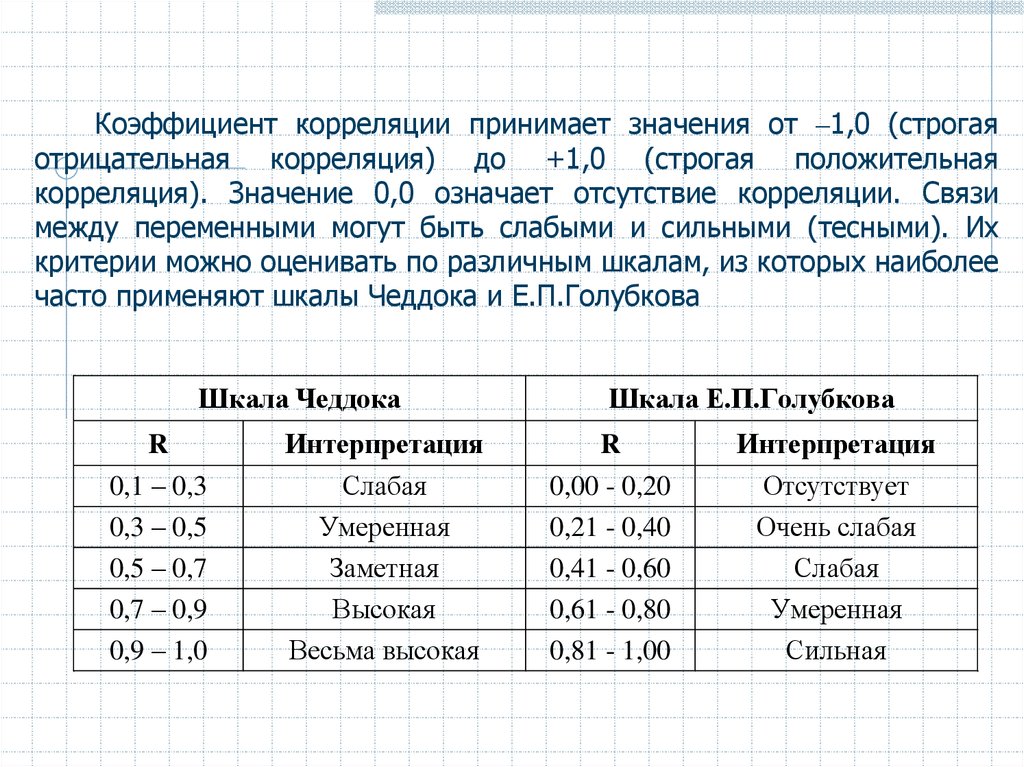
Коэффициент корреляции принимает значения от –1,0 (строгаяотрицательная корреляция) до +1,0 (строгая положительная
корреляция). Значение 0,0 означает отсутствие корреляции. Связи
между переменными могут быть слабыми и сильными (тесными). Их
критерии можно оценивать по различным шкалам, из которых наиболее
часто применяют шкалы Чеддока и Е.П.Голубкова
Шкала Чеддока
Шкала Е.П.Голубкова
R
Интерпретация
R
Интерпретация
0,1 – 0,3
0,3 – 0,5
0,5 – 0,7
0,7 – 0,9
0,9 – 1,0
Слабая
Умеренная
Заметная
Высокая
Весьма высокая
0,00 - 0,20
0,21 - 0,40
0,41 - 0,60
0,61 - 0,80
0,81 - 1,00
Отсутствует
Очень слабая
Слабая
Умеренная
Сильная
5.
n1
2
0
(
y
b
b
x
)
i
0
1 i
n(n 2) i 1
n
b 0
0
n xi2
i 1
n x xi
i 1
i 1
n
n
2
i
b j
b t P,n 1
j
n
2
b 0
1
n
n x xi
i 1
i 1
n
n
2
i
b j b j b j
2
6.
yi b0 b1 xi b2 xi2n
n
U ( yi b0 b1 xi b2 xi2 ) 2 min
i 1
2
i
i 1
n
n
n
i 1
i 1
i 1
nb0 b1 xi b2 xi2 yi
n
n
n
n
b0 xi b1 x b2 x yi xi
2
i
i 1
3
i
i 1
i 1
i 1
n
n
n
n
i 1
i 1
i 1
i 1
b0 xi2 b1 xi3 b2 xi4 yi xi2
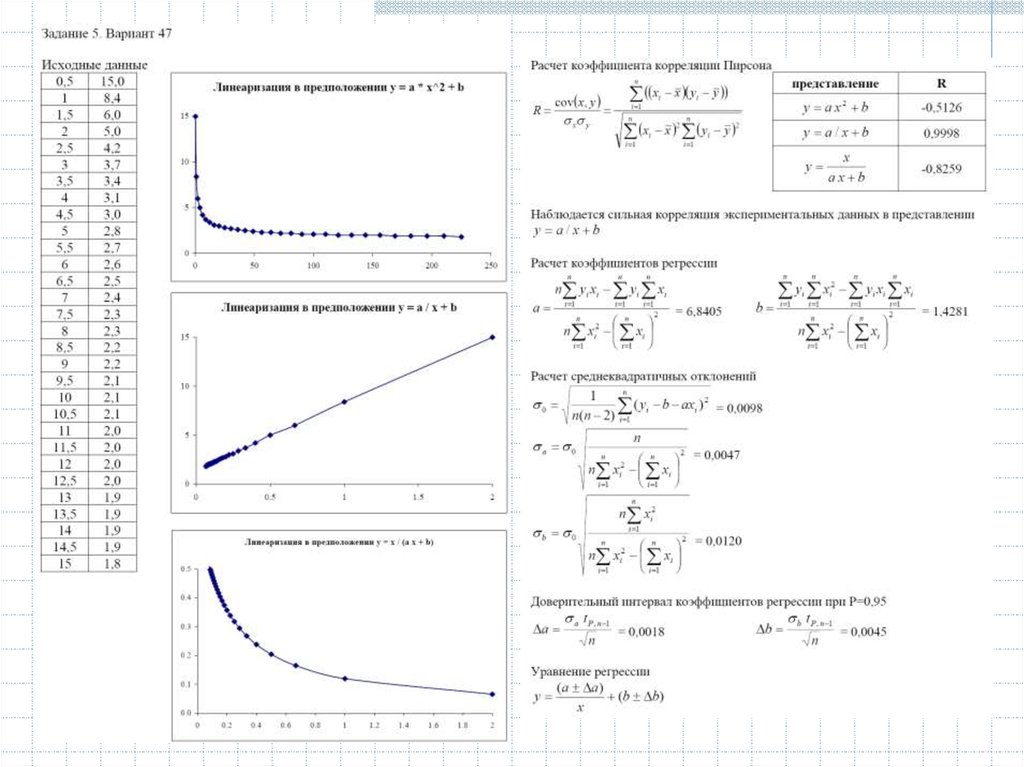
7. Линеаризация зависимостей
ku zЗамены
Вид зависимости
Ограничения
u
k
z
y ax 2 b
y
x2
a
b
a
y
b
Гипербола
x
y
1
x
a
b
x 0
y
ln x
a
b
ln y
x
ln a
ln b
ln y
ln x
a
ln b
ln y
x
a
ln b
ln y
1
x
a
ln b
x>0
y>0
a>0
b>0
y>0
x>0
b>0
y>0
b>0
y>0
b>0
1
y
1
x
a
b
Парабола второго (или высшего) порядка
Логарифмическая функция
Показательная функция
Степенная функция
y a ln x b
y ba x
y bx a
Экспоненциальная функция
y be ax
Экспоненциальная функция y be
x
y
ax b
b
y
x a
1
y
b ae x
a
x
y
1
y
xy
e-x
1
a
a
y 0
x 0
b
a
b
y 0
8.
U0 ~ 10 мВ9.
10.
11.
12.
13.
12
3
4
5
6
7
8
14.
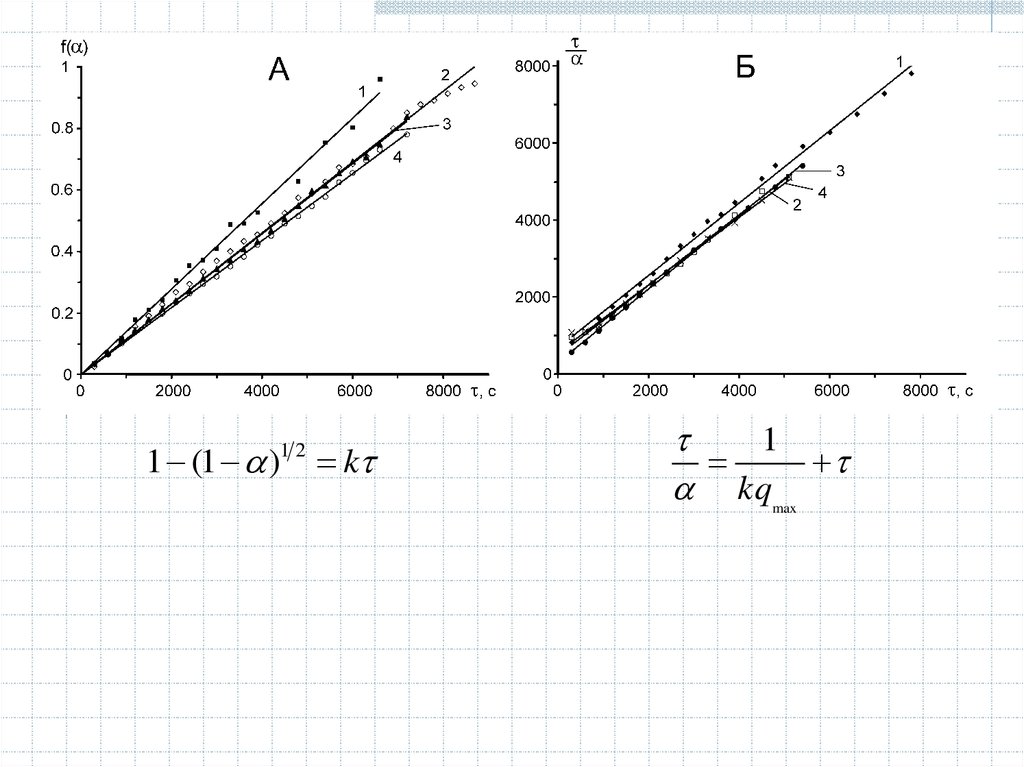
1 (1 )1 2 k1
kq
max







 Математика
Математика








