Похожие презентации:
Системы двух уравнений с двумя неизвестными
1. Системы двух уравнений с двумя неизвестными
2. Урок 1 Уравнения первой степени с двумя неизвестными. Системы уравнений
Цели: ввести понятие линейного уравнения сдвумя неизвестными, системы линейных
уравнений с двумя неизвестными;
способствовать усвоению определения решения
системы уравнений с двумя неизвестными.
3.
Уравнение и его свойстваОпределение
• Уравнение – это равенство, содержащее одну или несколько
переменных
ax=b
Коэффициенты
ax+by=c
а x + b y = c,
где а, b, c – заданные
числа.
Линейное уравнение с
одной переменной
Свободный член
Линейное
уравнение с
двумя
переменными
4. Из истории уравнений
• Уравнение с двумя неизвестнымивыражает зависимость между
двумя величинами , имеет
бесчисленное множество реше ний и является неопределенным.
• Решением таких уравнений
занимались в древности китайцы,
греки и индийцы.
• В «Арифметике» Диофанта
приведено много задач, решаемых
им с помощью неопределенных
уравнений.
Диофант из
Александрии
( 3 век )
5.
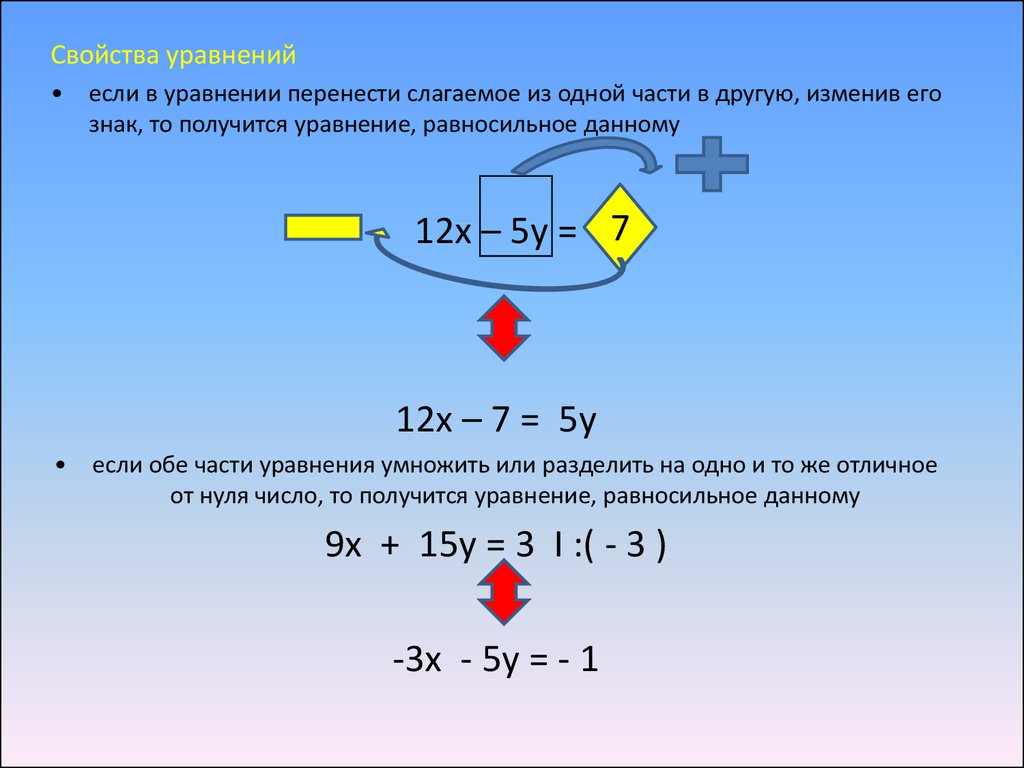
Свойства уравненийесли в уравнении перенести слагаемое из одной части в другую, изменив его
знак, то получится уравнение, равносильное данному
12х – 5у = 7
12х – 7 = 5у
если обе части уравнения умножить или разделить на одно и то же отличное
от нуля число, то получится уравнение, равносильное данному
9х + 15у = 3 Ι :( - 3 )
-3х - 5у = - 1
6. Задание 1.
1.1. Из линейногоуравнения с двумя
неизвестными
2х – 8у = - 10
выразите
переменную х:
2х = 8у – 10 Ι : 2,
Х = 4у - 5
1.2. Из линейного
уравнения с двумя
неизвестными
3х – 2у = 5 выразите
переменную у:
3х – 5 = 2у Ι : 2
3х - 5
=у
2
7. Решением уравнения с двумя неизвестными х и у называется упорядоченная пара чисел ( х ; у ), при подстановке которых в это уравнение получает
Решением уравнения с двумянеизвестными
х
и
у
называется упорядоченная пара
чисел ( х ; у ), при подстановке
которых в это уравнение
получается верное числовое
равенство.
8. Задание 2 Найдите все пары ( х ; у ) натуральных чисел, которые являются решениями уравнения.
• 2.1.13х + 4у =55
• 2.2.
5х + 7у =59
Ответ: ( 3 ; 4) Ответ: (2 ; 7)
(9 ; 2)
9.
Система уравнений и её решениеОпределение
Системой двух линейных уравнений с двумя неизвестными
называются два уравнения, объединенные фигурной скобкой.
Фигурная скобка означает, что эти уравнения должны быть
решены одновременно.
В общем виде систему двух линейных уравнений с
двумя неизвестными записывают так :
а1 х + b1 y = c1,
а2 х + b2 y = c2;
где
а , b , c а2 , b2 , c2
1
1
1,
10. Из истории систем уравнений
• Задачи на составление ирешение систем уравнений
встречаются в вавилонских
и египетских текстах II тысячелетия до н. э., в трудах
древнегреческих, китайских
и индийских ученых.
• Нижние индексы при буквах
Лейбниц
впервые употребил в 1675 г.
Готфрид Вильгельм
немецкий математик Лейбниц
( 1646 – 1716 )
11. Например, в системе а1 = 1, b1 = -1, с1 = 2; а2 = 3, b2 = -2, с2 = 9.
Например, в системех – у = 2,
3х – 2у = 9.
а1 = 1, b1 = -1, с1 = 2; а2 = 3, b2 = -2, с2 = 9.
Задание 3. (Устно.)
Проверьте, являются ли числа х = 4 , у = 3
решениями системы
2,5х – 3у = 1,
Решение:
5х – 6у = 2.
2,5 ·4 – 3 · 3 =1,
5·4 – 6 · 3 = 2.
Ответ: числа х = 4 , у = 3 являются решениями
системы
12. Решением системы уравнений с двумя переменными называется пара значений переменных, обращающая каждое уравнение системы в верное равенст
Решением системы уравнений сдвумя переменными называется
пара значений переменных,
обращающая каждое уравнение
системы в верное равенство
Решить систему уравнений это значит найти все её
решения или установить, что
их нет
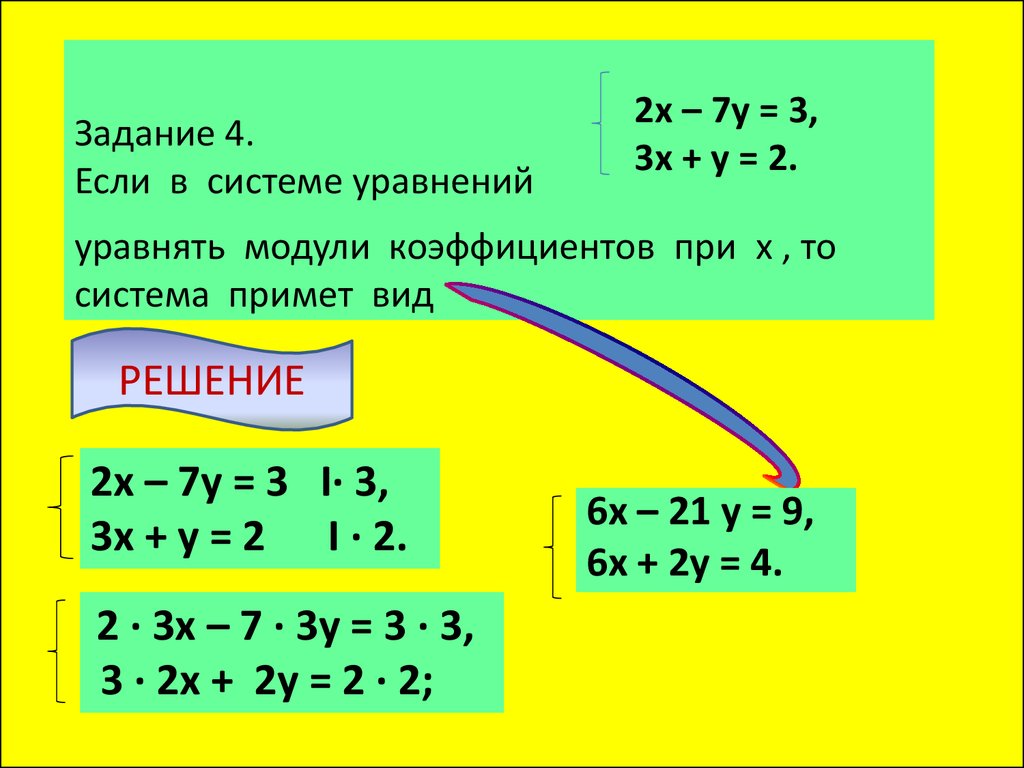
13. Задание 4. Если в системе уравнений
2х – 7у = 3,3х + у = 2.
уравнять модули коэффициентов при х , то
система примет вид
РЕШЕНИЕ
2х – 7у = 3 Ι· 3,
3х + у = 2 Ι · 2.
2 · 3х – 7 · 3у = 3 · 3,
3 · 2х + 2у = 2 · 2;
6х
6х –– 21
21 уу == 9,
9,
6х
6х ++ 2у
2у == 4.
4.
14. Домашнее задание
1. Учебник «Алгебра 7»,авторы Ш.А.Алимов и др. § 33
№ 615(1), 616(1), 617(1), 619(1).
2. Рабочая тетрадь по алгебре, 7,
авторы Ю.М.Колягин и др.
§ 33, № 3, 4(1), 5(1), 14(1).
3. Дополнительно: Дидактические материалы
«Алгебра 7», авторы М.В.Ткачева и др.
§ 33 ( стр. 90) № 4(1), 7.













 Математика
Математика








