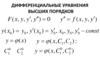Дифференциальные уравнения высших порядков. Уравнения, допускающие понижение порядка. Лeкция № 7-9

1. ЛEКЦИЯ № 7-9

Дифференциальные уравнения высших
порядков. Уравнения, допускающие понижение
порядка. Линейные дифференциальные
уравнения, однородные и неоднородные

2.

Дифференциальным уравнением n-го порядка называется уравнения
вида
F x, y, y , y , , y ( n) 0
или, если его можно разделить относительно старшей производной
y ( n) f x, y, y , y , , y ( n 1)
Решением уравнения n-го порядка является всякая n раз дифференцируемая
функция y = y(x), которая обращает это уравнение в тождество.
Задача Коши для уравнения n-го порядка состоит в том, чтобы найти
( n 1)
( n 1)
такое решение, которое удовлетворяет условиям y y0 , y y0 , y y 0
( n 1)
при x x0 , где x0 , y0 , y0 , , y0
- заданные числа, которые называются
начальными функциями или начальными условиями.
Общим решением дифференциального уравнения n-го порядка
называется функция
y x, C1 , C2 , Cn , зависящая от n произвольных
постоянных C1, C2 , Cn и такая, что:
1) она удовлетворяет уравнение при любых значениях постоянных C1 , C2 , Cn
2) при заданных начальных условиях
y x x y0 , y x x y0
, …., y (n 1) y0(n 1)
постоянные C1 , C2 , Cn
можно подобрать так, что функция y x, C1 Cn
будет удовлетворять этим условиям.
0
0

3. Дифференциальные уравнения, допускающие понижение порядка

Простейшими уравнением n-го порядка, допускающие понижение
порядка является уравнение вида: y ( n ) f ( x)
Решение такого уравнения находится n-кратным интегрированием, а
именно:
C x n 1 C x n 2
y f (x)dx
1
2
n 1 ! n 2 !
Cn 1x Cn
Пример. Найти общее решение уравнения : y 6 x 5
Решение. Интегрируя один раз получим:
Далее получим:
y 3x 2 5 x C1
5x 2
y x
C1 x C2
2
3
Окончательно:
x 4 5 x 3 C1 x 2
y
C2 x C3
4
6
2
Это и есть общее решение уравнения.

4.

Уравнение вида
y f x, y
не содержит явным образом искомой функции.
Для решения этого уравнения можно понизить порядок. Обозначим
y p
y p тогда
Подставим эти выражения в исходное уравнение получим уравнение
первого порядка
p f x, p
Проинтегрировав это уравнение получим:
Затем из формулыy p
p p x1 , C1
получим общий интеграл
y p x1 , C1 dx C2

5.

Пример. Решить дифференциальное уравнение
y
y
0
1 x
Решение. Подстановка y p , y p .
Тогда из данного уравнения второго порядка получим уравнение первого
порядка с разделяющимися переменными
,
Откуда
,
тогда
Так как
dp
p
dx 1 x
dp
dx
p 1 x
или
ln p ln 1 x ln C1
p C1 1 x
p y
dy
dx
, то
y C1 1 x
Интегрируя последнее уравнение , получаем общее решение исходного
уравнения:
x2
y С1 (1 x)dx C1 x C2
2

6.

Уравнение вида:
y f y, y
не содержит явным образом независимую переменную х.
Для его решения снова y dy p , но теперь мы будем считать p
dx
функцией от у. Тогда
2
y
d y dp dp dy
dp
p
dx 2 dx dу dx
dy
В результате получим уравнение первого порядка относительно
вспомогательной функции p(y)
dp
p
dy
f y, p
Решив это уравнение, найденную функцию p(y) подставим в исходную
подстановку. В результате получим уравнение
dy
p y1 , C1
dx
Интегрируя это уравнение, получаем общее решение
Ф x, y, C1 , C2 0

7.

Пример. Решить дифференциальное уравнение
1 у 2 у у
d2y
dp
dy
p
Решение. Сделаем замену y
, y
dx 2
dy
dx
рdp
dy
dp
2
Получим yp dy 1 р или 1 p 2 y
ln 1 p 2 ln y ln C1
Интегрируя это выражение, получим:
2
2
2
или
2
ln 1 p 2 ln y 2 ln C1
1 p C1 y 2
1
Возвращаясь к переменной y, получим
dy
2
или
,
C y2 1
dx
2
dy
2
1 C1 y 2
dx
1
Интегрируя, получим
dy
C1 y 1
2
2
dx
1
2
ln C1 y1 C1 y 2 1 x C2
C1

8. Линейные дифференциальные уравнения

Многие задачи математики, механики, электротехники и других
технических наук приводят к линейным дифференциальным уравнениям.
Уравнение вида a0 y a2 y a2 y f ( x)
, где a0 , a1 , a2 , функции от х
или постоянные числа, называется линейным дифференциальным уравнением
второго порядка.
a0 , a1 , a2 ,
называются коэффициентами уравнения , а функция f (x)
- его свободным членом.
Если свободный член равен нулю, т.е. f ( x) 0 , то уравнение называется
линейным однородным уравнением, в противном случае – линейным
неоднородным.

9. Линейные однородные дифференциальные уравнения с постоянными коэффициентами

Уравнение вида: ay by cy f x
где a, b, c постоянные , называются дифференциальными уравнениями
второго порядка с постоянными коэффициентами.
Рассмотрим линейное однородное дифференциальное уравнение вида
ay by cy 0
Это уравнение может быть приведено к виду
y py qу 0
Две функции у1 ( х) и у2 ( х) называются линейно независимыми
решениями линейного однородного уравнения, если их отношение отлично от
нуля, т.е. у1 ( х) 0
у2 ( х)
Теорема. Если y
1
иy
2
два линейно независимых решения уравнения ,
то
y C1 y2 C2 y2
есть его общее решение, где С1
и С2
- постоянные.

10.

Найдем решение уравнения
y py qу 0
Частные решения этого уравнения будем искать в виде
y ekx , где
k const
Тогда
y k ekx ,
y k 2 ekx
Подставляя
у, у и у в исходное уравнение, получим
ekx (k 2 pk q) 0
Так как
e kx 0
, то
k 2 pk q 0
Это уравнение называется характеристическим уравнением по отношению к
линейному однородному уравнению с постоянными коэффициентами.
При решении этого уравнения возможны три случая:
1) k1 и k2 действительные и различные числа. Тогда общее решение
уравнения будет иметь вид y C1ek1 x C2ek 2 x
2) k1 и k2 действительные равные корни. Тогда общее решение имеет вид
y e k1 x (C1 C2 x)
3) k и k комплексные корни: k1 i,
1
2
решение имеет вид:
y e x (С1 cos x С2 sin x)
k2 .iТогда общее

11.

Пример 1. Решить уравнение y 4 y 3 y 0 .
2
Составляем характеристическое уравнение k 4k 3 0
Его корни равны k1 1, k2 3 .
x
3x
Записываем общее решение: y c1e C2e
Пример 2. Решить уравнение y 25 y 0
Характеристическое уравнение имеет вид: k 2 25 0
Корни этого уравнения равны: k1 5i, k2 5i
Тогда общее решение примет вид:
y C1 cos 5x C2 sin 5x
Пример 3. Решить уравнение y 6 y 9 y 0
Характеристическое уравнение: k 2 6k 9 0
Находим корни этого уравнения: k k 3
1
2
Значит общее решение будет иметь вид
y e3 x (C1 C2 x)
.

12. Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами

Пусть дано неоднородное линейное дифференциальное уравнение
второго порядка
y py qy f (x)
Структура общего решения этого уравнения определяется следующей
теоремой:
Теорема. Общее решение неоднородного уравнения равно сумме
решения y0 однородного дифференциального уравнения y py qy 0 и
какого-нибудь частного решения y неоднородного уравнения, т.е.
y y0 y
Для нахождения частного решения используют два метода:
1) метод неопределенных коэффициентов;
2) метод вариации произвольной постоянной

13. Метод неопределенных коэффициентов

1) Пусть правая часть уравнения представляет собой произведение
показательной функции на многочлен:
f ( x) Bn ( x) e x ( B0 x n B1 x n 1 ... Bn )e x
где
Bn (x) -многочлен n-й степени.
Тогда возможны следующие случаи:
а) Число α не является корнем характеристического уравнения k 2 pk q 0
В этом случае частное решение нужно искать в виде
y Pn ( x) e x ( A0 xn A1xn 1 ... An )e x
б) Число α является однородным корнем характеристического уравнения. В
этом случае частное решение нужно искать в виде :
y x Pn ( x) e x
в) Число α есть двукратный корень характеристического уравнения. Тогда
частное решение следует искать в виде
y x2 Pn ( x) e x

14.

Пример 1. Решить уравнение y 5 y 6 y x
Решение. Найдем общее решение однородного дифференциального
уравнения y 5 y 6 y 0 . Составим характеристическое уравнение и
найдем его корни k 2 5k 6 0,
k1 1, k2 6
Общее решение однородного уравнения имеет вид y0 C1e x C2e 6 x
Так как в правой части 0 , то правую часть можно представить в виде
f ( x) x e0 x , причем 0 не является корнем характеристического уравнения,
поэтому частное решение будем искать в виде
y A0 x B , тогда y A, y 0
Подставляя эти выражения в исходное уравнение, получим
5 A0 6( A0 x B) x
Приравняв коэффициенты при одинаковых степенях x, получим
1
5
6 A0 1,
5 A0 6B 0
или A0 6 , B 36
1
5
Следовательно, частное решение примет вид
y x
Общее решение y y0 y получится в виде
y C1e x C2e 6 x
6
36
1
5
x
6
36

15.

x
Пример 2. Решить дифференциальное уравнение y 2 y y e
Решение. Найдем решения однородного уравнения y 2 y y 0 . Здесь
характеристическое уравнение имеет вид k 2 2k 1 0 . Его корни k1 k2 1 .
Общее решение однородного уравнения имеет вид
y0 (C1 C2 x) e x
1
является двукратным корнем характеристического уравнения, значит
частное решение уравнения имеет вид
2
x
y A(2 4 x x 2 ) e x
y Ax 2e x , тогда y A(2 x x ) e ,
Подставляя y, y , y в заданное дифференциальное уравнение, получим
A (2 4 x x 2 ) 2(2 x x 2 ) x 2 1
Откуда
2 A 1,
A
1
2
1
Следовательно, частное решение имеет вид y x 2e x
2
Общее решение уравнения равно
y (C1 C2 x) e x
1 2 x
xe
2

16.

2) Пусть правая часть уравнения имеет вид
f ( x) e x ( An ( x) cos x Bm ( x) sin x)
где An (x) и Bm (x) многочлены.
а) если i не является корнем характеристического уравнения,
то частное решения уравнения следует искать в виде
y e x ( Pn ( x) cos x Qm ( x) sin x)
где Pn (x) и Qm (x) - многочлены, степень которых равна наивысшими
степенями многочленов An (x) и Bm (x) .
б) Если i
есть корень характеристического уравнения, то
частное решение имеет вид
y x e x ( Pn ( x) cos x Qm ( x) sin x)

17.

Пример. Решить уравнение y 2 y 5 y 2 cos x
Решение. Корни характеристического уравнения k 2 2k 5 0
равны
k1 1 2i, k2 1 2i . Поэтому общий интеграл соответствующего однородного
уравнения y 2 y 5 y 0 является функция
y0 e x (C1 cos 2 x C2 sin 2 x)
Частное решение ищем в виде
y P cos x Q sin x
Тогда y P sin x Q cos x , y P cos x Q sin x , где P и Q постоянные
числа.
Подставляя y, y , y в данное уравнение, получим
4 P 2Q 2
и 2 P 4Q 0
2
1
Откуда
P , Q
5
Частное решение:
5
у
2
1
cos x sin x
5
5
Окончательно, общее решение примет вид
2
1
y e x (C1 cos 2 x C2 sin 2 x) cos x sin x
5
5